Классификация избыточных кодов

Общая классификация кодов приведена на рисунке 5.2.

Блочные коды характеризуются тем, что информационная последовательность единичных элементов разделяется на отдельные части, каждая из которых кодируется отдельно и независимо от других частей, образуя разрешенные слова избыточного кода.

Равномерные блочные коды характеризуются одинаковой длиной разрешенных кодовых слов, в отличие от неравномерных кодов.

В непрерывных кодах информационная последовательность единичных элементов не разделяется на части, а кодируется непрерывно, причем проверочные единичные элементы записываются на определенные позиции между информационными.

Равномерные блочные коды подразделяются на линейные и нелинейные. Линейные коды образуют наиболее обширный подкласс кодов и определяются тем, что сумма по модулю два двух и более разрешенных кодовых комбинации кода формирует комбинацию этого же кода. Нелинейные коды не обладают этим свойством. Примером не линейных кодов является код с постоянным весом, применяемый в телеграфии, а так же коды с естественной избыточностью. В некоторых случаях линейные коды называют групповыми, что обусловлено описанием подмножества разрешенных КК длины N как подгруппы, в которых информационные единичные элементы разделены и расположены на строго определенных позициях. Их называют систематическими, в отличие от несистематических кодов, в которых нельзя в явном виде выделить информационные и проверочные элементы. Систематические коды, как правило, обозначаются (n, k) -кодами.

Линейные систематические коды

Линейные систематические коды строятся путем добавления к каждой k‑значной комбинации первичного кода проверочных элементов, выбираемых по определенному правилу. Запишем кодовую комбинацию кода в виде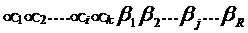

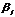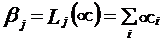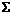В линейных кодах для определения проверочных элементов используются линейные формы, т.е. , где означает, что сложение производится по определенным правилам (для кодов с основанием 2 сложение осуществляется по модулю два).

Таким образом, для задания линейного систематического кода достаточно задать n линейных форм

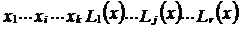где x_i - информационные элементы;

L_j(x) - линейная форма, с помощью которой находится j-й проверочный элемент.

Пример. Заданы линейные формы ,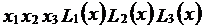

где .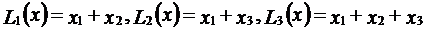

Определить 2³- I комбинаций линейного кода. Для вычисления комбинаций линейного кода составим таблицу.

Минимальное кодовое расстояние полученного кода d =3, т.е. он способен обнаруживать одиночные и двойные ошибки или исправлять только одиночные ошибки.

Построение с помощью порождающей матрицы

Зная закон построения кода, можно определить все множество разрешенных кодовых комбинаций и, расположив их друг над другом, получить матрицу содержащую n столбцов и (2³-1) строк (см. код в таблице).

Однако при больших значениях n и k такое описание кода оказывается громоздким, поэтому код записывается в более компактной форме. Это достигается путем выбора из всех строк матрицы только линейно независимых строк. Для рассмотренного кода это комбинации Х1, Х2, и Х4 .

Матрица G, содержащая только линейно независимые строки (комбинации) линейного кода, является порождающей (образующей, производящей).

Порождающей называется матрица, с помощью которой производится построение кода.

Например, комбинация Х3 является суммой по модулю два первой и второй строки матрицы G, а комбинация Х6 = Х2+Х4, т.е. второй и третьей строки матрицы и т.д.

В качестве линейно независимых могут быть выбраны любые k строк при записи порождающей матрицы. Однако более удобной является запись, соответствующая матрице G, когда первые k столбцов представляют собой единичную матрицу I с единицами по главной диагонали. Это так называемая каноническая форма порождающей матрицы.

Построение с помощью проверочной матрицы

Проверочной называется матрица, с помощью которой строится система проверок при обнаружении и исправлении ошибок.

Проверочная матрица Н содержит r строк и n столбцов (рисунок 6.1, б). В каждой строке проставляется I на позиции, соответствующей только одному проверочному разряду, а на информационных позициях I записывается для элементов, участвующих в формировании данного проверочного разряда.

Таким образом, проверочная матрица H получена в канонической форме, определяемой наличием на месте проверочных элементов единичной матрицы I размерности R .

Проверка принадлежности n-значной кодовой комбинации к множеству разрешенных комбинаций данного кода включает r этапов. На каждом этапе осуществляется суммирование по модулю 2 элементов проверяемой комбинации на тех позициях, на которых стоят единицы данной строки проверочной матрицы. Результат на всех этапах проверки должен быть равен нулю.

Введем обозначение кодовых комбинаций в виде векторов и используем известные правила сложения и перемножения матриц. Тогда n-значная кодовая комбинация может быть представлена в виде вектор-строки ,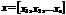

или вектор-столбца X t = X1

X2 .. Xn ,

где Xt - вектор-столбец, транспонированный к вектор-строке Х.

В этом случае проверка кодовой комбинации определяется уравнением

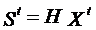, (6.1)

где 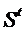- вектор-столбец синдрома (результатов проверки). Для разрешенных кодовых слов 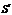=0, а для запрещенных .

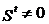Процедуры обнаружения ошибок

После того, как исходная кодовая комбинация закодирована в полное кодовое слово Х, оно передается по каналу, подвергающемуся действию помех. Канал накладывает на кодовое слово вектор помехи

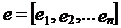где е_i = 0, если канал не искажает i-ый элемент;

е_i = 1, если канал искажает i-ый элемент.

Полученное слово описывается последовательностью

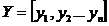где 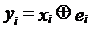или в векторной записи .

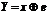Декодер начинает работу с вычисления синдрома, определяемого уравнением (6.1)

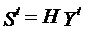Если 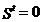, то ошибка либо отсутствует, либо не обнаруживается (т.е. одна разрешенная КК перешла в другую разрешенную под воздействием помехи). Если синдром 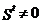,что свидетельствует о наличии ошибки, то принятое слово Y стирается.

Пример. Код определяется проверочной матрицей на рис.6.1,б), х=101100 и e=001000. Принятое слово: Y=x + e.

Вычисление синдрома приведено на рис.6.1,в). Ошибка обнаружена, так как .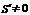

Рассмотренный метод декодирования с обнаружением ошибок называется синдромным. Возможен так же метод сопоставлений.

Дата добавления: 2018-05-12; просмотров: 618; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 Следующая ⇒

Мы поможем в написании ваших работ!