Строгая математическая индукции
При доказательствах некоторых высказываний о целых числах иногда требуется более строгая версия принципа индукции.
Принцип строгой индукции
Пусть S(n) – некоторое высказывание о целом числе n и требуется доказать, что S(n) справедливо для всех положительных n. Для этого необходимо:
1) доказать, что справедливо S(1);
2) доказать, что если справедливы S(1), S(2), S(3), ..., S(n) для всех положительных n, то справедливо и S(n + 1).
Отметим, что эта версия индукции почти идентична простой индукции, за одним исключением: при доказательстве второго положения в качестве гипотезы предполагается не просто справедливость высказывания S(n), а справедливость высказываний S(1), S(2), S(3), ..., S(n). Исходя из этой более строгой гипотезы, необходимо, как и выше, доказать справедливость S(n + 1).
Интуитивно ясно, что эти два положения подразумевают справедливость S(n) для любого положительного числа n. Из первого положения известно, что S(1) справедливо, а из второго следует, что если справедливо S(1), то справедливо и S(2). Так как S(1) действительно справедливо, следовательно, то же можно сказать и о S(2). Затем, так как и S(1), и S(2) справедливы, из второго положения следует справедливость S(3). Из справедливости высказываний S(1), S(2), S(3) и второго утверждения вытекает справедливость высказывания S(4) и т. д.
Рассмотрим несколько примеров, в которых полезно использовать принцип строгой индукции.
Пример 1.3. Простым числом называется положительное число, делящееся без остатка только на 1 и на само себя. Мы хотим доказать, что каждое положительное число n можно представить в виде произведения одного и более простых чисел. Докажем это с помощью строгой индукции по n:
|
|
|
1) если n = 1, то это число является простым, и, следовательно, его можно представить как «произведение» одного простого числа;
2) предположим, что каждое из чисел 1, 2, ..., n может быть записано в виде произведения простых чисел. Необходимо показать, что число n + 1 также можно представить в виде произведения простых чисел. Если n + 1 является простым числом, то очевидно, что его можно записать в виде произведения одного простого числа на 1. Если n + 1 – не простое число, тогда существует некоторое положительное число a, такое, что 1 < a < n + 1, и оно делит n + 1 без остатка.
Другими словами,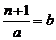 
, или n + 1 = a×b.
Каждое из чисел a и b меньше n. Следовательно, по гипотезе индукции и a, и b можно представить в виде произведения простых чисел. Отсюда очевидно, что и n + 1 можно записать как произведение этих же простых чисел, так как n + 1 = a×b.
Следует отметить, что в этом примере, по существу, требуется строгая индукция. О числах a и b известно лишь только то, что они меньше n. Поэтому, для того чтобы использовать индукцию, необходимо знать, что каждое из положительных чисел 1, 2, ... , n может быть представлено в виде произведения простых чисел. Одного предположения о том, что n можно записать в виде произведения простых чисел, оказывается недостаточно.
|
|
|
Пример 1.4. Рассмотрим последовательность чисел, называемых числами Фибоначчи. В нее входят f0 = 0, f1 = 1, f2 = 1, f3 = 2, f4 = 3, f5 = 5, f6 = 8, ... , где (n + 1)-е число Фибоначчи определяется как fn + 1= fn + fn – 1 (для n ³ 1). Пусть = (1 +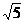 
)/2 и требуется доказать, что fn £ an – 1 для любого неотрицательного числа a. Для доказательства используем метод строгой индукции по n. Так как доказывается высказывание о неотрицательных числах, а принцип индукции сформулирован для положительных, используем модификацию метода:
1. Для n = 0 необходимо показать, что f0 £ a0 – 1 . Это справедливо, так как f0 = 0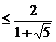 
= a–1. Необходимо рассмотреть особый случай, когда n = 1. Здесь мы имеем f1 = 1 £ 1=a0 = a1–1.
2. Предположим, что fm £ am – 1 справедливо для всех неотрицательных целых чисел m = 0, 1, 2, ... , n. Нужно показать, что fn+1 £ a(n + 1) – 1 также справедливо. По гипотезе индукции fn £ an – 1 и fn–1 £ a(n – 1) – 1. Поэтому
fn + 1 = fn + fn – 1 £an – 1 + an – 2 = an – 2 × (a+1).
|
|
|
Обратите внимание, что
a2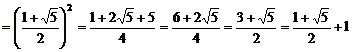 
= a + 1.
Фактически мы так и выбирали a, чтобы выполнялось условие a + 1 = a2. Поэтому мы получаем
fn + 1 = fn + fn – 1 £ an – 2 × (a+1) = an – 2 × a2 = an = a(n + 1) – 1 .
что и требовалось доказать.
Отметим, что необходимо было знать, что и fn, и fn–1 удовлетворяют гипотезе индукции. Только в этом случае доказательство возможно. Одного только знания о справедливости высказывания для fn недостаточно. Таким образом, строгая индукция нам необходима по существу. Отметим также, что в данном частном случае нам потребовалось доказывать, что f0 £ a0 и f1 £ a1; мы не можем записать f1 как f0 + f–1 , так как f–1 не существует.
В качестве упражнения по данной теме попробуйте изменить приведенный в данном разделе принцип индукции для доказательства справедливости высказывания S(n) для целых чисел n, удовлетворяющих условию n ³ n0, а не только для любых положительных целых чисел.
Дата добавления: 2018-05-12; просмотров: 395; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!