Энергетическая диаграмма, электромагнитный момент и механическая характеристика асинхронного двигателя

Электрические схемы АД с короткозамкнутым и фазным ротором представлены на рис.21.4 а, б, где внешняя окружность 1 – условное изображение цепи статора; окружность 2 – цепь ротора; две параллельные линии 3 – механическое соединение (вал); R_д – добавочный реостат, подключенный к цепи фазного ротора.

 Рис.21.4. Электрические схемы короткозамкнутого (а) и фазного асинхронных двигателей (б) и их
           диаграмма мощностей (в)

АД забирает из сети активную мощность P₁ = U_лI_лcosj. Часть этой мощности теряется в статоре в виде мощности P_R1 тепловых потерь в сопротивлениях R₁ обмотки статора и мощности P₀ тепловых потерь в сердечнике статора (за счет гистерезиса и вихревых токов). Вращающимся полем статора через воздушный зазор передается в ротор электромагнитная мощность      P_BI = P₁ – P_R1 – P₀ = MW₁,   

где М – вращающий электромагнитный момент двигателя; W₁ – угловая скорость поля статора.

Часть Р_F, полученной ротором, теряется в R₂ его обмотки. Оставшаяся часть преобразуется в механическую мощность

           Р_M = Р_BI – Р_R2 = МW,           

где W – угловая скорость ротора.

Потерями в сердечнике ротора можно пренебречь, поскольку в рабочем режиме частота токов в обмотке ротора мала (несколько герц). Вычтя из Р_M небольшую мощность механических потерь на трение и вентиляцию Р_FT, получим полезную механическую мощность Р₂ на валу АД. Мощность Р_ном (Р₂ в номинальном режиме) задается в паспорте. Суммарные потери в АД

           ΔР = Р₁ – Р₂ = Р_R1 + Р₀ + Р_R2 + Р_FT.   

КПД машины η = Р₂/Р₁ в номинальном режиме составляет 0,7 ¸ 0,9 для АД с Р_ном < 100 кВт, и 0,92¸0,96 для мощных машин.

Определим частоту f₂ ЭДС Е_2S, генерируемой полем статора в обмотке ротора. Поскольку поле статора вращается относительно ротора с угловой скоростью ΔΩ = Ω₁ – Ω = Ω₁s, то угловая частота ЭДС и токов ротора равна ω₂ = 2πf₂ = ΔΩр = Ω₁sр = 2πf₁s. Тогда частота токов ротора пропорциональна скольжению f₂ = sf₁, где f₁ – частота токов статора. Например, при питании АД от сети с частотой f₁ = 50 Гц при s_ном = 0,04 частота токов ротора в номинальном режиме составляет f_2ном = 2 Гц, а при пуске (s = 1) f_2п = f₁ = 50 Гц. Токи ротора, как и токи статора, образуют вращающееся магнитное поле ротора. Оба поля вращаются синхронно и образуют результирующее поле машины. Передача энергии из статора в ротор похожа на передачу энергии из первичной обмотки трансформатора во вторичную, но двигатель имеет воздушный зазор между статором и ротором. Вращающееся поле двигателя индуцирует в обмотках статора и ротора трансформаторные ЭДС: Е2 = 4,44f₁w₁K_об1Ф_m; Е_2s = 4,44f₂w₂K_об2Ф_m = sЕ₂,

где Е_2S = 4,44f₂w₂K_об2Ф_m – ЭДС неподвижного ротора; w₁, w₂ – числа витков статора и ротора (для короткозамкнутого ротора принимают w₂ = 0,5); K_об1, K_об2 – обмоточные коэффициенты, учитывающие снижение ЭДС из-за распределения обмоток по пазам, укорочения их шага и скоса пазов (для короткозамкнутого ротора K_об2 = 1).

В прикладных расчетах параметров двигателей коэффициент K_об принимают равным 0,95. Е₁ = 4,44f₁w₁K_об1Ф_m; Е_2s = 4,44f₂w₂K_об2Ф_m = sЕ₂,

где Е₂ = 4,44f₂w₂K_об2Ф_m – ЭДС неподвижного ротора; w₁, w₂ – числа витков статора и ротора (для короткозамкнутого ротора принимают w₂ = 0,5); K_об1, K_об2 – обмоточные коэффициенты, учитывающие снижение ЭДС из-за распределения обмоток по пазам, укорочения их шага и скоса пазов (для короткозамкнутого ротора K_об2 = 1).

В прикладных расчетах параметров двигателей коэффициент K_об принимают равным 0,95.

Выявим основные факторы, определяющие величину вращающегося электромагнитного момента М. С одной стороны, с учетом того, что R_2å = R₂ + R_д, суммарные потери в цепи ротора

Р_R2 = 3R_2åI₂².

С другой стороны –

Р_R2 = Р_BI – Р_F = МΩ₁ – МΩ = МΩ₁s.

Приравняв эти величины, находим

                     

Выражение позволяет определить пусковой I_2п и номинальный I_2ном токи ротора. Тогда момент на валу двигателя

           М = 3R_2å ,      

где R_2åI₂ – активная составляющая ЭДС Е_2s, равная Е_2scosj₂ (j₂ – сдвиг фаз между Е_2s и I₂).

Универсальная формула вращающего момента:

           М= С_МФ_mI₂cosj₂,              

где С_М = 3w₂K_об2p/ – константа.

Реактивное сопротивление цепи ротора Х_2s зависит от частоты f₂ и равно Х_2s= 2πf₂L₂ = 2πf₁sL₂ = sX₂, где Х₂= 2πf₁L₂, и L₂ – соответственно, индуктивное сопротивление и эквивалентное значение индуктивности неподвижного (заторможенного) ротора. Схема замещения на рис.21.5, а соответствует уравнению

.

 

Рис.21.5.Схемы замещения роторной цепи

 

Разделив обе части на s, получим уравнение

,

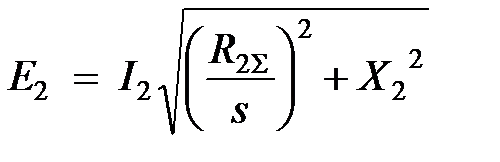которому соответствует цепь на рис. 27.6, б. В этой цепи ЭДС Е₂ имеет частоту f₁, т. е. цепь эквивалентна режиму заторможенного ротора. Мощность эквивалентного сопротивления R_2å/s равна электромагнитной мощности, поступающей в ротор:

.

Полная схема замещения АД аналогична Т-образной схеме замещения трансформатора, однако чаще пользуются упрощенной Г-образной схемой замещения одной фазы (рис.21.6), где R₁, X₁ – сопротивления статорной цепи; R, X – приведенные к статору сопротивления роторной цепи; R₀, X₀ – сопротивления ветви намагничивания; I₀ – ток холостого хода. Из-за воздушного зазора между статором и ротором ток холостого хода I₀ АД значительно выше тока холостого трансформатора и составляет (0,2¸0,5)I_1ном.

 Рис.21.6.Приведенная схема замещения АД

Зависимость частоты вращения от вращающего момента (n = f(M)) в установившемся режиме называют механической характеристикой двигателя.

Рис.21.7. Механическая характеристика АД

           Из схемы находим : . Подставив в формулу момента находим М:

                

               

 

 

где  Х_к – реактивное сопротивление при критическом моменте(X_К = X₁ + X).

Формула совместно с подстановкой s = 1 – определяет механическую характеристику АД. Связь s и n учитывают совмещением осей s и n. Механическая характеристика показана на рис.27.8 , где оси n и s направлены навстречу друг другу и n = 0 соответствует s = 1, а n = n₁ соответствует s = 0 (значения n указаны справа от оси, s – слева). Анализ формулы (3.40) с помощью dM/ds = 0 дает два экстремума:

           ;

               

где «+» соответствует двигательному режиму (квадрант I); «–» – генераторному (квадрант II). Скольжение s = s_Ки момент М = M_К = M_max называют критическими.

---

Дата добавления: 2018-05-12; просмотров: 510; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!