Точка пересечениямедиантреугольника есть центром тяжести треугольника.
Контрольная работа «Линейная алгебра и аналитическая геометрия»
Задание 1.
Вычислить определитель.
Решение:
Для удобства подсчета определителя выберем 1 столбец и разложим определитель по нем с помощью теоремы Лапласа:
Найдем каждыйминор по отдельности:
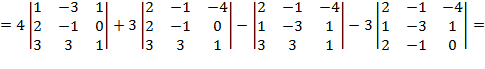
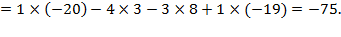
Тогда:
Задание 2.
Решить систему линейных уравнений тремя способами:
а) методом Гаусса;
б) по формулам Крамера;
в) с помощью обратной матрицы.
Решение:
По формулам Крамера:
а) Найдем определительосновнойматрицы:
= 
= 
, то заданая за теоремой Крамера СЛАУ иммеетединноерешение.
Найдем определители 
полученные из определителя , заменой соответствующего1-ого, 2-ого, 3-ого столбика столбиком свободных переменных :
= 
,
= 
,
= 
.
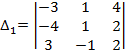За формулой Крамера:
Ответ: ( 
; 
; 
).
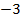Решение.
а) Випишемрасширенуюматрицу 
і сведем ее к треугольному виду:
Последний вид расширеннойматрицыимеет вид:
; 
Ответ: ( ; ; ).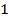
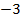А = 
; Х = 
; B= 
, тогда в матричной форме СЛАУ задаётся уравнением АХ = В. Определитель 
= 
, поэтому матрица А имеет обратную матрицу 
. Найдём :
Найдем алгебраическиедополнения 
к каждому елементу заданойматрици А :
, 
,
, 
,
, 
,
, 
,
.
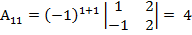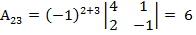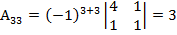Составимматрицуалгебраическихдополнений А* ( присоединенную к А):
.
Обратнаяматрица :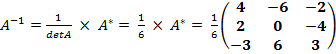 
.
|
|
|
За формулой: : Х = 
.
Ответ: ( ; ; ).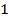
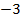Задание 3.
Решитьматричноеуравнение 
. Ответ проверить подстановкой в уравнение.
Решение:
Cведем наше уравнение к виду: 
. Для этого образуем матрицу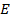 
путем решения уравнения: 
Теперь матричное уравнения запишется в виде: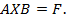 
Вычислим определитель матрицы А:
∆ = (-4)*4 - (-4)*1 = -12
Определитель матрицы А равен detA=-12
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1:Умножаем обе части этого равенства слева на A-1 и справа на B-1: A-1·A·X·B·B-1 = A-1·F·B-1. Так как A·A-1 = B·B-1 = E и E·X = X·E = X, то X = A-1·F·B-1.
Найдем обратную матрицу A-1.
Вычислим определитель матрицы B:
∆ = 0*(-5) - 4*5 = -20
Определитель матрицы B равен detB = - 20.
Найдем обратную матрицу B-1.
Матрицу X ищем по формуле: X = A-1·F·B-1
Проверим правильность уравнения:
Задание 4.
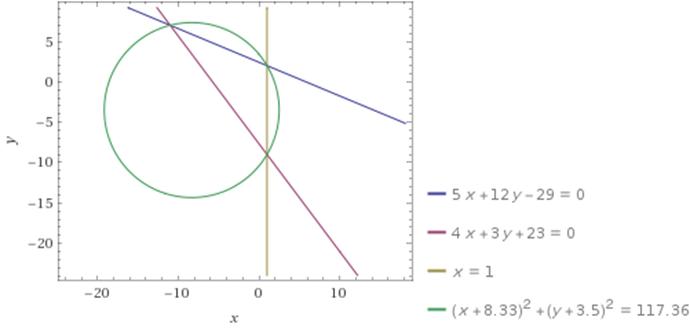
На плоскости даны точки 
Сделать чертеж
а) длину и уравнение ребра ВС (записать общее, каноническое, параметрические уравнения, а также уравнения в отрезках и с угловым коэффициентом, если это возможно);
б) косинус угла А;
в) уравнение прямой, проходящей через точку А параллельно стороне ВС;
г) высоту, проведенную к стороне ВС, и ее уравнение;
|
|
|
д) уравнение медианы, проведенной к стороне ВС;
е) координаты центра и радиус описанной окружности;
ж) площадь треугольника;
з) центр тяжести треугольника.
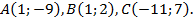
Решение:
а) Длину и уравнение ребра ВС (записать общее, каноническое, параметрические уравнения, а также уравнения в отрезках и с угловым коэффициентом, если это возможно):
Найдем вектор ВС:
= ( – 11 – 1 ;7–2 ) → = ( – 12; 5 ) .
Длина стороны ВС:
Уравнения прямой ВС:
Уравнение прямой, которой принадлежит сторона ВС: 
= 
, откуда:
, либо 12у + 5х – 29 = 0, либо 
, откуда угловой коэффициент прямой равен k =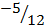 
.Уравнение в отрезках на осях:
б) Косинус угла А;
Найдем косинус угла А:
= 
, где 
координаты соответствующих нормальных векторов 
= 
= ( 0; 11) ; 
= 
= (–12; 16) .. Тогда:
в) Уравнение прямой, проходящей через точку А параллельно стороне ВС;
Уравнение прямой NA параллельной BC находится по формуле:
Подставляя 
, получим:
г) Высоту, проведенную к стороне ВС, и ее уравнение;
Составим уравнение высоты АD:
Прямая АD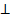 
ВС, поэтомувоспользуемсяуравнениемпрямой, котораяпроходит через точку А( 1 ; –9) перпендикулярно к вектору = ( 5 ;–12) . УравнениевысотыАDбудет :
5( х–1 ) –12 ( у +9 ) = 0 либо 12х–5у–57 = 0 .
|
|
|
д) Уравнение медианы, проведенной к стороне ВС;
Составим уравнение медианы АЕ:
Точка Е делит сторону ВС пополам, поэтому Е 
. Воспользуемся уравнением прямой, которая проходит через точки 
и 
:
, либо 4y+9х + 27 = 0.
е) Координаты центра и радиус описанной окружности;
Центр описанной окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.
Найдем уравнения прямых, на которых лежат стороны треугольника и их угловые коэффициенты:
Координаты середин сторон:
Угловые коэффициенты перпендикулярных прямых имеют обратную пропорциональность:
Уравнения серединных высот:
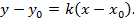
Решим систему:
Найдем длину, как расстояние от центра к любой из точек:
Найдем вектор АО:
= ( 1+ 8,33 ; –9+ 3,5 ) → = ( 9,33; – 5,5 ) .
Длина стороны ВС:
Тогда уравнение окружности:
ж) Площадь треугольника;
Найдем площадь треугольника:
Посчитаем площу грани 
:, какплощадьтреугольника 
, используя модуль векторного произведения векторов 
и 
:
SABC = S▲ABC = ½ 
.= 
= 
= 66.
з) Центр тяжести треугольника.
Точка пересечениямедиантреугольника есть центром тяжести треугольника.
Точка Е делит сторону ВС пополам, поэтому Е . Воспользуемся уравнением прямой, которая проходит через точки и :
|
|
|
, либо 4y+9х + 27 = 0.
Точка R делит сторону AС пополам, поэтому R 
. Воспользуемся уравнением прямой, которая проходит через точки 
и 
:
, либо 2y-х -3 = 0.
Решимсистему издвухуравнений:
В итоге, точка Q ( ;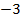 
) является центром тяжести треугольника.
Задание 5
Приведете уравнений кривой к каноническому виду и выполните чертеж.
| 7 | y = 2x2 + 4x + 3 | 9x2 -16 y2 - 54x - 64 y - 127 = 0 |
Решение:
Сведем уравнение к каноническому виду:
Получили уравнение параболы с центром в точке ( -1; 1) и параметром p = 0.25.
Сведем уравнение к каноническому виду:
Получили уравнение гиперболы с центром в точке ( 3; -2) и полуосями a = 4 и b = 3.
Задание 6.
В пространстве даны точки:
Сделать схематично чертеж пирамиды SABC и найти:
а) длину и уравнения ребра АВ;
б) площадь и уравнение грани АВС;
в) высоту, проведенную из вершины S к грани АВС, и ее уравнения;
г) проекцию вершины S на плоскость АВС;
д) уравнения проекции ребра АS на грань АВС;
е) уравнения прямой, проходящей через вершину S параллельно ребру АВ;
ж) уравнение плоскости, проходящей через вершину S параллельно грани АВС;
з) угол между ребрами АВ и AS;
и) угол между ребром AS и гранью АВС;
к) угол между гранями АВС и АВS;
л) координаты центра тяжести пирамиды АВСS;
м) объем пирамиды АВСS.
Решение:
а) Длину и уравнения ребра АВ;
Найдем кординатывекторов 
, 
, 
, :
= (3+2; 2+1 ; 1– 1 ) = ( 5 ; 3 ; 0 ) .
= (5+2; 2+1 ; 1– 1) = ( 7 ; 3 ; 0 ) .
= (1+2; – 1+1 ; 0– 1) = ( 3 ; 0 ; –1 ) .
Длинавекторов:
б) Площадь и уравнение грани АВС;
Найдем площадь грани с учётомгеометрическогосмысла векторного произведения:
Векторноепроизведение:
| | = |
S 
= S▲ = 
= 
= 
= 
= 
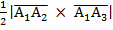= 3.
В уравнениеплоскости за тремя точками вставим координатыточек:
.
Имеем:
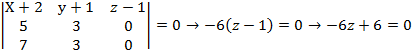– искомоеуравнениеплоскости.
в) Высоту, проведенную из вершины S к грани АВС, и ее уравнения;
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости ABC: - z + 1 = 0
е) Уравнения прямой, проходящей через вершину S параллельно ребру АВ;
ж) Уравнение плоскости, проходящей через вершину S параллельно грани АВС;
Плоскость, проходящая через точку M0(x0;y0;z0) и параллельнаяплоскостиAx + By + Cz + D = 0 имеетнаправляющий вектор (A;B;C) и, значит, представляетсяуравнением:
A(x-x0) + B(y-y0) + C(z-z0) = 0
Уравнениеплоскости ABC: - z + 1 = 0
0(x-1)+0(y-(-1))-1(z-0) = 0или0x+0y-z+0 = 0илиz = 0 .
з) Угол между ребрами АВ и AS;
Уголмежду векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:
Найдем уголмежду ребрами AB(5;3;0) и AS(3;0;-1):
γ = arccos(0.813) = 35.5630
и) Угол между ребром AS и гранью АВС;
Синус угламеждупрямой с направляющимикоэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле:
Уравнениеплоскости ABC: - z + 1 = 0, уравнениепрямой AS:
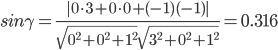
γ = sin(0.316) = 18.422o
к) Угол между гранями АВС и АВS;
Косинус угламеждуплоскостью A1x + B1y + C1 + D = 0 и плоскостью A2x + B2y + C2 +D = 0 равенуглумеждуихнормальными векторами N1(A1, B1, C1) и N2(A2, B2, C2):
Уравнениеплоскости ABC: - z + 1 = 0
Уравнениеплоскости ABD: -3x + 5y - 9z + 8 = 0
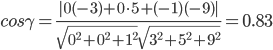
γ = cos(0.83) = 33.902o
м) Объем пирамиды АВСS.
Посчитаемобъемпирамиды, построенной на векторах 
, и , используя модуль произведения векторов:
Vпирамиды = 
= 
= 
( ед3) .
Дата добавления: 2018-05-12; просмотров: 154; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!