Підсумкова Тематична атестація №6
Марія Підручна
Збірник
контрольних робіт з геометрії
для поточного оцінювання і тематичного
контролю навчальних досягнень учнів
Клас
|
|
Тернопіль
«Підручники і посібники»
2008
УДК 371.26
П
Рецензент Ярослав Гап’юк — доцент кафедри математики і методики її викладання Тернопільського національного університету імені Володимира Гнатюка
Редактор Сергій Мартинюк
Літературний редактор Оксана Давидова
Обкладинка Світлани Демчак
Відповідальний за випуск Сергій Мартинюк
| Підручна Марія | |
| П | Збірник контрольних робіт з геометрії для поточного оцінювання і тематичного контролю навчальних досягнень учнів. 7 клас. — Тернопіль: Підручники і посібники, 2008. — ??? с. |
| ISBN |
Посібник містить завдання для контрольних робіт за усіма темами курсу геометрії 7 класу. Самостійні роботи містять завдання у 4 варіантах. Пропоновані роботи дозволяють здійснювати диференційований контроль навчальних досягнень учнів.
Для учителів математики та учнів загальноосвітніх шкіл.
УДК 371.26
ISBN
© Підручна М., 2008
Передмова
Посібник містить матеріал для проведення тематичної атестації учнів з курсу геометрії 7 класу. Матеріал для атестації з кожної теми поданий у чотирьох однакових за складністю варіантах. Завдання кожного варіанта згруповані по чотирьох рівнях складності, які, певною мірою, відповідають чотирьом рівням навчальних досягнень учнів: початковому, середньому, достатньому та високому.
|
|
|
У деяких варіантах є завдання «під рискою», які вчитель може використовувати як для атестації, так і для індивідуальної роботи з учнями.
Можна користуватися такими критеріями оцінювання атестаційних робіт.
Бал 3 учень отримує за виконання 6–7 завдань, бал 2 — за 5 завдань, бал 1 — за 4 завдання початкового рівня.
Виконання завдань середнього рівня оцінюється балами 4, 5, 6.
Завдання достатнього рівня включають у себе одне завдання на доведення теорем, що вивчаються в темі, оскільки досягнення учнем достатнього рівня передбачає вміння виконувати логічне обґрунтування тверджень у стандартних ситуаціях. Оцінюються завдання цього рівня балами 7, 8, 9.
Завдання високого рівня в основному посильні для більшості учнів, хоча окремі з них розраховані на школярів, які проявляють підвищений інтерес до вивчення математики. Оцінюються ці завдання балами 10, 11, 12.
Посібник може бути використаний і як дидактичний матеріал для самостійної роботи учнів з геометрії.
Тематична атестація №1.
Найпростіші геометричні фігури
та їх властивості
|
|
|
І Варіант
Початковий рівень
1. За рисунком вказати пряму, якій точка М належить, а точка K не належить.
а) NP; б) MP;
в)MK; г)NK.
2. За рисунком назвати промінь із початковою точкою В 
.
а) AM; б) AB;
в) ВD; г) CB.
3. За рисунком назвати відрізок, один кінець якого співпадає з точкою O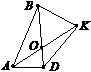 
.
а)BD; б)ОK;
в) AB; г)BK.
4. Порівняти відрізки (рис. до задачі 3) і поставити у квадратиках потрібний знак (<, >):
а)ВО ВD; б)АK ОK.
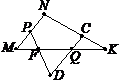5. Назвати трьома буквами кут з вершиною у точці М.
а) ÐMPD; б) ÐCKM;
в) ÐPDC; г) ÐNMK.
6. За рис. до задачі 5 назвати трьома буквами кут зі стороною DС.
а) ÐCDP; б) ÐCKQ; в) ÐDCN; г) ÐMNK.
7. Вказати правильне твердження 
.
|
|
|
а)ÐAOB > ÐAOC;
б)ÐAOC < ÐBOC;
в)ÐAOB < ÐAOC;
г)ÐAOB + ÐBOC = 180°.
8. Вказати правильне твердження 
.
а)AM > AN; б)AN = AM + MN;
в)AM = MN + MA; г)MN > AN.
9. Довжина відрізка АВ дорівнює 12 см. Точка K — його середина. Чому дорівнює довжина відрізка KВ?
а) 12 см; б) 24 см; в) 6 см; г) 3 см.
10. Промінь ОМ — бісектриса кута АОС, який дорівнює 60°. Як знайти кут АОМ 
?
а) 60° × 2; б) 60° : 2;
в) 90° – 60°; г) 180° – 60°.
Середній рівень
1. На відрізку АВ позначена точка М так, що АМ = 3 см, ВМ = 11 см. Чому дорівнює довжина відрізка АВ?
2. Промінь OC проходить між сторонами кута AOB. Знайти кут BOC, якщо ÐAOB = 65°, а ÐAOC = 30°.
3. На промені ОА позначена точка М. Яка з точок О, А, М лежить між двома іншими, якщо ОМ = 3 см, ОА = 7 см? Знайти довжину відрізка АМ.
4. Промінь ОМ — бісектриса кута АОВ. Кут АОМ дорівнює 54°. Знайти кут АОВ. 
Достатній рівень
1. Точка В належить відрізку АС. Відомо, що відрізок АВ на 3 см довший від відрізка ВС. Знайти довжини відрізків АВ і ВС, якщо АС = 31 см.
|
|
|
2. На деякій прямій відкладені відрізки АВ = 14 см і ВС = 8 см. Якою може бути довжина відрізка АС?
3. З вершини розгорнутого кута MON проведені в один бік два промені ОА і ОВ так, що ÐMОА = 30°, ÐBON = 60°. Знайти кут АОВ.
4. Промінь KC проходить між сторонами кута AKB. Кут AKC на 5° менший від кута BKC. Знайти ці кути, якщо ÐAKB = 105°.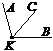 
Високий рівень
1. На прямій а послідовно задано точки А, В, С, D так, що АВ : ВС : СD =
= 1 : 2 : 5. Знайти довжини відрізків АВ, ВС, СD, якщо відрізок СD довший від відрізка ВС на 30 см.
2. Дано: MX = XN, MA = BN.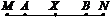 
Довести: AX = XB.
3. Промінь OK проходить між сторонами кута BOC. Знайти кути BOK і COK, якщо кут BOK у 6 разів більший від кута COK, а їх різниця дорівнює 100°.
4. Три точки M, N і K лежать на одній прямій. Відомо, що MN = 7 см, NK = 9 см. Яка з цих точок не може лежати між двома іншими?
ІІ Варіант
Початковий рівень
1. За рисунком назвати пряму, якій точка В належить, а точка А не належить 
.
а)DC; б) AD;
в)AB; г)ВC.
2. За рисунком назвати промінь із початковою точкою М 
.
а)KM; б)DP;
в)PM; г)MN.
3. За рисунком назвати відрізок, одним кінцем якого є точка D.
а) AB; б) DC;
в)AC; г)BА.
4. Порівняти відрізки (рис. до задачі 3) і поставити у квадратиках потрібний знак (>, <).
а)АD АС; б)АС DС.
5. Назвати трьома буквами кут з вершиною у точці N.
а) ÐCNM; б) ÐPMN;
в) ÐPKC; г) ÐNCD.
6. За рисунком назвати трьома буквами кут зі стороною OB.
а) ÐCOD; б) ÐCOB;
в) ÐABD; г) ÐBAD.
7. Вказати правильне твердження. 
а)ÐMON < ÐMOK;
б)ÐMON + ÐNOK = 180°;
в)ÐNOK > ÐMOK;
г)ÐMOK < ÐNOK.
| 8. Вказати правильне твердження. | 
|
а)ВС > АD; б)АD = АВ + ВС;
в)ВD = ВС + CD; г)AC < AB.
9. Довжина відрізка CD дорівнює 24 см. Точка A — його середина. Яка довжина відрізка АС?
а) 24 см; б) 48 см; в) 12 см; г) 6 см.
10. Промінь АВ — бісектриса кута МАN, який дорівнює 130°. Як знайти кут ВАN? 
а) 130° × 2; б) 180° – 130°;
в) 130° : 2; г) 130° – 90°.
Середній рівень
1. На відрізку MN позначена точка А так, що МА = 8 см. Чому дорівнює довжина відрізка АN, якщо MN = 17 см?
2. Промінь OС проходить між сторонами кута MON. Знайти градусну міру кута MOC, якщо ÐMON = 80°, а ÐCON = 55°.
3. На промені ОK позначена точка А. Яка з точок О, K, А лежить між двома іншими, якщо ОK = 9 см, ОА = 12 см? Знайти довжину відрізка АK.
4. Промінь ОА — бісектриса кута NOM. Знайти цей кут, якщо кут АОM дорівнює 10°.
Достатній рівень
1. Точка А належить відрізку CD. Відомо, що відрізок СА утричі довший від відрізка AD. Знайти довжини відрізків СА й AD, якщо CD = 24 см.
2. На деякій прямій відкладені відрізки АС = 9 см і СD = 15 см. Якою може бути довжина відрізка АD?
3. З вершини розгорнутого кута COD проведені в один бік два промені ОM і ОN так, що ÐCOM = 75°, ÐDON = 35°. Знайти кут MON.
4. Промінь OM проходить між сторонами кута AOB. Кут MOB на 20° більший від кута AOM. Знайти ці кути, якщо ÐAOB = 70°. 
Високий рівень
1. На прямій m послідовно позначені точки M, N, K, P так, що MN = 16 см, KP = 8 см, MP = 48 см. Знайти відстань між серединами відрізків MN і KР.
2. Дано: АD = СВ. Довести: АС = DВ.
3. Промінь OX проходить між сторонами кута AOB. Знайти кути AOX і BOX, якщо кут AOX у 5 разів більший від кута BOX, а їх різниця дорівнює 64°.
4. Три точки A, B, C лежать на одній прямій. Відомо, що AB = 9 см, BC = 4 см. Яка з цих точок не може лежати між двома іншими?
ІІІ Варіант
Початковий рівень
1. За рисунком назвати пряму, якій точка А належить, а точка В не належить 
.
а) ON; б)AC;
в) BC; г) AB.
2. За рисунком назвати промінь з початковою точкою N 
.
а) MN; б) KN;
в)NC; г) PN.
3. За рисунком назвати відрізок, один кінець якого є
точка М 
.
а) MC; б) CA;
в)CD; г)DА.
4. Порівняти відрізки (рис. до задачі 3) і поставити у квадратиках потрібний знак (>, <):
а)СМ АМ; б)AМ АC.
5. Назвати трьома буквами кут з вершиною у точці С.
а) ÐNAC; б) ÐACM;
в) ÐCAN; г) ÐDKC.
6. За рисунком до задачі 5 назвати трьома буквами кут, у якого стороною є промінь АK.
а) ÐANC; б) ÐMKC; в) ÐAKM; г) ÐNAK.
7. Вказати правильне твердження 
.
а)ÐАОС < ÐАОВ;
б)ÐВОС > ÐАОD;
в)ÐВОD = ÐВОС + ÐСОD;
г)ÐCOD > ÐBOD.
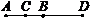8. Вказати правильне твердження.
а)АВ = АС + СВ; б)ВD > СD;
в)СD < СВ; г)AB = СВ.
9. Точка С — середина відрізка АВ. АС =8 см. Чому дорівнює довжина відрізка АВ?
а) 8 см; б) 16 см; в) 4 см; г) 32 см.
10. Промінь ВМ — бісектриса прямого кута АВС. Як знайти кут СВМ?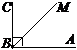 
а) 180° – 90°; б) 90° × 2;
в) 90° : 2; г) 180° – 45°.
Середній рівень
1. На відрізку АВ позначена точка М так, що МВ = 17 см. Чому дорівнює довжина відрізка АМ, якщо АВ = 32 см.
2. Промінь OM проходить між сторонами кута AOB. Знайти градусну міру кута BOM, якщо ÐAOB = 110°, ÐAOM = 85°.
3. На промені ОР позначена точка K. Яка з точок О, Р, K лежить між двома іншими, якщо ОР = 25 см, ОK = 13 см? Знайти довжину відрізка РK. 
4. Промінь OC — бісектриса кута AOB. Знайти градусну міру цього кута, якщо кут AOC дорівнює 42°. 
Достатній рівень
1. Точка М належить відрізку ВС, до того ж ВМ : МС = 2 : 3. Знайти довжини відрізків ВМ і МС, якщо ВС = 35 см.
2. На деякій прямій відкладені відрізки OD = 22 см і DC = 12 см. Якою може бути довжина відрізка OC?
3. З вершини розгорнутого кута AOC проведені в різні боки від ш два промені ОM і ОN так, що ÐAOM = 60°, ÐCON = 130°. Знайти кут MON.
4. Промінь ОА проходить між сторонами кута MOK. Кут MOA на 15° більший від кута AOK. Знайти ці кути, якщо ÐMOK = 85°.
Високий рівень
1. На прямій b послідовно позначені точки Х, Y, А, В так, що ХY = 10 см, YА = 30 см, ХВ = 52 см. Знайти відстань від середини відрізка YА до точки В.
2. Дано: ÐАОС = ÐDОВ. 
Довести: ÐАОВ = ÐDОС.
3. Промінь AX проходить між сторонами кута BAC. Знайти кути BAX і CAX, якщо кут BAX більший від кута CAX на 20°, а їх градусні міри відносяться як 5 : 3.
4. Три точки A, B, C лежать на одній прямій. Відомо, що AB = 11 см, BC = 13 см. Яка з цих точок не може лежати між двома іншими?
IV Варіант
Початковий рівень
1. За рисунком назвати пряму, яка проходить через точку С, але не проходить через точку А 
.
а) AD; б)BM;
в)AC; г)DС.
2. За рисунком назвати ппромінь з початковою точкою Р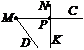 
.
а) MP; б) MC;
в) KP; г) PC.
3. За рисунком назвати відрізок, кінцем якого є точка D. 
а)AM; б) MС;
в)BD; г)BА.
4. Порівняти відрізки (рис. до задачі 3) і поставити у квадратиках потрібний знак (>, <)
а)АВ АD; б)АС МС.
5. За рисунком назвати трьома буквами кут з вершиною у точці М.
а) ÐMBC; б) ÐBMK;
в) ÐMKC; г) ÐAKC.
6. За рисунком назвати трьома буквами кут, у якого однією зі сторін є промінь MP.
а) ÐMDP; б) ÐMKP;
в) ÐNPM; г) ÐPMN.
7. Вказати правильне твердження 
.
а)ÐDОВ = 180°;
б)ÐАОС > ÐВОС;
в)ÐВОD = ÐВОА + ÐВОС;
г)ÐAOC < 180°.
8. Вказати правильне твердження.
а)MN = MK; б)NK > NP;
в)MP = MN + NK + KP; г)МP < NP.
9. Точка D — середина відрізка АС. DC = 4 см. Чому дорівнює довжина відрізка AC?
а)4 см; б) 2 см; в)8 см; г)1 см.
10. Промінь ОD — бісектриса розгорнутого кута АОС. Як знайти кут DОС?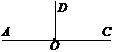 
а) 90° × 2; б) 180° : 2;
в) 90 : 2; г) 60°.
Середній рівень
1. На відрізку АВ завдовжки 15 см позначені точки M і N так, що АМ = 3 см, MN = 7 см. Знайти довжину відрізка NB.
2. Промінь OC проходить між сторонами розгорнутого кута AOA1. Знайти градусну міру кута A1OC, якщо ÐAOC = 40°.
3. На промені ОМ позначена точка С. Яка з точок О, М, С лежить між двома іншими, якщо ОМ = 10 см, а відрізок МС більший від відрізка ОМ на 5 см? Знайти довжину відрізка ОС. 
4. Промінь OB — бісектриса кута AOC. Знайти градусну міру цього кута, якщо кут BOC дорівнює 55°.
Достатній рівень
1. Точка М лежить на прямій АВ так, що точка В розміщена між точками А й М. Відрізок АВ становить п’яту частину відрізка ВМ. Знайти довжину відрізків АВ й ВМ, якщо АМ = 36 см.
2. На деякій прямій відкладені відрізки AC = 17 см і CK = 20 см. Якою може бути довжина відрізка AK?
3. З вершини розгорнутого кута MON проведені в різні боки від MN два промені ОA і ОB так, що ÐMOA = 50°, ÐNOB = 125°. Знайдіть кут AOB.
4. Промінь ОА проходить між сторонами кута MON. Кут MOA удвічі менший від кута AON. Знайти ці кути, якщо ÐMON = 66°.
Високий рівень
1. На прямій m послідовно відкладені відрізки АВ, ВС, СD, до того ж АВ : ВС = 1 : 3, СD = 50 см, АD = 90 см. Знайти довжини відрізків АВ і ВС.
2. Дано: ÐAOC = ÐBOM (див. рис.). Довести: ÐAOB = ÐCOM. 
3. Промінь OX проходить між сторонами кута AOB. Знайти кути AOX і BOX, якщо кут AOX менший від кута BOX на 15°, а їх градусні міри відносяться як 2 : 7.
4. Три точки M, N і K лежать на одній прямій. Відомо, що MN = 17 см, NK = 3 см. Яка з цих точок не може лежати між двома іншими?
Тематична атестація №2.
Суміжні й вертикальні кути
І Варіант
Початковий рівень
1. Два кути, які мають спільну сторону, а інші сторони цих кутів є доповняльними променями, називають...
а) вертикальними; б) суміжними;
в) гострими; г) тупими.
2. На якому з рисунків зображено суміжні кути?
| 
| 
| 
|
| а) | б) | в) | г) |
3. Сума суміжних кутів дорівнює...
а) 60°; б) 90°; в) 100°; г) 180°.
4. Як знайти кут, суміжний з кутом 50°?
а) 50° + 180°; б) 180° – 50°;
в) 20° + 50°; г) 90° – 50°.
5. Який кут буде вертикальний куту KАМ?
а) ÐNAP; б) ÐМАР;
в) ÐKАN; г) PAN.
6. Чому дорівнює кут, вертикальний куту 75°?
а) 37°; б) 150°; в) 25°; г) 75°.
7. За рисунком знайти градусну міру кута х.
а) 138°; б) 42°;
в) 69°; г) 150°.
8. Прямі АВ та СD перетинаються у точці О так, що ÐАОС = 45°. Як знайти кут ВОС?
а) 90° – 45°; б) 2 × 45°;
в) 180° – 45°; г) 100° + 45°.
9. Один із суміжних кутів на 20° менше від розгорнутого кута. Чому дорівнює цей кут?
а) 120°; б) 160°; в) 220°; г) 20°.
10. Яка з прямих перпендикулярна до прямої а?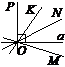 
а) OP; б) OK;
в) ON; г) OM.
Середній рівень
1. Чи можуть градусні міри суміжних кутів дорівнювати 21° і 158°?
2. Сума двох вертикальних кутів, які утворюються при перетині двох прямих, дорівнює 54°. Знайти ці кути.
3. Один з кутів, що утворюється при перетині двох прямих, дорівнює 25°. Знайти решту кутів.
Достатній рівень
1. Один із суміжних кутів на 20° більший від іншого. Знайти ці кути.
2. Кут СОВ, що утворюється при перетині прямих АВ і СD, дорівнює 130°. Промінь ОN — бісектриса кута АОD. Знайти градусну міру кута NОD. 
3. Знайти кут між бісектрисою кута в 50° і доповняльним променем до однієї зі сторін цього кута.
Високий рівень
1. Один з кутів, утворених при перетині двох прямих, у два рази менший від іншого. Знайти всі утворені кути.
2. Знайти суміжні кути, якщо бісектриса одного з них утворює зі стороною другого кут 140°.
3. Один із суміжних кутів утричі більший від різниці цих кутів. Знайти суміжні кути.
4. Дано: ОD^AB, ОF^OC. 
Довести: ÐFОD = ÐCОВ.
IІ Варіант
Початковий рівень
1. Кути АОВ і ВОС мають спільну сторону ОВ, а інші сторони ОА і ОС цих кутів є доповняльними променями. Такі кути називають... 
а) вертикальними; б) суміжними;
в) прямими; г) гострими.
2. На якому з рисунків зображено суміжні кути?
| 
| 
| 
|
| а) | б) | в) | г) |
3. Вказати правильне твердження 
.
а) ÐРОМ + ÐМОK = 180°;
б) ÐРОМ + ÐМОK = 90°;
в) ÐРОМ + ÐМОK = 100°;
г) ÐМОР > ÐKOP.
4. Як знайти кут, суміжний з кутом 68°?
а) 90° + 68°; б)180° + 68°; в)90° – 68°; г)180° – 68°.
5. Який кут буде вертикальним куту DОВ?
а) ÐВОА; б)ÐАОС;
в)ÐDОС; г) ÐАОD.
6. Знайти кут, вертикальний куту 120°.
а) 100°; б) 60°; в) 120°; г) 30°.
7. За рисунком знайти кут х.
а) 40°; б) 10°;
в) 160°; г) 20°.
8. Прямі АВ та СD перетинаються у точці О так, що ÐВОD = 105°. Як знайти ÐАОD? 
а) 180° – 105°; б) 105° : 2;
в) 105° – 90°; г) 90° + 105°.
9. Один із суміжних кутів на 30° менше від розгорнутого кута. Чому дорівнює цей кут?
а) 60°; б) 30°; в) 150°; г) 210°.
10. Кут МОВ дорівнює 90°. Чи будуть прямі NВ й АМ перпендикулярні?
а) Так;
б) ні;
в) не можна визначити.
Середній рівень
1. Чи може кут, суміжний з кутом 110°, дорівнювати 80°?
2. Сума двох вертикальних кутів, які утворюються при перетині двох прямих, дорівнює 40°. Знайти ці кути.
3. Один з кутів, що утворюється при перетині двох прямих, дорівнює 140°. Знайти решту кутів.
Достатній рівень
1. Один із суміжних кутів у 5 разів більший від іншого. Знайти ці кути.
2. Кут МОK, який утворюється при перетині двох прямих РK і NM, дорівнює 60°. Промінь ОА — бісектриса кута NOP. Знайти кут АОP. 
3. Знайти суміжні кути, якщо бісектриса одного з них
утворює з їх спільною стороною кут 25°.
Високий рівень
1. Один з кутів, утворених при перетині двох прямих, на 20° більший від іншого. Знайти всі утворені кути.
2. Знайти суміжні кути, якщо бісектриса одного з них утворює зі стороною іншого кут 91°.
3. Одна шоста частина одного із суміжних кутів і одна третя суміжного з ним кута в сумі дають 50°. Знайти ці кути.
4. Дано: ОС^FА, ОD^ОВ. Довести: ÐFОD = ÐСОВ.
IIІ Варіант
Початковий рівень
1. З вершини О розгорнутого кута АOA1 проведено промінь OC. Як називають кути AOC й A1OC?
а) Суміжними; б) вертикальними;
в) прямими; г) тупими.
2. На якому з рисунків зображено суміжні кути?
| 
| 
| 
|
| а) | б) | в) | г) |
3. Яке з тверджень правильне?
а) ÐBOC + ÐCOB1 = 90°;
б) ÐBOC + ÐCOB1 = 100°;
в) ÐBOC + ÐCOB1 = 180°;
г)ÐBOC – ÐCOB1 = 180°.
4. Як знайти кут, суміжний з кутом 110°?
а) 110° : 2; б) 180° – 110°; в)110° – 90°; г) 180° – 70°.
5. Назвати кут, вертикальний куту ВОD. 
а) ÐАОМ; б) ÐАOC;
в) ÐСОМ; г) ÐBOC.
6. Чому дорівнює кут, вертикальний куту 80°?
а) 80°; б) 40°; в) 160°; г) 100°.
7. За рисунком знайти кут х. 
а)30°; б)90°;
в)20°; г)60°.
8. Прямі MN і KР перетинаються у точці О так, що
ÐМОР = 70°. Як знайти ÐРОN? 
а)70° : 2; б)180° – 70°;
в)70° + 90°; г)70° · 2.
9. Один із суміжних кутів утричі менший від розгорнутого кута. Чому дорівнює цей кут?
а) 60°; б) 90°; в) 30°; г) 180°.
10. Прямі АВ і СD перпендикулярні. Чому дорівнює кут АОС?
а)100°; б)90°;
в)45°; г)180°.
Середній рівень
1. Чи може кут, суміжний з кутом 165°, дорівнювати 15°?
2. Сума двох вертикальних кутів, що утворюються при перетині двох прямих, дорівнює 36°. Знайти ці кути.
3. Один із кутів, що утворюється при перетині двох прямих, дорівнює 48°. Знайти решту кутів.
Достатній рівень
1. Знайти суміжні кути, якщо їх градусні міри відносяться як 2 : 3.
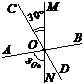2. За рисунком знайти градусну міру кута СОВ.
3. Знайти суміжні кути, якщо бісектриса одного з них утворює з їх спільною стороною кут 10°.
Високий рівень
1. Один з кутів, утворених при перетині двох прямих, на 50° менший від іншого. Знайти всі утворені кути.
2. Знайти суміжні кути, якщо бісектриса одного з них утворює зі стороною іншого кут 100°.
3. Третя частина одного із суміжних кутів дорівнює сьомій частині суміжного з ним кута. Знайти ці кути.
4. Дано: СО^MN, ÐDОС = ÐВON. 
Довести: ОD^ОВ.
ІV Варіант
Початковий рівень
1. Два кути називають суміжними, якщо у них...
а)одна сторона спільна;
б)одна сторона спільна, а дві інші сторони цих кутів є доповняльними променями;
в)дві сторони є доповняльними променями;
г)спільна вершина.
2. На якому з рисунків зображено суміжні кути?
| 
| 
| 
|
| а) | б) | в) | г) |
3. Сума суміжних кутів...
а) менша 180°; б)дорівнює 180°;в)дорівнює 90°; г) більша 180°.
4. Як знайти кут, суміжний з кутом 165°?
а)90° + 165°; б)180° + 165°; в)180° – 165°; г)165° – 90°.
5. Сторони кута B1AC1 є доповняльними променями сторін кута BAC. Такі кути називають... 
а)вертикальними; б)суміжними;
в)прямими; г)гострими.
6. Знайти кут, вертикальний куту 15°.
а)30°; б)115°; в)15°; г)165°.
7. За рисунком знайти кут х. 
а)80°; б)110°;
в)30°; г)50°.
8. Прямі MN і KP перетинаються у точці О так, що ÐKOM = 32°. Як знайти ÐKON? 
а)32°; б)180° – 32°;
в)90° + 32°; г)90° – 32°.
9. Суміжні кути рівні між собою. Чому дорівнює кожен з кутів?
а) 45°; б) 90°; в) 135°; г) 180°.
10. Вказати правильне твердження.
а)Прямі АВ і MN — перпендикулярні;
б)прямі СD і MN — перпендикулярні;
в)прямі АВ і CD — перпендикулярні;
г) ÐСON = 90°.
Середній рівень
1. Чи може кут, суміжний з кутом 31°, дорівнювати 159°?
2. Сума двох вертикальних кутів, що утворюються при перетині двох прямих, дорівнює 132°. Знайти ці кути.
3. Один із кутів, що утворюється при перетині двох прямих, дорівнює 150°. Знайти решту кутів.
Достатній рівень
1. Знайти суміжні кути, якщо один з них на 10° менший від іншого.
2. За рисунком знайти градусну міру кута АОС.
3. Знайти суміжні кути, якщо бісектриса одного з них утворює з їх спільною стороною кут 30°.
Високий рівень
1. Один із кутів, утворених при перетині двох прямих, у 5 разів менший від іншого. Знайти всі утворені кути.
2. Знайти суміжні кути, якщо бісектриса одного з них утворює зі стороною другого кут 130°.
3. Знайди суміжні кути, якщо один з них на 20° більший від різниці цих кутів.
4. Дано: СО^MN, ÐМОD = ÐСОВ. 
Довести: ОD^ОВ.
Тематична атестація №3.
Паралельні прямі. Трикутники.
Сума кутів трикутника
І Варіант
Початковий рівень
1. За рисунком вказати правильне твердження 
.
а) Ð3 і Ð6 — внутрішні різносторонні кути;
б) Ð1 і Ð5 — внутрішні односторонні кути;
в) Ð4 і Ð6 — відповідні кути;
г) Ð2 і Ð7 — внутрішні різносторонні кути.
2. Якої градусної міри має бути кут х, щоб прямі а і b були паралельними?
а) 105°; б) 150°;
в) 15°; г) 75°.
3. Дано: а||b, с — січна. Як знайти кут х?
а) 90° + 35°; б) 180° – 35°;
в) 90° – 35°; г) 180° + 35°.
4. У трикутнику KCD прилеглими кутами до сторони CD є:
а) ÐKCD, ÐKDC; б) ÐDCK, ÐDKC;
в) ÐCKD, ÐCDK. г) ÐKCD, ÐDCK.
5. Розгляньте рисунок. Сторона, яка лежить проти кута С трикутника, дорівнює...
а) 6 см; б) 7 см;
в) 8 см; г) 21 см.
6. Чи можуть сторони трикутника дорівнювати 3 см, 5 см і 8 см?
а) так; б) ні; в) не можна визначити.
7. ВМ — медіана трикутника АВС. Чому дорівнює відрізок МС, якщо АС = 18 см?
а) 18 см; б) 36 см;
в) 9 см; г) 6 см.
8. У трикутнику АСD ÐА = 60°, ÐD = 90°. Як знайти кут С?
а) 60° + 90°; б) 180° – (60° + 90°);
в) 180° + 60° + 90°; г) 180° – 60°.
9. Як знайти кут х? 
а) 85° – 30°; б) 180° – (85° – 30°);
в) 85° + 30°; г) 180° – 30°.
10. Вказати гіпотенузу трикутника ACD, у якого ÐD = 90°
а) AC; б) CD; в) AD; г) DC.
Середній рівень
1. Прямі а і b паралельні, пряма с — січна. Вказати правильну рівність.
а) Ð3 = Ð4; б) Ð1 = Ð5;
в) Ð2 = Ð8; г) Ð4 = Ð7.
2. Сума двох внутрішніх різносторонніх кутів при двох паралельних прямих і січній дорівнює 110°. Чому дорівнюють ці кути?
3. Один з гострих кутів прямокутного трикутника дорівнює 17°. Знайти інший гострий кут трикутника.
4. Периметр рівнобедреного трикутника дорівнює 36 см. Знайти його основу, якщо бічна сторона дорівнює 10 см.
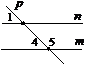5. Дано: m||n, p — січна, Ð1 = 45°. За рисунком знайти: Ð4, Ð5.
Достатній рівень
1. Дано: Ð3 = Ð2, Ð1 = 50°. Знайти: Ð2, Ð4.
2. Один з кутів трикутника дорівнює 65°, другий — на 35° більший від нього. Знайти кути трикутника.
3. Зовнішній кут трикутника дорівнює 120°. Знайти кути трикутника, не суміжні з ним, якщо один з цих кутів утричі більший від іншого.
4. Периметр трикутника дорівнює 18 см. Знайти його сторони, якщо вони відносяться 2 : 3 : 4.
5. Дано: а||b, с — січна. Кут 2 більший у 5 разів за кут 1. Знайти: Ð1, Ð2, Ð3.
Високий рівень
1. За рисунком знайти кут х.
2. Дано: m||n, p — січна, Ð1 + Ð4 = 220°. Знайти: Ð2, Ð3.
3. Знайти сторони рівнобедреного трикутника, якщо основа більша від бічної сторони на 2 см, а його периметр дорівнює 24 см.
4. Гострий кут прямокутного трикутника дорівнює 40°. Знайти кут між бісектрисою і висотою, проведеними з вершини прямого кута.
5. Кут між бічними сторонами рівнобедреного трикутника на 30° більший від кута при основі. Знайти кут, який утворює бісектриса кута при основі з основою.
6. У трикутнику АВС кут А дорівнює 50°, АС > АВ. На стороні АС відклали відрізок АD = АВ. Чи може кут АВС дорівнювати 64°?
IІ Варіант
Початковий рівень
1. За рисунком вказати правильне твердження.
а) Ð1 і Ð7 — внутрішні односторонні кути;
б) Ð4 і Ð5 — внутрішні різносторонні кути;
в) Ð3 і Ð7 — внутрішні односторонні кути;
г) Ð2 і Ð8 — відповідні кути.
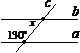2. Як знайти кут х, якщо прямі а та b — паралельні?
а) 180° – 130°; б) 90° + 130°;
в) 180° + 130°; г) 130° – 90°.
3. Дано: m||n, p — січна. Як знайти кут х?
а) 90° + 70°; б) 180° – 70°;
в) 70°; г) 90° – 70°.
4. Вказати кут трикутника MNK, який лежить між сторонами KN і KM.
а) ÐNMK; б) ÐMKN; в) ÐMNK; г) ÐCMA.
5. Розгляньте рисунок. Сторона, яка лежить проти кута D трикутника ACD, дорівнює...
а) 3 см; б) 15 см;
в) 13 см; г) 16 см,
6. Чи можуть сторони трикутника дорівнювати 5 см, 11 см і 15 см?
а) так; б) ні; в) не можна визначити.
7. CK — медіана трикутника CDM. Чому дорівнює відрізок MD, якщо DK = 6 см?
а) 6 см; б) 3 см;
в) 18 см; г) 12 см.
8. Два кути трикутника дорівнюють 30° і 80°. Як знайти третій кут?
а) 180°– (30° + 80°); б) 180° + 30° + 80°;
в) 30° + 80°; г) 80° – 30°.
9. Яка з рівностей правильна?
а) Ð4 = 60°; б) Ð4 = 50° + 70°;
в) Ð4 = 60° + 70°; г)Ð4 = 50° + 60°.
10. Вказати катети прямокутного трикутника AMD, у якого ÐА = 90°.
а) AM, MD; б) MD, DA; в) DA, AM; г) MA, AM.
Середній рівень
1. Прямі m і n паралельні, l — січна. Вказати правильну рівність.
а)Ð2 = Ð7; б)Ð1 = Ð7;
в)Ð3 = Ð8; г)Ð2 = Ð5.
2. Сума двох відповідних кутів при двох паралельних прямих і січній дорівнює 70°. Знайти ці кути.
3. За рисунком знайти кут х.
4. Периметр рівнобедреного трикутника дорівнює 42 см. Знайти його основу, якщо бічна сторона дорівнює 15 см.
5. Дано: а || b, с — січна. Ð1 = 100°. Знайти: Ð2, Ð3.
Достатній рівень
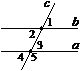1. Дано: Ð2 = Ð3, Ð2 = 64°. Знайти: Ð4, Ð5.
2. Один з кутів трикутника дорівнює 80°, інший у 4 рази менший від нього. Знайти третій кут трикутника.
3. За рисунком знайти кут х.
4. Знайти сторони трикутника, якщо його периметр дорівнює 26 см, а сторони пропорційні числам
4, 2, 7.
5. Дано: m||n, p — січна. Кут 1 менший від кута 3 на 20°. Знайти: Ð1, Ð2, Ð3.
Високий рівень
1. За рисунком знайти кут х.
2. Дано: а||b, с — січна, Ð1 + Ð3 = 90°. Знайти: Ð2, Ð4.
3. Знайти сторони рівнобедреного трикутника, якщо бічна сторона удвічі більша від основи, а периметр трикутника дорівнює 25 см.
4. Кут між бісектрисою і висотою, проведеними з вершини прямого кута трикутника, дорівнює 32°. Знайти гострий кут прямокутного трикутника.
5. Кут при основі рівнобедреного трикутника удвічі менший від кута між бічними сторонами. Знайти кут, який утворює бісектриса кута при основі з бічною стороною, що проходить через цю вершину.
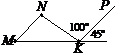6. Користуючись рисунком, знайти кути трикутника MNK, якщо MN||KP.
ІIІ Варіант
Початковий рівень
1. За рисунком вказати правильне твердження.
а) Ð1 і Ð7 — відповідні кути;
б) Ð2 і Ð6 — відповідні кути;
в) Ð1 і Ð8 — внутрішні різносторонні кути;
г) Ð4 і Ð5 — внутрішні односторонні кути.
2. Якої градусної міри має бути кут х, щоб прямі а та b були паралельні?
а) 180° – 120°; б) 120° – 90°;
в) 120° : 2; г) 120°.
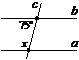3. Дано: а || b, с — січна. Як знайти кут х?
а) 180° – 75°; б) 75°;
в) 90° – 75°; г) 90° + 75°.
4. У трикутнику ABD кути BAD і BDA є прилеглими до сторони...
а) AB; б) BD; в) BA; г) AD.
5. Розгляньте рисунок. Сторона, яка лежить проти кута М трикутника MNK, дорівнює...
а) 10 см; б) 12 см;
в) 18 см; г) 40 см.
6. Чи можуть сторони трикутника дорівнювати 7 см, 4 см і 11 см?
а) так; б) ні; в) не можна визначити.
7. AD — бісектриса трикутника АВС. Чому дорівнює ÐВАС трикутника, якщо ÐDAC=20°?
а) 20°; б) 40°;
в) 10°; г) 80°.
8. Два кути трикутника дорівнюють по 50°. Як знайти третій кут?
а) 50 × 2; б) 180° – 50°;
в) 180° – (50° + 50°); г) 50° : 2.
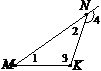9. Яка з рівностей правильна (див. рис.)?
а) Ð4 = Ð2 + Ð3; б) Ð4 = Ð1 + Ð3;
в) Ð4 = Ð1 + Ð2; г) Ð4 = Ð3.
10. Вказати гіпотенузу прямокутного трикутника CKD, у якого ÐK=90°.
а) CK; б) KD; в) DC; г) KC.
Середній рівень
1. Прямі m і n паралельні, p — січна. Вказати правильну рівність.
а) Ð7 = Ð3; б) Ð2 = Ð8;
в) Ð3 + Ð6 = 180°; г) Ð1 = Ð6.
2. Сума двох внутрішніх різносторонніх кутів при двох паралельних прямих і січній дорівнює 140°. Знайти ці кути.
3. Один з гострих кутів прямокутного трикутника дорівнює 45°. Чому дорівнює інший гострий кут трикутника?
4. Периметр рівнобедреного трикутника дорівнює 60 см. Знайти бічну сторону, якщо основа трикутника дорівнює 10 см.
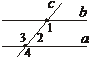
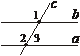5. Дано: а||b, с — січна. Ð1 = 120°. Знайти: Ð2, Ð3.
Достатній рівень
1. Дано: Ð1 + Ð2 = 180°; Ð3 = 130°. Знайти: Ð2, Ð4.
2. Один з кутів трикутника дорівнює 72°, інший на 15° менший від нього. Знайти третій кут трикутника.
3. За рисунком знайти кут х.
4. Периметр трикутника дорівнює 64 см. Одна сторона дорівнює 20 см, а дві інші сторони пропорційні числам 4 і 7. Знайти сторони трикутника.
5. Дано m||n, p — січна. Кут 1 більший на 30° від кута 3. Знайти: Ð1, Ð2, Ð3.
Високий рівень
1. За рисунком знайти кут х.
2. Дано: Ð1 + Ð4 = 180°, Ð2 = 100°. Знайти: Ð3, Ð4.
3. Знайти периметр рівнобедреного трикутника, якщо бічна сторона утричі більша від основи, а їх різниця дорівнює 16 см.
4. Гострий кут прямокутного трикутника дорівнює 65°. Знайти кут між бісектрисою і висотою, проведеними з вершини прямого кута.
5. Кут між бічними сторонами рівнобедреного трикутника відноситься до кута при основі як 3 : 1. Знайти кут, який утворює бісектриса, проведена до основи, з бічною стороною.
6. Довести, що бісектриси внутрішніх односторонніх кутів, що утворюються при перетині двох паралельних прямих третьою, перетинаються під прямим кутом.
ІV Варіант
Початковий рівень
1. Вказати правильне твердження.
а) Ð1 і Ð4 — внутрішні різносторонні кути;
б) Ð3 і Ð5 — відповідні кути;
в) Ð2 і Ð6 — відповідні кути;
г) Ð7 і Ð8 — внутрішні різносторонні кути.
2. Через вершину М трикутника АMВ проведено пряму MN, паралельну прямій АВ. За рисунком знайти кут В трикутника.
а) 60°; б) 120°;
в) 30°; г) 50°.
3. Дано: m||n, p — січна. Як знайти кут х?
а) 108°; б) 90° + 108°;
в) 108° – 90°; г) 180° – 108°.
4. Кут В трикутника CBD лежить між сторонами...
а) CB і CD; б) BC і BD;
в) DC і DB; г) CB і BA.
5. Розгляньте рисунок. Вкажіть кут, який лежить проти сторони, що дорівнює 10 см.
а) ÐN; б) ÐMNK;
в) ÐNKM; г) ÐM.
6. Чи можуть сторони трикутника дорівнювати 5 см, 13 см і 10 см?
а) так; б) ні; в) не можна визначити.
7. Два кути трикутника дорівнюють 40° і 130°. Як знайти третій кут трикутника?
а) 180° – (40° + 130°); б) 180° – (130° – 40°);
в) 40° + 130°; г) 130° – 40°.
8. Вказати правильне твердження. Зовнішній кут трикутника АСВ при вершині С — це кут...
а) ÐМСN; б) ÐАСB;
в) ÐВСN; г ÐNAB.
9. Сума яких кутів трикутника дорівнює 100°?
а) ÐА + ÐВ; б) ÐВ + ÐС;
в) ÐА + ÐС; г) ÐC + ÐBCM.
10. Вказати катети прямокутного трикутника ABD, у якого ÐА = 90°.
а) BA і BD; б) AB і AD; в) DA і DB; г) BD і DB.
Середній рівень
1. Прямі а та b паралельні, пряма с — січна. Вказати правильну рівність.
а) Ð3 = Ð5; б) Ð1+Ð8 = 180°;
в) Ð4 + Ð6 = 180°; г) Ð5 = Ð6.
2. Сума двох відповідних кутів при двох паралельних прямих і січній дорівнює 60°. Знайти ці кути.
3. За рисунком знайти кут х.
4. Периметр рівнобедреного трикутника дорівнює 48 см. Знайти бічну сторону, якщо основа трикутника дорівнює 20 см.
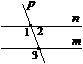5. Дано m||n, с — січна. Ð3 = 110°. Знайти: Ð1, Ð2.
Достатній рівень
1. Дано: Ð1 + Ð2 = 180°, Ð3 = 50°. Знайти: Ð2, Ð4.
2. Один з кутів трикутника дорівнює 17°, інший удвічі
більший від нього. Знайти третій кут трикутника.
3. Зовнішній кут трикутника дорівнює 80°. Знайти кути трикутника, не суміжні з ним, якщо один з цих кутів на 10° більший від іншого.
4. Периметр трикутника дорівнює 27 см. Знайти його сторони, якщо вони відносяться як 3 : 2 : 4.
5. Дано: m||n, p — січна. Кут 2 учетверо менший від кута 4. Знайти: Ð1, Ð2, Ð4.
Високий рівень
1. Один кут трикутника дорівнює 15°, а різниця двох інших кутів дорівнює 75°. Знайти невідомі кути трикутника.
2. За рисунком знайти кут х.
3. Знайти сторони рівнобедреного трикутника, якщо бічна сторона більша від основи на 3 см, а периметр трикутника дорівнює 36 см.
4. Кут між висотою і бісектрисою, проведеними з вершини прямого кута трикутника, дорівнює 35°. Знайти гострі кути прямокутного трикутника.
5. Кут при основі рівнобедреного трикутника в 4 рази більший від кута між бічними сторонами. Знайти кут, який утворює бісектриса кута при основі з основою.
6. Якщо гострі кути прямокутного трикутника відносяться як 1 : 3, то бісектриса прямого кута дорівнює одному з катетів. Довести це.
Тематична атестація №4.
Ознаки рівності трикутників
І Варіант
Початковий рівень
1. Два трикутники називають рівними, якщо в них...
а) сторони рівні;
б)відповідні сторони пропорційні;
в) відповідні кути рівні;
г) відповідні сторони і відповідні кути рівні.
2. Дано: DАВС = DА1В1С1. Вказати правильну рівність.
а) ÐА = ÐА1; б) ÐАСВ = ÐАВ1С;
в) АС = В1С1; г) ВС = А1В1.
3. Ознака рівності трикутників (за двома сторонами і кутом між ними).
Два трикутники будуть рівними, якщо...
а) дві сторони одного трикутника дорівнюють двом сторонам іншого трикутника;
б) два кути одного трикутника дорівнюють двом кутам іншого трикутника;
в) дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними іншого трикутника;
г)сторона і кут одного трикутника дорівнюють відповідно стороні та куту іншого трикутника.
4. Трикутники ACB і KMD рівні. Відповідними до сторони АС і кута D є:
а) MD; ÐC; б) MK; ÐA; в) KD; ÐB; г) MK; ÐB.
5. Дано: DMNK і DM1N1K1, MN = 9 см. M1N1 = 9 см, ÐN = 17°, ÐN1 = 17°, ÐМ = 85°. Щоб трикутник МNK дорівнював трикутнику M1N1K1, потрібно, щоб ÐM1 дорівнював:
а) 17°; б) 85°; в) 103°; г) 68°.
6. Трикутник MNK — рівнобедрений з основою MN. Вказати правильну рівність. 
а) МK = MN; б) МK = KN;
в) ÐK = ÐN; г) ÐM = ÐK.
7. Трикутник MNK дорівнює трикутнику M1N1K1, MN = 8 см, NK = 9 см, МK = 11 см. Знайти сторони М1N1, N1K1, М1K1 трикутника M1N1K1.
а) 8 см, 11 см і 10 см; б) 9 см, 9 см, 8 см;
в) 18 см, 9 см, 11 см; г) 8 см, 9 см, 11 см.
| 8. За рисунками вказати позначення медіани трикутника АВС. а) BN; б) AM; в) CK; г) NM. |  
|
9. Трикутник AMB — рівнобедрений з основою АВ. MD — бісектриса, проведена до основи. Чому дорівнює відрізок AD, якщо АВ = 8 см?
а) 16 см; б) 8 см; в) 4 см; г) 6 см.
| 10. Знайти довжину гіпотенузи МK трикутника MNK (див. рис.). а) 4 см; б) 8 см; в) 16 см; г) 30°. |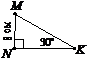 
|
Середній рівень
1. За рисунком знайти градусну міру кута Р та довжину відрізка МK. 
2. У трикутнику MNK: MN = 15 см, NK = 10 см. Знайти довжину сторони МK, якщо периметр трикутника дорівнює 36 см.
3. Точка О — середина відрізка МK. За рисунком довести, що трикутник ОМN дорівнює трикутнику ОKР.
4. Чи буде трикутник АВС рівнобедреним (див. рис.)? Пояснити.
Достатній рівень
1. Відрізки МK і NP перетинаються в точці О. MO = OP, ÐAMN = ÐBPK. Довести, що відрізок NO дорівнює відрізку ОK. 
2. Дано: DMKN = DАВС, МK = 12 см. ВС = 15 см. Сторона MN утричі менша від сторони KN. Знайти периметр трикутника АВС.
3. У трикутнику АВС проведена медіана СK. Сторона АС = 8 см, а СВ — більша від неї на 2 см. Знайти довжину відрізка АK, якщо периметр трикутника дорівнює 30 см. 
4. Довести рівність прямокутного трикутника за катетом і гіпотенузою.
5. Знайти кути рівнобедреного трикутника, якщо один з них на 20° більше від іншого (розглянути два випадки).
Високий рівень
1. Промінь АС — бісектриса кута ВАD, кут ВСK дорівнює куту DСK. Довести, що ВС = DС.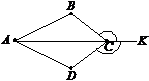 
2. Трикутник АВС дорівнює трикутнику А1В1С1. Сторона ВС удвічі менша від сторони A1В1, а сторона А1С1 на 7 см більша від сторони АВ. Знайти сторони трикутника АВС, якщо периметр трикутника А1В1С1 дорівнює 107 см.
3. Дано: Ð1 = Ð2, АK = NC (див. рис.). 
Довести: DKВN — рівнобедрений.
4. У рівнобедреному трикутнику АВС з основою АС проведена висота ВK. Периметр трикутника АВK дорівнює 15 см, а периметр трикутника АВС дорівнює 24 см. Знайти довжину висоти ВK.
5. Довести рівність прямокутних трикутників за катетом і медіаною, проведеною до цього катета.
ІІ Варіант
Початковий рівень
1. Якщо два трикутники рівні, то в них...
а) відповідні сторони рівні, а відповідні кути не рівні;
б) відповідні кути рівні, а відповідні сторони не рівні;
в) відповідні сторони і відповідні кути рівні;
г)усі кути рівні.
2. Дано: DMNK = DM1N1K1. Вказати правильну рівність.
а) МK = М1K1; б) ÐN = ÐK1;
в) ÐKMN = ÐK1N1M1; г) NK = M1N1.
3. Ознака рівності трикутників (за стороною і прилеглими до неї кутами).
Два трикутники будуть рівними, якщо...
а) два кути одного трикутника дорівнюють відповідно двом кутам іншого трикутника;
б) сторона і прилеглий до неї кут одного трикутника дорівнюють відповідно стороні і прилеглому до неї куту іншого трикутника;
в) сторона і два прилеглих до неї кути одного трикутника дорівнюють відповідно стороні і двом прилеглим до неї кутам іншого трикутника;
г)три кути одного трикутника дорівнюють трьом кутам іншого трикутника.
4. Трикутники XYZ і ABC рівні. Відповідними до сторони XY і кута Z є...
а) CA; ÐA; б) AC; ÐB; в) BC; ÐA; г) AB; ÐC.
5. Трикутник АВС дорівнює трикутнику MNK, MN = 18 см, NK = 19 см, МK = 21 см. Знайти сторони АВ, ВС, АС трикутника АВС.
а) 19 см, 19 см, 18 см; б) 18 см, 19 см, 21 см;
в) 21 см, 10 см, 19 см; г) 18 см, 19 см, 37 см.
6. Трикутник MNK — рівнобедрений з основою МK. Вказати правильну рівність. 
а) ÐМ = ÐK; б) ÐМ = ÐN;
в) ÐN = ÐK; г) MN = МK.
| 7. За рисунками вказати позначення висоти трикутника АВС. а) CC1; б) AK; в) BN; г) BB1. |  
|
8. Трикутники МKР і М1K1Р1 рівні. Сума сторін трикутника МKР дорівнює 105 см. Чому дорівнює периметр трикутника М1K1Р1?
а) 52,5 см; б) 210 см; в) 60 см; г) 105 см.
9. Трикутник ACD рівнобедрений з основою AD. CK — висота, проведена до основи. ÐАСK = 36°. Чому дорівнює ÐACD?
а) 36°; б) 18°; в) 72°; г) 90°.
10. Знайти довжину гіпотенузи АВ трикутника АВС (див. рис.).
а) 12 см; б) 6 см;
в)  см; г) 24 см.
| 
|
Середній рівень
1. За рисунком знайти градусну міру кута С та довжину відрізка ВО. 
2. У трикутнику АВС: АС = 6 см, АВ = 14 см. Знайти довжину сторони ВС, якщо периметр трикутника дорівнює 30 см.
3. Точка О — середина відрізка РD. За рисунком довести, що трикутник РОМ дорівнює трикутнику ОDС. 
4. Чи буде трикутник MKN рівнобедреним (див. рис.)? Пояснити. 
Достатній рівень
1. На сторонах ОХ і ОY кута ХОY відкладені рівні відрізки ОМ і ОN відповідно. Довести, що відстані від будь-якої точки А бісектриси цього кута до точок М і N рівні. 
2. Дано: DMNK = DРСD, MN = 13 см, МK = 8 см. Сторона СD на 6 см менша від сторони РС. Знайти периметр трикутника РСD.
3. У трикутнику MNK проведено медіану NA. Сторона NK дорівнює 9 см, а NM на 3 см менша від неї. Знайти довжину відрізка МА, якщо периметр трикутника дорівнює 25 см. 
4. Довести рівність прямокутних трикутників за гіпотенузою і гострим кутом.
5. Знайти кути рівнобедреного трикутника, якщо один з них на 30° менший від іншого (розглянути два випадки).
Високий рівень
1. Промінь СА — бісектриса кута ВСВ1, ÐВАМ = ÐВ1АМ. Довести, що ВС = В1С.
2. Трикутники АВС і А1В1С1 рівні. Сторона АВ більша від сторони В1С1 на 5 см, а сторона А1С1 удвічі менша від сторони ВС. Знайти сторони трикутника А1В1С1, якщо периметр трикутника АВС дорівнює 40 см.
3. Дано: Ð1 = Ð2, Ð3 = Ð4 (див. рис.). 
Довести: DАМС — рівнобедрений.
4. У рівнобедреному трикутнику АВС з основою АВ проведена бісектриса СK. Периметр трикутника АСK дорівнює 21 см, а периметр трикутника АВС дорівнює 36 см. Знайти довжину бісектриси.
5. Довести рівність прямокутних трикутників за катетом і медіаною, проведеною до іншого катета.
ІІІ Варіант
Початковий рівень
1. Два трикутники АВС і MNK будуть рівними, якщо в них...
а) ÐА = ÐМ, ÐВ = ÐN, ÐC = ÐK;
б) АВ = МN, ВС = NK, АС = МK, ÐА ¹ ÐМ, ÐВ ¹ ÐN, ÐС ¹ ÐK;
в) АВ = MN, ВС = NK, АС = МK;
г)АВ = MN, ÐA = ÐM.
2. Дано: DМKР = DМ1K1Р1. Вказати правильну рівність.
а) ÐМ = ÐР1; б) ÐK = ÐK1; в) KР = K1Р1; г) МK = М1Р1.
3. Ознака рівності трикутників (за двома сторонами і кутом між ними).
Два трикутники будуть рівними, якщо..
а) дві сторони одного трикутника дорівнюють відповідно двом сторонам іншого трикутника,
б) дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника,
в) сторона і кут одного трикутника відповідно дорівнюють стороні та куту іншого трикутника;
г)два кути одного трикутника дорівнюють двом кутам іншого трикутника.
4. Трикутники MNK і АВС рівні. Відповідними до сторони NK і кута А є...
а) BC; ÐM; б) AC; ÐN; в) AB; ÐK; г) CA; ÐK.
5. Дано: DАВС і DА1В1С1, АВ = 7 см, А1В1 = 7 см, ВС = 13 см, ÐВ = 64°, ÐВ1 = 64°. Щоб трикутник АВС дорівнював трикутнику А1В1С1, потрібно, щоб сторона B1C1 дорівнювала...
а) 7 см; б) 20 см; в) 13 см; г) 5 см.
6. Трикутник АВС — рівнобедрений з основою AC. ÐА = 75°, АВ = 13 см. Знайти кут С і сторону ВС. 
а) 13°; 75 см; б) 75°; 13 см;
в) 75°; 26 см; г) 26°; 6,5 см.
7. У трикутнику АВС: АВ = 6 см, ÐA = 75°, ÐB = 40°, у трикутнику KРD: KD = 6 см, ÐK = 75°, ÐD = 40°. Вказати правильне твердження.
а) DАВС = DDРK; б) DАВС = DKРD;
в) DАВС = DKDР; г) DАВС = DРKD.
8. Трикутники АВС і МKD рівні. Сторони трикутника МKD дорівнюють: МK = 16 см, KD = 9 см, DМ = 20 см. Знайти сторони АВ, ВС, АС трикутника АВС.
а) 9 см, 16 см, 20 см; б) 16 см, 9 см, 20 см;
в) 16 см, 20 см, 20 см; г) 9 см, 18 см, 16 см.
9. Трикутник XYZ — рівнобедрений з основою XZ, YM — медіана, проведена до основи. Тоді кут YMZ дорівнює...
а) 30°; б) 60°; в) 90°; г) 45°.
| 10. Знайти довжину гіпотенузи РK трикутника PNK (див. рис.). а) 12 см; б) 24 см; в) 6 см; г) 36 см. | 
|
Середній рівень
1. За рисунком вказати кут, градусна міра якого дорівнює 64°, та відрізок, довжина якого дорівнює 17 см. 
2. У трикутнику АВС АВ = 7 см, АС = 18 см, а його периметр — 37 см. Знайти довжину сторони ВС.
| 3. Трикутник ВОD рівнобедрений з основою ВD. Користуючись рисунком, довести, що трикутник АВО дорівнює трикутнику СDО. | 
|
| 4. Чи буде трикутник АВС рівнобедреним (див. рис.)? Пояснити. | 
|
Достатній рівень
1. Відрізки АВ і MN перетинаються в точці О, МО = ОВ, ÐАМС = ÐNВD. Довести, що відрізок АО дорівнює відрізку NО.
2. Дано: DАВС = DMNP, АВ = 6 см, ВС = 8 см. Сторона АС на 3 см більша від сторони MN. Знайти периметр трикутника MNP.
3. У трикутнику MNP проведена медіана МА. Сторона MN дорівнює 6 см, а МР удвічі більша від неї. Знайти довжину відрізка NА, якщо периметр трикутника дорівнює 32 см. 
4. Довести рівність прямокутних трикутників за катетом і гострим кутом.
5. Знайти кути рівнобедреного трикутника, якщо один з них на 50° більший від іншого (розглянути два випадки).
Високий рівень
1. Дано: Ð1 = Ð2, Ð3 = Ð4. Довести: СО = ОD.
2. Трикутник MNK дорівнює трикутнику М1N1K1. Сторона МK менша від сторони N1K1 на 5 см, а сторона М1N1 удвічі більша від сторони MK. Знайти сторони трикутника MNK, якщо периметр трикутника M1N1K1 дорівнює 65 см.
3. Дано: Ð1 = Ð2, Ð3 = Ð4 (див. рис.). 
Довести: DАВС — рівнобедрений.
4. У рівнобедреному трикутнику KMN з основою KN проведена висота МА. Периметр трикутника KМА дорівнює 16 см, а периметр трикутника KMN дорівнює 42 см. Знайти довжину висоти.
5. Довести рівність прямокутних трикутників за катетом і бісектрисою, проведеною до цього катета.
ІV Варіант
Початковий рівень
1. Два трикутники будуть рівними, якщо...
а) три кути одного трикутника дорівнюють трьом кутам іншого трикутника;
б) дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними іншого трикутника;
в) сторона і кут одного трикутника відповідно дорівнюють стороні та куту іншого трикутника;
г)дві сторони одного трикутника дорівнюють двом сторонам іншого трикутника.
2. Дано: DАВС = DА1В1С1. Вказати правильну рівність.
а) АС = В1С1; б) АВ = А1В1;
в) ÐВ = ÐА1; г) ÐАСВ = ÐАВ1С1.
3. Ознака рівності трикутників (за стороною і двома прилеглими до неї кутами). Два трикутники MNK і АВС будуть рівними, якщо...
а) ÐМ = ÐА; ÐK = ÐС; б) MN = АВ; NK = ВС;
в) MN = АВ; ÐМ = ÐА; ÐN = ÐВ; г) MN = АВ, ÐM = ÐC, ÐN = ÐA.
4. Трикутники ABC і DKP рівні. Відповідними до сторони AB і кута P є...
а) DP; ÐA; б) DK; ÐC; в) KP; ÐA; г) PD; ÐB.
5. Дано: DАВС і DKMN, ВС = 7 см, NK = 7 см. ÐN = 70°, ÐK = 30°. Щоб трикутники АВС і МNK були рівними, потрібно, щоб...
а) ÐB = 30°, ÐC = 70°; б) ÐB = 30°, ÐC = 100°;
в) ÐB = 70°, ÐC = 30°; г) ÐB = 100°, ÐC = 70°.
6. Трикутник MNK рівнобедрений з основою MK. Вказати правильну рівність. 
а) MN = NK; б) MN = MK;
в) ÐN = ÐM; г) ÐN = ÐK.
7. У рівнобедреному трикутнику АВС з основою АВ сторона АС = 17 см, ÐВ = 53°. Знайти довжину сторони ВС та кут А.
а) 53 см, 17°; б) 17 см, 53°; в) 53 см, 60°; г) 20 см, 17°.
8. Трикутник МKР дорівнює трикутнику СDN, МK = 8 см, KР = 11 см, МР = 17 см. Яка сторона трикутника СDN дорівнює 11 см?
а) CD; б) DN; в) CN; г) MP.
9. Трикутник МKN — рівнобедрений з основою MN. KD — висота, проведена до основи. Чому дорівнює MN, якщо MD = 8 см?
а) 8 см; б) 16 см; в) 4 см; г) 2 см.
| 10. Знайти довжину гіпотенузи МK трикутника MNK (див. рис.). а) 8 см; б) 16 см; в) 4 см; г) 30 см. | 
|
Середній рівень
1. За рисунком вказати кут, градусна міра якого дорівнює 118°, та сторону завдовжки 13 см. 
2. У трикутнику MNK: MN = 18 см, NK = 8 см. Знайти довжину сторони МK, якщо периметр трикутника дорівнює 45 см.
3. Трикутник ВМС рівнобедрений з основою ВС. Користуючись рисунком, довести, що трикутник АВМ дорівнює трикутнику DСМ.
4. Чи буде трикутник MNK рівнобедреним (див. рис.)? Пояснити.
Достатній рівень
1. Промінь АС — бісектриса кута ВАD, а промінь СА — бісектриса кута ВСD. Довести, що АВ = АD.
2. Дано: DАВС = DDМN, ВС = 11 см, DМ = 14 см, а сторона DN удвічі довша від сторони MN. Знайти периметр трикутника АВС.
3. У трикутнику KРD проведено медіану KM. Сторона DK дорівнює 18 см, а сторона KР менша від неї утричі. Знайти довжину відрізка МР, якщо периметр трикутника дорівнює 44 см.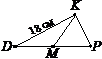 
4. Довести, що катет прямокутного трикутника, який лежить проти кута 30°, дорівнює половині гіпотенузи.
5. Знайти кути рівнобедреного трикутника, якщо один з них менший від іншого на 50° (розглянути два випадки).
Високий рівень
1. Дано: Ð1 = Ð2, NO = OK. 
Довести: MN = KР.
2. Трикутник MNK дорівнює трикутнику M1N1K1. Сторона М1K1 утричі менша від сторони NK, а сторона MN на 6 см більша від N1K1. Знайти сторони трикутника MNK, якщо периметр трикутника М1N1K1 дорівнює 55 см.
3. Дано: АD = KС, Ð1 = Ð2 (див. рис.). Довести: DАВС — рівнобедрений.
4. У рівнобедреному трикутнику АВС з основою BС проведена медіана АМ. Периметр трикутника АВМ дорівнює 25 см, а периметр трикутника АВС дорівнює 38 см. Знайти довжину медіани.
5. Довести рівність прямокутних трикутників за катетом і бісектрисою, проведеною до гіпотенузи.
Тематична атестація №5.
Коло. Геометричні побудови
І Варіант
Початковий рівень
1. Фігуру, що складається з усіх точок площини, які рівновіддалені від даної точки, називають...
а) відрізком; б) кутом; в) колом; г) бісектрисою.
2. Вказати правильне твердження. 
а) KВ — діаметр кола;
б) АМ — дотична до кола;
в) АВ — радіус кола;
г) СD — діаметр кола.
| 3. BK —дотична до кола. Тоді кут OBK дорівнює... а) 0°; б) 60°; в) 90°; г) 180°. | 
|
| 4. Пряма МО — серединний перпендикуляр до відрізка АВ. АМ = 7 см. Чому дорівнює довжина відрізка МВ? |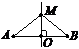 
|
а) 14 см; б) 3,5 см; в) 7 см; г) 17 см.
5. Вказати рисунок, на якому зображено трикутник, вписаний у коло.
| 
| 
| 
|
| а) | б) | в) | г) |
6. Задана точка А, коло з центром О і радіусом 5 см. Де розміщена точка А відносно кола, якщо ОА = 3 см?
а) Зовні кола; б) усередині кола;
в) на колі; г) не можна визначити.
7. Два кола з центрами в точках О1 і О2 та радіусами 23 см і 11 см мають зовнішній дотик. Як знайти відстань О1О2 між центрами кіл?
а) 23 см + 11 см;
б) 23 см – 11 см;
в) 23 см × 2;
г) 11 см × 2.
8. Точка О — центр кола, описаного навколо трикутника АВС. Вказати правильне твердження.
а) OМ — радіус кола;
б) ÐОМС = 60°;
в) ÐONB = 100°;
г) ОN — проходить через середину сторони BC.
9. Центр кола, вписаного у трикутник, є точкою перетину...
а) висот трикутника;
б) серединних перпендикулярів до сторін трикутника;
в) бісектрис трикутника;
г) медіан трикутника.
10. Точка О — центр кола, вписаного у трикутник АВС, у якого ÐА = 62°. Чому дорівнює ÐВАО?
а) 62°; б) 124°; в) 31°; г) 28°.
Середній рівень
1. Дано: СD^MN, MN = 18 см (див. рис.). Знайти МK.
2. Кола, діаметри яких дорівнюють 8 см і 12 см, мають зовнішній дотик. Знайти відстань між центрами цих кіл.
3. Радіус кола, описаного навколо прямокутного трикутника, дорівнює 6 см. Чому дорівнює гіпотенуза трикутника?
4. Побудувати трикутник за двома сторонами MN = 2 см, МK = 5 см і кутом між ними, який дорівнює 50°.
Достатній рівень
1. Побудувати рівнобедрений трикутник за основою і бісектрисою, проведеною до основи.
2. Два кола мають внутрішній дотик. Знайти радіуси цих кіл, якщо один з них у 5 разів більший від іншого, а відстань між центрами кіл дорівнює 36 см.
3. Радіуси вписаного й описаного навколо рівностороннього трикутника кіл відповідно дорівнюють 3 см і 6 см. Знайти висоту трикутника.
4. X, Y, Z — точки дотику вписаного кола до сторін АВ, ВС, АС трикутника АВС. Знайти сторони і периметр трикутника, якщо AX = 3 см, BY = 6 см, CZ = 5 см.
5. На даній прямій а знайти точку, рівновіддалену від заданих точок М і N.
Високий рівень
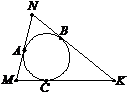1. У трикутник MNK вписано коло, А, В, С — точки дотику кола до його сторін MN, NK, МK. Знайти довжину відрізка NВ, якщо АМ = 4 см, ВK = 9 см, а периметр трикутника дорівнює 36 см.
2. Дано три точки М, N, K, які не лежать на одній прямій. Побудувати точку, яка розміщена на відстані h від точки K, рівновіддалену від точок М і N.
3. У колі з центром О проведена хорда MN. Через точку М проведена дотична АВ до кола. Знайти менший з кутів між дотичною і хордою, якщо ÐMON = 40°.
4. Побудувати трикутник за двома сторонами та медіаною, проведеною до однієї з них.
5. Побудувати трикутник за стороною, висотою, проведеною до цієї сторони, та радіусом описаного кола.
ІІ Варіант
Початковий рівень
1. Яка фігура складається з усіх точок площини, рівновіддалених від даної точки?
а) Пряма; б) відрізок; в) промінь; г) коло.
| 2. АМ — дотична до кола. Тоді кут DAM дорівнює... а) 180°; б) 0°; в) 90°; г) 60°. |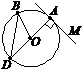 
|
3. Вказати правильне твердження. 
а) MN — діаметр кола;
б) FP — дотична до кола;
в) MM — радіус кола;
г) FK — хорда.
| 4. Пряма CD — серединний перпендикуляр до відрізка АВ. Чому дорівнює довжина відрізка AC, якщо СВ = 12 см? | 
|
а) 10 см; б) 6 см; в) 24 см; г) 12 см.
5. Коло називають описаним навколо трикутника, якщо воно...
а) проходить через дві вершини трикутника;
б) проходить через три вершини трикутника;
в) дотикається до всіх сторін трикутника;
г) дотикається до однієї сторони трикутника.
6. Задана точка М і коло з центром О, радіус якого дорівнює 15 см. Де розміщені відносно кола точка М, якщо ОМ = 15 см?
а) На колі; б) поза колом;
в) всередині кола; г) не можна визначити.
7. Два кола, радіуси яких відповідно дорівнюють R1 і R2, з центрами в точках О1 і О2, мають зовнішній дотик. Як знайти відстань між центрами кіл?
а) R2 – R1, б) 2R1;
в) R1 + R2; г) 2R2.
8. Точка О — центр кола, описаного навколо трикутника MNK. Вказати правильне твердження. 
а) МD = DN;
б) ОD||MN;
в) ÐОРK = 60°;
г) ОР — радіус описаного кола.
9. Точка перетину бісектрис трикутника є...
а) центром кола, описаного навколо трикутника;
б) центром кола, вписаного у трикутник;
в) точкою перетину медіан трикутника;
г)вершиною трикутника.
10. Точка О — центр кола, вписаного у трикутник CBD, у якого ÐВ = 58°. Чому дорівнює ÐСВО?
а) 32°; б) 58°; в) 116°; г) 29°.
Середній рівень
| 1. Дано: СD^MN, MK = 9 см. Знайти: МN. | 
|
| 2. Кола з діаметрами 22 см і 14 см мають внутрішній дотик. Знайти відстань між центрами цих кіл. | 
|
3. Гіпотенуза прямокутного трикутника дорівнює 16 см. Чому дорівнює радіус кола, описаного навколо цього трикутника?
4. Побудувати трикутник АВС, у якого АВ = 3 см, ÐА = 60° і ÐВ = 70°.
Достатній рівень
1. Побудувати рівнобедрений трикутник за бічною стороною і бісектрисою, проведеною до основи.
2. Два кола мають зовнішній дотик. Знайти радіуси цих кіл, якщо один з них утричі менший від іншого, а відстань між центрами кіл дорівнює 72 см.
3. Висота рівностороннього трикутника дорівнює 18 см. Чому дорівнює радіус описаного кола, якщо радіус вписаного кола дорівнює 6 см?
4. А, В, С — точки дотику вписаного кола до сторін MN, NK, MK трикутника MNK. Знайти сторони і периметр трикутника MNK, якщо MA = 13 см, NB = 11 см, KC = 6 см.
5. На сторонах кута АОВ знайти точки, рівновіддалені від точок М і N (див. рис.).
Високий рівень
1. У трикутник АВС вписано коло. X, Y, Z — точки дотику кола до його сторін АВ, ВС, АС. Знайти довжину відрізка ВХ, якщо АZ = 7 см, ZС = 11 см, а периметр трикутника дорівнює 44 см.
2. Дано пряму d і точку М. Знайти точку, яка віддалена від прямої d на відстань h, а від точки М — на відстань b.
3. Через точку Р кола з центром у точці О проведена хорда PD і дотична АВ. Менший кут між дотичною і хордою дорівнює 50°. Знайти кут POD.
4. Побудувати трикутник за стороною, прилеглим до неї кутом і медіаною, проведеною до цієї сторони.
5. Побудувати рівнобедрений трикутник за кутом при вершині та радіусом описаного кола.
ІІІ Варіант
Початковий рівень
1. Як називають фігуру, яка складається з усіх точок площини, віддалених від даної точки А на 3 см?
а) Відрізок; б) коло; в) бісектриса; г) промінь.
| 2. АМ — дотична до кола в точці А. Тоді кут ОАМ дорівнює.... а) 90°; б) 180°; в) 0°; г) 60°. | 
|
3. Вказати правильне твердження. 
а) ОС — радіус кола;
б) MN — діаметр кола;
в) DB — хорда;
г) DO — дотична до кола.
4. Діаметр кола дорівнює 25 см. Знайти радіус цього кола.
а) 25 см; б) 50 см; в) 12,5 см; г) 5 см.
5. Вказати рисунок, на якому зображено трикутник, описаний навколо кола.
| 
| 
| 
|
| а) | б) | в) | г) |
6. Задано коло з центром О і пряма CD. Як розміщена пряма відносно кола, якщо радіус кола дорівнює 7 см, а відстань від точки О до прямої дорівнює 6 см?
а) Перетинає коло; б) дотикається до кола;
в) не перетинає кола; г) не можна визначити.
7. Два кола, радіуси яких дорівнюють 15 см і 7 см, а центри містяться у точках О1 і О2, мають внутрішній дотик. Як знайти відстань О1О2 між центрами кіл?
а) 15 см + 7 см; б) 15 см – 7 см;
в) 2 × 15 см; г) 2 × 7 см.
8. Центр кола, описаного навколо трикутника, є точкою перетину його...
а) висот; б) медіан; в) бісектрис;
г) перпендикулярів, проведених до сторін трикутника через їх середини.
9. Точка О — центр кола, вписаного у трикутник ABC. Вказати правильне твердження:
а) ÐСВО = ÐАВО;
б) О — точка перетину медіан трикутника;
в) ÐСАО > ÐВАО;
г)AO^CB.
10. Дотик двох кіл буде зовнішнім, якщо центри кіл лежать...
а) по один бік від їх спільної дотичної;
б) по різні боки від їх спільної дотичної;
в) на прямій, яка не проходить через точку дотику кіл;
г)на дотичній.
Середній рівень
1. Діаметр СD кола проходить через середину K хорди MN. Яка градусна міра кута ОKN?
2. Чи будуть дотикатися два кола і мати зовнішній дотик, якщо їх радіуси дорівнюють 15 см і 22 см, а відстань між центрами кіл — 37 см?
3. Гіпотенуза прямокутного трикутника дорівнює 18 см. Чому дорівнює радіус кола, описаного навколо цього трикутника?
4. Поділити даний кут на дві рівні частини.
Достатній рівень
1. Побудувати рівнобедрений трикутник за бічною стороною і висотою, проведеною до основи.
2. Два кола мають внутрішній дотик. Знайти радіуси кіл, якщо вони відносяться як 2 : 3, а відстань між центрами кіл дорівнює 17 см.
3. Радіуси вписаного й описаного кіл навколо рівностороннього трикутника відповідно дорівнюють 5 і 10 см. Чому дорівнює бісектриса трикутника?
4. Точки А1, В1, С1 — точки дотику вписаного кола до сторін MN, NP, PM трикутника MNP. Знайти сторони та периметр трикутника, якщо MA1 = 14 см, NB1 = 3 см, PC1 = 12 см.
5. На даному колі знайти точки, рівновіддалені від двох заданих точок А і В.
Високий рівень
1. У трикутник АВС вписано коло, X, Y, Z — точки дотику кола до його сторін АВ, ВС, АС. Знайти периметр трикутника АВС, якщо АZ = 8 см, ZС = 9 см, ВY = 7 см.
2. Дано чотири точки А, В, С, D, будь-які три з яких не лежать на одній прямій. Знайти точку, рівновіддалену від точок А та В і від точок С та D.
3. У колі з центром О проведена хорда CD. Через точку С проведена дотична XY. Знайти менший з кутів між дотичною і хордою, якщо ÐСOD = 80°.
4. Побудувати трикутник за двома сторонами та висотою, проведеною до однієї з них.
5. Побудувати трикутник за стороною, прилеглим кутом і радіусом описаного кола.
ІV Варіант
Початковий рівень
1. Яку фігуру утворюють усі точки площини, віддалені від даної прямої а на 2 см?
а) Пряму; б) коло;
в) дві прямі, що перетинаються;
г) дві прямі, паралельні даній, що розміщені по різні боки від неї.
2. За рисунком вказати правильне твердження 
.
а) MN — діаметр кола;
б) ОР — хорда;
в) ОМ ¹ ОР;
г) NK — хорда.
3. Коло називають вписаним у трикутник, якщо воно...
а) проходить через вершини трикутника;
б) дотикається до всіх сторін трикутника;
в) дотикається до двох сторін трикутника;
г) не дотикається до сторін трикутника.
4. Діаметр кола дорівнює 7 см. Знайти його радіус.
а) 7 см; б) 3,5 см; в) 14 см; г) 21 см.
5. Вказати рисунок, на якому зображено трикутник, навколо якого описано коло.
| 
| 
| 
|
| а) | б) | в) | г) |
6. Задано коло з центром А і пряма KD. Як розміщена пряма відносно кола, якщо радіус кола дорівнює 3 см, а відстань від точки А до заданої прямої дорівнює 5 см.
а) Перетинає коло; б) не перетинає кола;
в) дотикається до кола; г) не можна визначити.
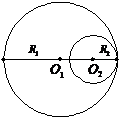7. Два кола з центрами в точках О1 і О2, радіуси яких дорівнюють відповідно R1 і R2, мають внутрішній дотик. Як знайти відстань між центрами кіл?
а) R1 + R2;
б) R1 – R2;
в) R1 – 2R2;
г) 2R2.
8. Центр кола, вписаного у трикутник, є точкою перетину...
а) висот трикутника;
б) медіан трикутника;
в) бісектрис трикутника;
г) перпендикулярів, проведених до сторін трикутника через їх середини.
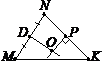9. Точка О — центр кола, описаного навколо трикутника MNK. Вказати правильне твердження.
а) ON — діаметр описаного кола;
б) ОD — радіус описаного кола;
в) NP = РK;
г) ÐОDN = 60°.
10. Точка О — центр кола, вписаного у трикутник MKD, у якого ÐOKD = 26°. Чому дорівнює кут MKD трикутника?
а) 26°; б) 13°; в) 52°; г) 64°.
Середній рівень
1. За рисунком знайти довжину діаметра та довжину хорди АВ.
2. Чи будуть дотикатися два кола й мати зовнішній дотик, якщо їх радіуси дорівнюють 11 см і 4 см, а відстань між їх центрами — 14 см?
3. Гіпотенуза прямокутного трикутника дорівнює 12 см. Чому дорівнює радіус кола, описаного навколо цього трикутника?
4. Побудувати рівнобедрений трикутник за основою та кутом при основі.
Достатній рівень
1. Побудувати рівнобедрений трикутник за бічною стороною і медіаною, проведеною до основи.
2. Два кола мають внутрішній дотик. Знайти радіуси кіл, якщо один з них менший від іншого у 3 рази, а відстань між центрами дорівнює 24 см.
3. Радіуси вписаного й описаного кіл навколо рівностороннього трикутника дорівнюють 9 см і 18 см. Знайти медіану трикутника.
4. M, N, K — точки дотику вписаного кола до сторін AC, CD і AD трикутника ACD. Знайти сторони і периметр трикутника, якщо AM = 7 см, CN = 8 см, DK = 10 см.
5. На прямих а і b знайти точки, віддалені від заданої точки М на відстань h.
Високий рівень
1. У трикутник MNK вписано коло. А, В, С — точки дотику кола до сторін MN, NK, MK. Знайти довжину відрізка NB, якщо МС = 10 см, ВK = 13 см, а периметр трикутника дорівнює 52 см.
2. Дано дві точки А і В та пряму d, що не проходить через задані точки. Знайти точки, рівновіддалені від двох заданих точок А і В, і віддалені від даної прямої на відстань h.
3. У колі з центром О проведена хорда PK. Через точку K проведена до кола дотична АВ. Кут AKР = 60°. Знайти кут POK.
4. Побудувати трикутник за стороною, прилеглим до неї кутом і висотою, проведеною до заданої сторони.
5. Побудувати трикутник за стороною, бісектрисою, проведеною до цієї сторони через задану на ній точку (основу бісектриси), та радіусом описаного кола.
Підсумкова Тематична атестація №6
Варіант 1
Початковий рівень
1. На відрізку МN завдовжки 23 см позначена точка K. Знайти довжину відрізка МK, якщо довжина відрізка KN дорівнює 14 см.
а)37 см; б)9 см; в) 14 см; г)23 см.
2. Які кути можуть бути суміжними?
а)20°, 170°; б)65°, 125°; в)140°, 40°; г)100°, 70°.
3. DАВС = DMNK. Вказати правильні рівності.
а) AB = NK; б)ÐВ = ÐN; в)ÐС = ÐМ; г)АС = МK.
4. Якою має бути градусна міра кута x, щоб прямі а і b були паралельними?
а)105°; б)175°;
в)25°; г)75°.
5. Діаметр кола дорівнює 28 см. Його радіус дорівнює:
а)28 см; б)14 см; в)56 см; г)8 см.
6. У трикутнику СDМ: СD = 18 см, DМ = 11 см, СМ = 13 см. Знайти його периметр.
а)42 см; б)24 см; в)29 см; г)31 см.
7. Два кути трикутника дорівнюють 30° і 45°. Знайти третій кут.
а)75°; б)105°; в)150°; г)135°.
8. Якщо точка M належить серединному перпендикуляру MO до відрізка AB, то 
...
а)AМ = МО; б)AМ = AO;
в)MB = AO; г)AМ = MB.
9. Відстань від точки О до прямої b дорівнює 
...
а)8 см; б)5 см;
в)3 см; г)не можна визначити.
10. Вказати правильне твердження.
а)Центром кола, описаного навколо трикутника, є точка перетину серединних перпендикулярів до його сторін;
б)бісектриса трикутника ділить протилежну сторону навпіл;
в)якщо дві сторони одного трикутника дорівнюють відповідно двом сторонам другого трикутника, то такі трикутники рівні;
г)у рівнобедреному трикутнику кути при основі не рівні.
Середній рівень
1. У трикутнику АВС сторони АВ і ВС відповідно дорівнюють 13 см і 8 см, а сторона АС менша від сторони АВ на 6 см. Знайти периметр трикутника.
2. Один з гострих кутів прямокутного трикутника дорівнює 17°. Знайти інший гострий кут трикутника.
| 3. За рисунком вказати, який кут трикутника АСD дорівнює 82°. | 
|
| 4. Чи є прямі a і b паралельними? |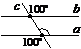 
|
Достатній рівень
1. У трикутнику АВС сторона ВС дорівнює 11 см, а сторона АС більша від сторони АВ на 3 см. Знайти невідомі сторони трикутника, якщо його периметр дорівнює 34 см.
2. У рівнобедреному трикутнику кут при основі у 7 разів більший від кута між бічними сторонами. Знайти кути трикутника.
3. У рівнобедреному трикутнику АВС з основою АС проведена медіана ВK. Знайти периметр трикутника, якщо АВ = 6 см, АK = 4 см. 
| 4. Довести рівність трикутників АВС і NMK. | 
|
5. Через точку B кола проведено діаметр, хорду та дотичну. За рисунком знайти менший з кутів між хордою і дотичною.
Високий рівень
1. Точки М і N розміщені по різні боки від прямої АВ так, що МА = NА, МВ = NB. Х — довільна точка відрізка АВ. Довести, що кут АХМ дорівнює куту АXN.
2. Одна сторона трикутника дорівнює 27 см. Дві інші сторони відносяться як 5 : 3, а їх різниця дорівнює 20 см. Знайти периметр трикутника.
3. АВ і MN — діаметри кола з центром у точці О. Довести, що прямі АМ і ВN — паралельні.
4. У трикутнику АВС кут А дорівнює 56°, кут С дорівнює 48°. Визначити градусну міру тупого кута між бісектрисами трикутника, проведеними з цих вершин.
5. Побудувати трикутник за стороною, медіаною, проведеною до цієї сторони, якщо відомо, що вершина, протилежна заданій стороні, розміщена на відстані b від деякої заданої точки М.
Варіант 2
Початковий рівень
1. На відрізку AX позначена точка В. Відомо, що АВ = 7 см. Знайти довжину відрізка ВХ, якщо відрізок АХ дорівнює 11 см.
а) 18 см; б)11 см; в) 4 см; г)77 см.
2. Один із двох суміжних кутів дорівнює 70°. Знайти інший кут.
а)100°; б)110°; в)130°; г)140°.
3. Трикутник MNK дорівнює трикутнику CDP. Вказати правильні рівності.
а)NK = DP; б)ÐN = ÐP; в)ÐС = ÐМ; г)CD = МK.
4. Якою має бути градусна міра кута х, щоб прямі а і b були паралельними?
а)54°; б)108°;
в)126°; г)36°.
5. Якщо радіус кола дорівнює 12 см, то його діаметр дорівнює...
а)12 см; б)6 см; в) 24 см; г)36 см.
6. У рівнобедреному трикутнику бічна сторона дорівнює 7 см, а основа — 11 см. Знайти його периметр.
а)14 см; б)18 см; в)25 см; г)22 см.
7. Два кути трикутника дорівнюють 50° і 60°. Знайти третій кут.
а)110°; б)120°; в)130°; г)70°.
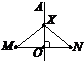8. Якщо точка Х належить серединному перпендикуляру AO до відрізка MN і ХM = 15 см, то...
а)ON = 15 см; б)MO = 15 см;
в)XN = 15 см; г)OX = 15 см.
9. Катет АС прямокутного трикутника АВС (ÐС = 90°) дорівнює 7 см. Чому дорівнює відстань від точки А до прямої СВ?
а)14 см; б) 7 см;
в)3,5 см; г)не можна визначити.
10. Вказати правильне твердження.
а)У рівнобедреному трикутнику медіана, проведена до основи, є і висотою;
б)бісектриса ділить трикутник на два рівні трикутники;
в)центром кола, вписаного у трикутник, є точка перетину бісектрис;
г)якщо три кути одного трикутника відповідно дорівнюють трьом кутам другого трикутника, то такі трикутники рівні.
Середній рівень
1. У трикутнику MNK сторони MN і NK відповідно дорівнюють 17 см і 5 см, а сторона MK більша від сторони NK на 10 см. Знайти периметр трикутника.
2. Два кути трикутника дорівнюють 50° і 70°. Знайти зовнішній кут трикутника при вершині третього кута.
| 3. За рисунком вказати, який кут трикутника OKP дорівнює 40°. | 
|
4. Чи будуть прямі m і n паралельні?
Достатній рівень
1. У трикутнику MNC сторона MN більша від сторони NC на 5 см, а сторона МC дорівнює 20 см. Знайти невідомі сторони трикутника, якщо його периметр дорівнює 45 см.
2. У рівнобедреному трикутнику кут між бічними сторонами утричі більший від кута при основі. Знайти кути трикутника.
3. У рівнобедреному трикутнику АВС з основою АС проведена медіана АМ. Знайти периметр трикутника, якщо АС = 8 см, МС = 6 см. 
| 4. Довести рівність трикутників АВС і MNK. | 
|
| 5. Через точку В кола проведено діаметр, хорду та дотичну. За рисунком знайти кут між хордою та діаметром. | 
|
Високий рівень
1. Точки Р і K розміщені по різні боки від прямої АВ так, що АР = АK, РВ = KВ. Довести, що бісектриси ВС і ВD трикутників АВР і АВK рівні.
2. Одна сторона трикутника дорівнює 8 см. Дві інші відносяться як 3 : 5, а їх різниця дорівнює 6 см. Знайти периметр трикутника.
3. АВ — діаметр кола, АМ і ВN — рівні хорди (див. рис.). Довести, що прямі АМ і ВN паралельні.
4. У трикутнику АСD кут А дорівнює 70°, кут D дорівнює 60°. Знайти градусну міру тупого кута між бісектрисами трикутника, проведеними з цих вершин.
5. Побудувати трикутник за стороною, прилеглим кутом, якщо відомо, що вершина, протилежна заданій стороні, розміщена на відстані b від деякої заданої точки М.
Варіант 3
Початковий рівень
1. На промені ОA позначена точка В. Відомо, що ОВ = 7 см, ОА = 32 см. Знайти довжину відрізка АВ.
а)32 см; б)39 см; в ) 25 см; г)14 см.
2. Один із двох суміжних кутів дорівнює 35°. Інший кут дорівнює...
а)45°; б)145°; в)65°; г)165°.
3. Трикутник XYZ дорівнює трикутнику ABC. Вказати правильні рівності.
а)ÐX = ÐC; б)ÐY = ÐB; в)XZ = AB; г)YZ = BC.
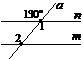4. Дано: m||n, а — січна. Знайти: Ð1 і Ð2.
а)50° і 50°; б)130° і 130°;
в)50° і 130°; г)40° і 65°.
5. У рівнобедреному трикутнику бічна сторона дорівнює 7 см, а основа — 13 см. Знайти його периметр.
а)20 см; б)26 см; в)14 см; г)27 см.
6. Якщо два кути трикутника дорівнюють 20° і 85°, то третій кут трикутника дорівнює...
а)105°; б)95°; в)160°; г)75°.
7. Два кола з радіусами 8 см і 5 см мають зовнішній дотик. Знайти відстань між центрами кіл.
а)10 см; б)13 см; в)3 см; г)16 см.
8. Пряма CD — серединний перпендикуляр до відрізка AB. Відомо, що CB = 11 см. Тоді AC дорівнює...
а)5,5 см; б)22 см;
в)11 см; г)не можна знайти.
9. MD — висота трикутника АВM. Відомо, що MA = 7 см, MD = 3 см, MB = 4 см. Чому дорівнює відстань від точки M до прямої AВ?
а)7 см; б)3 см;
в)4 см; г)14 см.
10. Вказати правильне твердження.
а)Точка перетину висот трикутника є центром вписаного в нього кола;
б)дотична до кола перпендикулярна до радіуса, проведеного в точку дотику;
в)у рівнобедреному трикутнику бісектриса, проведена до основи, є і медіаною;
г)якщо кут і сторона одного трикутника відповідно дорівнюють куту і стороні другого трикутника, то такі трикутники рівні.
Середній рівень
1. У трикутнику АСD сторони АС і СD відповідно дорівнюють 6 см і 9 см, а сторона АD удвічі більша від сторони АС. Знайти периметр трикутника.
2. Зовнішній кут трикутника дорівнює 125°. Чому дорівнює сума двох внутрішніх кутів трикутника, не суміжних з ним?
| 3. За рисунком вказати, який кут трикутника АВМ дорівнює 65°. | 
|
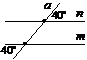4. Чи будуть прямі m і n паралельні?
Достатній рівень
1. У трикутнику MNK сторона МK дорівнює 18 см, а сторона MN менша від сторони NK на 3 см. Знайти невідому сторону трикутника, якщо його периметр дорівнює 51 см.
2. У рівнобедреному трикутнику кут при основі у 2 рази менший від кута між бічними сторонами. Знайти кути трикутника.
3. У трикутнику АВС проведені медіани ВК і СМ. Знайти периметр трикутника, якщо ВС = 13 см, СК = 5 см, ВМ = 3 см.
4. Довести рівність трикутників АВС і MKN.
| 5. Через точку В кола проведено діаметр, хорду та дотичну. За рисунком знайти більший з кутів між хордою і дотичною. | 
|
Високий рівень
1. Точки Х і Y розміщені по різні боки від прямої СD так, що ХС = YС, XD = YD. М — довільна точка відрізка СD. Довести, що відрізки ХМ і YМ рівні.
2. Дві сторони трикутника відносяться як 5 : 7, а третя сторона дорівнює їх півсумі. Знайти сторони трикутника, якщо його периметр дорівнює 36 см.
| 3. У колі проведено діаметр AB і дві хорди АN і ВМ так, що ÐВАN = ÐАВМ. Довести, що хорди AN і ВМ рівні. 4. У трикутнику MNK кут М дорівнює 76°, а кут K дорівнює 45°. Знайти градусну міру кута між бісектрисою і висотою трикутника, проведеними з вершини кута М. | 
|
5. Побудувати трикутник за двома сторонами, якщо відомо, що вершина, протилежна одній із заданих сторін, розміщена на відстані b від деякої заданої точки М.
Варіант 4
Початковий рівень
1. На промені ОВ позначена точка А. Відомо, що OВ = 27 см, ОА = 15 см. Знайти довжину відрізка АВ.
а)42 см; б)13,5 см; в ) 12 см; г)7,5 см.
2. Один із двох суміжних кутів дорівнює 50°. Знайти інший кут.
а)100°; б)25°; в)40°; г)130°.
3. Трикутник ACD дорівнює трикутнику MKP. Вказати правильну рівність.
а)CD = MP; б)AC = MK; в)ÐA = ÐP; г)ÐK = ÐC.
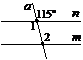4. Дано: m||n, а — січна. Знайти: Ð1 і Ð2.
а)115° і 115°; б)65° і 65°;
в)65° і 25°; г)115° і 65°.
5. Знайти периметр трикутника, сторони якого дорівнюють 7 см, 15 см, 9 см.
а)22 см; б)24 см; в)6 см; г)31 см.
6. Знайти третій кут трикутника, якщо два інші дорівнюють 75° і 25°.
а)100°; б)105°; в)155°; г)80°.
7. Два кола з радіусами 3 см і 11 см мають зовнішній дотик. Знайти відстань між центрами кіл.
а)22 см; б)14 см; в)6 см; г)8 см.
8. Діаметр CD кола перпендикулярний до хорди MN завдовжки 10 см. Знайти довжину відрізка MK. 
а)10 см; б)20 см;
в)5 см; г)15 см.
9. Дано: a||b, AB = 7 см, MN = 4 см, KP = 9 см. Відстань між паралельними прямими а і b дорівнює:
а)7 см; б)4 см;
в)не визначається; г)9 см.
10. Вказати правильне твердження.
а)Точка перетину бісектрис трикутника є центром кола, описаного навколо трикутника;
б)висота трикутника ділить його на два рівні трикутники;
в)катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині гіпотенузи;
г)якщо відповідні кути, що утворюються при перетині двох прямих третьою, рівні, то прямі паралельні.
Середній рівень
1. У трикутнику PMK сторони PM і MK відповідно дорівнюють 15 см і 11 см, а сторона PK утричі менша від сторони PM. Знайти периметр трикутника.
2. Один з гострих кутів прямокутного трикутника дорівнює 82°. Знайти інший гострий кут трикутника.
| 3. За рисунком вказати, яка зі сторін трикутника АСM дорівнює 7 см? | 
|
| 4. Чи будуть прямі m і n паралельні? |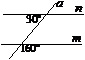 
|
Достатній рівень
1. У трикутнику АВС сторона АС дорівнює 10 см, а сторона АВ менша від сторони ВС на 7 см. Знайти невідомі сторони трикутника, якщо його периметр дорівнює 57 см.
2. У рівнобедреному трикутнику кут між бічними сторонами удвічі менший від кута при основі. Знайти кути трикутника.
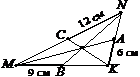3. У трикутнику MNK проведені медіани МА, NB, KС. Знайти периметр трикутника, якщо МВ = 9 см, АK = 6 см, NC = 12 см.
4. Довести рівність трикутників САD і МKР.
| 5. Через точку В кола проведено діаметр, хорду та дотичну. За рисунком знайти кут між хордою і діаметром. | 
|
Високий рівень
1. Точки М і N розміщені по різні боки від прямої АВ так, що МА = NА, МВ = NB. Довести, що медіани BC і BD трикутників ABM і ABN рівні.
2. Дві сторони трикутника відносяться як 3 : 5, а третя сторона дорівнює їх півсумі. Знайти сторони трикутника, якщо його периметр дорівнює 48 см.
3. У колі проведено діаметр АВ та паралельні хорди АN і ВМ. Довести, що хорди AN і ВМ рівні.
4. У трикутнику АВС кут А дорівнює 100°, кут В дорівнює 24°. Знайти градусну міру кута, між бісектрисою і висотою трикутника, проведеними з вершини С.
5. Побудувати трикутник за стороною, висотою, проведеною до цієї сторони, якщо відомо, що вершина, протилежна заданій стороні, розміщена на відстані bвід деякої заданої точки М.
ЗМІСТ
Дата добавления: 2018-05-12; просмотров: 2837; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!