Теплопровідність плоскої стінки при граничних умовах першого роду

Під плоскою стінкою розуміють таку стінку, в якій тепло проводиться тільки по товщині, а в двох інших напрямках, тобто по висоті і ширині тепловий потік незначний і їм можна нехтувати, тобто мова йде про одномірне температурне поле.

x

ᵟ

q

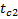
t

В загальному випадку, теплопровідність через плоску стінку описується рівнянням теплопровідності Фур'є:

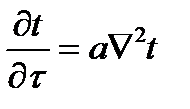
Для стаціонарного режиму:

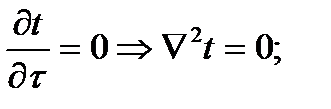
для плоскої стінки

Доповнимо це рівняння умовами однозначності:

1. Геометричні умови: δ=const;

2. Фізичні умови: λ=const;

3. Початкові умови;

4. Граничні умови: якщо x=0, то t=t₁; якщо x=δ,

5. то t=t₂. Звідси маємо, що t₁>t₂.

Отримали систему рівнянь, яка описує процес теплопровідності в плоских умовах:

                 

 

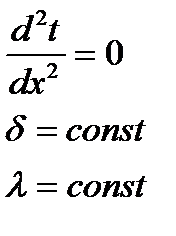
Треба знайти q, і t=f(x). Інтегруємо перше рівняння , дає 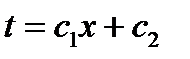 (де с₁ і с₂ константи), тоді аналізуючи це рівняння ми бачимо, що це рівняння впливу y=kx+b, це значить, що зміна температури в стінці змінюється по лінійному закону.

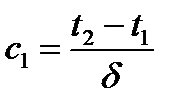, підставляючи в це рівняння

.

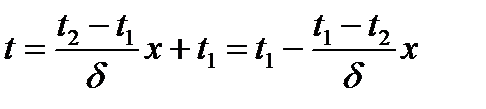Згідно рівняння Фур'є: 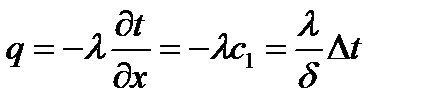, де Δt=t₁–t₂, або

,

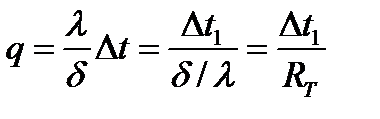де λ – провідність, δ/λ=R_T – термічний опір.

Густина теплового потоку пропорційна різниці температур і обернено порційна термічному опору стінки.

Теплопровідність багатошарової стінки

Стінка, яка складається з декількох шарів називається багатошаровою

При стаціонарному режимі, густина теплового потоку постійна і однакова для кожного із шарів.

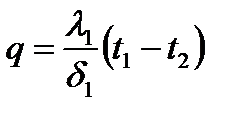
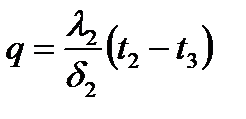
Перепишемо ці рівняння відносно температурних різниць:

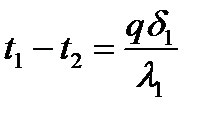
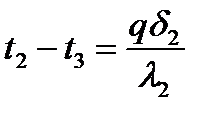
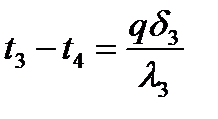
t1

Якщо всі три рівняння описують одне і те ж явище, то і четверте рівняння (сума цих) рівняння теж описуватиме всі ці явища

t4

t3

t2

λ3

λ2

λ1

q

ᵟ3

ᵟ2

ᵟᵟ1

λ

t

:

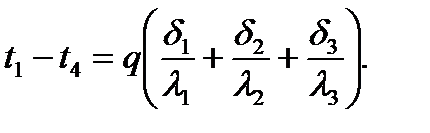
    Температури t₂ та t₃ можемо знайти:

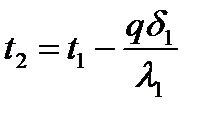
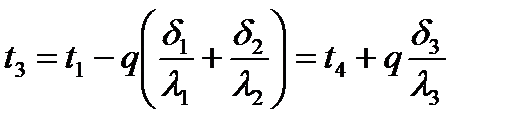
Теплопровідність плоскої стінки при граничних умовах третього роду

Нехай плоска стінка омивається із лівої сторони рідини із tp1 і інтенсивністю тепловіддачі α1, з другого боку омивається рідиною із температурою tp2 і інтенсивністю тепловіддачі α2. Оскільки густина теплового потоку величина постійна і однакова як з тепловіддачі з обох сторін, так і теплопровідності, то тоді можна записати q= α1(tp1 – t1) – кількість теплоти, яка передається від гарячої рідини до стінки, ця ж теплота передається через стінку:

;

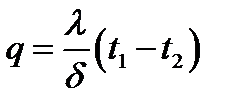q= α₂ (t₂ – t_р2) – кількість теплоти, що віддається другій рідині. Перепишемо ці рівняння відносно температур:

; ;

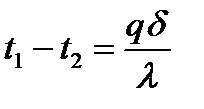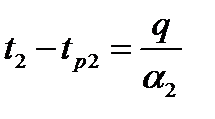
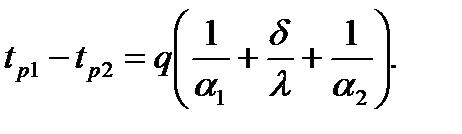
1/α₁ – термічний опір тепловіддачі від рідини до стінки. Якщо ми позначимо

, тоді q=k(tp₁ – tp₂), величину k – назвемо коефіцієнтом теплопередачі і тоді для теплової енергії ми можемо переписати рівняння наступним чином:

Qτ=kF(t_p1 – t_p2)τ                                                        [Дж]

Q=kF(t_p1 – t_p2)                                                           [Вт]

Це три різні форми запису основного рівняння теплопередачі. Формулювання: основне рівняння теплопередачі показує, що кількість теплоти, яка передається від одного теплоносія до іншого пропорційна поверхні, різниці температур між теплоносіями та часу.

Порядок знаходження коефіцієнту теплопередачі:

1) встановлюємо фізичну модель омивання стінки рідиною (режим течії рідини, вільна чи вимушена конвекція, обмежений чи необмежений простір);

2) знаходимо відповідне критеріальне рівняння. Наприклад, виду Nu=C*Re^m*Prⁿ, де Re=ω*d*ρ/μ, Pr=c*μ/λ. Якщо отримано Nu=100, то з виразу Nu=αl/λ отримуємо:

α= Nu*λ/l=100*λ/l.

Вирази для температур поверхонь стінки:

.

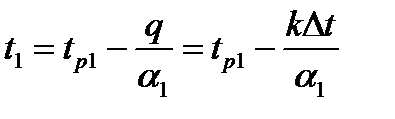
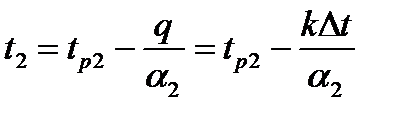Коефіцієнт k показує, яка кількість теплоти передається від одного теплоносія до іншого через стінку, що їх розділяє, площею 1 м2 при різниці температур між теплоносіями 1 0С в одиницю часу. В загальному випадку, для багатошарових стінок можна записати:

.

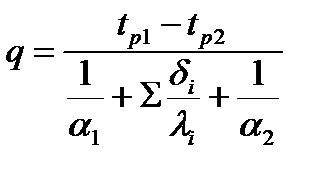В теплообмінниках при прямотоці має місце наступна графічна залежність температури:

Тут 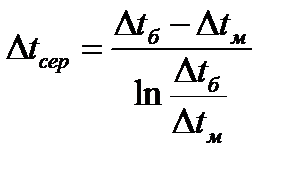 за диференціальним законом. Уточнене рівняння теплопровідності:

 

q=kΔt_сер. Для змінного току:

---

Дата добавления: 2018-05-09; просмотров: 414; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!