Нехай функція задана параметрично
Лекція 13 Елементи теорії лінійних просторів: лінійні оператори, власні вектори та власні числа, ортогональний оператор. Квадратичні форми та зведення їх до канонічного вигляду
1. Власні числа та власні вектори лінійних перетворень
Розглянемо лінійне перетворення

 ,
,  ,
,  ,
,
Y=AX. Вважаючи X і Y векторами з відповідними координатами, записане перетворення А тлумачимо як таке, що переводить вектор Х у вектор У за допомогою матриці А. Знайдемо вектор, який при даному перетворенні змінюється найменше, тобто переходить у колінеарний йому.
Власним вектором Х лінійного перетворення А називається ненульовий вектор, який задовольняє співвідношення:
 ,
,
при цьому  називається власним числом перетворення.
називається власним числом перетворення.
Маємо:
 ,
,
де 0 – нульова матриця відповідного розміру, або
 ,
,
де Е – одинична матриця відповідного розміру.
Отже,
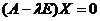 .
.
Реалізуємо останню рівність у випадку перетворення (1) та його матриць. Маємо:

 ,
,
або
 ,
,
тобто

Звідси знаходимо хі. Отримана одномірна система має ненульовий розв’язок тільки тоді, коли det(A-  E)=0, тобто
E)=0, тобто
 .
.
Описана процедура знаходження власних чисел та векторів для випадку трьох змінних переноситься й на випадок довільної скінченої кількості змінних.
2. Квадратична форма та зведення її до канонічного виду
|
|
|
Квадратичною формою кількох змінних називається многочлен, який містить тільки другі степені цих змінних та (чи) тільки їхні попарні добутки.
Для двох і трьох змінних маємо зокрема (деякі коефіцієнти подвоєно для зручності)
 ;
;
 .
.
Тут сталі аij одночасно не всі дорівнюють нулю.
Для більшого числа змінних квадратичні форми визначаються аналогічно.
Для квадратичної форми трьох змінних введемо позначення а12=а21, а13=а31, а23=а32.
Маємо
 .
.
Ввівши відповідні матриці, надамо останні рівності такого вигляду



 .
.
Отже, квадратична форма тепер набирає вигляду
 .
.
Розглянемо довільне лінійне перетворення, результатом якого є Х. Нехай X=BY. Тоді
 .
.
Отже,
 .
.
Позначивши ВТАВ=С, дістанемо F=YTCY, тобто вид квадратичної форми при лінійному перетворенні матриці Х. Оскільки
 ,
,
то матриця С у цьому випадку симетрична.
Під канонічним видом квадратичної форми розуміють такий, який містить тільки квадрати змінних.
Наведемо спосіб зведення квадратичної форми до канонічного виду.
Якщо деяку симетричну матрицю А (як у випадку матриці квадратичної форми) розглядати як матрицю відповідного лінійного перетворення в деякому прямокутному базисі, то можна знайти прямокутний базис, складений з власних векторів матриці А.
|
|
|
Як було зазначено вище, перехід від одного прямокутного базису до іншого здійснюється за допомогою ортогональної матриці, а після перетворення

в базисі з власних векторів матриця набирає діагонального виду. Для матриці квадратичної форми можна побудувати ортогональну матрицю В, для якої матриця (ВТ)-1АВТ буде діагональною з власними значеннями А по діагоналі.
Отже, матрицю квадратичної форми можна звести до діагонального виду в базисі з власних векторів.
На основі цього твердження можна спрощувати рівняння ліній (чи поверхонь) другого порядку. Справді, нехай маємо лінію другого порядку
 .
.
Тоді відповідну квадратичну форму
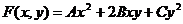
можна звести до канонічного виду
 ,
,
що істотно спрощує відповідне рівняння. Тут  і
і  - власні значення матриці квадратичної форми. Доведення цього факту опускаємо.
- власні значення матриці квадратичної форми. Доведення цього факту опускаємо.
Лекція 14 Поверхні другого порядку
Сфера – це множина точок простору, рівновіддалених від даної точки, яка називається центром.
Якщо М0(х0, у0, z0) – центр сфери, М(х, у, z) – її змінна точка, а відстань ММ0=R, то з рівності (ММ0)2=R2 дістаємо канонічне рівняння сфери:
|
|
|
 ,
,
Якщо центром сфери є точка М0(0, 0, 0), то маємо
 .
.
Це рівняння сфери найпростіше з канонічних рівнянь.
Перейдемо тепер до розгляду інших поверхонь. Задаватиме їх канонічними рівняннями, а для побудови образу відповідного рівняння застосуємо метод „поперечних перетинів”. Суть його полягає в тому, що форма поверхні визначається множиною ліній у просторі, отриманих в результаті перетину даної поверхні координатними площинами, а якщо треба, то множиною площин, паралельних координатним. У деяких випадках дослідження буде детальним, а в деяких дамо тільки остаточні результати. Вважатимемо, що всі параметри додатні.
Еліпсоїд – це поверхня, канонічне рівняння якої
 ,
,
де a, b, c називають півосями еліпсоїда.
Розглянемо перетини еліпсоїда площинами z=h, тобто

Звідси
 ,
,
де  ,
, 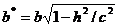 .
.
Якщо  , то останні рівняння – це рівняння еліпсів, які при
, то останні рівняння – це рівняння еліпсів, які при  вироджуються в точку.
вироджуються в точку.
Якщо  , то площини не перетинають поверхню.
, то площини не перетинають поверхню.
Аналогічно можна розглянути й перетини x=h, y=h і за множиною всіх перетинів встановити форму поверхні (рис. 14.1).
Подамо канонічні рівняння деяких алгебраїчних поверхонь другого порядку.
Одно порожнинний гіперболоїд (рис. 14.2)
|
|
|
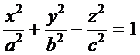 .
.
Двопорожнинний гіперболоїд (рис. 14.3)
 .
.
Еліптичний параболоїд (рис. 14.4)
 .
.
Гіперболічний параболоїд (рис. 14.7)
 .
.
Конус (рис. 14.5)
 .
.



Рисунок 14.1 Рисунок 14.2 Рисунок 14.3



Рисунок 14.4 Рисунок 14.5 Рисунок 14.6

Рисунок 14.7
Рівняння виду F(x, y) = 0, розглянуті в R3, задають циліндричні поверхні, причому рівняння F(x, y) = 0 на площині визначає напрямну поверхні, твірні якої паралельні осі Оz. Наприклад, еліптичний циліндр (рис. 14.6)
 , (x, y)
, (x, y)  R3.
R3.
Не тільки циліндричні та конічні поверхні можна утворити за допомогою відповідного зміщення лінійних твірних. Це ж стосується й одно порожнинного гіперболоїда і гіперболічного параболоїда.
Очевидно будь-яка пряма L

лежить на гіперболічному параболоїді
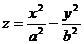 ,
,
оскільки кожна точка L задовольняє останнє рівняння. Помінявши знаки перед y у рівняннях L, можна дістати ще одну сім’ю ліній, що лежать на заданому параболоїді.
Поверхні, які мають такі властивості, називають лінійчатими. Лінійчаті поверхні, таким чином, конструюються з прямолінійних рейок. Цю властивість поверхонь використовують при конструюванні різних перекриттів, опор. Такі конструкції називають конструкціями Шухова (на честь відомого російського інженера). Це – покрівлі вокзалів, цирків, ринків, опори водогінних башт, антенних пристроїв тощо.
Модуль 5 Застосування похідної та інтегралу. Диференціальні рівняння. Ряди
Лекція 15 Похідна складної функції, функції заданої неявно, параметрично, аналітично. Використання похідної при розв’язанні оптимізаційних задач
1. Похідна функції. Диференціювання функції заданих неявно та параметрично
Похідною функції у=f(х) в точці х називається границя (якщо вона
існує) відношення приросту функції  до приросту аргументу
до приросту аргументу  , коли приріст аргументу прямує до нуля, тобто
, коли приріст аргументу прямує до нуля, тобто
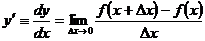 .
.
Функція, яка має скінчену похідну в точці х, називається диференційованою в цій точці. Знаходження похідної у' називається диференціюванням.
Основні правила диференціювання:
1.  4.
4. 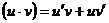
2.  5.
5. 
3. 
Диференціювання функції заданої параметрично.
Нехай функція задана параметрично

При чому  диференційовані при певних t, а
диференційовані при певних t, а  має обернену функцію. Тоді похідна від функції y по змінній x находиться за формулою
має обернену функцію. Тоді похідна від функції y по змінній x находиться за формулою
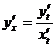
Дата добавления: 2018-05-09; просмотров: 256; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
