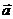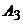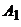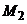ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
Nbsp;
Задачи на плоскость и прямую в пространстве
Цель настоящих методических указаний заключается в том, чтобы представить набор типовых задач по следующим разделам аналитической геометрии: «Плоскость», «Прямая в пространстве», «Плоскость и прямая». Предложенный набор упражнений ориентирован на освоение ключевых теоретических понятий и утверждений посредством приобретения практических навыков решения стандартных задач по курсу. При этом не требуется применения каких-либо нетрадиционных приемов или теоретических утверждений, выходящих за рамки курса.
ПЛОСКОСТЬ
Основные сведения из теории
В декартовой системе координат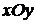 
плоскость 
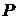может быть задана уравнением одного из следующих видов.
1. Общее уравнение плоскости:
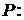
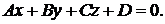
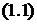
Вектор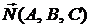 
перпендикулярен плоскости.
2. Уравнение плоскости, проходящей через заданную точку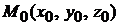 
перпендикулярно нормальному вектору 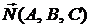, имеет вид
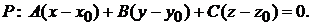(1.2)
3. Уравнение плоскости в отрезках на осях:
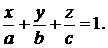(1.3)
Здесь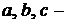 
величины направленных отрезков, отсекаемых плоскостью на координатных осях 
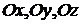соответственно, т. е. плоскость проходит через три точки: 
, 
, 
.
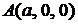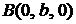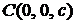Кроме того, понадобятся следующие формулы, доказательство которых можно найти в теоретическом курсе. 
4. Угол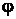 
между двумя плоскостями
|
|
|
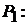
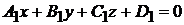
и
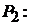
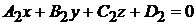
равен углу между нормальными векторами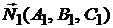 
и 
:
; 
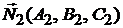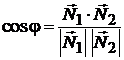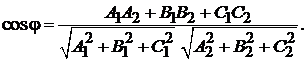(1.4)
Плоскости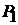 
и 
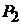параллельны тогда и только тогда, когда векторы 
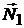и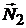 
коллинеарны ( 
):
.
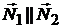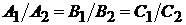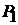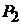Плоскости и перпендикулярны тогда и только тогда, когда векторы 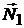и 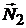ортогональны (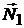 
):
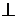
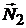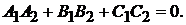
5. Расстояние от точки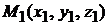 
до плоскости : 
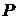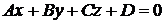равно
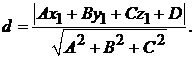(1.5)
6. Уравнение плоскости, проходящей через линию пересечения двух плоскостей
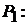
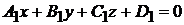
и
,
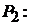
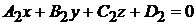следует искать в виде
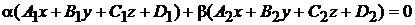, (1.6)
где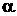 
и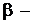 
некоторые числа.
Множество плоскостей, проходящих через линию пересечения двух заданных плоскостей, называется пучком плоскостей.
Решение типовых задач
Задача 1.1.Составить уравнение плоскости, проходящей через точку
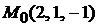, если задан нормальный вектор 
.
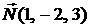Решение. Воспользуемся уравнением (1.2):
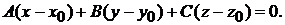
Подставляя координаты вектора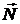 
и точки 
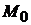, получим
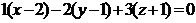
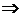
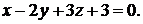
Ответ: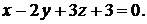 
Задача 1.2.Составить уравнение плоскости, проходящей через точку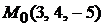 
параллельно векторам 
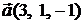и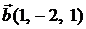 
(их называют направляющими векторами плоскости).
Решение.
Первый способ. Пусть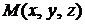 
– произвольная точка на плоскости. Тогда векторы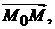 
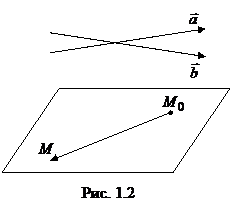
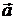и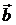 
(рис. 1.2) должны быть компланарны, т. е. их смешанное произведение должно быть равно 0: 
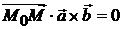. Запишем смешанное произведение через координаты векторов. Получим
|
|
|
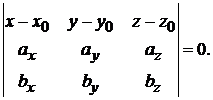
Подставим заданные координаты и вычислим определитель разложением по элементам первой строки:
,
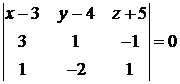или
.
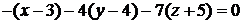Окончательно: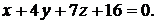 
Второй способ. Найдем сначала вектор 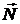(рис. 1.1). Очевидно, что вектор нормали 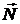к плоскости должен быть ортогонален также векторам 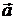и 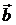. Поэтому его можно выбрать как векторное произведение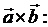 
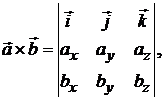
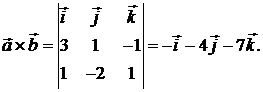
Затем выпишем общее уравнение плоскости, используя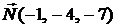 
, 
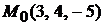(см. формулу (1.2)). Получим
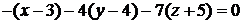
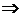
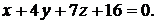
Ответ: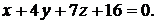
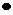Полезная формула. Если плоскость проходит через точку 
, 
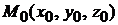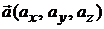и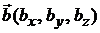 
– ее направляющие векторы, то уравнение плоскости имеет вид
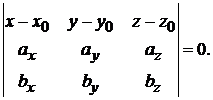(1.7)
Замечание. Первый способ решения задачи предпочтительнее. Второй способ отличается лишь тем, что в нем смешанное произведение трех векторов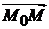 
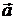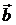, , вычисляется последовательно. А именно: сначала находим векторное произведение 
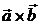и затем результат умножаем скалярно на вектор 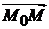. В дальнейшем при решении задач будем придерживаться первого способа.
Задача 1.3.Составить уравнение плоскости, проходящей через точки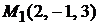 
и 
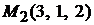параллельно вектору 
.
|
|
|
|
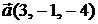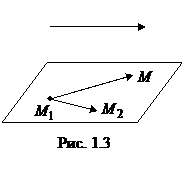Решение. Пусть 
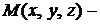произвольная точка на плоскости. Тогда векторы 
, 
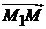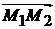и 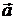компланарны (рис. 1.3). Запишем условие компланарности векторов через их координаты:
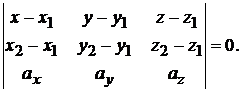
Подставляя заданные координаты, получим
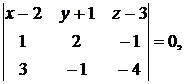
или
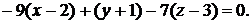
Окончательно: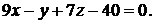 
Ответ: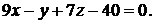
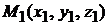Полезная формула. Если плоскость проходит через две заданные точки и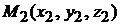 
параллельно вектору 
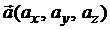, то ее уравнение имеет вид
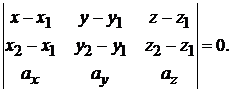(1.8)
Задача 1.4.Составить уравнение плоскости, проходящей через точку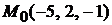 
параллельно плоскости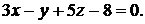 
Решение. В качестве вектора 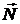искомой плоскости можно выбрать нормальный вектор заданной плоскости, так как эти плоскости параллельны. Таким образом, имеем 
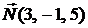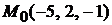и . Подставляя координаты 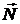и 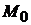в уравнение (1.2), получим
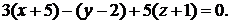
Окончательно: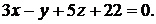 
Ответ: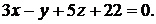
Задача 1.5.Найти величину острого угла между плоскостям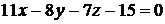и 
и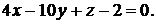 
Решение. Угол между плоскостями равен углу между нормальными векторам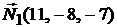и 
и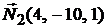 
(см. формулу 1.4)).
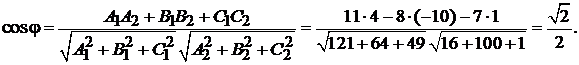
Отсюда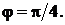 
Ответ: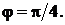
Задача 1.6.Чему равен угол между плоскостям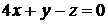и 
и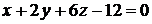 
?
Решение. Найдем скалярное произведение нормальных векторов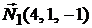 
и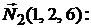 
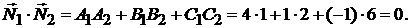
Следовательно, эти плоскости перпендикулярны: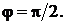 
Ответ: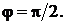
Задача 1.7.Составить уравнение плоскостей, которые проходят через точку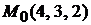 
и отсекают на координатных осях отличные от нуля отрезки одинаковой длины.
|
|
|
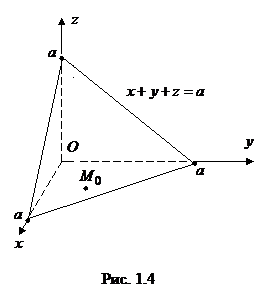Решение. Воспользуемся уравнением плоскости в отрезках на осях (1.3). Рассмотрим сначала случай 1: 
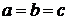(рис. 1.4). Тогда получим
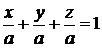
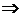
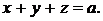
Подставляя в уравнение координаты точки 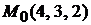, найдем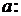 
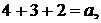
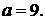
Уравнение плоскости: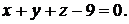 
Затем следует аналогично рассмотреть случаи 2: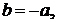 
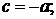3: 
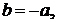
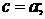4: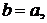 
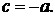Получим четыре различные плоскости.
Ответ: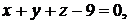 
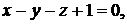
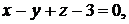
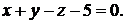
Задача 1.8.Построить плоскости, заданные уравнениями: 1)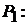 
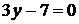; 2) 
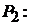
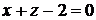; 3) 
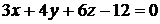; 4) плоскость 
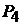, проходящую через точку 
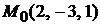параллельно плоскости 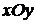; 5) плоскость 
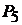, проходящую через точку 
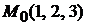и ось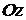 
.
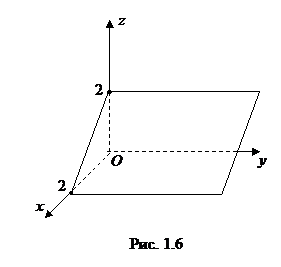
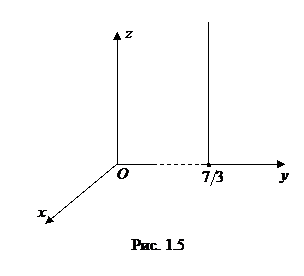Решение. 1. Плоскость 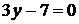параллельна плоскости 
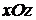и отсекает на оси 
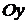отрезок, равный 
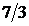(рис. 1.5).
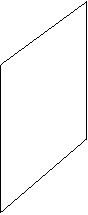
2. Плоскость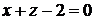 
параллельна оси 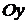, пересекает плоскость 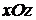по прямой 
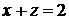, отсекая на осях 
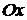и 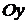отрезки, равные 2 (рис. 1.6).
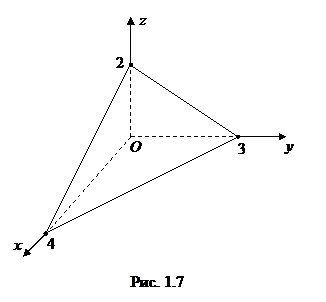
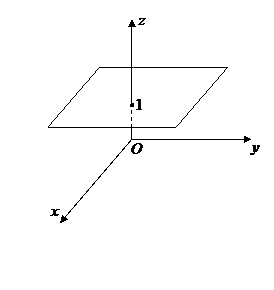3. Уравнение плоскости запишем в отрезках на осях (1.3): 
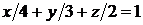. Плоскость отсекает на осях , , 
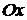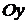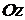отрезки, длины которых равны соответственно 4, 3, 2 (рис. 1.7).
|
4. Так как плоскость 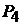параллельна плоскости 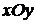, то ее нормальный вектор можно выбрать в виде 
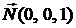. Тогда согласно формуле (1.2) уравнение плоскости 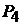будет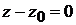 
, где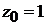 
по условию задачи. Таким образом, получаем 
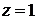(рис. 1.8).
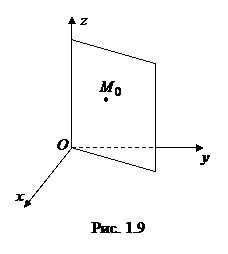5. Плоскость 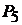проходит через ось 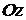. Поэтому ее нормальный вектор имеет вид 
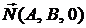. Так как плоскость проходит через начало координат 
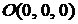, то коэффициент 
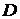в уравнении плоскости (1.1) равен 0. Подставляя координаты точки 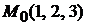в уравнение 
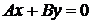, получаем 
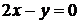(рис. 1.9).
Задача 1.9.Составить уравнение плоскости, проходящей через три заданные точки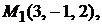 
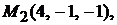
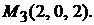
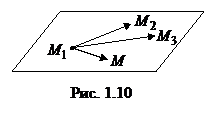Решение. Пусть 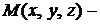произвольная точка на плоскости. Тогда векторы , , 
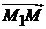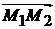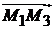компланарны (рис. 1.10). Запишем условие компланарности этих векторов через их координаты:
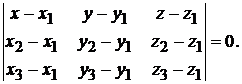
Подставим значения координат и найдем уравнение плоскости:
или
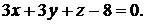
Ответ: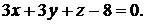
Полезная формула. Если плоскость проходит через три заданные точки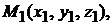 
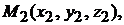
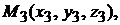не лежащие на одной прямой, то ее уравнение имеет вид
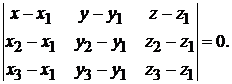(1.9)
Задача 1.10.Даны координаты вершин тетраэдра: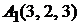 
, 
, 
, 
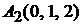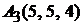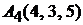(рис. 1.11). Составить уравнения его граней.
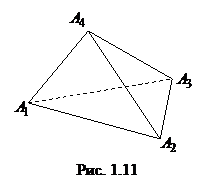Решение. Найдем уравнение грани 
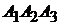. Для этого подставим в формулу (1.9) координаты вершин 
:
,
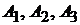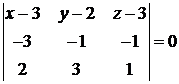или
.
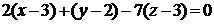Уравнение искомой грани имеет вид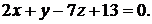 
Уравнения граней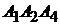 
, 
, 
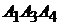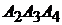найдите самостоятельно.
Ответ: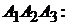 
.
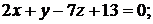
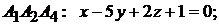
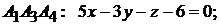
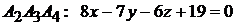Задача 1.11.Найти расстояние от точки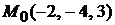 
до плоскости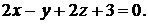 
Решение. Используем формулу (1.5):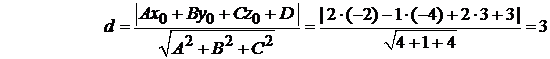 
.
Ответ: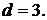 
Задача 1.12. Найти расстояние между параллельными плоскостями
.
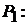
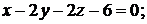
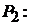
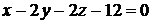Решение.
Первый способ. Выберем произвольно точку 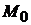на плоскости 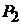. Пусть, например, 
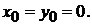Тогда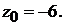 
Следовательно, 
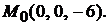Найдем расстояние 
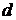от точки 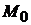до плоскости 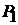, по формуле (1.5):
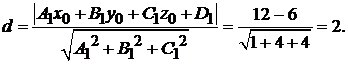
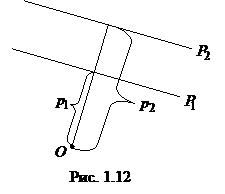Второй способ. Очевидно, что плоскост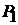и и 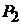лежат по одну сторону относительно начала координат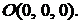 
Обозначим через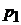 
расстояние от начала координат до плоскости 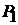, через 
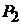– до плоскости (рис. 1.12).
, 
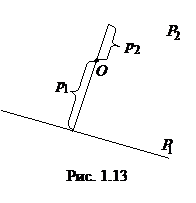
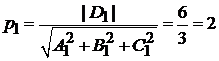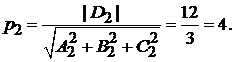
Расстояние между плоскостями равно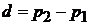 
. Отсюда находим
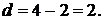
Ответ: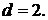 
Замечание. Если бы плоскости находились по разные стороны от начала координат (рис. 1.13), то расстояние между ними было бы равно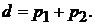 
ПРЯМАЯ В ПРОСТРАНСТВЕ
Основные сведения из теории
Прямая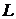 
в пространстве может быть задана уравнением одного из следующих видов.
1. Общие уравнения прямой:
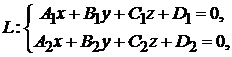(2.1)
где коэффициенты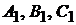 
не пропорциональны коэффициентам 
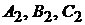. Это равносильно заданию прямой как линии пересечения двух плоскостей.
2. Параметрические уравнения прямой:
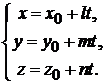(2.2)
Здесь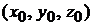 
– координаты какой-либо точки 
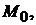принадлежащей прямой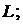 
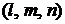– координаты вектора 
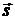, параллельного прямой. Вектор 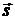называется направляющим вектором прямой. Переменная 
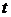– параметр,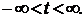 
3. Канонические уравнения прямой:
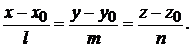(2.3)
4. Уравнения прямой, проходящей через две заданные точки 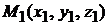и :
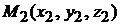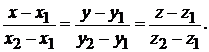(2.4)
Кроме того, при решении задач будут использоваться следующие формулы, доказательство которых можно найти в теоретическом курсе.
5. Угол 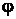между двумя прямыми
; 
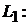
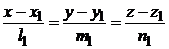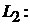
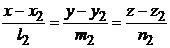
равен углу между направляющими векторами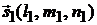 
и 
:
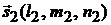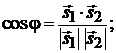
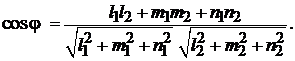(2.5)
Прямые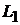 
и 
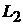параллельны тогда и только тогда, когда векторы 
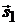и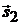 
коллинеарны ( 
):
.
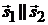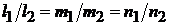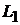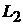Прямые и перпендикулярны тогда и только тогда, когда векторы 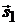и 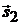ортогональны ( 
):
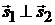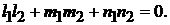
Решение типовых задач
Задача 2.1.Найти канонические уравнения прямой, заданной как линия пересечения двух плоскостей: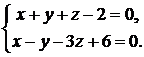 
Решение. Прямая задана общими уравнениями (2.1). Найдем какую-нибудь точку 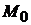на прямой. Выберем, например, 
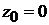. Другие координаты получим из системы уравнений 
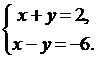Очевидно, что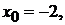 
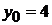. Следовательно, 
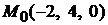. Затем находим направляющий вектор 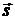прямой. Так как прямая принадлежит одновременно обеим плоскостям, то вектор 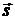ортогонален нормальным векторам этих плоскостей, т. е.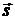 
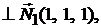
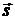
(рис. 2.1). Поэтому за направляющий вектор 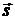можно принять
.
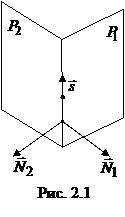
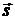
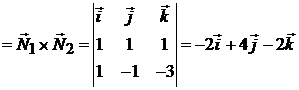Подставляя координаты направляющего вектора 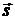и точки 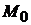в уравнения прямой (2.3), получим
.
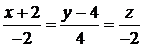
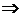
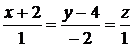Ответ: .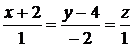
Полезная формула. Если прямая задана как линия пересечения двух плоскостей:
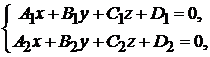
то ее направляющий вектор 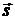можно выбрать в виде
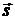
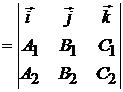. (2.6)
Задача 2.2.Найти параметрические и канонические уравнения прямой, проходящей через точку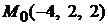 
и параллельной вектору 
.
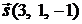Решение. Известны точка 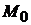и направляющий вектор 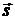прямой.
Согласно формуле (2.2) параметрические уравнения прямой имеют вид
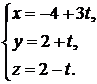
Канонические уравнения получаем, используя формулу (2.3):
.
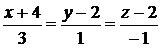Ответ: .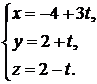
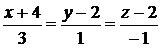Задача 2.3.Найти направляющий вектор прямой :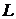 
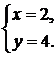
Решение. Прямая 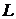проходит через точку 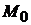(2, 4) на плоскости 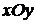и параллельна оси 
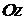(рис. 2.2). Очевидно, что ее направляющий вектор можно выбрать в виде 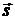(0, 0, 1).
Ответ: 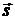(0, 0, 1).
.
Задача 2.5.Найти косинус острого угла между прямыми
: 
; 
: 
.
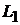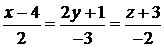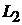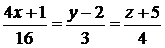Решение. Из уравнений прямых вытекает, что направляющий вектор прямой 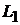равен 
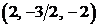, направляющий вектор прямой 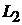равен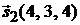 
. Для удобства вычислений направляющий вектор прямой 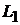выберем в виде 
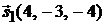. Он коллинеарен исходному. Используя формулу (2.5), получаем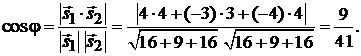 
Ответ: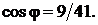 
Задача 2.6.Показать, что прямая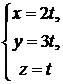 
перпендикулярна прямой
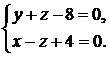
Решение. Направляющий вектор первой прямой, очевидно, равен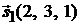 
, направляющий вектор второй прямой 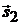найдем с помощью формулы (2.6):
.
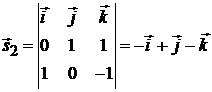Вычислим скалярное произведение векторов 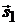и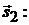 
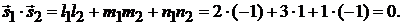
Ответ: прямые перпендикулярны.
Задача 2.7.Проверить, лежат ли три данные точк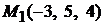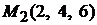и 
, 
и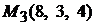 
на одной прямой.
Решение. Напишем уравнения прямой, проходящей через две заданные точк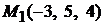и и 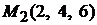, согласно формуле (2.4). Получим
.
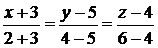
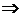
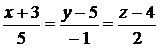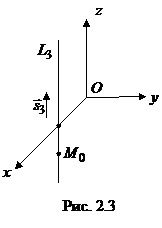Проверим, удовлетворяют ли координаты точки 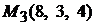этим уравнениям. После подстановки 
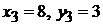получаем: 
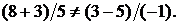Следовательно, точка 
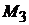не лежит на прямой.
Ответ: не лежат.
Задача 2.8.Найти канонические уравнения прямых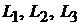 
, проходящих через точку 
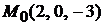параллельно: 1) оси 
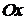; 2) оси 
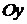; 3) оси .
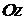Решение. Найдем уравнения прямой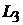 
, проходящей через точку 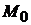параллельно оси 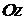. Ее направляющий вектор 
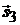можно выбрать в виде 
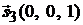(рис. 2.3).
Используя формулу (2.3), получим
: 
.
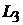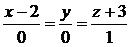Таким же образом находим 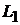и .
: 
, 
;
: 
, 
.
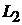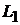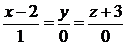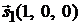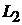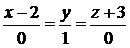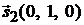Ответ: :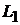 
; : 
; : 
.
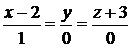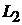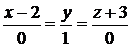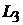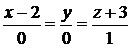Задача 2.9.Найти точки пересечения прямой :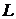 
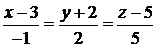с плоскостями координат.
Решение. Для того чтобы найти точку пересечения прямой 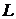с плоскостью 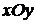, в канонических уравнениях прямой 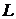следует положить 
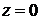. Получим 
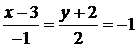, откуда 
, 
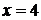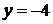. Таким образом, прямая 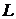пересекает плоскость 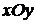в точке 
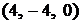. Аналогично находим точки пересечения с плоскостям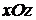и и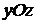 
.
Ответ: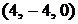 
; 
; 
.
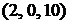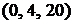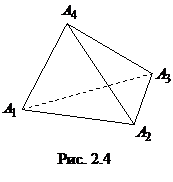Задача 2.10.Известны координаты вершин тетраэдра: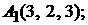 
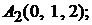
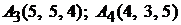. Составить канонические уравнения его ребер и найти их длины.
Решение. Условие такое же, как и в задаче 1.10 (рис. 2.4). Найдем уравнения ребра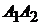 
. Для этого подставим координаты вершин 
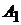и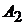 
в формулу (2.4). Получим 
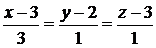. Теперь можно определить длину ребра :
.
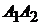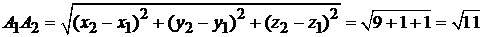Уравнения и длины остальных ребер найдите самостоятельно.
Ответ: 1) : ,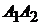 
;
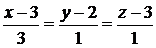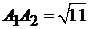2) 
: 
, 
;
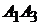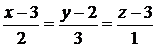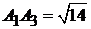3) 
: 
, 
;
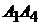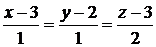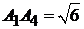4) 
: 
, 
;
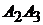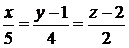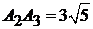5) 
: 
, 
;
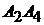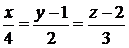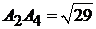6) 
: 
, 
.
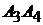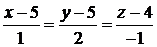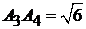Задача 2.11.Найти точку пересечения двух прямых
: 
: 
.
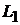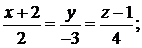
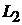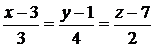Решение. Перепишем уравнения прямых в параметрическом виде
: 
: 
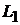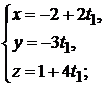
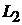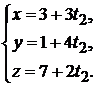
Для нахождения точки пересечения этих прямых нужно решить систему уравнений:
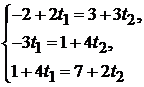
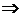
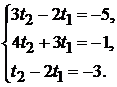
Очевидно, она имеет единственное решение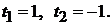 
Подставляя значение параметра 
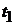в параметрические уравнения прямо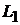й (или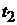 
в уравнения прямой 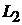), получим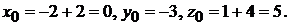 
Ответ: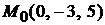 
.
ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
Основные сведения из теории
Пусть прямая задана каноническими уравнениями
: 
,
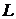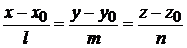а плоскость – общим уравнением
: 
.
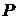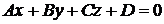1. Угол между прямой и плоскостью равен углу между направляющим вектором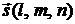 
прямой и нормальным вектором 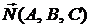плоскости и вычисляется по формуле
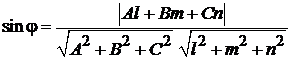. (3.1)
2. Условие параллельности прямой и плоскости имеет вид
.
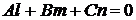Оно равносильно условию ортогональности векторов 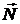и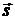 
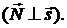
3. Условие перпендикулярности прямой и плоскости имеет вид
.
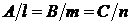Оно равносильно условию коллинеарности векторов 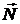и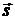 
.
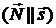4. Условие принадлежности прямой 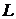плоскости 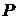записывается в виде
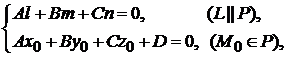(3.2)
где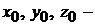 
координаты точки 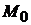, принадлежащей прямой.
Решение типовых задач
Задача 3.1.Найти острый угол между прямой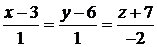 
и плоскостью 
.
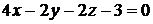Решение. Направляющий вектор прямой равен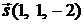 
. Нормальный вектор плоскости равен 
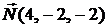. По формуле (3.1)
, 
.
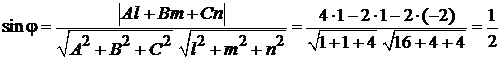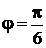Ответ: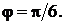 
Задача 3.2.При каком значении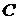 
прямая : 
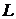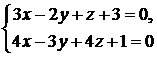параллельна плоскости : 
?
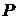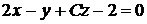Решение. Согласно условию задачи прямая 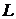задана как линия пересечения двух плоскостей. Нормальный вектор первой плоскости равен 
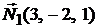, нормальный вектор второй плоскости равен 
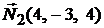. Направляющий вектор прямой равен 
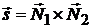(см. формулу (2.6)):
.
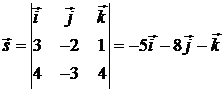Условие параллельности прямой 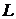и плоскости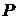 
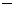это условие ортогональности направляющего вектора прямой 
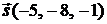и нормального вектора плоскости 
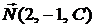, т. е. 
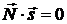. Умножая, получаем
.
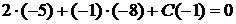
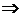
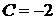Таким образом, уравнение плоскости будет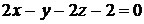 
.
Ответ: 
Задача 3.3.При каких значениях 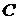и 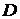прямая 
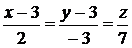лежит в плоскости 
?
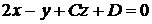Решение. Прямая будет параллельна плоскости, если ее направляющий вектор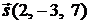 
будет ортогонален нормальному вектору плоскости 
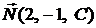, т. е. 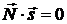. Запишем это условие:
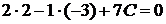
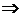
Прямая будет принадлежать плоскости, если координаты точки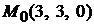 
, через которую проходит прямая, удовлетворяют уравнению плоскости: 
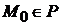. Отсюда получаем, что
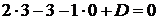
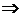
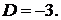
При решении задачи мы воспользовались формулой (3.2).
Ответ: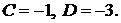 
Задача 3.4.Найти точку пересечения прямой :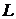 
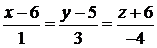и плоскости : 
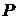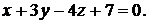
Решение. Запишем уравнения прямой в параметрическом виде
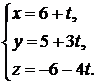
Подставляя выражения для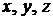 
в уравнение плоскости 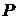, получим
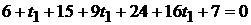
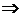
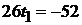
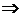
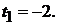
Теперь следует подставить значение параметра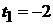 
в параметрические уравнения прямой 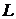. Находим 
.
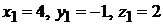Ответ: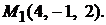 
Полезная формула. Если прямая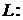 
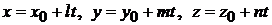пересекается с плоскостью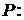 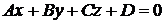, то точке пересечения 
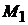отвечает значение параметра
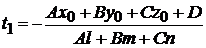. (3.3)
Задача 3.5.Найти уравнение плоскости 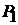, проходящей через прямую : 
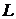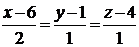перпендикулярно плоскости : 
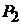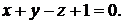
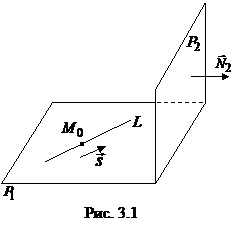Решение. Плоскость 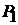имеет два направляющих вектора 
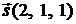и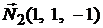 
и проходит через точку 
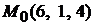(рис. 3.1). Согласно формуле (1.9) ее уравнение будет иметь вид
,
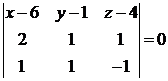или
.
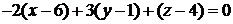Окончательно: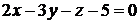 
.
Ответ: .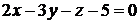
Задача 3.6.Известны координаты вершин тетраэдра: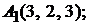 
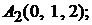
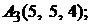
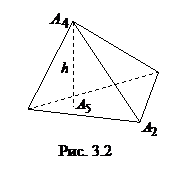
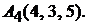Найти уравнение и длину его высоты 
.
|
|
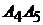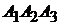имеет вид 
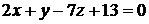. В качестве направляющего вектора 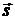высоты 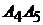можно выбрать нормальный вектор грани 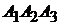, т. е. 
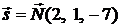(рис. 3.2). Кроме того, нам известны координаты точки 
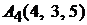, через которую проходит высота. Воспользуемся каноническими уравнениями прямой (2.3). Тогда получим
: 
.
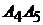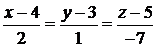Высоту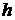 
можно найти по формуле (1.5), определяющей расстояние от точки 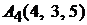до грани : .
.
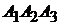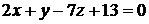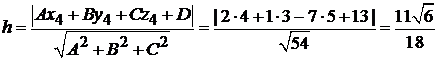(Напомним, что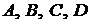 
– это коэффициенты в общем уравнении плоскости 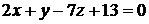, и они равны 
, 
, 
, 
.)
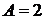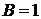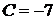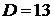Ответ: : ;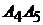 
.
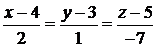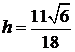Задача 3.7.Даны прямые :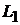 
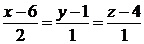и :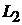 
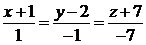. Найти уравнение плоскости 
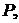проходящей через прямую 
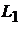параллельно прямой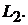 
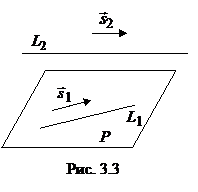
Решение. Векторы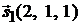 
и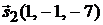 
являются направляющими векторами плоскости 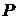(рис. 3.3). Точка 
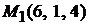принадлежит плоскости 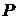. Решаем задачу, используя формулу (1.9):
,
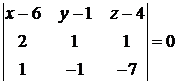или
.
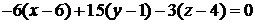Окончательно: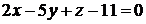 
.
Ответ: .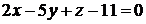
Задача 3.8.Составить уравнение плоскости, проходящей через прямую :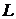 
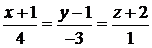и точку 
.
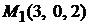Решение. Прямая 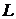проходит через точку 
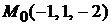и ее направляющий вектор равен 
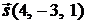. Произвольная точка 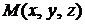будет принадлежать искомой плоскости 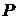, если векторы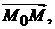 
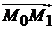и 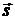компланарны: 
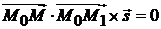(рис. 3.4), т. е.
.
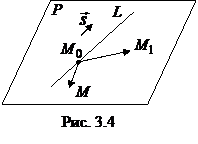
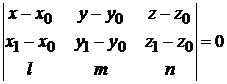Это и есть уравнение плоскости 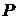. Подставляем координаты:
,
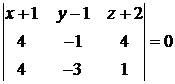или
.
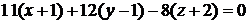Окончательно: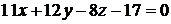 
.
Ответ: .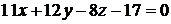
Полезная формула. Уравнение плоскости, проходящей через прямую 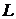: 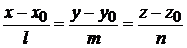и точку 
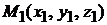, не лежащую на этой прямой, имеет вид
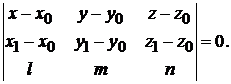(3.4)
Задача 3.9.Доказать, что прямые
: 
: 
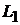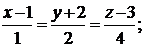
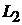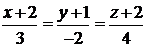
лежат в одной плоскости и найти уравнение этой плоскости.
Решение. Первая прямая проходит через точку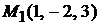 
и ее направляющий вектор 
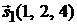. Вторая прямая проходит через точку 
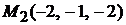и ее направляющим вектором является 
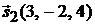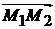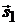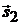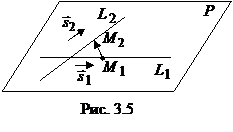
. Очевидно, что прямые лежат в одной плоскости, если векторы , и компланарны: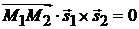 
(рис. 3.5), т. е.
.
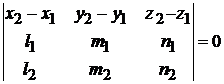Подставим заданные координаты:
.
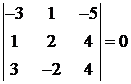Это означает, что прямые 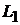и 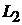лежат в одной плоскости. Векторы 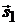и 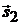не коллинеарны. Следовательно, эти прямые пересекаются.
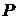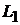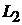Найдем уравнение плоскости , в которой лежат прямые и . Очевидно, что произвольная точка 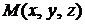будет принадлежать плоскости, если векторы 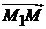, , 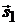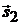компланарны: 
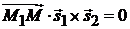(рис. 3.6), т. е.
.
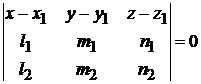Это и есть уравнение искомой плоскости. Подставляем координаты и вычисляем определитель разложением по элементам первой строки. Получаем
,
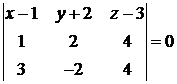или
.
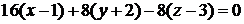Окончательно: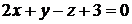 
.
Ответ: .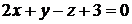
Полезные формулы. Две прямые
: 
: 
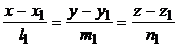
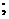
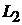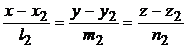
лежат в одной плоскости, если
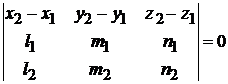. (3.5)
Если прямые пересекаются, то уравнением этой плоскости будет
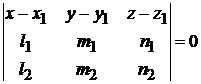. (3.6)
Замечание. Прямые скрещиваются (т. е. не лежат в одной плоскости) тогда и только тогда, когда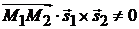 
и равенство (3.5) несправедливо.
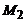Задача 3.10.Найти уравнение плоскости, проходящей через две параллельные прямые:
: 
: 
.
|
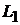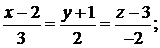
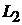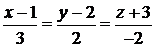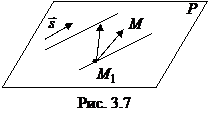
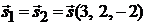. Первая прямая проходит через точку 
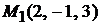, вторая 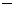через точку 
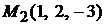. Произвольная точка 
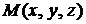принадлежит искомой плоскости 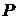, если векторы 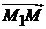, 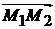и 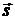компланарны: 
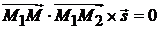(рис. 3.7), т. е.
.
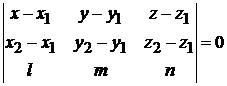Подставляя заданные координаты, находим уравнение плоскости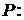
,
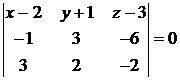или
.
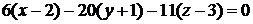Окончательно: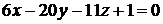 
.
Ответ: .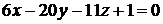
Полезная формула. Уравнение плоскости, проходящей через две параллельные прямые (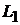 
, 
)
: 
: 
,
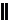
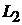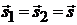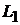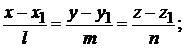
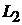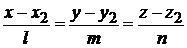имеет вид
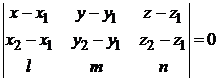. (3.7)
Замечание. В задачах 1.3, 1.9, 3.5, 3.8–3.10 без труда можно указать два направляющих вектора искомых плоскостей. Поэтому решение этих задач аналогично решению задачи 1.2. Если эти направляющие векторы явно не обозначены в ходе решения, то найдите их самостоятельно. Подумайте, что общего в формулах (1.7)–(1.9), (3.4)–(3.7).
Дата добавления: 2018-05-02; просмотров: 1253; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!