Нелинейная модель двухфакторного дисперсионного анализа

ВВЕДЕНИЕ

Широкое использование разнообразных экспериментальных методов исследований на современном этапе развития науки и техники требует от исследователей умения грамотно поставить, спланировать и провести эксперимент, а затем таким образом обработать полученные результаты, чтобы получить максимум информации об изучаемом явлении, объекте, веществе и т.п. Этого можно добиться только обладая определенными знаниями в области эксперимента. В связи с этим в последние годы в вузах страны вводится дисциплина “Обработка и анализ числовой информации”.

На современном этапе развития литейного производства существенные изменения претерпел методологический, технический и аппаратурный арсенал средств научных исследований. Это будет продолжаться и последующее время. Поэтому необходима своевременная ориентация и специализация подготовки студентов к будущей научной деятельности с учетом перспективных изменений, математизации и совершенствования методов и средств проведения и обработки результатов экспериментальных исследований.

1. ЦЕЛИ И ЗАДАЧИ КУРСА “ОБРАБОТКА И АНАЛИЗ ЧИСЛОВОЙ ИНФОРМАЦИИ”

Целью курса “Обработка и анализ числовой информации” является овладение студентами знаниями для грамотного планирования и проведения эксперимента и обработке его результатов с максимальной достоверностью. Основными задачами курса являются:

- знакомство с понятием “эксперимент” и его разновидностями;

- овладение методами первичной и вторичной обработок результатов эксперимента;

- использование методов математической статистики при проведении и обработке результатов эксперимента.

2. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Случайной величиной называется такая величина, которая с некоторой вероятностью может иметь то или иное значение в определенном диапазоне, заранее неизвестно какое.

Различают противные (дискретные) и непрерывные случайные величины. Дискретная случайная величина - такая случайная величина, которая принимает конечное или счетное множество различных значений. Такие значения являются изолированными, т.е. отдельными друг от друга.

Пример. Дискретными являются такие случайные величины, как число бракованных отливок в выборке из десяти изделий, X = {0, 1, 2,.....5,.....10}; число поломок формовочной машины в течение заданного срока эксплуатации и т.д.

Непрерывная случайная величина - это такая случайная величина, которая принимает любые значения на некотором интервале действительной числовой оси. Значения непрерывной случайной величины могут заполнять конечный или бесконечный интервал числовой оси. Число возможных значений непрерывной случайной величины всегда бесконечно.

Пример. Время безотказной работы отливки, испытуемой в течение 1000 часов, есть непрерывная случайная величина Х ={0 < х < 1000}; диаметр вала является непрерывной случайной величиной, понимающей любые значения на числовой оси: X={- < x < + }, а для годных валов значения ее ограничены полем допуска: Х={ 27,99 ≤ х ≤ 28,11}.

Непрерывными случайными величинами являются любые ошибки наблюдений или измерений, например, ошибка взвешивания, определение линейно-угловых размеров и т.п.

Дискретные и непрерывные случайные величины не следует противопоставлять друг другу. Наоборот, дискретная случайная величина является частным случаем непрерывной случайной величины.

В теории вероятности для общей характеристики случайной величины используют параметры, называемые числовыми характеристиками. Наиболее часто применяются следующие: среднее арифметическое, математическое ожидание, дисперсия, среднее квадратичное отклонение.

Среднее арифметическое.

. (2.1)

Математические ожидание М(х) - число, равное произведению всех возможных значений случайной величины на вероятности этих значений:

. (2.2)

Математическое ожидание приближенно равно среднему арифметическое значений случайной величины. Если производится несколько, серий опытов, то среднее арифметическое наблюдаемых в каждой серии значений случайной величины колеблется около М(х). Причем, с увеличением числа опытов в серии колебания уменьшаются, и средние арифметические приближаются к постоянной величине М(х).

Свойства математического ожидания:

- математическое ожидание постоянной величины равно самой постоянной:

М(с) = с; (2.3)

- постоянный множитель можно выносить за знак математического ожидания:

М(сx) = с М(x); (2.4)

- математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

М(x+y)= М(x)+ М(y); (2.5)

- математическое ожидание двух независимых случайных величин равно произведении их математических ожиданий:

М(xy)= М(x) М(y); (2.6)

Дисперсия - это мера рассеяния значений случайной величины относительно среднего значения:

. (2.7)

Свойства дисперсии:

- дисперсия постоянной величины равна нулю:

s²(с)=0; (2.8)

- постоянную величину можно выносить за знак дисперсии, возведя ее в квадрат:

s²(сх)= с²s²(х); (2.9)

- дисперсия случайной величины равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания:

s²(х)= M(x²)-[M(x)]²; (2.10)

- дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:

s²(х+y)=s²(х)+s²(y); (2.11)

- дисперсия разности двух независимых случайных величин равна разности их дисперсий:

s²(х-y)=s²(х)-s²(y); (2.12)

Среднее квадратическое отклонение – это корень квадратный из дисперсии:

. (2.13)

3. ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

3.1. Элементарные методы первичной

математической обработки

Математическая обработка результатов эксперимента - это неотъемлемая часть любого исследования. Незнание элементарных методов обработки экспериментальных данных нередко приводит к применению упрощенных и недостаточно обоснованных приемов. А это может привести к неточным выводам.

Количественный результат любого опыта в общем случае величина неточная, содержащая некоторую ошибку. Поэтому необходимо оценивать истинное значение измеряемой величины с возможно меньшей ошибкой. Все ошибки, которые содержат отдельные значения измеряемой величины делятся на три типа: промахи (грубые), систематические и случайные . Более подробную информацию об ошибках можно узнать из монографии [1].

Если область применения какой-либо величины разбить на интервалы, то при многократном повторении измерения обнаружим, что отношение количества измерений m_i, попавших в каждый интервал, к общему числу произведенных измерений стремится к некоторому числу, постоянному для каждого интервала. Рассматривая случайные ошибки z=x-a и сами результаты измерения z=x+a как случайные величины, которые могут принимать любые действительные значения, вероятность Р попадания величины z в интервал z_i<z<z_j можно записать в виде:

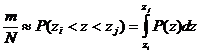. (3.1)

Решение данного уравнения для любого интервала производится в соответствии с знаком или функцией Д(z) распределения вероятностей случайной величины z.

Такая функция нормированная условием

, (3.2)

называется плотностью распределения.

Случайные ошибки измерения наиболее часто характеризуются нормальным законом распределения (закон Гаусса), плотность которого

. (3.3)

График плотности распределения вероятностей называется кривой распределения. Если в формуле (3.3) положить и , то уравнение кривой нормального распределения может быть записано в виде

или , (3.4)

где a - математическое ожидание.

Кривые нормального распределения для различных значений s в формулах (3.3) и (3.4) приведены на рис. 3.1.

Из рис. 3.1. видно, что плотность распределения снижается при увеличении z тем в большей степени, чем меньше s (и больше h). Кроме того, чем меньше s (и больше h), тем меньше разброс ошибок около нуля.

Вероятность (3.1) попадания случайной ошибки в интервал (-z; z) представляет собой заштрихованную площадь криволинейной трапеции под кривой распределения вероятностей (рис. 3.2.).

Рис. 3.1. Вид кривых нормального распределения в зависимости от s

Рис. 3.2. Графическое изображение вероятности попадания случайной ошибки в заданный интервал

При нормальном распределении вероятность непопадания случайной ошибки и пределы s ± 3 является ничтожно малой. Это правило трех сигм, на основании которого при анализе экспериментальных данных производят выявление и устранение грубых ошибок. При этом считают, что наибольшая возможная ошибка не превышает некоторого числа D:

. (3.5)

Все значения, отклоняющиеся от среднего на величину, большую D, исключаются как содержащие грубую ошибку.

В качестве других показателей точности, кроме D, используют также вероятную ошибку (r), среднюю абсолютную ошибку (n), меру точности (Н).

Вероятная ошибка - это величина, которая при большом числе наблюдений делит область распределения ошибок на две равные части, т.е. с одинаковой вероятностью половина отклонений будет меньше r, а половина больше

, (3.6)

где . (3.7)

и характеризует точность отдельных измерений, т.е. показывает насколько тесно ошибки концентрируются около нуля.

Вероятность, что ошибки отдельных измерений не превосходят по абсолютному значению заданной величины ½r½, т.е. заключаются в пределах от -r до +r, может быть описано функцией Ф:

. (3.8)

Значение функции (3.8) при заданной вероятности P определяется по таблицам. Для практических расчетов можно использовать следующие значения, соответствующие трем наиболее часто указываемым уровням:

При P	Значение hr
0,999	2,33
0,99	1,83
0,95	1,39

Средняя абсолютная ошибка отдельного измерения:

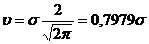. (3.9)

Вычисление среднего значения измеряемой величины к ошибок отдельных измерений не всегда является достаточным при первичной обработке результатов эксперимента. Необходимо также оценить точность полученных результатов: найти меру точности, среднюю квадратическую, вероятную и наибольшую вероятную ошибку среднего арифметического. Мера точности (Н) среднего арифметического определяется из выражения:

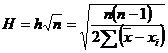, (3.10)

где h - мера точности отдельных измерений.

Средняя квадратичная ошибка (s₀) среднего арифметического определяется из выражения:

. (3.11)

Вероятную ошибку среднего арифметического (r₀) вычисляют по формуле, аналогичной (3.6)

. (3.12)

Наибольшую вероятную ошибку среднего арифметического (D₀) определяют из равенства

. (3.13)

Таким образом, при первичной обработке результатов эксперимента рекомендуется:

- определить и исключить из опытных данных систематическую ошибку;

- вычислить среднее арифметическое ;

- найти среднюю квадратическую s и наибольшую возможную D ошибки отдельного измерения; провести анализ экспериментального материала с целью определения результатов, содержащих грубые ошибки, исключить их и повторить анализ;

- рассчитать среднюю квадратическую ошибку s₀ среднего арифметического; записать его с указанием средней квадратической ошибки;

- в зависимости от характера и цели исследований вычислить остальные характеристики r₀, h и Н. Исходя из условий задачи, может быть принят и другой порядок первичной обработки результатов эксперимента.

Рассмотрим на примере последовательность выполнения основных операций первичной обработки экспериментальных данных.

Пример 3.1. Определить твердость по Роквеллу (НRС) 16 отливок из литой стали марки 45Л. Результаты измерений приведены в табл. 3.1.

1. Анализ данных с целью выявления грубых ошибок показал, что наиболее отличающиеся значения твердости получены в опытах 3 и 9. Их можно было бы исключить как промахи и заменить результатами повторных измерений. Однако для достоверности такого решения проведем анализ с помощью правила трех сигм, т.е. с учетом наибольшей возможной ошибки.

2. Находим среднее арифметическое

Таблица 3.1

Исходные данные для расчета

№	Исходные данные,	Первая обработка		Вторая обработка
№	Исходные данные,
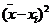
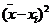
1	32	0	0	32	-1,5	2,25
2	31	1	1	31	-0,5	0,25
3	33	-1	1	33	-2,5	6,25
4	29	3	9	29	1,5	2,25
5	55	-23	529	31	-0,5	0,25
6	32	0	0	32	-1,5	2,25
7	28	4	16	28	2,5	6,25
8	28	4	16	28	2,5	6,25
9	31	1	1	31	-0,5	0,25
10	32	0	0	32	-1,5	2,25
11	33	-1	1	33	-2,5	6,25
12	30	2	4	30	0,5	0,25
13	28	4	16	28	2,5	6,25
14	29	3	9	29	1,5	2,25
15	31	1	1	31	-0,5	0,25
16	30	2	4	30	0,5	0,25
S	512	0	608	488	0	44

3. По формуле (3.5) определяем наибольшую возможную ошибку отдельных измерений D. Для этого в столбец З табл. З.1 заносим отклонения отдельных измерений твердости от среднего арифметического, а в столбец 4 -их квадраты. Равенство суммы говорит о правильности вычислений.

Сравниваем D₁ со значениями 3 столбца. Видно, что в пятом опыте ç23ç> 19,1. Исключаем это значение как грубую ошибку. Опыт №5 повторяем и получаем твердость пятой отливки равную 32 единицам HRC. Заносим это значение в табл. 3.1 и повторяем обработку.

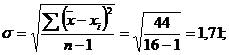
Сравниваем D₂ с результатами опытов (столбец 6). Все результаты удовлетворяют условию.

4. Вычисляем s₀ по формуле (3.11)

Результат обработки можно записать в виде

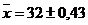
5. По формулам (3.6) и (3.12) определяем вероятные ошибки отдельных измерений и среднего арифметического

5. Меры точности отдельных результатов и среднего арифметического находим по формулам (3.7) и (3.10)

7. Уравнение кривой распределения вероятностей в соответствии с выражением (3.4) имеет вид

3.2. Вторичная обработка результатов эксперимента

Вторичная обработка результатов заключается в представлении их в более наглядном виде: построении графиков, диаграмм, гистограмм, схем, составлении таблиц, построении математических зависимостей типа .

Составление таблиц

Если опытные данные располагать в ряд в порядке их получения в процессе проведения эксперимента, то ряд этот будет малонаглядным. Желательно, поэтому, представить их в определенной последовательности. Этого можно добиться следующим образом:

- опытные данные разбивают на несколько групп;

- все величины в группе представляют одной величиной - центром интервала, который называется признаком группирования;

- для сравнения групп интервала делают одинаковыми по размеру.

Порядок распределения данных по группам следующий:

- определяется интервал группы, в который будут включаться отдельные величины;

- устанавливается расположение интервалов, т.е. границы групп или их центры;

- определяется общая шкала всех интервалов и в них распределяются величины, подученные в процессе наблюдения;

- составляется таблица, которая позволяет наглядно видеть все величины, входящие в группы.

Прерывные и непрерывные величины .делятся на группы по разному.

Пример 3.2. Если случайная переменная величина прерывна и размах варьирования меньше единицы измерения, то интервал группирования принимается равным единице исследуемой случайной переменной величины. В качестве примера приведем исследования производительности (форм/ч) формовочной машины модели 234 М в течение произвольно выбранных 54 рабочих смен. Данные исследования приведены ниже.

12 17 15 12 14 15 14 17 13

14 16 16 13 15 15 15 16 16

13 12 14 16 15 15 15 16 16

16 13 14 16 16 16 16 16 13

14 15 13 14 14 16 15 17 17

Максимальное значение наблюдаемой величины (количество форм в час); х_max = 17, минимальное x_min = 12. Разность между ними (т.е. размах варьирования) х_max - x_min = 17-12 = 5. Эта разность меньше единицы измерения, поэтому интервал группирования можно принять равным единице, а группы составить из отдельных значений изучаемой переменной величины. После этого приступаем к распределения отдельных величин по интервалам (табл. 3.2). В группу 1 заносим признаки группирования, т.е. отдельные значения производительности формовочной машины по мере ее возрастания. В группу 2 - число значений, соответствующих данной производительности, т.е. элементов в каждом интервале группирования. Все значения суммируем и получаем общую сумму наблюдений.

Таблица 3.2

Распределение производительности формовочной машины модели 234М

Признак группирования Частота n_i Относительная частота f_i. Кумулятивная абсолютная частота Кумулятивная относительная частота

12 3 0,067 3 0,067

13 6 0,133 9 0,200

14 8 0,178 17 0,378

15 10 0,222 27 0,600

16 14 0,311 41 0,911

17 4 0,089 45 1,000

S 45 1,000 - -

В результате такой группировки значений изучаемой величины (производительности) получим наглядное распределение производительности формовочной машины.

Для сравнения распределения частоты эмпирических совокупностей необходимо частоты каждой группы разделить на общую совокупность (число наблюдений), т.е. определить относительные частоты

                                   (3.14)

Сумма относительных частот должна быть всегда равна единице. Значения частоты могу" быть выражены в процентах. При этом они покажут, сколько процентов от всей совокупности содержится в каждой группе. Кроме этой частоты можно вычислить также еще кумулятивную частоту (абсолютную и относительную), просуммировав отдельные значения групповой частоты (гр. 4 и 5). Кумулятивная частота показывает, какое количество значений или сколько процентов от всей совокупности равно или меньше границы соответствующего интервала группирования.

Таким образом, из табл. 3.2 можно сделать вывод о том, что в течение 32 смен (71,1%; 8 + 10 +14) производительность машины составляла 14 ... 16 форм/ч. Это значение можно принять основное, т.к. другой производительности соответствует всего 13 смен или 29,9% от всего их количества.

Пример 3.3. Если изучаемая переменная величина является непрерывной, то необходимо выбрать интервал группирования. Желательно, чтобы групп было не слишком мало и в то же время не слишком много. Интервал должен быть выбран таким, чтобы общее число групп было 8...15. При выборе числа групп следует учесть, чтобы величина совокупности охватывалась всеми группами. В качестве примера приведем исследование содержания углерода при анализе плавок стали 35Л для производства отливок. Для исследования выбрали 56 плавок, проведенных в течение 1 года в литейном цехе. Согласно ГОСТ 977-88 "Отливки стальные" содержание углерода должно составлять 0,32-0,40 %. Ниже приведены данные по плавкам.



0,35 0,36 0,30 0,34 0,33 0,35 0,37 0,38

0,35 0,35 0,35 0,35 0,35 0,36 0,37 0,35

0,36 0,30 0,34 0,35 0,38 0,35 0,35 0,46

0,34 0,31 0,33 0,36 0,38 0,41 0,36 0,35

0,32 0,31 0,34 0,37 0,40 0,41 0,37 0,36

0,35 0,32 0,33 0,37 0,39 0,40 0,36 0,35

0,35 0,32 0,35 0,42 0,39 0,38 0,35 0,42

1 2 3 4 5 6 7 8



Определим максимальное и минимальное значения:

х_max = 0,46; x_min = 0,30.

Разделим разность между этими значениями на количество имевшихся групп (например на 8), получим приблизительное значение ширины интервала группирования:

.

После этого приступаем к группированию значений содержания углерода в плавках стали 35Л (табл.3.3). Из опытных данных выбираем те значения, которые входят в ту или иную группу (столбец 1) и записываем их количество в столбец 3. Это есть частота появления того или иного значения в общей сумме.

Возможны затруднения при включении значений, совпадающих с границами групп. Такие величины можно включить в группы следующим образом:

- половину спорных значений включают в низшую группу, а половину - в высшую;

- спорную, величину, совпадающую с границей групп, вписывают в низшую группу; в нашем случае величину 0,32 можно включить в интервал 0,30...0,32;

- спорную величину, совпадающую с границей группы, включают в высшую группу; в нашем случае величину 0,32 можно записать в интервал 0,32...0,34.

Табл. 3.3 составлена по последнему способу. Относительная частота, а также кумулятивная относительная и абсолютная частоты определяются таким же образом, как и для табл.3.2.

Таблица 3.3

Распределение содержания углерода в плавках стали 35Л, %

Граница групп Середина интервала Частота n_i Относительная частота f_i Кумулятивная абсолютная частота Кумулятивная относительная частота

0,30-0,32 0,31 4 0,071 4 0,071

0,32-0,34 0,33 6 0,107 10 0,178

0,34-0,36 0,35 22 0,393 32 0,671

0,36-0,38 0,37 11 0,196 43 0,767

0,38-0,40 0,39 6 0,107 49 0,874

0,40-0,42 0,41 4 0,071 53 0,945

0,42-0,44 0,43 2 0,036 55 0,981

0,44-0,46 0,45 1 0,018 56 1,000

S 56 1,000

Построение графиков

Кроме составления таблиц распределения частоты можно изобразить графически. При построении графиков по оси абсцисс откладывают интервалы группирования, а по оси ординат - абсолютные или относительные частоты. Вид графика зависит от характера изучаемой совокупности.

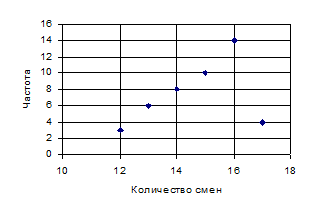
Точечный график. Он применяется для описания распределения прерывной переменной и заключается в нанесении на график в виде точек всех значений переменной. На рис. 3.3 показан график распределения производительности формовочной машины (см. табл. З.2).

Гистограмма. Применяется для изображения распределения частоты непрерывной переменной. Здесь частота распределения изображается прямоугольником, основание которого равно ширине интервала, а высота соответствует частоте. Площади отдельных прямоугольников прямо пропорциональны групповой частоте, а вся площадь, ограниченная диаграммой, прямо пропорциональна общему числу наблюдений. На рис. 3.4 приведена гистограмма распределения содержания углерода в плавках стали 35Л (см. табл. 3.3).

Суммарная гистограмма. Применяется в тех случаях, когда целесообразно графическое изображение кумулятивной частоты. Она аналогична гистограмме с той лишь разницей, что над интервалами группирования строятся прямоугольники, высота которых равна кумулятивной частоте соответствующей группы (рис. З.5).

Рис. 3.3. Точечный график распределения производительности формовочной машины

Рис. 3.4. Гистограмма распределения содержания углерода            в плавках стали 35Л

Рис. 3.5. Суммарная гистограмма распределения содержания            углерода в плавках стали 35Л

    Таким образом, построенные графики позволяют наглядно представить и исследовать распределение частоты исследуемой переменной.

4. ДИСПЕРСИОННЫЙ АНАЛИЗ

Дня сравнения нескольких средних пользуются методом, который основан на сравнении дисперсий и поэтому назван дисперсионный анализом (в основном развит английским статистом Р. Фишером).

На практике дисперсионный анализ применяют, чтобы установить, оказывает ли существенное влияние некоторый качественный фактор А, который имеет К уровней А₁, А₂,…, А_к, на изучаемую величину У. Например, если требуется выяснить, какой элемент наиболее эффективен для получения наибольшей прочности сплава, то фактор А - элемент, а его уровни А₁, А₂,…, А_к - виды элементов, изучаемая величина У - прочность сплава.

Основная идея дисперсионного анализа состоит в сравнении "факторной дисперсии", порождаемой воздействием фактора, и "остаточной дисперсии", обусловленной случайными причинами. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на У; в этом случае средние наблюдаемых значений на каждом уровне (групповые средние) различаются также значимо.

Если уже установлено, что фактор существенно влияет на У, а требуется выяснить, какой из уровней оказывает наибольшее воздействие, то дополнительно производят попарное сравнение средних. В более сложных случаях исследуют воздействие нескольких факторов на нескольких постоянных или случайных уровнях и выясняют влияние отдельных уровней и их комбинаций (многофакторный анализ). Мы ограничимся рассмотрением однофакторного и двухфакторного анализов.

4.1. Анализ однофакторного комплекса

4.1.1. Одинаковое число испытаний на всех уровнях

Пусть на количественный нормально распределенный признак У (например, прочность сплава) воздействует фактор А (элемент), который имеет К постоянных уровней А₁, А₂,…, А_к (виды элементов). На каждом уровне произведено n испытаний. Результаты наблюдений – числа У_ij, где i - номер испытания (i = 1, 2,...,n); j - номер уровня фактора (j = 1, 2,…, К ), - записывают в виде таблицы (табл. 4.1).

                                             Таблица 4.1

Исходные данные для однофакторного дисперсионного анализа с равным числом наблюдений опыта

Номер испытания
Уровни фактора

i А₁ А₂ … А_к

1 У₁₁ У₁₂ … У_1к

2 У₂₁ У₂₂ … У_2к

… … … … …

n У_n1 У_n2 ... У_nк

N …

Алгоритм проведения дисперсионного анализа

1. Итоги по столбцам

.                                 (4.1)

2. Сумма квадратов всех наблюдений

.                             (4.2)

3. Сумма квадратов итогов по столбцам, деленная на число наблюдений в столбце

.                              (4.3)

4. Квадрат общего итога, деленный на число всех наблюдений (N)

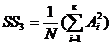.                           (4.4)

5. Сумма квадратов для столбца

.                            (4.5)

6. Общая сумма квадратов, равная разнице между суммой квадратов всех наблюдений и корректирующим членом (SS₃)

.                           (4.6)

7. Остаточная сумма квадратов

.                           (4.7)

8. Дисперсия фактора А

.                                  (4.8)

9. Общая дисперсия

.                                (4.9)

Для оценки влияния фактора используют критерий Фишера. Дня этого сравнивают расчетный критерий Фишера

.                              (4.10)

с табличным.

Табличный критерий Фишера находится по прил. табл. 1, 2 для следующих степеней свободы:

f₁=к-1;

f₂=к(n-1);

к – уровни;

n – количество опытов.

Влияние фактора А считается значимым, если расчетный критерий Фишера больше табличного:

F_{А расч} > F_{А табл},                          (4.11)

и не значимо, если наоборот.

Дисперсия 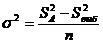служит количественной оценкой влияния фактора А на отклик.

Замечание 1. Если факторная дисперсия ( 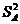) окажется меньше остаточной, то уже отсюда непосредственно следует справедливость нулевой гипотезы о равенстве групповых средних, поэтому дальнейшие вычисления (сравнение дисперсий с помощью критерия Фишера) излишни.

Замечание 2. Если наблюдаемые значения У_ij десятичный дроби с k знаками после запятой, то целесообразно перейти к целым числам

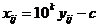,                            (4.12)

где с - примерно среднее значение чисел .

При этом факторная и остаточная дисперсий увеличится каждая в 10^2k раз, однако их отношение не изменится.

Пример 4.1. Каждый из 3 видов сплавов чугуна С415 с Ni (А₁), Тi (А₂), Cr (A₃) был изготовлен по 4 плавки (т.е. с одинаковым числом испытаний. У всех двенадцати сплавов определена прочность на разрыв (изучаемая величина У ). Результаты испытаний приведены в табл. 4.2.

Решение. Для упрощения расчета вычтем из каждого наблюдаемого значения У_ij общую среднюю = 29, т.е. перейдем к уменьшенным величинам Х_ij = У_ij - 29. Например, Х₁₁- 29 = 9. Составим расчетную табл. 4.3.

Таблица 4.2.

Результаты испытаний

Номер испытания

i

Уровни фактора

А₁ А₂ А₃

1 38 20 21

2 36 24 22

3 35 26 31

4 31 30 34

35 25 27

Таблица 4.3

Расчетная таблица

Номер испытания i

Уровни фактора

Итоговый столбец

F₁

F₂

F₃

Х_i1 Х²_i1 Х_i2 Х²_i2 Х_i3 Х²_i3

1 9 81 -9 81 -8 64

2 7 49 -5 25 -7 49

3 6 36 -3 9 2 4

4 2 4 1 1 5 25

170 116 142

24 -16 -8

576 256 64

где – сумма квадратов уменьшенных значений признака на уровне A_j.

Используя итоговый столбец табл. 4.3, найдем общую и факторную суммы квадратов отклонений, учитывая, что число уровней фактора К = 3, число испытаний на каждом уровне n=4;

;

.

Найдем остаточную сумму квадратов отклонений:

.

Найдем остаточную дисперсию, для этого разделим S_ост на число степеней свободы к(n-1) = 3 (4 - 1) = 9.

.

Найдем факторную дисперсию, для этого разделим S_факт на число степеней свободы к-1 = 3 - 1 = 2.

.

Сравним факторную и остаточную дисперсии с помощью критерия Фишера - Спедекора. Для этого сначала найдем наблюдаемое значение критерия

.

Учитывая, что число степеней свободы числителя f₁ = 2, а знаменателя f₂ = 9 и что уровень значимости a = 0,05 (прил. табл. 1) находим критическую точку

F_крит(0,05;2;9) = 4,3.

Т.к. F_набл > F_крит - нулевую гипотезу о равенстве групповых средних отвергаем. Другими словами, групповые средние в целом различаются значимо.

4.1.2. Разное количество испытаний на различных уровнях

Если число испытаний на уровне А₁ равно n₁, на уровне А₂ – n₂,…, на уровне А_к - n_к, то общую сумму квадратов отклонений вычисляют как и в случае одинакового числа испытаний на всех уровнях. Факторную сумму квадратов отклонений находят по формуле

,     (4.13)

где N = n₁+n₂+…n₃ - общее число испытаний;

- сумма уменьшенных значений признака на уровне А_j.

Остальные вычисления производят, как в случае одинакового числа испытаний.

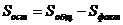;                       (4.14)

; . (4.15)

.

Пример 4.2. Получено 4 вида сплавов группы СЧ15: 1-й с Ni(первый уровень А₁); 2-й c Ti (второй уровень А₂); 3-й с Cr (третий уровень А₃); 4-й с Mo (четвертый уровень А₄). При этом 1-й и 2-й сплавы изготавливались по 4 плавки; 3-й сплав - 3 плавки и 4-й сплав - 2 плавки. У всех 13 полученных плавок определялось относительное удлинение в % (изучаемая величина У). Результаты испытаний приведены в табл. 4.4.

Таблица 4.4

Результаты испытаний

Номер

испытания i

Уровни фактора

A₁ A₂ A₃ A₄

1 1,38 1,41 1,32 1,31

2 1,38 1,42 1,33 1,33

3 1,42 1,44 1,34 -

4 1,42 1,45 - -

Групповая средняя 1,40 1,43 1,33 1,32

Решение. Используя замечание 2 (разд. 4.1.1), перейдем к целым числам .

Составим расчетную табл. 4.5.

Используя итоговый столбец и нижнюю) строку табл. 4.5, найдем общую и факторную суммы квадратов отклонений

;

Таблица 4.5

Расчетная таблица

Номер испытания i

Уровни фактора

Итоговый столбец

А₁

А₂

А₃

А₄

Х_i1 Х²_i1 Х_i2 Х²_i2 Х_i3 Х²_i3 Х_i4 Х²_i4

1 0 0 3 9 -6 36 -7 49

2 0 0 4 16 -5 25 -5 25

3 4 16 6 36 -4 16 - -

4 4 16 7 49 - - - -

32 110 77 74

8 20 -15 -12

64 400 225 144

где – сумма квадратов уменьшенных значений признака на уровне A_j.

=

=64/4+400/4+225/3+144/2-0,08=262,92.

Найдем остаточную сумму квадратов отклонений.

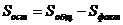= 292,92 – 262,92 = 30.

Найдем факторную и остаточную дисперсии

= 262,92/(4-1)=262,92/3=87,64;

=30/(13-4)=30/9=3,33.

Сравним факторную и остаточную дисперсии с помощью критерия Фишера. Для этого сначала вычислим наблюдаемое значение критерия. Учитывая, что число степеней свободы числителя f₁= к –1 = 4 – 1 = 3, знаменателя f₂= N – к = 13 – 4 = 9 и что уровень значимости a = 0,05, по прил. табл. 1 находим критическую точку F_кр (0,05; 3; 9) = 3,9.

Т.к. F_набл > F_табл – нулевую гипотезу о равенстве групповых средних отвергаем. Другими словами, групповые средние различаются значимо.

4.2. Анализ двухфакторного комплекса

Данный вид дисперсионного анализа предусматривает оценку влияния 2-х факторов А и В на нескольких уровнях на отклик У, а также оценку влияния взаимодействия факторов А, В на тот же У.

Факторы А и В могут варьироваться на нескольких, но не обязательно равных между собой уровнях (табл. 4.6).

Таблица 4.6

а₁ а₂ а₃ а₄ а₅

в₁ у₁₁ у₁₂ у₁₃ у₁₄ у₁₅

в₂ 21 у₂₂ у₂₃ у₂₄ у₂₅

в₃ 31 у₃₂ у₃₃ у₃₄ у₃₅

,           (4.16)

где a_ij - эффект влияния фактора А на i-м уровне (i изменяется от 1 до µ);

b_ij - эффект влияния фактора В на i-м уровне (i изменяется от 1 до µ);

a_ib_i - эффект взаимодействия факторов, который показывает зависимость силы влияния одного из факторов от      уровня на котором находится другой фактор;

m+a_ij+b_ij - отклонение от суммы первых трех членов;

e_ijq - показывает вариацию внутри значения (клетки).

Алгоритм расчета при линейной модели

дисперсионного анализа

Таблица 4.7

Данные для двухфакторного дисперсионного

анализа, без повторений опыта

В

А

Итого

а₁ а₂ … а_к

в₁ у₁₁ у₁₂ … у_к1 В₁

в₂ у₂₁ у₂₂ … у_к2 В₂

… … … … … …

в_m у_m1 у_m2 … у_mк В_m

Итого А₁ А₂ … А_к

Модель               .               (4.17)

Находим:

1. Итоги по столбцам

, i = 1,2,…, к.                      (4.18)

2. Итоги по строкам

, i = 1,2,…, m.                      (4.19)

3. Сумму квадратов всех наблюдений

.                             (4.20)

4. Сумму квадратов итогов по столбцам, деленную на число наблюдений в столбце

.                              (4.21)

5. Сумму квадратов итогов по строкам, деленную на число наблюдений в строке

.                              (4.22)

6. Квадрат общего итога, деленный на число всех наблюдений

.              (4.23)

7. Сумму квадратов для столбца

.                         (4.24)

8. Сумму квадратов для строки

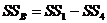.                         (4.25)

9. Общую сумму квадратов, равную разнице между разницы суммы квадратов всех наблюдений и корректирующим членом (SS₄)

.                       (4.26)

10. Остаточную сумму квадратов

. (4.27)

11. Дисперсию фактора А

.                                  (4.28)

12. Дисперсию фактора В

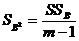.                                  (4.29)

13. Выборочную дисперсию

.                          (4.30)

Расчеты критерия Фишера по А и В

, F_табл_А при f₁ = к-1;              (4.31)

f₂ =(к-1)(m-1)

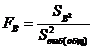, F_{табл B} при f₁ = m-1;              (4.32)

f₂ =(к-1)(m-1)

Дальнейший ход рассуждений аналогичен однофакторному дисперсионному анализу. Результаты расчетов сводятся в табл. 4.8.

Таблица 4.8

Двухфакторный дисперсионный анализ

линейных моделей

Источник дисперсии Число степеней свободы Сумма квадратов Средний квадрат

А к – 1

В m – 1

Остаток (к – 1)(m – 1)

Общая сумма кm - 1

Определив с помощью анализа значимость каждого из факторов, вычисляют какие именно средние значения различны, между собой, используя критерий Стьюдента или Дункана.

Нелинейная модель двухфакторного дисперсионного анализа

   Алгоритм расчета для нелинейной модели.

При расчете опираемся на данные табл. 4.7.

1. Сумма наблюдений в каждой ячейке

,      j=1,2,…,m; i=1,2,…,n. (4.33)

2. Квадрат сумм наблюдений в каждой ячейке

.                              (4.34)

3. Итоги по столбцам

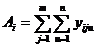.                              (4.35)

4. Итоги по строкам

.                               (4.36)

5. Сумма всех наблюдений

.                (4.37)

6. Сумма квадратов всех наблюдений

.                           (4.38)

7. Сумма квадратов итогов по столбцам, деленная на количество наблюдений в столбце

.                               (4.39)

8. Сумма квадратов итогов по строкам, деленная на количество наблюдений в строке

.                               (4.40)

9. Квадрат общего итога, деленный на число всех наблюдений

. (4.41)

10. Сумма квадратов для столбца

.                          (4.42)

11. Сумма квадратов для строки

.                          (4.43)

12. Сумма квадратов для дисперсии воспроизводимости

       .                      (4.44)

13. Общую сумму квадратов, равную разнице между суммой квадратов всех наблюдений и корректирующим членом

     .                         (4.45)

14. Остаточную сумму квадратовотклонений для эффекта взаимодействия АВ

.          (4.46)

15. Дисперсию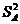

.                              (4.47)

16. Дисперсию

.                              (4.48)

17. Дисперсию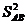

.                       (4.49)

18. Дисперсию воспроизводимости

.                              (4.50)

19. Сведем результаты расчета в табл.4.9 двухфакторного дисперсионного анализа

Таблица 4.9

Двухфакторный дисперсионный анализ,

нелинейная модель

Источник дисперсии Число степеней свободы Сумма квадратов Средний квадрат

А к – 1

В m – 1

АВ (к – 1)(m – 1)

Остаток mк(n – 1)

Общая сумма кmn - 1 -

20. Значимость линейных эффектов А и В и АВ проверим по критерию Фишера

>< F_табл_А при f₁ = к-1;              (4.51)

f₂ =(к-1)(m-1)

>< F_{табл B} при f₁ = m-1;              (4.52)

f₂ =(к-1)(m-1)

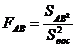>< F_{табл B} при f₁ = (к-1)(m-1);      (4.53)

f₂ =кm(к-1)

Оценка значимости фиксированными уровнями

>< F_табл_А при f₁ = к-1;               (4.54)

f₂ = кm(n-1)

>< F_{табл B} при f₁ = m-1;              (4.55)

f₂ = кm(n-1)

Пример 4.3. Методом двухфакторного дисперсионного анализа оценить значимость влияния на твердость стали 25х2НЧДМАФЛ температур закалки и отпуска. План и результаты эксперимента представлены в табл. 4.10. При каждом сочетании температур закалки и отпуска проделано 2 параллельных опыта.

                                            Таблица 4.10

Результаты экспериментов

В (температура отпуска, ^оС)

А (температура закалки, ^оС)

а₁ а₂ а₃

880 930 980

в₁ 570 401 403 415 417 428 430

в₂ 620 361 363 362 364 363 365

в₃ 670 321 323 339 341 353 351

Решение. Математическая модель эксперимента представляет собой модель с фиксированными уровнями. Уровни факторов А и В выбраны неслучайно, поскольку необходимо установить влияние на твердость только данных трех температур закалки и отпуска. Расчет проводится согласно алгоритма по формулам 4.33 – 4.55.

1. Определим суммы наблюдений в каждой ячейке (табл. 4.11).

Таблица 4.11

В

А

Итоги

а₁ а₂ а₃

в₁ 804 832 858 2494

в₂ 724 726 728 2178

в₃ 644 680 704 2028

Итоги 2172 2238 2290 6700

2. Возведем полученные суммы в квадрат. Результаты представим в виде табл. 4.12.

Таблица 4.12

В

А

а₁ а₂ а₃

в₁ 646416 692224 736164

в₂ 524176 527076 529984

в₃ 414736 462400 495616

3. Итоги по столбцам

А₁=2172; А₂=2238; А₃=2290.

4. Итоги по строкам

В₁=2494; В₂=2178; В₃=2028.

5. Общий итог – сумма всех наблюдений

= 6700.

6. Сумма квадратов всех наблюдений

= 6700²= 44890000

7. Определим сумму квадратов итогов по столбцам, деленную на количество наблюдений в столбце

=1/(3×2) (2172²+2238²+2290²)=2495054.

8. Сумма квадратов итогов по строкам, деленная на количество наблюдений в строке

=1/(3×2) (2172²+2238²+2290²)=2512750.

9. Квадрат общего итога, деленный на число всех наблюдений

6700²/18=2493888.

10. Сумма квадратов для столбца

=7765,8.

11. Сумма квадратов для строки

=78361,8.

12. Сумма квадратов для дисперсии воспроизводимости

= 44890000-(646416+…+495616)/2=18.

13. Общую сумму квадратов, равную разнице между суммой квадратов всех наблюдений и корректирующим членом

=20525,2.

14. Остаточную сумму квадратовотклонений для эффекта взаимодействия АВ

=479,6.

15. Определим соответствующие дисперсии

=582,9;

=9430,9;

=117,9;

=2.

16. Сведем результаты расчета в табл.4.13 двухфакторного дисперсионного анализа

Таблица 4.13

Двухфакторный дисперсионный анализ,

нелинейная модель

Источник дисперсии Число степеней свободы Сумма квадратов Средний квадрат

А 2 7765,8 582,9

В 2 78861,8 9430,9

АВ 4 479,6 119,9

Остаток 9 18 2

Общая сумма 17 20524,4 -

17. Значимость линейных эффектов А и В и АВ проверим по критерию Фишера

Оценка значимости фиксированными уровнями

=291,45;

=4715,45;

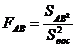=59,95.

Табличное значение F_табл для r = 0,05 и числа степеней свободы f₁=2, f₂=9 для А и В, F_табл = 4,3.

Поскольку рассчитанное дисперсионное отклонение больше табличного, фактор А и В значимы, т.е. твердость зависит и от температуры закалки и от температуры отпуска.

F_табл для АВ, при r = 0,05 и числе степеней свободы f₁=4, f₂=9, составит 3,6.

Поскольку F_АВ > F_табл для АВ; эффект взаимодействия также следует признать значимым. Таким образом, интенсивность влияния температур закалки на твердость зависит от температуры отпуска, и наоборот - сила влияния температура отпуска на твердость зависит от температуры закалки.

5. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

В природе, технике различные явления, параметры, величины могут быть несвязанными друг с другом, могут быть относительно связанными или иметь строгую зависимость в виде той или иной функции. В статистике разработаны методы для оценки относительно связанных друг с другом случайных величин. Такая зависимость может проявляться в том, что при изменении одной случайной величины изменяется закон распределения другой (зависимой) случайной величины или в том, что при изменении первой случайной величины изменяется среднее значение второй случайной величины. В последнем случае говорят, что между случайными величинами существует статистическая зависимость или корреляция. На рис. 5.1 представлено поле рассеяния двух статистически зависимых величин Х и У.

При корреляционном анализе оценивают тесноту связи переменных и определяют вид этой связи (прямая пропорциональная, квадратичная, логарифмическая и т.д.)

5.1. Коэффициент корреляции

Теснота связи между случайными величинами Х и У оценивается коэффициентом корреляции. Для зависимости, изображенной на рис. 5.1 рассчитывают выборочный линейный коэффициент корреляции. Его также называют парным коэффициен-

Рис 5.1. Поле рассеяния двух статистически зависимых величин Х и У

том корреляции (5.1).

.             (5.1)

Он может изменяться от -1 до +1. Чем больше по абсолютной величине коэффициент корреляции, тем меньше рассеяние экспериментальных точек. Когда =1, зависимость не статистическая, а строчная линейная. Когда = 0, или близко к 0, то линейной зависимости нет. Однако в этом случае может быть нелинейная зависимость (рис.5.2), поэтому в этом случае дополнительно следует делать проверку корреляционного отношения h_у/х.

Если зависимость статистическая линейная, т.е. >0 то знак коэффициента корреляции указывает на характер изменения случайной величины У в зависимости от изменения Х. Так если положительное, то значения У возрастают при возрастании X. Выражение (5.1) можно преобразовать к виду, более удобному для расчетов при небольшом количестве наблюдений

Рис. 5.2. Статистическая нелинейная зависимость между случайными величинами Х и У

.                             (5.2)

Пример 5.1. Рассчитать коэффициент корреляции между содержанием титана Х и проделом прочности при растяжении У по выборке из 13 плавок стали одной марки.

Полученные в исследовании значения Ti и s_в занесены в 1 и 2 колонки табл.5.1. В остальных колонках приведены дополнительные данные, необходимые для расчета по выражению (5.2).

Для расчета требуется определить средние арифметические значения Х и У

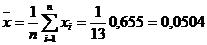% Ti

Таблица 5.1

Расчет коэффициента корреляции между содержанием титана и пределом прочности стали при малом количестве наблюдений

№ Содержание титана, % Хi Предел прочности, Мпа (x_i-x) (x_i-x)² (y_i-y) (y_i-y)² х*у

1 0,025 290 -0,0254 0,0006 -30,385 923,225 7,25

2 0,03 295 -0,0204 0,0004 -25,385 644,379 8,85

3 0,032 290 -0,0184 0,0003 -30,385 923,225 9,28

4 0,04 310 -0,0104 0,0001 -10,385 107,840 12,4

5 0,046 320 -0,0044 0,0000 -0,385 0,148 14,72

6 0,048 315 -0,0024 0,0000 -5,385 28,994 15,12

7 0,05 323 -0,0004 0,0000 2,615 6,840 16,15

8 0,054 330 0,0036 0,0000 9,615 92,456 17,82

9 0,056 324 0,0056 0,0000 3,615 13,071 18,144

10 0,06 345 0,0096 0,0001 24,615 605,917 20,7

11 0,07 330 0,0196 0,0004 9,615 92,456 23,1

12 0,072 338 0,0216 0,0005 17,615 310,302 24,336

13 0,072 355 0,0216 0,0005 34,615 1198,225 25,56

S 0,655 4165 0 0,0030 0 4947,077 213,43

МПа

и среднеквадратические отклонения S_x и S_у

%

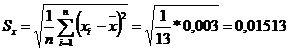МПа

Подставляя данные из табл. 5.1, рассчитаем коэффициент парной корреляции

Получим довольно высокое значение коэффициента парной корреляции, однако окончательно вывод о том, существует ли статистическая зависимость между Х и У делают на основании сравнения расчетного коэффициента корреляции с критическим , который определяют по прил. табл. 3. Если > , то для данного числа наблюдений k коэффициент корреляции является значимым, т.е. с вероятностью Р можно утверждать, что существует зависимость У от X. В примере = 0,8041, k=13. Для вероятности Р = 0,95 находим = 0,5139 (см. прил. табл. 3), для вероятности Р = 0,99 - = 0,6411. Следовательно, с вероятностью 0,95 и 0,99 можно утверждать, что существует положительная связь содержания Ti в стали с ее прочностью, т.к. > и > .

Для большого числа опытов (n>100) значимость можно оценивать по t – отношению, которое часто называют критерием Стьюдента, статистическая линейная зависимость существует при условии, что критерий Стьюдента

>2,6,

где - среднее квадратическое отклонение коэффициента корреляции.

5.2. Коэффициент множественной корреляции

Часто случайная величина У зависит от нескольких случайных величин Х₁, Х₂, Х₃ и т.д. В этом случае наличие зависимости У от Х проверяется с помощью коэффициента множественной корреляции R. Если количество независимых переменных равно двум, R может быть рассчитано следующим образом:

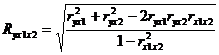,              (5.3)

где - величины парных коэффициентов корреляции   для всех возможных комбинаций переменных У, Х₁, Х₂.

Коэффициент множественной корреляции принимает только положительные значения, поэтому нельзя установить знак зависимости с его помощью. Теснота связи определяется так же, как по коэффициенту парной корреляции: чем ближе значение 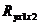к 1, тем меньше рассеяние экспериментальных точек. Графически это изображается полем рассеяния относительно некоторой плоскости в 3-мерном пространстве (рис. 5.3).

Рис.5.3. Поле рассеяния случайной величины У

При зависимости У от нескольких X_i можно выделить влияние какой-либо одной случайной величины. Такая оценка называется частным или парциальным коэффициентом корреляции. Расчет предполагает закрепление всех остальных переменных на постоянном уровне. Для двух независимых переменных расчет ведется по формулам:

- для исключения влияния X₂

;                  (5.4)

- для исключения влияния Х₁

.                  (5.5)

Пример 5.2. При исследовании механических характеристик стали получена выборка из 33 наблюдений для предела текучести s_т, предела прочности s_в и предела выносливости при симметричном изгибе s_-1. По выражению (5.5) рассчитано, что 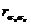= -0,825; = -0,69; = 0,57. Определить коэффициент множественной корреляции между этими величинами и парциальный коэффициент корреляции.

По формуле (5.3) коэффициент множественной корреляции равен

.

Получили высокое значение коэффициента корреляции. Так же, как и в случае парного коэффициента корреляции требуется статистическая оценка значимости. Для коэффициента множественной корреляции оценка значимости производится при помощи дисперсионного анализа, который заключается в определении характеристики F и сравнении ее с табличным значением критерия Фишера для числа независимых переменных К₁, числа степеней свободы к₂=n-К₁ и для выбранной ошибки a (в технике чаще всего принимают ошибку a = 0,05). Если F>F_0.05 (к₁; к₂), то считают что существует зависимость между Х_i и У. Характеристика F рассчитывается следующим образом:

,                  (5.6)

где n - объем выборки;

к₁ - число независимых переменных.

Для множественной корреляции с тремя случайными переменными, т.е. с двумя независимыми переменными F равно

.                          (5.7)

В примере 5.2 выборка состоит из n = 33 наблюдений, поэтому

.

Т.к. табличный критерий Фишера F_0.05 (2, 30) =3,316 и 31,52 > 3,316, то можно сделать вывод о том, что существует статистическая зависимость между s_т, s_в и s_-1, и коэффициент множественной корреляции   значим.

Оценка парциального коэффициента корреляции

.

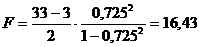Т.к. 16,43 > 3,316, получился значимым, поэтому при исключении влияния s_-1, связь между значениями s_т, и s_висследованной стали существует. Опыт многочисленных исследований подтверждает этот вывод. Всегда при повышении предела прочности наблюдается некоторое повышение предела текучести стали.

6. РЕГРЕССИОННЫЙ АНАЛИЗ

Когда необходимо количественно охарактеризовать зависимость между двумя или более параметрами, возможностей корреляционного анализа становится недостаточно. В этом случае используют линейные парные, линейные множественные и нелинейные уравнения регрессии. Регрессионный анализ [3, 4, 8] заключается в поиске коэффициентов уравнений регрессии и в статистической оценке результатов расчета по полученным уравнениям.

Необходимо отметить, что по одним и тем же результатам эксперимента можно получить несколько уравнений регрессии, т.к. перед началом обработки этих результатов предварительно задаются видом функции. Полученные уравнения могут с большей или меньшей точностью описывать реальный объект, поэтому выбирают наиболее точное, а также такое, которое не противоречит представлениям об объекте или происходящих в нем процессах. Уравнение регрессии, включающее несколько независимых факторов, может оказаться громоздким, неудобным для применения. Если не пострадает точность, следует учитывать в уравнении только наиболее сильные факторы и отказываться от второстепенных.

При нескольких независимых факторах расчет коэффициентов уравнений регрессии и проверка их адекватности представляет значительные сложности, поэтому студенту в научной работе необходимо уметь использовать ЭВМ.

6.1. Парный линейный регрессионный анализ

Простейшее уравнение регрессии – это уравнение прямой на плоскости в декартовых координатах

y = b₀+ b₁x,                                 (6.1)

где b₀и b₁ - коэффициенты уравнения регрессии;

х - независимая переменная (фактор);

у - функция отклика.

Коэффициент b₀(свободный член уравнения регрессии) геометрически представляет собой расстояние от начала координат до точки пересечения линии регрессии с ординатой (рис. 6.1). Коэффициент b₁ - тангенс угла наклона линии регрессии к оси абсцисс. Задача линейного регрессионного анализа (метода наименьших квадратов) состоит в том, что, зная положения экспериментальных точек так провести линию регрессии, чтобы сума квадратов отклонений этих точек от полученной прямой была минимальной.

Рис. 6.1. Графическая интерпретация коэффициентов уравнения регрессии.

Если неизвестны средние значения 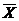и , коэффициенты b₀ и b₁определяют следующим образом:

;                  (6.2)

.                       (6.3)

Пример 6.1. Построить линию регрессии для исходных данных, приведенных в табл. 6.1.

                                             Таблица 6.1

Исходные данные

1 2 3 4 5 6 7 8

Х 1,5 4,0 5,0 7,0 8,5 10,0 11,0 12,5

У 5,0 4,5 7,0 6,5 9,5 9,0 11,0 9,0

Вычисление коэффициентов линейного уравнения регрессии проводится с помощью данных, поведенных в табл. 6.2.

Таблица 6.2

Таблица вспомогательных данных, необходимых для расчета коэффициентов регрессии

№ х² у² ху х+у (х+у)²

1 2,25 25,00 7,50 6,50 42,25

2 16,00 20,25 18,00 8,50 72,25

3 25,00 49,00 35,00 12,00 144,00

4 49,00 42,25 45,50 13,50 182,25

5 72,25 90,25 80,75 18,00 324,00

6 100,00 81,00 90,00 19,00 361,00

7 121,00 121,00 121,00 22,00 484,00

8 156,25 81,00 112,50 21,50 462,25

S 541,75 509,75 510,25 121,00 2072,00

Тогда

;

.

Окончательно уравнение регрессии имеет вид

у = 3,73 + 0,53х

а геометрическое представление приведено на рис. 6.1.

Если рассчитаны средние значения Х и У, то можно использовать следующие формулы:

;                     (6.4)

.                               (6.5)

Если рассчитан коэффициент корреляции и средние квадратические отклонения S_x и S_y, то для расчета коэффициента регрессии b₁ можно использовать формулу

,                                (6.6)

а свободный член уравнения регрессии может быть определен по формуле (6.5).

Пример 6.2. Получить зависимость твердости синтетического серого чугуна от размеров графитовых включений для условий ФЛЦ ММК. Исходные данные и необходимые промежуточные значения приведены в табл.6.3.

Таблица 6.3

Данные для расчета уравнения регрессии, связывающего твердость и размеры графитовых включений синтетического                     серого чугуна

№ Средние размеры графитовых включений хi, мкм Твердость серого чугуна по Бриннелю уi, МПа (x_i-x) (x_i-x)² (y_i-y) (y_i-y)² х*у

1 104 187 -11,667 136,111 1,75 3,063 19448

2 99 184 -16,667 277,778 -1,25 1,563 18216

3 108 192 -7,667 58,778 6,75 45,563 20736

4 100 187 -15,667 245,444 1,75 3,063 18700

5 110 179 -5,667 32,111 -6,25 39,063 19690

6 120 180 4,333 18,778 -5,25 27,563 21600

7 144 170 28,333 802,778 -15,25 232,563 24480

8 198 161 82,333 6778,778 -24,25 588,063 31878

9 153 180 37,333 1393,778 -5,25 27,563 27540

10 90 200 -25,667 658,778 14,75 217,563 18000

11 83 201 -32,667 1067,111 15,75 248,063 16683

12 79 202 -36,667 1344,444 16,75 280,563 15958

S 1388 2223 0 12814,667 0 1714,250 252929

Расчет коэффициентов регрессии

Определим среднеарифметическое значение фактора

мкм.

и среднее квадратическое отклонение фактора

мкм.

Среднеарифметическое значение параметра

МПа

и среднее квадратическое отклонение параметра

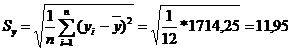Мпа.

Определим коэффициент корреляции

и коэффициенты регрессии

;

.

По полученным коэффициентам запишем уравнение регрессии

у = 220,1 - 0,3х                                (6.7)

или

НВ = 220,1 –0,3 Г_раз.

Для построения линии регрессии задаемся двумя любыми значениями фактора, например, Х₁ = 80 мкм и Х₂ = 180 мкм. Расчетные значения параметра при выбранных значениях Х равны: У₁ = 220,1 - 0,3*60 = 196,1 МПа и У₂ = 220,1 - 0,3*180 = 166,1 МПа. По данным расчета строим линию регрессии, которая представлена на рис. 6.2.

В порядке рекомендации по построению графиков отметим, что расчетные кривые представляются без нанесения точек, по которым они были построены. Т.е. в нашем случае нет точек Х₁ = 80 мкм, У₁ = 196,1 МПа и Х₂ = 180 мкм, У₂ =166,1 МПа, а нанесены только данные по 12 пробам чугуна. Знак коэффициента корреляции и коэффициента b₁ в уравнении регрессии показывают, что график зависимости НВ = f(Граз)должен быть ниспадающей прямой. И действительно, при укрупнении графитовых включений в сером чугуне твердость снижается. Полученное уравнение не противоречит физическим представлениям о механических свойствах серого чугуна.

Рис. 6.2. Зависимость твердости синтетического чугуна от параметров включений графита

     Проверка адекватности уравнения регрессии

Для проверки адекватности уравнения регрессии сравнивают общую дисперсию с остаточной дисперсией представляет собой показатель ошибки предсказания результатов расчета о помощью уравнения регрессии

.                        (6.8)

Для того, чтобы уравнение регрессии было значимо, необходимо, чтобы выполнялось условие

,                          (6.9)

где F_a_(к1,к2) - критерий Фишера для выбранной ошибки.

Числа степеней свободы определяются

к₁= n - 1; к₂= n - l,

где l - число коэффициентов уравнения регрессии.

Критерий Фишера выбирается по прил. табл. 2. Для примера к₁= 11; к₂= 10. Если выбрать обычный для технических расчетов a = 0,05, то F_0,05(11,10) = 2,94. Вычисление можно провести в табличной форме.

Расчет остаточной дисперсии

Таблица 6.4

Расчет остаточной дисперсии для примера

№ х_i у_i

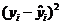
1 104 187 220,1 - 0,3 × 104 = 188,9 -1,9 3,81

2 99 184 220,1 - 0,3 × 99 = 190,3 -6,3 39,6

3 106 192 220,1 - 0,3 × 108 = 187,7 +4,3 17,4

4 100 187 220,1 - 0,3 × 100 = 190,1 -3,1 9,6

5 110 179 220,1 - 0,3 × 110 = 187,1 -8,1 64,9

6 120 180 220,1 - 0,3 × 120 = 184,1 -4,1 16,8

7 144 170 220,1 - 0,3 × 144 = 176,9 -6,9 47,6

8 198 161 220,1 - 0,3 × 198 = 158,4 +2,6 6,3

9 153 180 220,1 - 0,3 × 153 = 174,2 +5,8 33,6

10 90 200 220,1 - 0,3 × 90 = 193,1 +6,9 47,6

11 83 201 220,1 - 0,3 × 83 = 195,2 +5,8 33,6

12 79 202 220,1 - 0,3 × 79 = 196,4 +5,6 31,3

353,2

Расчетное значение

.

Получим, что F > F_0,05(11,10) поэтому считается, что уравнение У = 220,1 - 0,ЗХ адекватно описывает результаты экспериментов.

6.2. Множественный линейный регрессионный анализ

На практике наиболее простой парный линейный регрессионный анализ встречается реже, чем множественный. Однако, ввиду сложности обработки результатов исследований при действии на функцию отклика У_i нескольких факторов Х_i, задачу упрощают и искусственно приводят ее к парной регрессии. Вообще при множественном линейном регрессионном анализе задача формулируется как отыскание коэффициентов b₀ иb_j в полиноме вида

У=b₀+b₁x₁+b₂x₂+b₃x₃+…+b_jx_j+…b_px_p.            (6.10)

Результаты наблюдений при множественном линейном регрессионном анализе записываются в виде матрицы

     (6.11)

где р - число факторов; n - количество опытов; х_ij - значение j -го фактора для i - го опыта; у_i - значение функции отклика для i - го опыта; у_n - значение функции отклика в последнем опыте.

Коэффициенты уравнения регрессии определяются методом наименьших квадратов, исходя из условия:

,                    (6.12)

где - расчетное значение функции отклика в i -ом опыте.

Т.к. , то условие (6.12) называемое невязкой, можно записать

.     (6.13)

Невязка минимальна, если выполняются условия

; ; ; … ; . (6.14)

Эти уравнения образуют систему нормальных уравнений:

;

… … … … … … … … … … … … … …… … … … … … …… … … …

(6.15)

… … … … … … … … … … … … … …… … … … … … …… … … …

.

При большом объеме выборки задача статистического описания должна быть представлена в матричной форме и обрабатываться на ЭВМ. В случае зависимости у= f(х₁, х₂) процедура вычисления значительно упрощается. Однако в атом случае предварительно требуется определить S_у, S_х1, S_х2, , , и коэффициенты корреляции для всех возможных комбинаций между переменными у, х₁ и х₂: , , . Уравнение ищется в виде

,            (6.16)

где коэффициенты b₁ и b₂ определяются по формулам

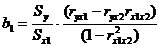;                (6.17)

.               (6.18)

Для приведения уравнения (6.10) к виду y=b₀+b₁x₁+b₂x₂ требуется подставить коэффициенты b₁ и b₂ в уравнение (6.16) и произвести вычисления.

Пример 6.3. При обработке результатов исследования влияния содержания серы (х₁) и фосфора (х₂) на ударную вязкость стали (у) было получено

= -0,592; = 12,755; S_у = 1,0912;

= -0,268; = 0,0159; S_х1 = 0,00354;

= 0,260; = 0,0119; S_х2 = 0,00324.

Расчет коэффициента b₁ ведем по формуле (6.17)

коэффициента b₂ по формуле (6.18)

Подставим b₁ и b₂ в уравнение (6.16)

у - 12,755 = -1,88,8(х₁- 0,0119) - 37,7(х₂- 0,0159),

отсюда

у = 15,6 - 188,8х₁- 37,7х₂.

Адекватность уравнения регрессии проверяется по критерию Фишера F_a (к₁, к₂) по методике, приведенной в 6.1.

7. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА ПРИ ПОИСКЕ ОПТИМАЛЬНЫХ УСЛОВИЙ

Планирование эксперимента - сравнительно новый метод подхода к постановке и проведению исследований и получил широкое применение для решения разнообразных задач: построения интерполяционных моделей, изучения кинетики и механизма явлений, оптимизации процессов и др.

Сущность методов планирования эксперимента состоит в том, что опыты проводятся по определенной схеме - матрице планирования.

Цель планирования эксперимента состоит в раздельном или одновременном решении задач двух типов. В первом случае исследователю необходимо решить задачу оптимизации, т.е. определить такие значения переменных факторов (х_i) для которых величина оптимизации (y) была бы максимальной или минимальной.

При решении задач второго типа исследователя интересует математическое описание влияния каждого фактора на функцию оптимизации.

Нередки случаи и слияния задач обоих типов, т.е. сначала определяют общий вид зависимости параметра оптимизации от переменных факторов, а затем выявляют оптимальные условия.

Важными этапами, предшествующими планированию эксперимента, являются выборы математической модели поверхности отклика, основного уровня для каждого фактора и интервалов его варьирования.

Математическая модель функции отклика необходима для нахождения кратчайшего пути достижения искомых параметров переменных факторов. Часто вид функции поверхности отклика неизвестен, поэтому ее аппроксимируют полиномом и ограничиваются линейными членами и взаимодействиями первого порядка

,                   (7.1)

где b₀, b_i, b_ij - выборочные коэффициенты регрессии;

y - целевая функция.

Выбор основного уровня и интервалов факторов проводится из имеющейся априорной информации (на основе анализа литературно-патентных данных).

Основной уровень - это наилучшие условия, установленные на основе анализа априорной информации, которым соответствует комбинация или несколько комбинаций уровней факторов.

Пример 7.1. Анализ литературно-патентной информации показал, что наилучшие свойства отливки из стали 15Л получаются при .заливке форм металлом с температурой 1560 °С. Это и будет основной уровень фактора "температура" при исследовании его влияния на свойства отливки. Таким же образом поступают и с другими факторами.

Основной уровень можно рассматривать как исходную точку для построения плана эксперимента, который сводится к выбору экспериментальных точек, симметричных относительно основного уровня (его еще называют нулевым). После выбора нулевого уровня необходимо установить интервалы варьирования факторов. Эта операция состоит в выборе для каждого фактора двух уровней, на которых он будет варьироваться в эксперименте, что выглядит следующим образом.

Представьте себе координатную ось, на которой откладываются значения данного фактора, в нашем примере температура заливки' стали 15Л в форму. Выбранный нами основной уровень равен 1560 °С. Это значение изображается точкой (рис. 7.1).

                         1530        1560        1590 t, ^оС

Рис.7.1. Схема к пояснению выбора интервалов варьирования

Тогда два интересующих нас уровня можно изобразить двумя точками, симметричными, относительно первой. Это соответственно верхний и нижний уровни.

Таким образом, интервалом варьирования называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, а вычитание - нижний уровни фактора.

Дня упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по осям выбираются так, чтобы верхний уровень соответствовал +1, нижний –1, а основной –0. Это всегда можно сделать с помощью кодирования

,                               (7.2)

где x_j - кодированное значение фактора;

- натуральное значение фактора;

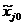- натуральное значение основного уровня;

J_j - интервал варьирования;

j - номер опыта.

В нашем случае это выглядит так:

; .

7.1. Полярный факторный эксперимент (ПФЭ) типа 2^к

Планирование эксперимента для получения линейной модели основано на варьировании факторов на двух уровнях. Если число факторов известно, можно сразу определить число опытов (N) необходимое для реализации всех возможных сочетаний уровней факторов

,                                        (7.3)

где N - число опытов;

к - число факторов;

2 - число уровней.

Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ). Матрица планирования для двух факторов в этом случае будет выглядеть следующим образом (табл. 7.1).

Таблица 7.1

Матрица планирования ПФЭ типа 2^к

Номер опыта

Факторы

ры

Отклик

у

х₁ х₂

1 -1 -1 у₁

2 +1 -1 у₂

3 -1 +1 у₃

4 +1 +1 у₄

S 0 0

Если для двух факторов все возможные комбинации уровней легко найти прямым перебором, то с ростом числа факторов возникает необходимость в некотором приеме построения матриц. Приемов таких несколько. Но наиболее широко используется прием, основанный на чередовании знаков. В первом столбце знаки меняются поочередно, во втором - через 2, в третьем - через 4, в четвертом - через 8 и т.д. по степеням двойки. В качестве примера в табл.7.2 приведена матрица планирования для ПФЭ 2³ (N = 8).

После построения матрицы, присыпают к проведении экспериментов. Причем каждый из опытов матрицы рекомендуется повторить 2-3 раза. Это будут параллельные опыты. Эксперименты следует проводить рандомизировано. Рандомизация осуществляется в основном с помощью таблиц случайных чисел. Результатом эксперимента будет служить модель вида (для матрицы табл.7.1)

у = b₀+b₁x₁+b₂x₂.                             (7.4)

                                        Таблица 7.2

Матрица планирования ПФЭ типа 2³

Номер опыта х₁ х₂ х₃ у

1 -1 -1 -1 у₁

2 +1 -1 -1 у₂

3 -1 +1 -1 у₃

4 +1 +1 -1 у₄

5 -1 -1 +1 у₅

6 +1 -1 +1 у₆

7 -1 +1 +1 у₇

8 +1 +1 +1 у₈

S 0 0 0

Для этого необходимо определить коэффициенты b₀, b₁, b₂ по формуле

, j = 0,1,…,к                (7.5)

где j – номер фактора (0 записан для вычисления b₀).

В нашем случае (табл. 7.1)

;                        (7.6)

;         (7.7)

;         (7.8)

Коэффициенты при независимых переменных указывают на силу влияния факторов. Чем больше численная величина коэффициента, тем большее влияние оказывает фактор на величину отклика. Если коэффициент имеет знак (+), то с увеличением значения фактора значение отклика увеличивается, а если (-) – уменьшается.

Полученная модель (7.4) является линейной. Но фактически в выбранных интервалах варьирования факторов процесс может изменяться и не по линейному закону. Как количественно оценить это?

Один из часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор, т.е. имеет место эффект взаимодействия двух факторов. Для того, чтобы получить столбец эффекта взаимодействия (например х₁х₂), необходимо перемножить построчно столбцы, принадлежащие факторам х₁ и х₂ (табл. 7.3)

Таблица 7.3

Матрица планирования ПФЭ 2² с эффектом взаимодействия

№ опыта х₁ х₂ х₁х₂ у

1 -1 -1 +1 у₁

2 +1 -1 -1 у₂

3 -1 +1 -1 у₃

4 +1 +1 +1 у₄

S 0 0 0

В этом случае математическая модель будет иметь вид

y=b₀+b₁x₁+b₂x₂+b₁₂x₁x₂.                    (7.9)

Расчет коэффициента b₁₂ производится так же, как b₁и b₂

.   (7.10)

При этом следует учесть, что опыты проводятся только по столбцам х₁, х₂, … , х_n. А столбцы взаимодействий факторов (х₁х₂, х₁х₃…х_1к) служат только для расчета. С ростом числа факторов число возможных взаимодействий быстро растет. Посмотрим на примере матрицы ПФЭ типа 2³ (табл. 7.4).

Столбец х₁х₂х₃ получается перемножением всех трех столбцов.

Модель

y=b₀+b₁x₁+b₂x₂+b₃x₃+b₁₂x₁x₂+b₁₃x₁x₃+b₂₃x₂x₃+b₁₂₃x₁x₂x₃. (7.11)

Расчет коэффициента b₁₂₃ ведется так же, как и всех остальных.

Эффект взаимодействия двух факторов x₁x₂ называется эффектом взаимодействия первого порядка, трех факторов - второго порядка и т.д.

Таблица 7.4

Матрица планирования ПФЭ типа 2³

с эффектами взаимодействия

№ х₁ х₂ х₃ х₁х₂ х₁х₃ х₂х₃ х₁х₂х₃ у

1 -1 -1 -1 +1 +1 +1 -1 у₁

2 +1 -1 -1 -1 -1 +1 +1 у₂

3 -1 +1 -1 -1 +1 -1 +1 у₃

4 +1 +1 -1 +1 -1 -1 -1 у₄

5 -1 -1 +1 +1 -1 -1 +1 у₅

6 +1 -1 +1 -1 +1 -1 -1 у₆

7 -1 +1 +1 -1 -1 +1 -1 у₇

8 +1 +1 +1 +1 +1 +1 +1 у₈

S 0 0 0 0 0 0 0

Количество опытов в ПФЭ значительно превосходит число определяемых коэффициентов линейной модели, т.е. ПФЭ обладает большой избыточностью опытов. Например, число опытов для ПФЭ типа 2³ N = 8, для 2⁴ N = 16 и т.д. Желательно уменьшить число опытов, при этом не потеряв смысла эксперимента. Это достигается при помощи планирования дробного факторного эксперимента.

7.2. Дробный факторный эксперимент (ДФЭ) типа 2^к-р

Обратимся еще раз к матрице планирования ПФЭ 2³ (см. табл. 7.4) и его математической модели 7.11. Если имеются основания считать, что в выбранных интервалах варьирования процесс может быть описан линейной моделью, то достаточно определить коэффициенты b₀, b₁, b₂, b₃. Остаются 4 степени свободы (все эффекты взаимодействия). При линейном приближении b₁₂®0; b₁₃®0; b₂₃®0; b₁₂₃®0, вектор столбцы х₁х₂, х₁х₃, х₂х₃, х₁х₂х₃ можно использовать для новых факторов х₄, х₅, х₆, х₇. И окажется, что вместо 128 опытов для ПФЭ 2⁷ можно провести всего 8 опытов. В этом состоит сущность дробного факторного эксперимента, который, как видно, реализует часть ПФЭ (дробную реплику). Дробные реплики получают, как мы установили, путем замены некоторых эффектов взаимодействия (или всех) на новые факторы. Число опытов ДФЭ находится по формуле

N=2^к-р,                                     (7.12)

где р – число взаимодействий в ПФЭ, замененное дополнительными факторами.

В табл. 7.5 показан пример матрицы планирования ДФЭ, где одно двойное и тройное взаимодействие х₁х₂х₃ в ПФЭ 2³ заменены на новые х₄ и х₅ факторы (N=2^5-2).

Модель

y=b₁x₁+b₂x₂+b₃x₃+b₄x₄+b₅x₅+b₁₃x₁x₃+b₂₃x₂x₃. (7.13)

Таким образом, 8 опытов позволяют оценить влияние 5 факторов, вместо 32 для ПФЭ 2⁵.

Таблица 7.5

Матрица планирования ДФЭ 2^5-2

№ опыта

Факторы

у

х₁ х₂ х₃ х₄ (х₁х₂) х₅ (х₁х₂х₃) х₁х₃ х₂х₃

1 -1 -1 -1 +1 -1 +1 +1 у₁

2 +1 -1 -1 -1 +1 -1 +1 у₂

3 -1 +1 -1 -1 +1 +1 -1 у₃

4 +1 +1 -1 +1 -1 -1 -1 у₄

5 -1 -1 +1 +1 +1 -1 -1 у₅

6 +1 -1 +1 -1 -1 +1 -1 у₆

7 -1 +1 +1 -1 -1 -1 +1 у₇

8 +1 +1 +1 +1 +1 +1 +1 у₈

S 0 0 0 0 0 0 0

После построения математической модели ее подвергают статистической проверке.

Воспроизводимость эксперимента при одинаковом количестве параллельных опытов проверяется по критерию Кохрена

,              (7.14)

где   - наибольшая из дисперсий у_i по каждой строке матрицы планирования;

- дисперсия у, полученная в i -м опыте;

a - уровень значимости, обычно принимается равным 0,05;

f_N - число степеней свободы, равное количеству опытов в матрице;

f_i   - число степеней свободы каждой оценки в i -ой строке плана, f_i = n-1, где n - число параллельных опытов;

G_p, G_т - расчетный и табличный критерии Кохрена.

Если условие 7.14 соблюдается, т.е. расчетный критерий Кохрена не превышает табличный (см прил. табл. 5, 6), то эксперимент воспроизводим. Другими словами, результаты эксперимента однородны и среди них нет грубых ошибок. При наличии грубых ошибок их необходимо сначала исключить, а затем проводить расчеты.

Значимость коэффициентов регрессии можно определить путем сравнения f - критериев Стьюдента - расчетного t_p и табличного t_т (см. прил. табл. 4)

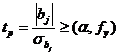,                           (7.15)

где b_j - численное значение коэффициента при факторах;

- среднее квадратическое отклонение коэффициента регрессии

,                                      (7.16)

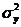- дисперсия воспроизводимости эксперимента;

N - число опытов по матрице;

n - число параллельных опытов,

в свою очередь

,                                      (7.17)

f_y -число степеней свободы, f_у = N (n - 1).

Все члены уравнения регрессии, при которых коэффициенты удовлетворяют условию (7.15) оставляют в модели, а незначимые отбрасывают. Однако при этом необходимо учитывать, что какой-либо коэффициент может оказаться незначимым из-за неправильно выбранного интервала варьирования. Поэтому статистическую значимость фактора необходимо оценить с технологической точки зрения.

Адекватность математической модели проверяют с помощью сравнения критериев Фишера - расчетного (F_р) и табличного (F_т) (см. прил., табл. 2).

,               (7.18)

где - дисперсия адекватности модели

,               (7.19)

d - число членов в модели после проверки значимости         коэффициентов;

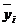  - среднее значение отклика в катком опыте;

- расчетное значение отклика по полученному уравнению регрессии для каждого опыта;

f_ад - число степеней свободы, f_ад = N-d;

f_y - число степеней свободы, f_y = N(n-1).

При соблюдении условия (7.18) полученная математическая модель будет адекватной. В случае неадекватности модели необходимо переходить к более сложной форме математического описания (плана второго порядка и др.) либо, если это возможно, проводить эксперимент с меньшим интервалом варьирования факторов.

В подученной адекватной модели коэффициенты регрессии и их знаки показывают, как изменяется значение отклика, если соответствующий фактор изменить на величину одного интервала варьирования.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Основы научных исследований в литейном производстве /А.Е.Кривошеев, Г.Е.Белай, Г.Ш.Кирия и др. Киев - Донецк: Вища школа, 1979.186 с.

2. Зайдель А.Н. Ошибки измерений физических величин. Л.: Наука, 1974. 108 с.

3. Кнотек М., Вайта Р., Шефц И. Анализ металлургических процессов методами математической статистики. М.: Металлургия, 1968. 212 c.

4. Ахназарова С.Л., Кафаров В.В. Оптимизация эксперимента в химии и химической технологии. М.: Высш. шк., 1978. 319 с.

5. Красовский Г.И., Филаретов Г.Ф. Планирование эксперимента. Л.:    БГУ, 1982. 302 с.

6. Новак О.С., Арсов Н.Б. Оптимизация процессов технологии металлов методами планирования экспериментов. М.: Машиностроение; София: Техника, 1980. 304 с.

7. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1979. 260 с.

8. Математическая статистика: Учебник /В.М.Иванова, В.Н.Калинина,Л.А.Нешумова, И.О.Решетникова. М.: Высш. шк., 1981. 371 с.

ПРИЛОЖЕНИЕ

Таблица 1

Критические значения критерия Фишера F_1-_a для a = 0,05

f₂

f₁

1 2 3 4 5 6 7 8 9

1 161 200 216 225 230 234 237 239 242

2 18,51 19,0 19,16 19,25 19,30 19,33 19,36 19,37 19,38

3 10,13 9,55 9,28 9,12 9,01 8,94 8,84 0,84 8,81

4 7,71 6,94 6,59 6,39 6,26 6,16 6,09 6,04 6,00

5 6,61 5,79 5,41 5,19 5,05 4,95 4,00 4,02 4,70

6 5,99 5,14 4,76 4,53 4,39 4,28 4,21 4,15 4,10

7 5,59 4,74 4,35 4,12 3,97 3,67 3,79 3,73 3,68

8 5,32 4,46 4,07 3,04 3,69 3,58 3,50 3,44 3,39

9 5,12 4,26 3,86 3,63 3,40 3,37 3,29 3,23 3,18

10 4,96 4,10 3,71 3,48 3,33 3,22 3,14 3,07 3,02

11 4,84 3,98 3,59 3,36 3,20 3,09 3,01 2,95 2,90

12 4,75 3,88 3,49 3,26 3,11 3,00 2,92 2,85 2,80

13 4,67 3,80 3,41 3,18 3.02 2,92 2,84 2,77 2,72

14 4,60 3,74 3,34 3,11 2,96 2,85 2,77 2,70 2,65

15 4,54 3,68 3,29 3,06 2,90 2,79 2,70 2,64 2,59

16 4,49 3,63 3,24 3,01 2,85 2,74 2,66 2,59. 2,54

17 4,45 3,59 3,20 2,96 2,81 2,70 2,62 2,55 2,50

18 4,38 3,55 3,16 2,93 2,70 2,66 2,58 2,51 2,46

Таблица 2

Критические значений критерия Фишера F_1-_a для a = 0,01

f₂

f₁

1 2 3 4 5 6 7 8 9 10

1 4052 4999 5403 5625 5764 5859 5928 5982 6022 6056

2 98,49 99,01 99,17 99,25 99,30 99,33 99,34 99,36 99,38 99,40

3 34,12 30,81 29,46 26,71 28,24 27,91 27,67 27,49 27,34 27,23

4 21,20 18,00 16,69 15,98 15,52 15,21 14,98 14,80 14,66 14,54

5 16,26 13,27 12,06 11,39 10,97 10,67 10,45 10,29 10,15 10,05

6 13,74 10,92 9,78 9,15 8,75 8,47 8,26 8,10 7,98 7,87

7 12,25 9,55 8,45 7,85 7,46 7,19 7,00 6,84 6,71 6,62

8 11,26 8,65 7,59 7,01 6,63 6,37 6,19 6,03 5,91 5,82

9 10,56 8,02 6,99 6,42 6,06 5,80 5,62 5,47 5,35 5,26

10 10,04 7,56 6,55 5,99 5,64 5,39 5,21 5,06 4,95 4,85

11 9,65 7,20 6,22 5,67 5,32 5,07 4,88 4,74 4,63 4,54

12 9,33 6,93 5,95 5,41 5,06 4,82 4,65 4,50 4,39 4,30

13 9,07 6,70 5,74 5,20 4,86 4,63 4,44 4,30 4,19 4,10

14 8,86 6,51 5,56 5,03 4,69 4,46 4,28 4,14 4,03 3,94

15 8,68 6,36 5,42 4,89 4,56 4,32 4,14 4,00 3,89 3,80

16 8,53 6,23 5,29 4,77 4,44 4,20 4,03 3,89 3,78 3,69

17 8,40 6,11 5,18 4,67 4,34 4,10 3,93 3,79 3,68 3,59

18 8,28 6,01 5,09 4,58 4,25 4,01 3,85 3,71 3,60 3,51

Таблица 3

Критические значения коэффициента корреляции

Дата добавления: 2018-05-02; просмотров: 572; Мы поможем в написании вашей работы!
Поделиться с друзьями:

Мы поможем в написании ваших работ!

12	17	15	12	14	15	14	17	13
14	16	16	13	15	15	15	16	16
13	12	14	16	15	15	15	16	16
16	13	14	16	16	16	16	16	13
14	15	13	14	14	16	15	17	17

Признак группирования	Частота n_i	Относительная частота f_i.	Кумулятивная абсолютная частота	Кумулятивная относительная частота
12	3	0,067	3	0,067
13	6	0,133	9	0,200
14	8	0,178	17	0,378
15	10	0,222	27	0,600
16	14	0,311	41	0,911
17	4	0,089	45	1,000
S	45	1,000	-	-

0,35	0,36	0,30	0,34	0,33	0,35	0,37	0,38
0,35	0,35	0,35	0,35	0,35	0,36	0,37	0,35
0,36	0,30	0,34	0,35	0,38	0,35	0,35	0,46
0,34	0,31	0,33	0,36	0,38	0,41	0,36	0,35
0,32	0,31	0,34	0,37	0,40	0,41	0,37	0,36
0,35	0,32	0,33	0,37	0,39	0,40	0,36	0,35
0,35	0,32	0,35	0,42	0,39	0,38	0,35	0,42
1	2	3	4	5	6	7	8

Граница групп	Середина интервала	Частота n_i	Относительная частота f_i	Кумулятивная абсолютная частота	Кумулятивная относительная частота
0,30-0,32	0,31	4	0,071	4	0,071
0,32-0,34	0,33	6	0,107	10	0,178
0,34-0,36	0,35	22	0,393	32	0,671
0,36-0,38	0,37	11	0,196	43	0,767
0,38-0,40	0,39	6	0,107	49	0,874
0,40-0,42	0,41	4	0,071	53	0,945
0,42-0,44	0,43	2	0,036	55	0,981
0,44-0,46	0,45	1	0,018	56	1,000
S		56	1,000

Номер испытания	Уровни фактора
i	А₁	А₂	…	А_к
1	У₁₁	У₁₂	…	У_1к
2	У₂₁	У₂₂	…	У_2к
…	…	…	…	…
n	У_n1	У_n2	...	У_nк
N			…

Номер испытания i	Уровни фактора
Номер испытания i	А₁	А₂	А₃
1	38	20	21
2	36	24	22
3	35	26	31
4	31	30	34
	35	25	27

Номер испытания i	Уровни фактора						Итоговый столбец
	F₁		F₂		F₃
	Х_i1	Х²_i1	Х_i2	Х²_i2	Х_i3	Х²_i3
1	9	81	-9	81	-8	64
2	7	49	-5	25	-7	49
3	6	36	-3	9	2	4
4	2	4	1	1	5	25
		170		116		142
	24		-16		-8
	576		256		64

Номер испытания i	Уровни фактора
Номер испытания i	A₁	A₂	A₃	A₄
1	1,38	1,41	1,32	1,31
2	1,38	1,42	1,33	1,33
3	1,42	1,44	1,34	-
4	1,42	1,45	-	-
Групповая средняя	1,40	1,43	1,33	1,32

В	А				Итого
В	а₁	а₂	…	а_к	Итого
в₁	у₁₁	у₁₂	…	у_к1	В₁
в₂	у₂₁	у₂₂	…	у_к2	В₂
…	…	…	…	…	…
в_m	у_m1	у_m2	…	у_mк	В_m
Итого	А₁	А₂	…	А_к

Источник дисперсии	Число степеней свободы	Сумма квадратов	Средний квадрат
А	к – 1
В	m – 1
Остаток	(к – 1)(m – 1)
Общая сумма	кm - 1

12	17	15	12	14	15	14	17	13
14	16	16	13	15	15	15	16	16
13	12	14	16	15	15	15	16	16
16	13	14	16	16	16	16	16	13
14	15	13	14	14	16	15	17	17

В (температура отпуска, ^оС)	А (температура закалки, ^оС)
	а₁	а₂	а₃
	880	930	980
в₁ 570	401 403	415 417	428 430
в₂ 620	361 363	362 364	363 365
в₃ 670	321 323	339 341	353 351

В	А			Итоги
В	а₁	а₂	а₃	Итоги
в₁	804	832	858	2494
в₂	724	726	728	2178
в₃	644	680	704	2028
Итоги	2172	2238	2290	6700

№	Содержание титана, % Хi	Предел прочности, Мпа	(x_i-x)	(x_i-x)²	(y_i-y)	(y_i-y)²	ху*
1	0,025	290	-0,0254	0,0006	-30,385	923,225	7,25
2	0,03	295	-0,0204	0,0004	-25,385	644,379	8,85
3	0,032	290	-0,0184	0,0003	-30,385	923,225	9,28
4	0,04	310	-0,0104	0,0001	-10,385	107,840	12,4
5	0,046	320	-0,0044	0,0000	-0,385	0,148	14,72
6	0,048	315	-0,0024	0,0000	-5,385	28,994	15,12
7	0,05	323	-0,0004	0,0000	2,615	6,840	16,15
8	0,054	330	0,0036	0,0000	9,615	92,456	17,82
9	0,056	324	0,0056	0,0000	3,615	13,071	18,144
10	0,06	345	0,0096	0,0001	24,615	605,917	20,7
11	0,07	330	0,0196	0,0004	9,615	92,456	23,1
12	0,072	338	0,0216	0,0005	17,615	310,302	24,336
13	0,072	355	0,0216	0,0005	34,615	1198,225	25,56
S	0,655	4165	0	0,0030	0	4947,077	213,43

	1	2	3	4	5	6	7	8
Х	1,5	4,0	5,0	7,0	8,5	10,0	11,0	12,5
У	5,0	4,5	7,0	6,5	9,5	9,0	11,0	9,0

№	х²	у²	ху	х+у	(х+у)²
1	2,25	25,00	7,50	6,50	42,25
2	16,00	20,25	18,00	8,50	72,25
3	25,00	49,00	35,00	12,00	144,00
4	49,00	42,25	45,50	13,50	182,25
5	72,25	90,25	80,75	18,00	324,00
6	100,00	81,00	90,00	19,00	361,00
7	121,00	121,00	121,00	22,00	484,00
8	156,25	81,00	112,50	21,50	462,25
S	541,75	509,75	510,25	121,00	2072,00

№	Средние размеры графитовых включений хi, мкм	Твердость серого чугуна по Бриннелю уi, МПа	(x_i-x)	(x_i-x)²	(y_i-y)	(y_i-y)²	ху*
1	104	187	-11,667	136,111	1,75	3,063	19448
2	99	184	-16,667	277,778	-1,25	1,563	18216
3	108	192	-7,667	58,778	6,75	45,563	20736
4	100	187	-15,667	245,444	1,75	3,063	18700
5	110	179	-5,667	32,111	-6,25	39,063	19690
6	120	180	4,333	18,778	-5,25	27,563	21600
7	144	170	28,333	802,778	-15,25	232,563	24480
8	198	161	82,333	6778,778	-24,25	588,063	31878
9	153	180	37,333	1393,778	-5,25	27,563	27540
10	90	200	-25,667	658,778	14,75	217,563	18000
11	83	201	-32,667	1067,111	15,75	248,063	16683
12	79	202	-36,667	1344,444	16,75	280,563	15958
S	1388	2223	0	12814,667	0	1714,250	252929

№	х_i	у_i
1	104	187	220,1 - 0,3 × 104 = 188,9	-1,9	3,81
2	99	184	220,1 - 0,3 × 99 = 190,3	-6,3	39,6
3	106	192	220,1 - 0,3 × 108 = 187,7	+4,3	17,4
4	100	187	220,1 - 0,3 × 100 = 190,1	-3,1	9,6
5	110	179	220,1 - 0,3 × 110 = 187,1	-8,1	64,9
6	120	180	220,1 - 0,3 × 120 = 184,1	-4,1	16,8
7	144	170	220,1 - 0,3 × 144 = 176,9	-6,9	47,6
8	198	161	220,1 - 0,3 × 198 = 158,4	+2,6	6,3
9	153	180	220,1 - 0,3 × 153 = 174,2	+5,8	33,6
10	90	200	220,1 - 0,3 × 90 = 193,1	+6,9	47,6
11	83	201	220,1 - 0,3 × 83 = 195,2	+5,8	33,6
12	79	202	220,1 - 0,3 × 79 = 196,4	+5,6	31,3
					353,2

Номер опыта	Факторы ры		Отклик у
Номер опыта	х₁	х₂	Отклик у
1	-1	-1	у₁
2	+1	-1	у₂
3	-1	+1	у₃
4	+1	+1	у₄
S	0	0

№ опыта	х₁	х₂	х₁х₂	у
1	-1	-1	+1	у₁
2	+1	-1	-1	у₂
3	-1	+1	-1	у₃
4	+1	+1	+1	у₄
S	0	0	0

12	17	15	12	14	15	14	17	13
14	16	16	13	15	15	15	16	16
13	12	14	16	15	15	15	16	16
16	13	14	16	16	16	16	16	13
14	15	13	14	14	16	15	17	17

№	х₁	х₂	х₃	х₁х₂	х₁х₃	х₂х₃	х₁х₂х₃	у
1	-1	-1	-1	+1	+1	+1	-1	у₁
2	+1	-1	-1	-1	-1	+1	+1	у₂
3	-1	+1	-1	-1	+1	-1	+1	у₃
4	+1	+1	-1	+1	-1	-1	-1	у₄
5	-1	-1	+1	+1	-1	-1	+1	у₅
6	+1	-1	+1	-1	+1	-1	-1	у₆
7	-1	+1	+1	-1	-1	+1	-1	у₇
8	+1	+1	+1	+1	+1	+1	+1	у₈
S	0	0	0	0	0	0	0

№ опыта	Факторы							у
№ опыта	х₁	х₂	х₃	х₄ (х₁х₂)	х₅ (х₁х₂х₃)	х₁х₃	х₂х₃	у
1	-1	-1	-1	+1	-1	+1	+1	у₁
2	+1	-1	-1	-1	+1	-1	+1	у₂
3	-1	+1	-1	-1	+1	+1	-1	у₃
4	+1	+1	-1	+1	-1	-1	-1	у₄
5	-1	-1	+1	+1	+1	-1	-1	у₅
6	+1	-1	+1	-1	-1	+1	-1	у₆
7	-1	+1	+1	-1	-1	-1	+1	у₇
8	+1	+1	+1	+1	+1	+1	+1	у₈
S	0	0	0	0	0	0	0