Пример использования непараметрических критериев (НК)
СЕМИНАР №6
Непараметрические статистические критерии
При проведении классификации возникает задача корректного сравнения точности различных решающих правил. Чаще всего необходимо ответить на вопрос: обеспечивает ли один метод на различных выборках систематическое улучшение точности или нет?
Казалось бы, логичным для снятия неопределенности использовать специальные статистические критерии. Однако для ошибок методов классификации обычно не соблюдаются предположения о нормальном законе распределения и однородности дисперсий. Кроме того, точность классификаторов обычно оценивается по небольшому числу выборок. В связи с этим представляется нецелесообразным использовать классические параметрические критерии (например, t-критерий или ANOVA) и их модификации, которые разработаны для частичной компенсации отклонений от исходных предположений. Для корректного сопоставления классификаторов более продуктивно применять непараметрические тесты.
Уточним постановку задачи: имеется совокупность выборок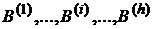 
(i = 1,…, h, h – количество выборок), на этих выборках проводится классификация с помощью группы решающих правил 
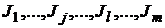(j,l = 1,…,m, m- количество решающих правил). Обычно один метод (или несколько методов) в группе является новым (или модифицированным), именно его точностные характеристики должны быть установлены по отношению к остальным базовым классификаторам, принимающим участие в исследовании. При этом цели сравнительного анализа формулируются следующим образом:
|
|
|
1) необходимо сопоставить точность двух классификаторов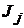 
и 
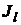, а также установить, насколько значимо улучшает (или не улучшает) точность классификации один из методов;
2) необходимо сопоставить точность всех решающих правил и установить, имеются ли статистически значимые различия в их точности.
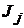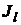Рассмотрим применение непараметрических критериев для сопоставления точности двух классификаторов и . Для определенности будем считать, что 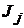- вновь разработанный классификатор, а 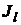- базовый классификатор. Формализуем решаемую задачу. Имеются две связанные выборки одинакового размера. Первая состоит из ошибок 
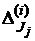, полученных на группе выборок 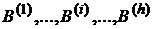(i=1,…,h) с помощью решающего правила 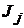(т.е. 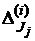- - число элементов выборки B(i), неправильно классифицированных с помощью решающего правила 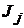). Вторая выборка содержит ошибки 
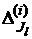, сделанные решающим правилом 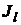. Ошибки 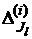получены на тех же выборках .
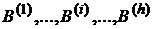Речь идет о проверке однородности связанных выборок. Проверяется нулевая гипотеза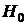 
о том, что две связанные выборки, каждая из которых состоит из ошибок одного из методов, принадлежат однородным генеральным совокупностям, их функции распределения совпадают. Фактически 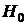означает, что изменение ошибок классификации за счет использования вновь разработанного метода 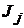носит случайный характер, альтернативная гипотеза 
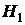предполагает, что ошибки новой процедуры систематически отличаются от ошибок базового метода 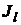. В качестве альтернативной гипотезы часто рассматривают «гипотезу сдвига».
|
|
|
Рассчитаем разности элементов связанных выборок:
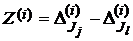. (1)
Общая математическая модель для проведения статистического оценивания имеет вид:
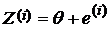, (2)
где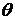 
- неизвестный параметр, характеризующий различие в точности двух классификаторов, 
- ненаблюдаемые случайные величины, которые являются независимыми и принадлежат непрерывной совокупности, симметричной относительно нуля.
Таким образом, приведенная выше модель предполагает, что значения разностей определяются двумя составляющими: закономерной и случайной. При проведении статистического оценивания нас в первую очередь интересует закономерная составляющая, величина которой предопределяется действием некоторого числа скрытых причин, прежде всего качеством настройки параметров решающих правил, их обобщающей мощностью. В случае, если решающие правила 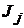и 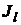обладают идентичными точностными характеристиками, то 
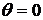, различия в разностях случайны, 
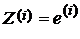и эффект выигрыша в точности от использования одного из классификаторов отсутствует.
|
|
|
Из непараметрических критериев для решения поставленной задачи рассмотрим критерий знаков и критерий знаковых рангов Вилкоксона для связанных выборок (Wilcoxon Watched Pair Test).
Критерий знаков основывается на расчете случайных величин, представляющих разность элементов связанных выборок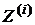 
(см. формулу (2)). Нулевые разности, возникающие из-за случайных погрешностей и ошибок округления и соответствующие им пары наблюдений, исключим из рассмотрения. В случае, если значимых различий в точности классификаторов нет, то вероятности появления положительных и отрицательных разностей равны 
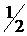. Таким образом, в критерии знаков проверяется гипотеза:
.
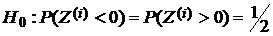Соответствующая альтернативная гипотеза имеет вид:
.
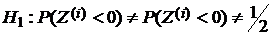Здесь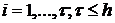 
, 
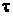- количество ненулевых разностей.
Статистикой критерия является число знаков «+» (или «-») величины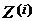 
. В дальнейшем для определенности берется число знаков «+». При условии, что гипотеза 
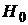верна, знаки разности 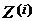- независимы и число знаков «+» имеет биномиальное распределение с параметрам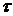и 
и .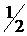
|
|
|
Пусть r– наблюденное число знаков «+», а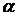 
- заданный уровень значимости. Гипотеза 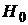отклоняется для двустороннего критерия, если выполняется одно из неравенств:
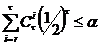, или 
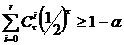. (3)
Если данные неравенства не выполняются, то гипотеза 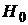не противоречит результатам наблюдений и принимается на уровне значимости 
.
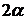Для определения статистики критерия используются таблицы биномиального распределения, а также нормальная аппроксимация биноминального распределения:
.
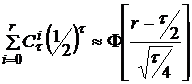Здесь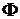 
- функция стандартного нормального распределения 
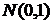. Из теоремы Муавра-Лапласа следует правило принятия решений на уровне значимости 5%. Если
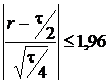, (4)
то нулевую гипотезу принимают, в противном случае отклоняют (для другого уровня значимости в качестве критического значения выбирается иная квантиль нормального распределения).
Критерий знаковых рангов Вилкоксона (далее критерий Вилкоксона), в отличие от критерия знаков, основывается на расчете рангов. Модули разностей между ошибками сравниваемых методов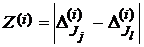 
, вычисленные по связанным выборкам, упорядочиваются в порядке возрастания и им присваивается ранг (от 1 до τ). Поскольку значения разностей случайны, случайными величинами оказываются и их ранги. При справедливости нулевой гипотезы для непрерывного и симметричного распределения случайной составляющей (см. формулу (2)) все ранговые последовательности оказываются равновероятными и независящими от конкретного вида закона распределения . Выборочная статистика критерия Вилкоксона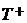 
равна сумме рангов положительных разностей. В случае, если исследуемые выборки имеют небольшой размер (τ<25), тодля определения 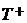используются специальные таблицы [15]: 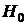отклоняется на уровне 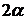, если
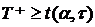или 
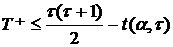. (5)
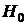принимается на уровне 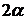, если
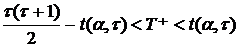. (6)
При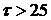 
используют статистику 
:
.
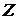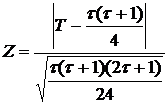При условии, что гипотеза 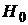верна, 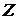имеет (приближенно) стандартное нормальное распределение 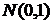. Гипотеза 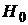отклоняется при двухсторонней альтернативе на уровне значимости 5%, если
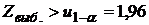, (7)
где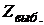 
- выборочное значение статистики , 
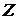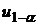- квантиль стандартного нормального распределения .
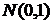Критерий Фридмана используется для сопоставления точности трех и более классификаторов по связанным выборкам. Критерий Фридмана (Friedman Test) – непараметрический аналог однофакторного дисперсионного анализа (ANOVA). Предположим, что в исследовании на группе выборок 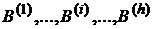(i = 1,…,h) испытываются классификаторы (алгоритмы классификации) 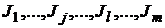(j,l = 1,…,m) и проверяется наличие различий в обработке (т.е. отличий в ошибках классификации). Математическая модель для проведения статистического оценивания имеет вид:
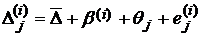, (8)
где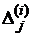 
- ошибка классификатора 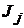на выборке 
; 
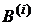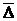- неизвестная средняя ошибка классификаторов на всех (возможных) выборках; 
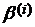- неизвестные параметры, которые отражают «эффект выборки», т.е. погрешности возникающие из-за структуры конкретной выборки; 
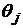- неизвестный параметр, характеризующий точность классификатора 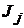(наличие «эффекта обработки» от использования этого метода); 
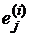- ненаблюдаемые случайные взаимно независимые величины, извлеченные из непрерывной совокупности. Проверяется нулевая гипотеза о том, что «эффект обработки» отсутствует (методы обеспечивают идентичную точность) против альтернативы, что не все классификаторы эквивалентны:
,
.
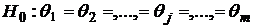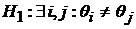Для проверки гипотезы необходимо сделать следующие расчеты.
1. Проводится ранжирование точности классификаторов для каждой выборки. Классификатор, который показал наилучшую точность на выборке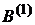 
получает ранг 1, следующий по точности классификатор (на выборке 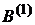) - ранг 2, наименее точный классификатор (на выборке 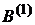) - ранг m. Аналогичное упорядочивание проводится для остальных (h-1) выборках.
2. Для каждого классификатора определяется сумма рангов по всем выборкам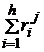 
и средний ранг 
( 
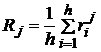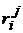- ранг j–го классификатора на i–ой выборке).
3. Вычисляется выборочная статистика Фридмана
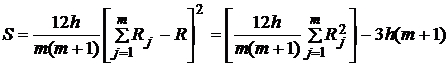. (9)
Здесь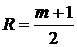 
.
4. Гипотеза 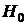отклоняется на уровне 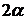, есл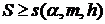и 
, и 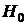принимается на уровне 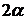, если 
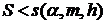. Константы 
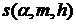определяются по специальным таблицам.
В случае h>10 и m>5 можно воспользоваться тем, что данная статистика имеет асимптотическое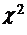 
распределение с (m-1) степенью свободы. Тогда
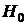отклоняется на уровне 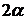, если 
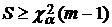, (10)
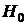принимается на уровне 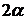, если 
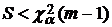. (11)
Чем сильнее различаются классификаторы по точности, тем большие значения будут принимать значения выборочной статистики Фридмана, и, наоборот, меньшие значения статистики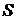 
будут соответствовать случаю, когда значения 
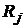близки к .
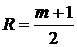При отклонении 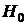принимается альтернативная гипотеза без конкретизации направлений различий. Для получения более детальных выводов необходимо использовать дополнительные тесты, например, критерий Пейджа или критерий Вилкоксона. В некоторых публикациях рассматривается также возможность использования наряду (вместо) с критерием Фридмана непараметрического теста Кендалла, в котором в качестве статистики применяется коэффициент конкордации (см. семинар 1).
Критерий Пейджа применяют для проверки 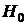против альтернативы
,
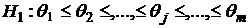где хотя бы одно неравенство строгое. При этом необходимо выполнить следующие расчеты.
1. Вычислить выборочную статистику
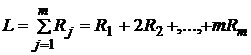, (12)
где ранги 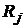рассчитываются аналогично тому, как это делалось в критерии Фридмана.
2. Гипотеза 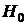отклоняется на уровне 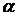, есл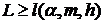и 
, и 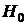принимается на уровне 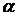, если 
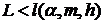. Константы 
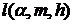определяется по специальным таблицам [15].
Для больших выборок статистика Пейджа имеет асимптотическое нормальное распределение .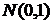
Пример использования непараметрических критериев (НК)
Рассмотрим процедуру анализа точности классификаторов с помощью непараметрических критериев на примере обработки текстовых данных. На девяти выборках, сформированных из различных документальных библиографических БД и имеющих одинаковую структуру (размер и число классов), испытывалось 4 метода классификации. Три классификатора (метод центроидов (МЦ), метод к-ближайших соседей (метод к-БС) и наивный байесовский метод (НБМ)), относятся к числу широко известных и хорошо изученных процедур. Еще один метод классификатор, модифицированный метод ближайшего соседа (ММБС), является модификацией метода к-ближайших соседей, в которой за счет введения ряда эвристик удается увеличить быстродействие.
Целями использования непараметрических критериев являются:
- установить имеются ли значимые различия в точности при применении различных методов классификации (т.е. присутствует «эффект обработки»);
- определить имеются ли существенные потери в точности в модифицированном методе по отношению к прототипу - методу к-БС.
Ошибки испытываемых классификаторов на девяти выборках приведены в табл.1.
Таблица 1
Дата добавления: 2018-05-02; просмотров: 58; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!