Разыгрывание дискретной случайной величины.
Обозначим равномерно распределенную СВ в интервале (0, 1) через R, а ее возможные значения (случайные числа) - rj.
Разобьем интервал [0, 1) точками с координатами р1, р1+р2, , р1+р2+р3, …, р1+р2+р3 +…+рn-1 на n частичных интервалов :
 .
.
Длина каждого из них равна вероятности рi.
Далее поступаем так: выбираем из таблицы случайных чисел какое –либо случайное число rj, если оно попало в интервал i , то разыгрываемая СВ приняла возможное значение хi.
ЛЕКЦИЯ 12. АЛГОРИТМЫ НА ГРАФАХ.
ОБХОДЫ ГРАФА (ПОИСК В ГРАФЕ)
Цели и задачи лекции: Изучить методы поиска в графе.
Рассматриваемые вопросы: Поиск в ширину. Поиск в глубину.
Язык графов оказывается удобным для описания многих физических, технических, экономических, биологических, социальных и других систем.
Примеры приложений теории графов.
1. «Транспортные» задачи, в которых вершинами графа являются пункты, а ребрами - дороги (автомобильные, железные и др.) и/или другие транспортные (например, авиационные) маршруты. Другой пример - сети (информационные, энергоснабжения, газоснабжения, снабжения товарами и т.д.), в которых вершинами являются пункты производства (источники) и потребления (получатели), а ребрами – возможные маршруты перемещения (линии электропередач, газопроводы, дороги и т.д.). Соответствующий класс задач оптимизации потоковгрузов, размещения пунктов производства и потребления и т.д., иногда называется задачами обеспечения или задачами о размещении. Их подклассом являются задачи о грузоперевозках.
|
|
|
2. «Технологические задачи», в которых вершины отражаютпроизводственные элементы (заводы, цеха, станки и т.д.), а дуги -потоки сырья, материалов и продукции между ними, заключаются в определении оптимальной загрузки производственных элементов и обеспечивающих эту загрузку потоков.
3. Обменные схемы, являющиеся моделями таких явлений какбартер, взаимозачеты и т.д. Вершины графа при этом описываютучастников обменной схемы (цепочки), а дуги - потоки материальных и финансовых ресурсов между ними. Задача заключается вопределении цепочки обменов, оптимальной с точки зрения, например, организатора обмена и согласованной с интересами участников цепочки и существующими ограничениями.
4. Управление проектами. С точки зрения теории графов проект - совокупность операций и зависимостей между ними {сетевой график). Хрестоматийным примером является проектстроительства некоторого объекта. Совокупность моделей и методов, использующих язык и результаты теории графов и ориентированных на решение задач управления проектами, получила название календарно-сетевого планирования и управления (КСПУ). В рамках КСПУ решаются задачи определения последовательности выполнения операций и распределения ресурсов междуними, оптимальных с точки зрения тех или иных критериев (времени выполнения проекта, затрат, риска и др.).
|
|
|
5. Модели коллективов и групп, используемые в социологии,основываются на представлении людей или их групп в виде вершин, а отношений между ними (например, отношений знакомства,доверия, симпатии и т.д.) - в виде ребер или дуг. В рамках подобного описания решаются задачи исследования структуры социальных групп, их сравнения, определения агрегированных показателей, отражающих степень напряженности, согласованностивзаимодействия, и др.
6. Модели организационных структур, в которых вершинамиявляются элементы организационной системы, а ребрами или дугами - связи (информационные, управляющие, технологическиеи др.) между ними.
Рассмотрим задачаи анализа графов с целью выявления их структуры и вычисления метрических характеристик. Многие задачи такого рода могут быть решены путем систематического обхода графа с посещением всех его вершин и исследованием всех его ребер.
Процедура поиска в ширину
Работа всякого алгоритма обхода состоит в последовательном посещении вершин и исследовании ребер. Какие именно действия выполняются при посещении вершины и исследовании ребра - зависит от конкретной задачи, для решения которой производится обход. В любом случае, однако, факт посещения вершины запоминается, так что с момента посещения и до конца работы алгоритма она считается посещенной. Вершину, которая еще не посещена, будем называть новой. В результате посещения вершина становится открытой и остается такой, пока не будут исследованы все инцидентные ей ребра. После этого она превращается в закрытую.
|
|
|
Идея поиска в ширину состоит в том, чтобы посещать вершины в порядке их удаленности от некоторой заранее выбранной или указанной стартовой вершины 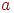 . Иначе говоря, сначала посещается сама вершина
. Иначе говоря, сначала посещается сама вершина 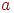 , затем все вершины, смежные с
, затем все вершины, смежные с 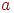 , то есть находящиеся от нее на расстоянии
, то есть находящиеся от нее на расстоянии  , затем вершины, находящиеся от
, затем вершины, находящиеся от 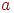 на расстоянии
на расстоянии  , и т.д.
, и т.д.
Рассмотрим алгоритм поиска в ширину с заданной стартовой вершиной 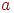 . Вначале все вершины помечаются как новые. Первой посещается вершина
. Вначале все вершины помечаются как новые. Первой посещается вершина 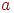 , она становится единственной открытой вершиной. В дальнейшем каждый очередной шаг начинается с выбора некоторой открытой вершины
, она становится единственной открытой вершиной. В дальнейшем каждый очередной шаг начинается с выбора некоторой открытой вершины  . Эта вершина становится активной. Далее исследуются ребра, инцидентные активной вершине. Если такое ребро соединяет вершину
. Эта вершина становится активной. Далее исследуются ребра, инцидентные активной вершине. Если такое ребро соединяет вершину  с новой вершиной
с новой вершиной 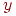 , то вершина
, то вершина 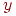 посещается и превращается в открытую. Когда все ребра, инцидентные активной вершине, исследованы, она перестает быть активной и становится закрытой. После этого выбирается новая активная вершина, и описанные действия повторяются. Процесс заканчивается, когда множество открытых вершин становится пустым.
посещается и превращается в открытую. Когда все ребра, инцидентные активной вершине, исследованы, она перестает быть активной и становится закрытой. После этого выбирается новая активная вершина, и описанные действия повторяются. Процесс заканчивается, когда множество открытых вершин становится пустым.
|
|
|
Основная особенность поиска в ширину, отличающая его от других способов обхода графов, состоит в том, что в качестве активной вершины выбирается та из открытых, которая была посещена раньше других. Именно этим обеспечивается главное свойство поиска в ширину: чем ближе вершина к старту, тем раньше она будет посещена. Для реализации такого правила выбора активной вершины удобно использовать для хранения множества открытых вершин очередь - когда новая вершина становится открытой, она добавляется в конец очереди, а активная выбирается в ее начале. Схематически процесс изменения статуса вершин изображен на рис.1.

Рис. 1.
Опишем процедуру поиска в ширину (BFS - от английского названия этого алгоритма - Breadth First Search) из заданной стартовой вершины 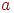 . В этом описании
. В этом описании  обозначает множество всех вершин, смежных с вершиной
обозначает множество всех вершин, смежных с вершиной  ,
,  - очередь открытых вершин. Предполагается, что при посещении вершины она помечается как посещенная и эта пометка означает, что вершина уже не является новой.
- очередь открытых вершин. Предполагается, что при посещении вершины она помечается как посещенная и эта пометка означает, что вершина уже не является новой.
Procedure BFS(a)
1.посетить вершину 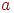
2. 
3.while 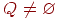 do
do
4. 
5.for 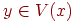 do
do
6.исследовать ребро 
7.if вершина 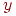 новая
новая
8.then посетить вершину 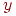
9. 
Отметим некоторые свойства процедуры BFS.
1.Процедура BFS заканчивает работу после конечного числа шагов.
Действительно, при каждом повторении цикла while из очереди удаляется одна вершина. Вершина добавляется к очереди только тогда, когда она посещается. Каждая вершина может быть посещена не более одного раза, так как посещаются только новые вершины, а в результате посещения вершина перестает быть новой. Таким образом, число повторений цикла while не превосходит числа вершин.
2.В результате выполнения процедуры BFS будут посещены все вершины из компоненты связности, содержащей вершину a, и только они.
Очевидно, что вершина может быть посещена только в том случае, когда существует путь, соединяющий ее с вершиной 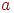 (так как посещается всегда вершина, смежная с уже посещенной). То, что каждая такая вершина будет посещена, легко доказывается индукцией по расстоянию от данной вершины до вершины
(так как посещается всегда вершина, смежная с уже посещенной). То, что каждая такая вершина будет посещена, легко доказывается индукцией по расстоянию от данной вершины до вершины 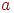 .
.
3.Время работы процедуры BFS есть 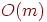 , где
, где  - число ребер в компоненте связности, содержащей вершину
- число ребер в компоненте связности, содержащей вершину 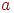 .
.
Из предыдущих рассуждений видно, что каждая вершина из этой компоненты становится активной точно один раз. Внутренний цикл for для активной вершины  выполняется
выполняется  раз. Следовательно, общее число повторений внутреннего цикла будет равно
раз. Следовательно, общее число повторений внутреннего цикла будет равно  .
.
Итак, процедура BFS( 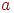 ) производит обход компоненты связности, содержащей вершину
) производит обход компоненты связности, содержащей вершину 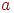 . Чтобы перейти к другой компоненте, достаточно выбрать какую-нибудь новую вершину (если такие вершины еще имеются), в качестве стартовой. Пусть
. Чтобы перейти к другой компоненте, достаточно выбрать какую-нибудь новую вершину (если такие вершины еще имеются), в качестве стартовой. Пусть  - множество вершин графа. Следующий алгоритм осуществляет полный обход графа методом поиска в ширину.
- множество вершин графа. Следующий алгоритм осуществляет полный обход графа методом поиска в ширину.
Алгоритм 1.Поиск в ширину.
1.пометить все вершины как новые
2.создать пустую очередь 
3.for  do if
do if 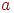 новая then BFS(
новая then BFS( 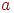 )
)
Учитывая, что цикл for в строке  повторяется
повторяется  раз, где
раз, где  - число вершин графа, получаем общую оценку трудоемкости
- число вершин графа, получаем общую оценку трудоемкости  . Необходимо отметить, что эта оценка справедлива в предположении, что время, требуемое для просмотра окрестности вершины, пропорционально степени этой вершины. Это имеет место, например, если граф задан списками смежности. Если же граф задан матрицей смежности, то для просмотра окрестности любой вершины будет затрачиваться время, пропорциональное
. Необходимо отметить, что эта оценка справедлива в предположении, что время, требуемое для просмотра окрестности вершины, пропорционально степени этой вершины. Это имеет место, например, если граф задан списками смежности. Если же граф задан матрицей смежности, то для просмотра окрестности любой вершины будет затрачиваться время, пропорциональное  . В этом случае общее время работы алгоритма будет оцениваться как
. В этом случае общее время работы алгоритма будет оцениваться как  . Наибольшее значение величины
. Наибольшее значение величины  при данном
при данном  равно
равно  , т.е. имеет порядок
, т.е. имеет порядок 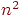 . Таким образом, трудоемкость алгоритма поиска в ширину при задании графа списками смежности не выше, чем при задании матрицей смежности. В целом же первый способ задания предпочтительнее, так как дает выигрыш для графов с небольшим числом ребер.
. Таким образом, трудоемкость алгоритма поиска в ширину при задании графа списками смежности не выше, чем при задании матрицей смежности. В целом же первый способ задания предпочтительнее, так как дает выигрыш для графов с небольшим числом ребер.
В качестве простейшего примера применения поиска в ширину для графа рассмотрим задачу выявления компонент связности. Допустим, мы хотим получить ответ в виде таблицы, в которой для каждой вершины  указан номер
указан номер  компоненты, которой принадлежит эта вершина. Компоненты будут получать номера в процессе обхода. Для решения этой задачи достаточно ввести переменную
компоненты, которой принадлежит эта вершина. Компоненты будут получать номера в процессе обхода. Для решения этой задачи достаточно ввести переменную  со значением, равным текущему номеру компоненты, и каждый раз при посещении новой вершины
со значением, равным текущему номеру компоненты, и каждый раз при посещении новой вершины  полагать
полагать 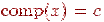 . Значение
. Значение  первоначально устанавливается равным
первоначально устанавливается равным  и модифицируется при каждом вызове процедуры BFS.
и модифицируется при каждом вызове процедуры BFS.
Процедура поиска в глубину
Поиск в глубину - вероятно, наиболее важная ввиду многочисленности приложений стратегия обхода графа. Идея этого метода - идти вперед в неисследованную область, пока это возможно, если же вокруг все исследовано, отступить на шаг назад и искать новые возможности для продвижения вперед. Метод поиска в глубину известен под разными названиями, например, "бэктрекинг", "поиск с возвращением".
Понятия новой, открытой, закрытой и активной вершин для поиска в глубину имеют такой же смысл, как и для поиска в ширину. Отметим, что всегда имеется не более чем одна активная вершина.
Обход начинается с посещения заданной стартовой вершины 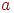 , которая становится активной и единственной открытой вершиной. Затем выбирается инцидентное вершине
, которая становится активной и единственной открытой вершиной. Затем выбирается инцидентное вершине 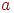 ребро
ребро 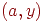 и посещается вершина
и посещается вершина 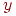 . Она становится открытой и активной. Заметим, что при поиске в ширину вершина
. Она становится открытой и активной. Заметим, что при поиске в ширину вершина 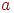 оставалась активной до тех пор, пока не были исследованы все инцидентные ей ребра. В дальнейшем, как и при поиске в ширину, каждый очередной шаг начинается с выбора активной вершины из множества открытых вершин. Если все ребра, инцидентные активной вершине
оставалась активной до тех пор, пока не были исследованы все инцидентные ей ребра. В дальнейшем, как и при поиске в ширину, каждый очередной шаг начинается с выбора активной вершины из множества открытых вершин. Если все ребра, инцидентные активной вершине  , уже исследованы, она превращается в закрытую. В противном случае выбирается одно из неисследованных ребер
, уже исследованы, она превращается в закрытую. В противном случае выбирается одно из неисследованных ребер  , это ребро исследуется. Если вершина
, это ребро исследуется. Если вершина 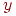 новая, то она посещается и превращается в открытую.
новая, то она посещается и превращается в открытую.
Главное отличие от поиска в ширину состоит в том, что при поиске в глубину в качестве активной выбирается та из открытых вершин, которая была посещена последней. Для реализации такого правила выбора наиболее удобной структурой хранения множества открытых вершин является стек: открываемые вершины складываются в стек в том порядке, в каком они открываются, а в качестве активной выбирается последняя вершина. Схематически это показано на рис. 2.

Рис. 2.
Обозначим стек для открытых вершин через  , остальные обозначения сохраняют тот же смысл, что и в предыдущем разделе. Через
, остальные обозначения сохраняют тот же смысл, что и в предыдущем разделе. Через  обозначается верхний элемент стека (т.е. последний элемент, добавленный к стеку). Тогда процедура обхода одной компоненты связности методом поиска в глубину со стартовой вершиной
обозначается верхний элемент стека (т.е. последний элемент, добавленный к стеку). Тогда процедура обхода одной компоненты связности методом поиска в глубину со стартовой вершиной 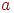 может быть записана следующим образом (DFS - Depth First Search).
может быть записана следующим образом (DFS - Depth First Search).
Procedure DFS(a)
1.посетить вершину 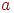
2. 
3.while 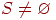 do
do
4. 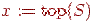
5.if имеется неисследованное ребро 
6.then исследовать ребро 
7.if вершина 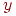 новая
новая
8.then посетить вершину 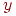
9. 
10. else удалить  из
из 
Еще раз обратим внимание на основное отличие этой процедуры от аналогичной процедуры поиска в ширину. При поиске в ширину вершина, став активной, остается ею, пока не будет полностью исследована ее окрестность, после чего она становится закрытой. При поиске в глубину, если в окрестности активной вершины  обнаруживается новая вершина
обнаруживается новая вершина 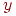 , то
, то 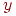 помещается в стек и при следующем повторении цикла while станет активной. При этом
помещается в стек и при следующем повторении цикла while станет активной. При этом  остается в стеке и через какое-то время снова станет активной. Иначе говоря, ребра, инцидентные вершине
остается в стеке и через какое-то время снова станет активной. Иначе говоря, ребра, инцидентные вершине  , будут исследованы не подряд, а с перерывами.
, будут исследованы не подряд, а с перерывами.
Алгоритм обхода всего графа - тот же, что и в случае поиска в ширину, только нужно очередь заменить стеком, а процедуру BFS - процедурой DFS.
Свойства 1 и 2 поиска в ширину, отмеченные в предыдущем разделе, сохраняются и для поиска в глубину. Остается верной и оценка трудоемкости  , но ее доказательство требует несколько иных рассуждений, так как каждая вершина теперь может становиться активной несколько раз. Однако каждое ребро рассматривается только два раза (один раз для каждой инцидентной ему вершины), поэтому в операторе if в строке 5 ветвь then (строки 6-9) повторяется
, но ее доказательство требует несколько иных рассуждений, так как каждая вершина теперь может становиться активной несколько раз. Однако каждое ребро рассматривается только два раза (один раз для каждой инцидентной ему вершины), поэтому в операторе if в строке 5 ветвь then (строки 6-9) повторяется 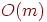 раз. В этом же операторе ветвь else (строка 10) повторяется
раз. В этом же операторе ветвь else (строка 10) повторяется  раз, так как каждая вершина может быть удалена из стека только один раз. В целом получается
раз, так как каждая вершина может быть удалена из стека только один раз. В целом получается  .
.
Дата добавления: 2018-05-02; просмотров: 576; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
