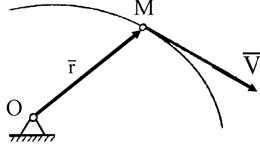
Кинематика плоскопараллельного движения твердого тела

КИНЕМАТИКА

Кинематика точки

Определить движение точки - это значит уметь определить положение точки по отношению к выбранной системе отсчета в любой момент времени.

В кинематике применяются три способа задания движения точки: векторный, координатный и естественный.

При векторном способе определения движения точки радиус-вектор движущейся точки М (рис. 21), проведенный из выбранного неподвижного центра О, выражается как векторная функция от времени, т. е.

Рис. 21

Скорость точки, характеризующая быстроту и направление движения точки, равна производной по времени от ее радиуса-вектора:

Ускорение точки, характеризующее изменение скорости по модулю и направлению, равно производной по времени от вектора скорости:

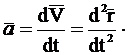
Координатный способ определения (задания) движения точки состоит в том, что координаты движущейся точки в выбранной системе координат выражаются как функции времени t.

Уравнения движения точки в декартовых координатах имеют вид

x = x(t), y = y (t), z = z (t).

Если точка движется в плоскости Оху, то будем иметь только два уравнения движения:

x = x(t), y = y (t).

Для того чтобы найти траекторию точки, достаточно из уравнений движения исключить время t. Вектор скорости и вектор ускорения определяются по их проекциям на оси декартовых координат, причем

Отсюда получаем формулы разложения векторов скорости и ускорения по координатным осям:

Модули векторов скорости и ускорения вычисляем по формулам

При естественном способе движение точки задается ее траекторией и уравнением движения по этой траектории:

где О - начало отсчета дуг на траектории; s - дуговая координата точки М или взятая с соответствующим знаком длина дуги, отсчитываемая вдоль траектории от начала отсчета до точки М (рис. 22).

Рис. 22

Если заданы траектория движущейся точки и закон ее движения по этой траектории s = s (t), то вектор скорости направлен по касательной к этой траектории, а его проекция на направление касательной определяется по формуле

причем абсолютное значение этой проекции равно модулю скорости:

Вектор ускорения определяется по его проекциям на естественные оси (касательную, главную нормаль и бинормаль):

где r - радиус кривизны траектории в данной точке.

Следовательно,

Отметим частные случаи:

1. Если точка движется прямолинейно и неравномерно, то радиус кривизны траектории r ® µ и, следовательно, а_n = 0. В этом случае ускорение направлено вдоль траектории точки и по модулю равно

2. Если точка движется по криволинейной траектории равномерно, то

V = const и

и поэтому ускорение направлено по нормали к траектории и по модулю равно

3. Если точка движется прямолинейно и равномерно, то a_n = 0, a_t = 0 и a = 0.

В том случае, когда движение точки задано в координатной форме, касательное ускорение определяется по формуле

, или

После этого нормальное ускорение можно найти из равенства

где

Определив , найдем радиус кривизны по формуле

Если плоская траектория задана уравнением у = у(х), то радиус кривизны траектории вычисляется по формуле

где и

Пример K1. Даны уравнения движения точки в плоскости ху:

x = 6×cos (p×t/6) – 3, y = – 4×cos² (p×t/6)

(х, у - в метрах, t - в секундах).

Определить уравнение траектории точки. Для момента времени t₁ = 1 с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Решение. Для определения траектории исключим из заданных уравнений движения время t, воспользовавшись подстановкой:

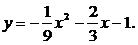
Из полученного выражения следует, что траекторией движения точки является парабола с нисходящими ветвями и осью, параллельной оси у; вершина параболы находится в точке с координатами х = -3 м, у = 0.

Найдем проекции вектора скорости на оси координат:

Подставив t₁ = 1 с в полученные выражения, находим

Скорость точки в момент времени t₁ = 1 с

Найдем проекции вектора ускорения:

Для момента времени t₁ = 1 с

м/с².

Касательное ускорение найдем по формуле

м/с².

Нормальное ускорение

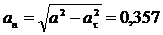м/с².

Вычислим радиус кривизны траектории в том месте, где находится точка в момент времени t₁ = 1 с:

м.

Рис. K1

Пользуясь уравнением траектории, вычерчиваем параболу (рис. K1) и показываем на ней точку М в заданный момент времени по ее координатам. Вектор скорости строим по составляющим и ; он должен быть направлен по касательной к траектории. Вектор ускорения находим по его составляющим и . Далее найденный вектор раскладываем на направления касательной и нормали и получаем векторы касательного и нормального ускорений. Полученные таким образом значения и должны совпасть с результатами их подсчета по формулам.

Кинематика плоскопараллельного движения твердого тела

Плоскопараллельным (плоским) движением твердого тела называется такое движение, при котором траектории всех его точек лежат в плоскостях, параллельных некоторой неподвижной плоскости. Пусть тело движется параллельно некоторой неподвижной плоскости П (рис. 23). Если пересечь данное тело плоскостью хОу, параллельной неподвижной плоскости П, то в сечении получится какая-то плоская фигура S. Эта фигура будет перемещаться при движении тела, оставаясь все время в той же плоскости хОу. Очевидно, что при таком движении тела все его точки, лежащие на перпендикуляре Аа к плоскости фигуры, движутся совершенно одинаково, так же как и точка А этой фигуры. Все точки, расположенные на перпендикуляре Вв к плоскости фигуры , движутся так же, как и точка В этой фигуры, и т. д. Отсюда следует, что для определения плоского движения тела достаточно знать движение плоской фигуры в ее плоскости.

Положение неизменяемой плоской фигуры S в ее плоскости вполне определяется положением двух произвольных ее точек А и В. Следовательно, изучение движения плоской фигуры в ее плоскости сводится к изучению движения прямолинейного отрезка АВ, с которым фигура неизменно связана. Но положение отрезка АВ определяется двумя координатами х_А и у_А точки А, называемой полюсом и углом j, который образует этот отрезок с некоторой осью неизменного направления, лежащей в плоскости данной фигуры (рис. 24).

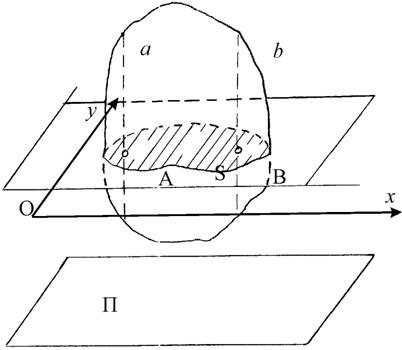
Рис. 23

Рис. 24

Таким образом, движение плоской фигуры в ее плоскости можно определить следующими тремя уравнениями:

x_A = х_A (t),

y_A = y_A (t),

j = j (t).

Из этих уравнений следует, что движение плоской фигуры можно разложить на два движения: 1) поступательное движение вместе с полюсом А и определяемое первыми двумя уравнениями и 2) вращательное движение вокруг полюса, определяемое третьим уравнением. При этом угловая скорость вращательного движения не зависит от выбора полюса. Очевидно, что скорость любой точки В плоской фигуры равна геометрической сумме двух скоростей: скорости полюса и скорости точки В во вращательном движении вокруг полюса (рис. 25), т. е.

= + ,

причем ^ АВ и = w×АВ.

Отсюда следует теорема о проекциях скоростей точек плоской фигуры: проекции скоростей двух точек плоской фигуры на ось h, проходящую через эти точки, равны между собой.

Мгновенным центром скоростей (МЦС) называется такая точка Р плоской фигуры, скорость которой в данный момент равна нулю.

Если известны скорость какой-либо точки А плоской фигуры и угловая скорость w этой фигуры, то, повернув вектор вокруг точки А на 90° в направлении вращения фигуры и отложив на этой полупрямой отрезок

АР = /w,

получим точку Р, которая является МЦС (рис. 25).

Рис. 25

Если же известны направления скоростей двух точек плоской фигуры, то МЦС находят как точку пересечения перпендикуляров, восстановленных в этих точках к направлениям их скоростей.

Если мгновенный центр скоростей Р найден и если известна угловая скорость фигуры, то скорость любой точки В фигуры определяется как скорость этой точки во вращательном движении вокруг МЦС, т. е. вектор перпендикулярен к отрезку РВ и по модулю равен w×РВ. Отсюда следует, что скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей, т. е.

Отметим другие случаи нахождения положения МЦС.

Если скорости точек А и В параллельны и АВ ^ , то для определения положения МЦС следует воспользоваться свойством пропорциональности скоростей расстояниям точек до мгновенного центра скоростей. На рис. 26, а, б представлено, как находится МЦС в этих случаях.

На рис. 26, в показан случай, когда и параллельны, но неперпендикулярна отрезку АВ. Очевидно, что в этом случае прямые Аа и Вв, перпендикулярные и , пересекаются в бесконечности и мгновенного центра скоростей не существует, а угловая скорость фигуры равна нулю (w = 0). На основании теоремы о проекциях скоростей имеем V_A×cos a = V_B×cos a, отсюда V_A = V_B и = . Значит, в данный момент времени скорости всех точек плоской фигуры равны по модулю и направлению.

Рис. 26

При качении без скольжения одного тела по поверхности неподвижного другого (рис. 26, г) МЦС совпадает с точкой Р соприкосновения тел (так как при отсутствии скольжения скорость точки соприкосновения равна нулю).

Ускорение любой точки движущейся плоской фигуры можно определить как геометрическую сумму ускорений этой точки в поступательном движении вместе с некоторым полюсом и вращательным движением вокруг этого полюса.

Если известны ускорение некоторой точки А фигуры (ускорение полюса), а также угловая скорость w и угловое ускорение e фигуры, то ускорение любой ее точки В определяется по формуле

= + = + + .

Здесь вектор - ускорение точки В во вращательном движении вокруг полюса А; и - нормальная и касательная составляющие этого вектора, которые вычисляем по формулам:

= w²× АВ, = e × АВ.

При этом вектор направлен вдоль ВА (от точки В к точке А), а вектор перпендикулярен к ВА (рис. 27).

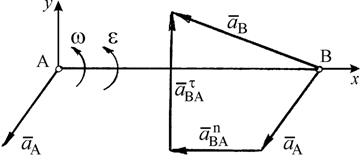
Рис. 27

Ускорение точки В можно определить, если спроецировать векторное равенство

= + +

на оси х и у (см. рис. 27) и найти проекции этого ускорения:

= – , = + .

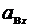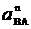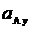По проекциям находят модуль ускорения точки В:

Указания. Задача К2 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звенумеханизма в отдельности.

При определении ускорений точек механизма исходить из векторного равенства 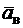= + + , где А – точка, ускорение которой или задано, или непосредственно определяется по условиям задачи (если точка А движется по дуге окружности, то = + 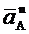); В – точка, ускорение 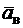которой нужно определить (о случае, когда точка В тоже движется по дуге окружности, см. примечание в конце рассмотренного ниже примера К2).

Пример К2. Механизм (рис. К2а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами O₁ и О₂ шарнирами.

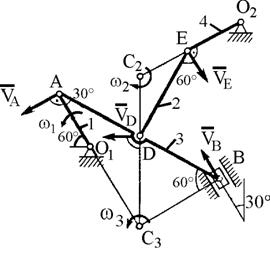
Рис. К2а Рис. К2б

Дано: a = 60°, b = 150°, g = 90°, j = 30°, q = 30°, AD = DB, l₁ = 0,4 м, l₂= 1,2 м, l₃ = 1,4 м, w₁ = 2 c^–1, e₁ = 7 с^–2 (направления w₁ и e₁ – против хода часовой стрелки). Определить: V_B, V_E, w₂, a_B, e₃.

Решение.1. Строим положение механизма в соответствии с заданными углами (рис. К2б; на этом рисунке изображаем все векторы скоростей).

2. Определяем V_B. Точка В принадлежит стержню АВ. Чтобы найти V_B, надо знать скорость какой-нибудь другой точки этого стержня и направление 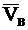. По данным задачи, учитывая направление w₁, можем определить ; численно

V_A = w₁×l₁ = 0,8 м/с; ^ О₁А. (45)

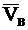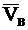Направление найдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная и направление , используем теорему о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 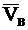(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим:

V_В× cos 30° = V_A × cos 60° и V_В = 0,46 м/с. (46)

3. Рассчитываем . Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить , надо сначала найти скорость точки D, принадлежащей одновременно стержню АВ. Для этого, зная и 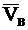, строим мгновенный центр скоростей (МЦС) стержня АВ; это точка С₃, лежащая на пересечении перпендикуляров к и 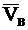, восставленных из точек А и В (к перпендикулярен стержень 1). По направлению вектора определяем направление поворота стержня АВ вокруг МЦС С₃. Вектор перпендикулярен к отрезку С₃D, соединяющему точки D и С₃, и направлен в сторону поворота. Величину V_D найдем из пропорции

(47)

Чтобы вычислить С₃D и С₃B, заметим, что DAС₃В – прямоугольный, так как острые углы в нем равны 30° и 60°, и что С₃В = AB × sin 30° = 0,5 × AB = ВD. Тогда DВС₃D является равносторонним и С₃B = С₃D. В результате равенство (47) дает:

V_D = V_B = 0,46 м/с; ^ C₃D. (48)

Так как точка Е принадлежит одновременно стержню O₂E, вращающемуся вокруг O₂, то ^ O₂E, тогда, проведя из точек Е и Dперпендикуляры к скоростям и , построим МЦС С₂ стержня DE. По направлению вектора определяем направление поворота стержня DE вокруг центра С₂. Вектор направлен в сторону поворота этого стержня. Из рис. К2б видно, что ÐC₂ED = ÐC₂DE = 30°, откуда C₂E = C₂D. Составив теперь пропорцию, найдем, что

V_E = V_D = 0,46 м/с. (49)

4. Определяем w₂. Так как МЦС стержня 2 известен (точка С₂) и С₂D = l₂/(2 × cos 30°) = 0,69 м, то

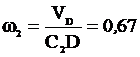c^–1. (50)

5. Определяем (рис. К2в, на котором изображены все векторы ускорений). Точка В принадлежит стержню АВ. Чтобы найти , надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию точки В. По данным задачи можем определить = + 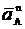, где численно

= e₁× l₁ = 2,8 м/с²;

(51)

= × l₁ = 1,6 м/с².

Рис. К2в

Вектор 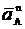направлен вдоль AO₁, а – перпендикулярно к AO₁; изображаем эти векторы на чертеже (см. рис. К2в). Так как точка В одновременно принадлежит ползуну, то вектор 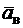параллелен направляющим ползуна. Изображаем вектор 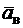на чертеже, полагая, что он направлен в ту же сторону, что и .

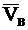Для определения 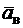воспользуемся равенством

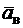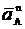= + + + . (52)

Изображаем на чертеже векторы (вдоль ВА от В к А) и (в любую сторону перпендикулярно к ВА); численно = w₃²× l₃. Находим w₃ с помощью МЦС C₃ стержня 3:

c^–1 и = 0,61 м/с². (53)

Таким образом, у величин, входящих в равенство (52), неизвестны только числовые значения а_В и ; их можно найти, спроектировав обе части равенства (52) на какие-нибудь две взаимно перпендикулярные оси.

Чтобы определить а_В, спроектируем обе части равенства (52) на направление ВА (ось х), перпендикулярное к неизвестному вектору . Тогда получим:

а_В× сos 30° = × cos 60° – × cos 30° + . (54)

Подставив в равенство (54) числовые значения всех величин из (51) и (53), найдем, что

а_В = 0,72 м/с². (55)

Так как получилось а_В > 0, то, следовательно, вектор направлен как показано на рис. К2в.

6. Находим e₃. Чтобы найти e₃, сначала вычислим . Для этого обе части равенства (52) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим:

– а_В× sin 30° = × sin 60° + × sin 30° + . (56)

Подставив в равенство (56) числовые значения всех величин из (55) и (51), найдем, что = – 3,58 м/с². Знак указывает, что направление противоположно показанному на рис. К2в. Теперь из равенства = e₃× l₃ получим:

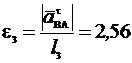c^–2.

Ответ: V_B = 0,46 м/с; V_E = 0,46 м/с;

w₂ = 0,67 с¹; а_B = 0,72 м/с²; e₃ = 2,56 с^–2.

Примечание 1. Если точка B, ускорение которой определяется, движется не прямолинейно (например, как на рис. К2.0–К2.4, где В движется по окружности радиуса О₂В), то направление заранее неизвестно.

В этом случае также следует представить двумя составляющими ( = + ) и исходное уравнение (52) примет вид

+ = + + + . (57)

При этом вектор (см., например, рис. К2.0) будет направлен вдоль BO₂, а вектор – перпендикулярно ВО₂ в любую сторону. Числовые значения , и определяются так же, как в рассмотренном примере (в частности, по условиям задачи может быть = 0 или = 0, если точка А движется прямолинейно).

Значение вычисляется по формуле = /r = /l, где l – радиус окружности О₂В, а определяется так же, как скорость любой другой точки механизма.

После этого в равенстве (57) остаются неизвестными только значения и и они, как и в рассмотренном примере, находятся проецированием обеих частей равенства (57) на две взаимно-перпендикулярные оси.

Найдя , можем вычислить искомое ускорение 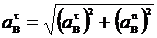. Величина служит для нахождения e_АВ (как в рассмотренном примере).

Примечание 2. Если требуется определить ускорение точки D звена АВ (рис. К2г), то следует воспользоваться векторным равенством:

= + + + .

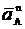Рис. К2г

Ускорение точки D найдем по его проекциям на координатные оси, спроецировав приведенное выше векторное равенство на эти оси:

= × cos 60° – × cos 30° + ,

= × sin 60° + × sin 30° + .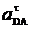

Здесь = w₃²×AD, 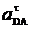= e₃×AD.

Вектор направлен от точки D к точке А, а вектор перпендикулярен к DА.

Дата добавления: 2018-05-02; просмотров: 631; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!