С)Бесконечность определенного количества 8 страница
Другую главную область, к которой прилагается диференциальное исчисление, представляет механика; попутно мы отчасти уже касались смысла различных степенных функций, получающихся при элементарных уравнениях ее предмета, движения; здесь я буду говорить о них непосредственно. Уравнение, а именно математическое выражение просто равномерного движения 
или 
, в котором пройденные пространства пропорциональны протекшим временам по некоторой эмпирической единице c, величине скорости, не имеет смысла диференцировать; коэфициент с уже совершенно определен и известен, и здесь не может иметь места никакое дальнейшее развертывание степени, никакое дальнейшее разложение в ряд. — Как анализируется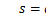 
, уравнение движения падения тел, об этом мы уже вкратце сказали выше; первый член анализа 
выражается словесно и, следовательно, понимается, как существующий реально таким образом, что он есть член некоторой суммы (каковое представление мы уже давно устранили), одна часть движения и притом та часть его, которая приписывается силе инерции, т. е., просто-равномерной скорости таким образом, что в бесконечно-малых частях времени движение принимается за равномерное, а в конечных частях времени, т. е. в существующих на самом деле, — за неравномерное. Разумеется, 
и значение a и t, взятых сами по себе, известно, равно как известно и то, что этим самым дано определение скорости равномерного движения: так как 
, то вообще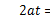 
; но этим мы нисколько не подвинулись вперед в нашем знании; лишь ложное предположение, будто 
есть часть движения как некоторой суммы, дает ложную видимость физического предложения. Самый множитель, a, эмпирическая единица — некоторое определенное количество, как таковое — приписывается тяготению; если здесь применяют категорию силы тяготения, то нужно сказать, что, наоборот, как раз целое 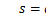есть действие или, лучше сказать, закон тяготения. — То же самое верно и относительно выведенного из положения, гласящего, что если бы прекратилось действие силы тяжести, то тело со скоростью, приобретенной им в конце своего падения, прошло бы во время, равное времени его падения, пространство вдвое большее пройденного. — В этом положении заключается также и сама по себе превратная метафизика: конец падения или конец той части времени, в которое падало тело, всегда сам еще есть некоторая часть времени; если бы он не был таковой частью, то наступил бы покой и, следовательно, не было бы никакой скорости; скорость может быть установлена лишь по пространству, пройденному в некоторую часть времени, а не в конце ее. Если же кроме того и в других физических областях, где вовсе нет никакого движения, как например относительно поведения света (помимо того, что называют его распространением в пространстве) и относительно определений величин в цветах, применяют диференциальное исчисление и первая производная функция некоторой квадратной функции здесь также именуется скоростью, то на это следует смотреть, как на еще более несостоятельный формализм выдумывания существования. —
|
|
|
|
|
|
Движение, изображаемое уравнением 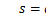, говорит Лагранж, мы находим в опыте падения тел; простейшим следующим за ним было бы движение, уравнением которого является 
, но такого движения не оказывается в природе; мы не знали бы, что может означать собою коэфициент c. Если это верно, то, напротив, существует движение, уравнением которого является 
— кеплеровский закон движения тел солнечной системы. И разрешение вопроса о том, что здесь должна означать первая производная функция 
и т. д., а также дальнейшая непосредственная разработка этого уравнения путем диференцирования, развитие законов и определений указанного абсолютного движения, отправляясь от этой исходной точки зрения, должно бы, конечно, представить собою интересную задачу, в решении которой анализ явил бы себя в достойнейшем блеске.
|
|
|
Таким образом само по себе взятое приложение диференциального исчисления к элементарным уравнениям движения не представляет реального интереса; формальный же интерес проистекает из общего механизма исчисления. Но иное значение получает разложение движения в отношении определения его траектории; если последняя есть кривая и ее уравнение содержит высшие степени, то требуются переходы от прямолинейных функций возвышения в степень к самим степеням, а так как первые должны быть выведены из первоначального уравнения движения, содержащего фактор времени, с элиминированием времени, то этот фактор вместе с тем должен быть низведен к тем низшим функциям развертывания, из которых могут быть получены означенные уравнения линейных определений. Эта сторона приводит к рассмотрению интереса другой части диференциального исчисления.
Сказанное доселе имело своей целью выделить и установить простое специфическое определение диференциального исчисления и показать наличие этого определения на некоторых элементарных примерах. Это определение, как оказалось, состоит в том, что из уравнения степенных функций находят коэфициент члена разложения, так называемую первую производную функцию, и что обнаруживают наличие того отношения, которое она собою представляет, в моментах конкретного предмета, посредством какового, полученного таким образом уравнения между обоими отношениями определяются сами эти моменты. Мы должны вкратце рассмотреть также и принцип интегрального исчисления и установить, что получается из его приложения для его специфического конкретного определения. Понимание этого исчисления было нами упрощено и определено более правильно уже благодаря одному тому, что мы его больше не принимаем за метод суммирования, как его назвали в противоположность диференцированию (в котором приращение считается существенным ингредиентом), вследствие чего интегрирование представлялось находящимся в существенной связи с формой ряда. — Что касается задачи этого исчисления, то таковой, во-первых, так же как и в диференциальном исчислении, является теоретическая или, скорее, формальная задача, но, как известно, обратная задаче диференцирования. Здесь исходят из функции, рассматриваемой как производная, как коэфициент ближайшего члена, получающегося в результате разложения в ряд некоторого, пока еще неизвестного уравнения, а из этой производной должна быть найдена первоначальная степенная функция; та функция, которая в естественном порядке развертывания должна быть рассматриваема как первоначальная, здесь выводится, а рассматривавшаяся ранее как производная есть здесь данная или вообще начальная. Но формальная сторона этого действия представляется уже выполненной диференциальным исчислением, так как в последнем устанавливается вообще переход и отношение первоначальной функции к функции, получающейся в результате разложения в ряд. Если при этом отчасти уже для того, чтобы взяться за ту функцию, из которой следует исходить, отчасти же для того, чтобы осуществить переход от нее к первоначальной функции, оказывается необходимым во многих случаях прибегнуть к форме ряда, то следует прежде всего твердо помнить, что эта форма как таковая не имеет непосредственно ничего общего с собственным принципом интегрирования.
|
|
|
Но другой стороной задачи этого исчисления является с точки зрения формальной операции его приложение. А последнее само представляет собой задачу узнать, какое предметное значение (в вышеуказанном смысле) имеет та первоначальная функция, которую мы находим по данной функции, принимаемой за первую [производную]. Может казаться, что с этим учением, взятым само по себе, также покончено уже в диференциальном исчислении. Однако здесь появляется дальнейшее обстоятельство, вследствие которого дело оказывается не так просто. А именно, так как в этом исчислении оказывается, что благодаря первой производной функции уравнения кривой получилось некоторое линейное отношение, то тем самым мы также знаем, что интегрирование этого отношения дает уравнение кривой в виде отношения абсциссы и ординаты; или, если бы было дано уравнение для площади кривой, то диференциальное исчисление должно было бы предварительно научить нас относительно значения первой производной функции такого уравнения, что эта функция представляет ординату как функцию абсциссы, стало быть, представляет уравнение кривой.
Но главное дело здесь в том, какой из моментов определения предмета дан в самом уравнении, ибо лишь от данного может отправляться аналитическая трактовка, чтобы переходить от него к прочим определениям предмета. Дано, например, не уравнение поверхности, образуемой кривою, и не уравнение возникающего посредством ее вращения тела, а также и не уравнение некоторой дуги этой кривой, а лишь отношение абсциссы и ординаты в уравнении самой кривой. Переходы от указанных определений к самому этому уравнению не могут уже поэтому быть предметом самого диференциального исчисления; нахождение таких отношений есть дело интегрального исчисления.
Но, далее, было уже показано, что диференцирование уравнения с несколькими переменными величинами дает степенной член разложения (die Entwicklungspotenz) (53) или диференциальный коэфициент не как уравнение, а только как отношение; задача состоит затем в том, чтобы в моментах предмета указать для этого отношения, которое есть производная функция, другое равное ему. Напротив, предметом интегрального исчисления является само отношение первоначальной к производной, в этом случае данной функции, и задача состоит в том, чтобы указать значение искомой первоначальной функции в предмете данной первой производной функции или, вернее, так как это значение, например, площадь, ограничиваемая кривой или подлежащая ректифицированию, представляемая в виде прямой кривая и т. д., уже высказано как задача, то требуется показать, что такое определение может быть найдено посредством некоторой первоначальной функции, и вместе с тем показать, каков тот момент предмета, который для этой цели должен быть принят за исходную функцию, каковою в данном случае служит производная функция.
Обычный метод, пользующийся представлением бесконечно малой разности, слишком облегчает себе задачу. Для квадратуры кривых линий он принимает бесконечно малый треугольник, произведение ординаты на элемент (т. е. на бесконечно малую часть) абсциссы, за трапецию, имеющую одной своей стороной бесконечно-малую дугу, противоположную сказанной бесконечно-малой части абсциссы. Произведение это и интегрируется в том смысле, что интеграл дает сумму бесконечно многих трапеций, ту плоскость, которую требуется определить, т. е.конечную величину сказанного элемента плоскости. И точно так же обычный метод образует из бесконечно-малой дуги и соответствующих ей ординаты и абсциссы прямоугольный треугольник, в котором квадрат этой дуги считается равным сумме квадратов обоих других бесконечно малых, интегрирование которых и дает конечную дугу.
Этот прием имеет своей предпосылкой то общее открытие, которое лежит в основании этой области анализа и которое здесь выступает в виде положения о том, что квадратура кривой, выпрямленная дуга и т. д. находится к известной (данной уравнением кривой) функции в отношении так называемой первоначальной функции к производной. Здесь дело идет о том, чтобы в случае, если известная часть какого-нибудь математического предмета (например, некоторой кривой) принимается за производную функцию, узнать, какая другая его часть выражается соответствующей первоначальной функцией. Мы знаем, что если данная уравнением кривой функция ординаты принимается за производную функцию, то соответствующая ей первоначальная функция есть выражение величины отрезанной этой ординатой и кривой плоскости, что если как производная функция рассматривается известное определение касательной, то ее первоначальная функция выражает величину соответствующей этому определению дугии т. д. Однако заботу о том, чтобы узнать и доказать, что эти отношения — отношение первоначальной функции к производной в отношение величин двух частей или двух обстоятельств математического предмета — образуют пропорцию, — заботу об этом снимает с себя метод, пользующийся бесконечно-малым и механически оперирующий им. Своеобразной заслугой является уже то остроумие, с которым на основании результатов, известных уже заранее из других источников, этот метод открывает, что известные и именно такие-то стороны математического предмета находятся между собою в отношении первоначальной функции к производной.
Из этих двух функций производная или, как она была определена выше, функция возвышения в степень, есть здесь, в интегральном исчислении, данная по отношению к первоначальной функции, которая еще должна быть найдена из нее путем интегрирования. Однако первая дана не непосредственно, а равно не дано уже само по себе, какая часть или какое определение математического предмета должно быть рассматриваемо как производная функция, дабы через приведение этого определения к первоначальной функции найти другую часть или другое определение предмета, то определение, величину которого требуется установить. Обычный метод, сразу же представляющий, как мы сказали, известные части предмета как бесконечно-малые в форме производных функций, находимых из первоначально данного уравнения предмета вообще посредством диференцирования (как, например, для выпрямления кривой бесконечно-малые абсциссы и ординаты), принимает за таковые те части или определения, которые можно привести в такую связь с предметом задачи (в нашем примере с дугой), также представляемым, как бесконечно-малый, которая установлена элементарной математикой, благодаря чему, если известны означенные части, то определяется также и та часть, величину которой требуется найти; так, например, для выпрямления кривой указанные три бесконечно-малых приводятся в связь уравнения прямоугольного треугольника, для ее квадратуры ордината и бесконечно-малая абсцисса приводятся в связь некоторого произведения, причем площадь принимается вообще за арифметическое произведение линий. Переход от этих так называемых элементов площади, дуги и т. д. к величине самих площадей, дуги и т. д. считается тогда лишь восхождением от бесконечного выражения к конечному или к сумме бесконечно многих элементов, из которых, согласно предположению, состоит искомая величина.
Можно, поэтому, сказать лишь поверхностно, что интегральное исчисление есть только обратная, но вообще более трудная проблема диференциального исчисления. Дело обстоит, напротив, скорее так, что реальный интерес интегрального исчисления направлен исключительно на взаимное отношение первоначальной и производной функции в конкретных предметах.
Лагранж и в этой части исчисления столь же мало соглашался отделаться от трудности, которую представляли эти проблемы, рассмотренным гладким способом путем принятия вышеуказанных прямых допущений. Для разъяснения сущности дела будет полезно привести здесь также и некоторые детали его приема на немногих примерах. Этот прием ставит себе как раз задачей отдельно доказать, что между частными определениями некоторого математического целого, например некоторой кривой, имеет место отношение первоначальной функции к производной. Но в силу природы самого отношения, приводящего в связь в некотором математическом предмете кривые с прямыми линиями, линейные измерения и функции с поверхностно-плоскостными измерениями и их функцией и т. д., приводящего, следовательно, в связь качественно разное, это не может быть выполнено в указанной области прямым путем, и определение, таким образом, можно понимать лишь как середину между некоторым большим и некоторым меньшим. Благодаря этому, правда, само собою снова появляется форма приращения с плюсом и минусом, и бодрое «developpons» («развернем в ряд») снова очутилось на своем месте; но мы уже говорили выше о том, что здесь приращения имеют лишь арифметическое конечное значение. Из развертывания того условия, что подлежащая определению величина больше некоторого легко определяемого предела и меньше другого предела, выводится затем, например, что функция ординаты есть первая производная функция к функции площади.
Выпрямление прямых по способу, показанному Лагранжем, который при этом исходит из архимедовского принципа, интересно тем, что оно проливает свет на перевод архимедовского метода на язык принципа нового анализа, а это позволяет бросить взгляд во внутренний строй и в истинный смысл действия, механически производимого другим путем. Способ действия при этом по необходимости аналогичен вышеуказанному способу. Архимедовский принцип, согласно которому дуга кривой больше соответствующей ей хорды и меньше суммы двух касательных, проведенных в конечных точках дуги, поскольку эти касательные заключены между этими точками и точкой их пересечения, не дает прямого уравнения. Переводом этого архимедовского основного определения на язык новой аналитической формы служит изобретение такого выражения, которое, взятое само по себе, есть простое основное уравнение, между тем как указанная форма лишь выставляет требование двигаться, совершать переходы до бесконечности между некоторым слишком большим и некоторым слишком малым, которые каждый раз получают определенную величину, причем в результате такого постоянного движения всегда получаются опять-таки лишь новые слишком большие и слишком малые, но во все более и более тесных пределах. Посредством формализма бесконечно-малых сразу же создается уравнение 
. Исходя из указанной основы, лагранжево изложение доказывает, напротив, что величина дуги есть первоначальная функция к некоторой производной функции, характеризующий член которой сам есть функция отношения производной функции к первоначальной функции ординаты.
Так как в способе Архимеда, точно так же, как и позднее в исследовании Кеплером стереометрических предметов, встречается представление о бесконечно-малом, то это обстоятельство слишком часто приводилось в качестве авторитета в пользу того употребления, которое делают из этого представления в диференциальном исчислении, причем не выделялись черты своеобразия и отличия. Бесконечно-малое означает прежде всего отрицание определенного количества как такового, т. е. так называемого конечного выражения или той завершенной определенности, которой обладает определенное количество как таковое. И точно так же в последующих знаменитых методах Валериуса, Кавальери и др., основанных на рассмотрении отношений геометрических предметов, основным определением является положение о том, что определенное количество, как определенное количество таких определений, которые ближайшим образом рассматриваются лишь в отношении, оставляется для этой цели в стороне, и эти определения должны быть принимаемы сообразно с этим за не имеющие величины (Nicht-Grosses). Но отчасти этим не познано и не выделено то утвердительное вообще, которое лежит за исключительно отрицательным определением и которое выше оказалось, говоря абстрактно, качественной определенностью величины, состоящей, говоря более определенно, в степенном отношении; отчасти же, поскольку само это отношение в свою очередь включает в себя множество ближе определенных отношений, как например, отношение между некоторой степенью и функцией, получающейся в результате ее разложения в ряд, они должны были бы быть в свою очередь обоснованы всеобщим и отрицательным определением того же бесконечно-малого и выведены из него. В только что приведенном изложении Лагранжа найдено то определенное утвердительное, которое заключается в архимедовом способе развертывания задачи, и тем самым приему, обремененному неограниченным выхождением, дана его настоящая граница. Величие нового изобретения, взятого само по себе, и его способность разрешать до того времени неприступные задачи, а те задачи, которые и ранее были разрешимы, разрешать более простым способом, — это величие следует видеть исключительно в открытии отношения первоначальной функции к так называемой производной функции и тех частей математического целого, которые находятся в таком отношении.
Дата добавления: 2018-05-02; просмотров: 232; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!