Модуль 2.  Методы нахождения площади плоских фигур.

Содержание: 1. Модуль 1: Основные формулы площадей. 2. Модуль 2: Методы нахождения площадей. 3. Модуль 3: Задачи с решением. 4. Модуль 4: Задачи для закрепления. 5. Модуль 5: Задачи для самостоятельной работы и зачета.  

Модуль 1. Теоретическая часть

Основные определения и формулы для площадей фигур.

 Прямоугольник.

Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, т.е. составляют 90°.Площадь прямоугольника равна произведению его сторон .

Квадрат.

Квадратом называется параллелограмм с прямыми углами и равными сторонами. Квадрат есть частный вид прямоугольника, а также частный вид ромба. См. также площадь ромба. Площадь квадрата равна квадрату длины его стороны. Или половине квадрата диагонали.

;

Трапеция.

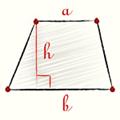Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. Площадь трапеции равна произведению полусуммы ее оснований на высоту.

 Площадь трапеции равна произведению её средней линии на высоту.

 

 

Параллелограмм.

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания на высоту.

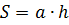
Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними.

Правильный многоугольник.

Для того чтобы вычислить площадь правильного многоугольника его разбивают на равные треугольники с общей вершиной в центре вписанной окружности. А площадь правильного многоугольника равна произведению его полупериметра на радиус вписанной окружности правильного многоугольника.

Выпуклый четырёхугольник.

 Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними.

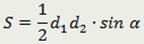
 Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон

Ромб.

Ромбом называется параллелограмм с равными сторонами. Квадрат есть частный вид ромба. У квадрата диагонали равны. См. также площадь квадрата. Площадь ромба равна половине произведения его диагоналей.

 Площадь ромба равна произведению квадрата его стороны на синус одного из его углов.

 

 

Сектор.

Сектор круга, окружности — это часть круга, окружности ограниченная дугой и двумя радиусами, проведенными к концам дуги. Площадь сектора круга равна произведению половины длины дуги сектора на радиус круга.

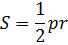
 Площадь кругового сектора равна произведению площади единичного сектора (сектор, соответствующий центральному углу с мерой равной единице) на меру центрального угла, соответствующего данному сектору ( формулы для случаев градусной и радианной мер центральных углов).

Окружность.

Окружность есть геометрическое место точек плоскости, равноудаленных от одной ее точки. Равные отрезки, соединяющие центр с точками окружности, называются радиусами. Круг есть часть плоскости, лежащая внутри окружности. Площадь круга равна произведению полуокружности на радиус.

Площадь сегмента круга, окружности.

Сегмент круга, окружности — это часть круга, окружности, ограниченная дугой и стягивающей ее хордой.

Площадь сегмента круга, окружности находится, как разность площади сектора и площади равнобедренного треугольника выраженную через угол.

Площадь кольца.

Площадь кольца через радиусы находится как произведение числаπ на разность квадратов внешнего и внутреннего радиусов кольца.

Площадь кольца через диаметры находится как произведение одной четвертой числа π на разность квадратов внешнего и внутреннего диаметров кольца.

 Площадь кругового кольца равна удвоенному произведению числа "пи", среднего радиуса кольца и его ширины.

Площадь сектора кольца.

Сектор кольца — это часть круга, окружности ограниченная дугами разных радиусов и двумя линиями радиусами, проведенными к концам дуги большего радиуса.

Площадь сектора кольца вычисляется как разность площадей большего и меньшего секторов круга.

Площадь сектора кольца если угол в градусах, вычисляется как произведение числа π на отношение угла сектора к углу полной окружности 360° и на разность квадратов большего и меньшего радиусов.

Площадь треугольника.

Треугольник образуется соединением отрезками трех точек, не лежащих на одной прямой. При этом точки называются вершинами треугольника, а отрезки - его сторонами. Площадь треугольника равна произведению половины основания треугольника на его высоту.

Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон.

Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.

 

Если один из углов прямой, то треугольник - прямоугольный. Площадь прямоугольного треугольника равна половине произведения катетов треугольника.

Площадь равнобедренного треугольника вычисляется по классической формуле площади треугольника — произведение половины основания треугольника на его высоту. Высоту мы подставим в эту формулу из формулы высоты равнобедренного треугольника.

 Площадь равностороннего треугольника вычисляется по классической формуле площади треугольника — произведение половины основания треугольника на его высоту. Высоту мы подставим в эту формулу из формулы высоты равностороннего треугольника

Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла.

Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов.

 Площадь треугольника равна произведению квадрата его полупериметра на тангенсы половин всех углов треугольника.

 

 Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности.

 

 Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов.

 

 Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник).

 

 

 Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника.

 

 

Шар и сфера.

 Шаровой, или сферической поверхностью (иногда просто сферой) называется геометрическое место точек пространства, равноудаленных от одной точки - центра шара. Площадь поверхности сферы равна учетверенной площади большого круга:

 

Куб.

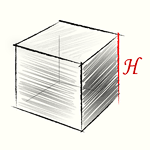Прямоугольный параллелепипед, все грани которого - квадраты, называется кубом. Все ребра куба равны, а площадь поверхности куба равна сумме площадей шести его граней, т.е.площади квадрата со стороной H умноженной на шесть. Площадь поверхности куба равна.

Конус.

Круглый конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называют также конусом вращения.

Боковая площадь поверхности круглого конуса равна произведению половины окружности основания на образующую.

Цилиндр.

Цилиндрической поверхностью называется поверхность, образуемая прямой, сохраняющей одно и тоже направление и пересекающей направляющую линию. Цилиндр — круговой если в основании его лежит круг. Площадь боковой поверхности круглого цилиндра равна произведению длины окружности основания на высоту.

Прямоугольный параллелепипед.

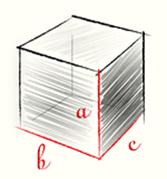Параллелепипедом называется призма, основание которой параллелограмм. Параллелепипед имеет шесть граней, и все они — параллелограммы. Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным. Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого параллелепипеда.

Усеченный конус.

Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом. Боковая площадь поверхности усеченного конуса вычисляется по формуле.

Шаровой сегмент.

Часть шара, осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом. Основанием шарового сегмента называется круг ABCD. Высотой шарового сегмента называется отрезок NM, т.е. длина перпендикуляра, восстановленного из центра N основания до пересечения с поверхностью шара. Точка M называется вершиной шарового сегмента. Площадь поверхности шарового сегмента равняется произведению его высоты на окружность большого круга шара.

Шаровой слой.

 Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями. Шаровой пояс или Шаровая зона — это кривая поверхность шарового слоя. Круги ABC и DEF это основания шарового пояса. Расстояние между основаниями это высота шарового слоя. Кривая поверхность шарового слоя равна произведению его высоты на окружность большого круга шара.

Шаровой сектор.

Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью основанием которой служит основание сегмента, а вершиной — центр шара. Поверхность шарового сектора складывается из кривых поверхностей шарового сегмента и конуса. Зная радиус основания сегмента и конуса r при помощи теоремы Пифагора и прямоугольного треугольника получим высоты сегмента и конуса:

 

 

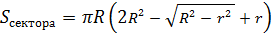
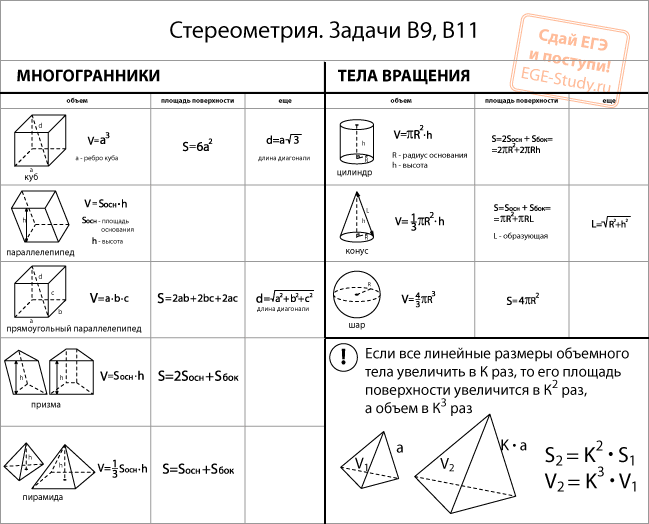
1.2.Справочные таблицы «Площади плоских фигур, площади поверхности и объема тел вращения»

Модуль 2.  Методы нахождения площади плоских фигур.

Рассмотрим несколько способов нахождения площади плоских фигур:

· формула Пика,

· метод обводки.

Формула Пика.

Формула, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём площадь треугольника:                Отметим узлы:

                 

1 клетка = 1 см

M = 15 (обозначены красным)

N = 34 (обозначены синим)

 

 

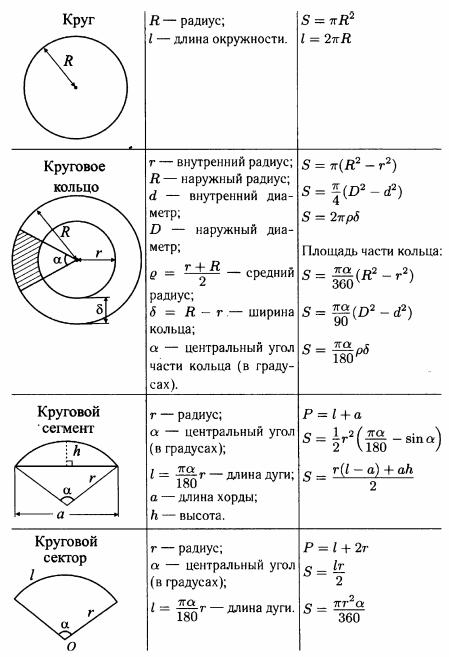
Пример 1. Найдём площадь параллелограмма:        Отметим узлы:

          

M = 18 (обозначены красным)

N = 20 (обозначены синим)

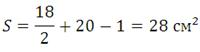
Пример 2. Найдём площадь трапеции:                      Отметим узлы:

                 

M = 24 (обозначены красным)

N = 25 (обозначены синим)

Пример 3. Найдём площадь многоугольника:                 Отметим узлы:

     

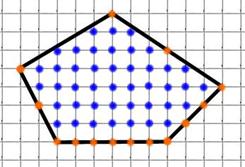
M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом. А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.

Теперь взгляните на следующие фигуры:

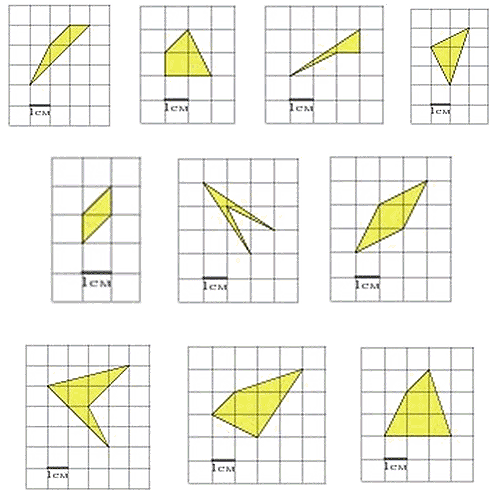
Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:

                          

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Ответ: 9,5

 

Метод обводки.

1. Достроить искомую фигуру до прямоугольника.
2. Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника.
3. Из площади прямоугольника вычесть сумму площадей всех лишних фигур.

Бывает, что не так-то просто рассчитать, сколько клеток в нужном отрезке. Вот смотри, треугольник:

Вроде бы даже прямоугольный и S=12⋅abS=​2​​1​​⋅ab, но чему тут равно aa, и чему равно bb? Как узнать? Применим для полной ясности оба способа

I способ.

Найдем по теореме Пифагора из ΔADC а по теореме Пифагора из ΔBCE. На  листе в клетку легко посчитать длину катетов.

Итак:

Значит,

Теперь

Значит,

Подставляем в формулу:

Значит,

II способ

Нужно окружить нашу фигуру прямоугольником. Вот так:

 

Получился один (нужный) треугольник внутри и три ненужных треугольника снаружи. Но площади этих ненужных треугольников легко считаются на листе в клетку. Посчитаем их, а потом просто вычтем из целого прямоугольника.

Итак,                      

Почему же этот способ лучше? Потому что он работает и для любых фигур. К примеру, нужно посчитать площадь такой фигуры:

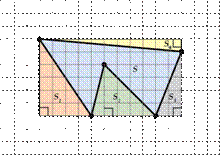Окружаем ее прямоугольником и снова получаем одну нужную, но сложную площадь и много ненужных, но простых.

А теперь чтобы найти площадь просто находим площадь прямоугольника и вычитаем из него оставшуюся площадь фигур на клетчатой бумаге.

 

Значит,

Вот и ответ: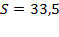

 

 

Модуль 3: Задачи с решением.

1. Найдите площадь четырёхугольника, изображённого на клетчатой бумаге
с размером клетки 1 см * 1 см. Ответ дайте в квадратных сантиметрах.

Решение:
Разобьём четырёхугольник диагональю РС на два треугольника. Диагональ эта хороша тем, что идёт под углом 45° к горизонту. Проведём через точки А и В прямые, параллельные диагонали.

 

Если на верхней прямой взять любую точку Т, то площадь треугольника РТС окажется равной площади треугольника РАС, т.к. основание РС у них общее,
а высоты, проведённые к РС, равны. Такие же рассуждения о точке К.

 

 

Таким образом, если удачно разместить точки Т и К, как на рисунке выше, то

S_ACBP = S_PAC + S_PBC = S_PTC + S_PKC = S_TKP = 0,5·6·3 = 9

 

Ответ: 9

Возможны и другие варианты расположения точек Т и К:

 

 

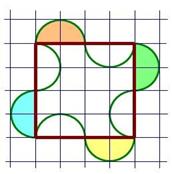
2. Найдите площадь фигуры, изображенной на рисунке, считая стороны квадратных клеток равными единице.

Решение:

Отрежем у данной фигуры все полукруглые части (выпуклости), которые выходят за рамки квадрата 4·4, и аккуратно упакуем их на свободные в квадрате места.
Площадь данной причудливой фигуры просто равна площади квадрата 4·4 = 16.
Ответ: 16

 

 

3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см * 1 см. Ответ дайте в квадратных сантиметрах.

Решение:

Опишем около неё прямоугольник.

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

Ответ: 4,5

 

 

4. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах.

5. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах.

---

Дата добавления: 2018-05-01; просмотров: 2575; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!