Решение уравнения наименьших квадратов
МИНИСТЕРСТВООБРАЗОВАНИЯИНАУКИ
РОССИЙСКОЙФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕГОСУДАРСТВЕННОЕАВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕУЧРЕЖДЕНИЕВЫСШЕГООБРАЗОВАНИЯ«ТЮМЕНСКИЙГОСУДАРСТВЕННЫЙУНИВЕРСИТЕТ»
Институтматематикиикомпьютерныхнаук
Кафедрапрограммногообеспечения
Курсоваяработа
подисциплине«Структурыиалгоритмыкомпьютернойобработкиданных»
натему:«Исследованиекачестваосновныхалгоритмовмашинногообучениядлярешениязадачиклассификации»
Выполнил:
Студентгруппы164-1
ПоляковИгорьАндреевич
Проверил:
_______________________ ст.преподавателькафедрыпрограммногообеспечения
ПавловаЕленаАлександровна
Оглавление
Введение. 3
Глава 1.Теоретические сведения. 4
1.1.Упрощенный байесовский классификатор. 4
1.2. Линейная регрессия. 7
1.3. Нейронная сеть. 11
Глава 2.Разработка приложений. 16
2.1. Используемые классы и методы Байесовского классификтора. 16
2.1.1. Демонстрация работы приложения для классификации пола. 17
2.2. Используемые классы и методы Линейной регрессии. 18
2.2.1. Демонстрация работы приложения для прогнозирования дохода. 19
2.3. Используемые классы и методы Нейронной сети. 19
2.3.1. Демонстрация работы приложения для классификации цвета. 21
Список литературы.. 23
Приложение 1. 24
Приложение 2. 25
Приложение 3. 29
Введение
Вмашинномобучениизадачаклассификацииотноситсякразделуобучениясучителем.Разделмашинногообучения,посвященныйрешениюследующейзадачи.Имеетсямножествообъектов(ситуаций)имножествовозможныхответов(откликов,реакций).Существуетнекотораязависимостьмеждуответамииобъектами,ноонанеизвестна.Известнаконечнаясовокупностьпрецедентов—пар«объект,ответ»,называемаяобучающейвыборкой.Наосновеэтихданныхвосстановливаетсязависимость,тоестьзадача в построенииалгоритма,способногодлялюбогообъектавыдатьточныйответ.Дляизмеренияточностиответовопределённымобразомвводитсяфункционалкачества.
|
|
|
Подучителемпонимаетсялибосамаобучающаявыборка,либотот,ктоуказалназаданныхобъектахправильныеответы.Существуеттакжеобучениебезучителя,в этом случаенаобъектахвыборкиответынезадаются.
Формулировказадачи
1. Изучитьосновныеалгоритмыклассификации.
2. Реализоватьодинизалгоритмовклассификации.
Цельработы
Цельюмоейработыбылоизучениекачестваалгоритмовклассификацииипрограммнаяреализациянескольких изних.
Существуютнесколькоосновныхвидовалгоритмовклассификациисобучающейвыборкой:
· Упрощенныйбайесовскийклассификатор
· Линейнаярегрессия
· Нейронные сети
Глава1.Теоретическиесведения
Упрощенныйбайесовскийклассификатор
ФормулаБайесапозволяетпоменятьместамипричинуиследствиевформулахсусловнымивероятностями:
|
|
|
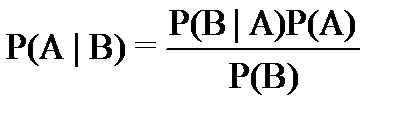
· P(A|B)–апостериорнаявероятностьданногоклассаc(т.е.данногозначенияцелевойпеременной)приданномзначениипризнакаx.
· P(A)–априорнаявероятностьданногокласса.
· P(B|A)–правдоподобие,т.е.вероятностьданногозначенияпризнакаприданномклассе.
· P(B)–априорнаявероятностьданногозначенияпризнака.
ПустьвкачествеAунасбудетрассматриватьсянекотороемножествоклассовC,которыммогутпринадлежатьнашиобъекты;авкачествеB–наборпризнаков(векторпредикторов)X1,X2,…,XnX1,X2,…,Xn,позначениямкоторыммыбудемпытатьсяотнестилюбойобъекткодномуизклассов.ВэтихобозначенияхформулаБайесаперепишетсяследующимобразом:
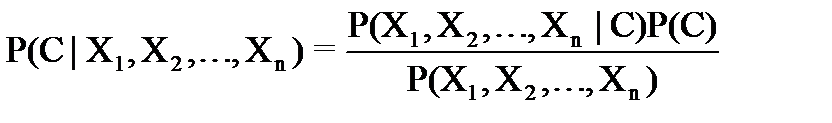
Если,например,рассматриваютсятрикласса:“флет”,“трендвверх”,“трендвниз”,авкачествепредикторов(наблюдаемогонаборапризнаков)выступаетденьнеделиивчерашнеесостояниетренда,тоформулаБайесаприметвид:
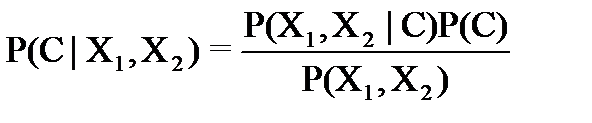
гдеслучайнаявеличинаCможетприниматьтризначения0(флет),1(uptrend,трендвверх)и-1(downtrend,трендвниз);предикторX1принимаетзначенияMn,Tu,Wd,ThиFr(рабочиеднинеделиспонедельникадопятницы);предикторX2–тежезначения,чтоиC(флет,трендвверхилитрендвниз,ноимеетсяввидунаправлениерынкавтечениепредыдущегодня).
|
|
|
ВчислителеP(C)–этоаприорныевероятноститого,чтолюбойизрассматриваемыхобъектов(споканеизвестнымипризнаками)окажетсяпринадлежащимданномуклассу.Внашемпримеретритакихвероятности,дляфлетаидлятрендовобоихнаправлений:P0,P1,иP−1.
ЗнаменательвформулеБайесаP(X1,X2)–вероятноститого,чтонаугадвзятыйобъектбудетиметьзаданныйнаборзначенийпризнаков.Внашемпримере15такихвероятностей:P(Mn,-1),P(Tu,-1),…,P(Mn,0),…,P(Fr,1).
P(X1,X2∣C)–этоусловныевероятноститого,чтообъект,принадлежащийданномуклассу,имеетзаданныйнаборпризнаков.Внашемпримере5⋅3⋅3=45такихвероятностей:
P(Mn,−1∣1),P(Tu,−1∣−1),…,P(Fr,1∣1).
Если,допустим,известнывсевероятности,стоящиевформулеБайесасправаотзнакаравенства,тогдаможнорассчитатьусловнуювероятностьслева.Тогдаполюбомунаборузначенийпризнаковможнонайтивероятностьотнестипредъявленныйобъектккаждомуизклассов.Какаявероятностьокажетсябольше,тотклассмыивыберем.ВероятностьвзнаменателеформулыБайесаможнонерассматривать,посколькуонанезависитоттого,ккакомуклассупринадлежиттотилиинойобъект.Чтобывыбратьнаибольшеезначениеизвсехрассчитанных,намдостаточнознатьтольковероятности,стоящиевчислителе.
Байесовскийклассификатортребуетобучения:мыпредъявляемемунаборобъектовсразличнымизначениямипризнаков(внашемпримереэтоизмененияцензакакой-либоотрезокистории)исообщаем,ккакомуклассудолженбытьотнесёнкаждыйизэтихобъектов.Описанныйпроцессназываетсяобучениемсучителем(учитель–этотот,ктознает,ккакомуклассудолжныбытьотнесеныобъекты).Врезультатеобученияклассификатордолженнайтизначениявсехвероятностей,стоящихвформулеБайесасправаотзнакаравенствавчислителе.
|
|
|
Нозадачуможноупростить,еслипредположить,чтовсепризнакинезависимыдруготдруга.Тогдаможновероятностьсложногособытиязаписатьввидепроизведениявероятностейкаждогособытиявотдельности: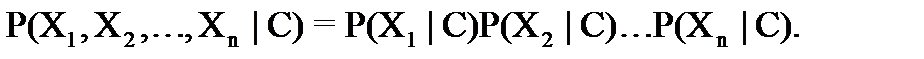 
Что это даёт?Проще найти n одномерных функций, чем одну n-мернуюфункцию.Для нашего примера вместо 45-ти условных вероятностей P(X1,X2∣C)P(X1,X2∣C)надооценитьпоэкспериментальнымданнымизобучающейвыборкинезависимодруготдруга15значенийP(X1∣C)P(X1∣C)(5рабочихднейнеделина3состояниярынка)и9значенийP(X2∣C)P(X2∣C)(трисостояниярынкавчеранатрисостояниясегодня),т.е.всего 24 искомых параметров вместо 45.При увеличении размерности задачи (количества признаков) выигрыш ещё более заметен.
Такимобразом,упрощенныйбайесовскийклассификатор—этопростойвероятностныйклассификатор,основанныйнапримененииТеоремыБайесас(наивными)предположениямионезависимостипредикторов:
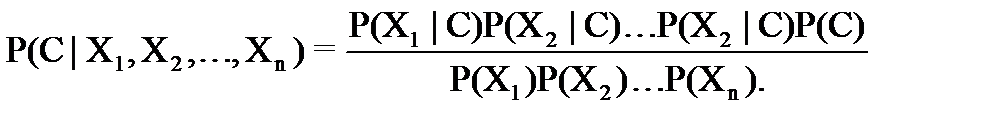
Из основных преимуществ—простотареализацииинизкиевычислительныезатратыприобучениииклассификации.Вслучаях,когдапризнакинезависимы(илипочтинезависимы),наивныйбайесовскийклассификатороптимален.Основнойнедостаток—относительнонизкоекачествоклассификациивбольшинствереальныхзадач.Чащеониспользуетсяиликак«примитивный»эталондлясравненияразличныхмоделейалгоритмов,иликакэлементарный«строительныйблок»валгоритмическихкомпозициях подобных примеру на Рис 1.
| Начало |
| Генерация обучающей выборки |
| Получение входных данных в виде списка признаков объекта |
| Вычисление вероятности каждого из классов с учетом всех признаков |
| Вычисление полных вероятностей для каждого класса |
| Получение вероятности полных классов |
| Конец |
Рис 1. Блок-схема алгоритма наивной байесовской классификации.
Преимуществабайесовскогоподхода.
· Байесовскоерешающееправилооптимально,выписываетсявявноманалитическомвиде,легкореализуетсяпрограммно.Наегоосновестроятсямногиеметодыклассификации.
· Приклассификацииобъектазаоднооцениваютсяаприорныевероятностиегопринадлежностикаждомуизклассов.Этаинформацияиспользуетсявомногихприложенияхдляоценкирисков.
· Байесовскоерешающееправилоудобноиспользоватьвкачествеэталонапритестированииалгоритмовклассификациинамодельныхданных.
Недостаткибайесовскогоподхода.
· Модельточналишьвслучае,когдавыполняетсяпредположениеонезависимости.Впротивномслучае,строгоговоря,вычисленныевероятностиуженеявляютсяточными(идажеболеетого,ихсуммаможетнеравнятьсяединице,из-зачеготребуетсянормироватьрезультат).Однаконапрактикенезначительныеотклоненияотнезависимостиприводятлишькнезначительномуснижениюточности,идажевслучаесущественнойзависимостимеждупеременнымирезультатработыклассификаторапродолжаеткоррелироватьсистиннойпринадлежностьюобразакклассам.
· Есливтестовомнабореданныхприсутствуетнекотороезначениекатегорийногопризнака,котороеневстречалосьвобучающемнабореданных,тогдамодельприсвоитнулевуювероятностьэтомузначениюинесможетсделатьпрогноз.Этоявлениеизвестноподназванием«нулеваячастота».Даннуюпроблемуможнорешитьспомощьюсглаживания.ОднимизсамыхпростыхметодовявляетсясглаживаниепоЛапласу.
Линейнаярегрессия
Линейная регрессия — это алгоритм контролируемого машинного обучения, который прогнозирует результат, основанный на непрерывных функциях. Линейная регрессия универсальна в том смысле, что она имеет возможность запускаться с одной входной переменной (простая линейная регрессия) или с зависимостью от нескольких переменных (множественная регрессия). Если ищется связь между одной входной (независимой) и одной выходной (зависимой) переменными, то имеет место простая линейная регрессия. Для этого определяется уравнение регрессии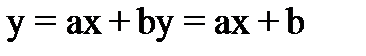 
и строится соответствующая прямая, известная как линия регрессии. Коэффициенты a и b, называемые также параметрами модели, выбираются таким образом, чтобы сумма квадратов отклонений точек, соответствующих реальным наблюдениям данных, от линии регрессии, была бы минимальной. Подбор коэффициентов производится по методу наименьших квадратов.
Если ищется зависимость между несколькими входными и одной выходной переменными, то имеет место множественная линейная регрессия. Соответствующее уравнение имеет вид:
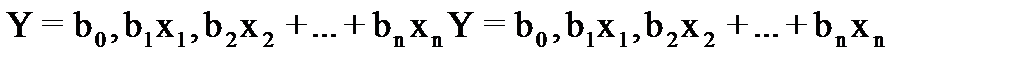
где n – число входных переменных (предикторов). Очевидно, что в данном случае модель будет описываться не прямой, а гиперплоскостью. Коэффициенты уравнения множественной линейной регрессии подбираются так, чтобы минимизировать сумму квадратов отклонения реальных точек данных от этой гиперплоскости.
Линейная регрессия на примере графикарис. 2. Данные на этом графике представляют прогнозируемый ежегодный доход на основе всего одной переменной — стажа работы. Каждая из темно-серых точек соответствует точке данных. Первый слева элемент данных соответствует стажу = 10 и доходу = 32.06. Линейная регрессия находит два коэффициента: один свободный и один для стажа. Значения коэффициентов равны 27.00 и 0.43.
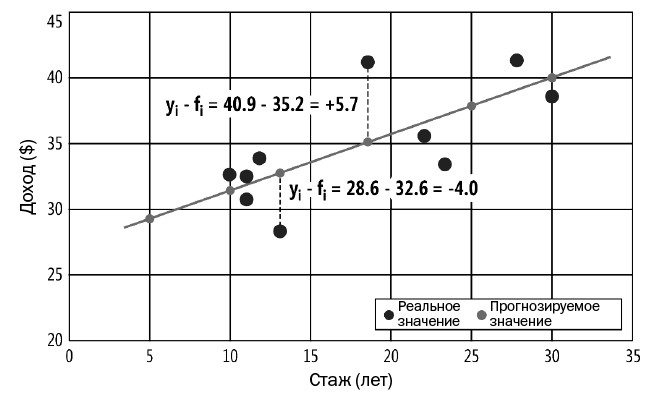
Рис. 2. Линейная регрессия с одной независимой переменной
Значения коэффициентов определяют уравнение прямой, показанное светло-серым цветом на рис. 2. Эта линия (коэффициенты) минимизирует сумму квадратичных отклонений между точками реальных данных (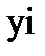 
) и точками спрогнозированных данных ( 
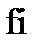). Два из десяти отклонений отображаются пунктирными линиями на рис. 2. Первым из этих отклонений является 
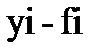= 28.6 – 32.6 = –4.0. Отклонения могут быть как положительными, так и отрицательными. Если бы отклонения не были квадратичными, отрицательные и положительные значения могли бы взаимно уничтожаться.
Решение уравнения наименьших квадратов
Если в задаче линейной регрессии имеются n переменных-предикторов, тогда нужно найти n+1 значений коэффициентов — по одному на каждый предиктор плюс свободный член. В демонстрационной программе используется самый базовый метод для нахождения значений коэффициентов. Эти значения даются с использованием приведенного ниже уравнения.
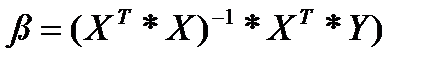
Буква «бета» представляет значения коэффициентов. Буква X представляет матрицу плана(просто матрица с данными, в которой все значения в ведущем столбце содержат 1.0). Буква X верхнего регистра в степени T означает транспонирование матрицы плана. Символ * обозначает перемножение матриц. Степень –1 указывает на обращение матрицы. Буква Y верхнего регистра — вектор-столбец (матрица с одним столбцом) значений зависимой переменной.
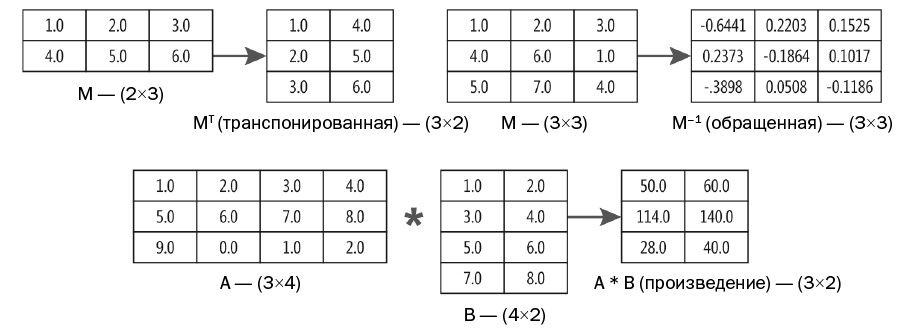
Рис. 3. Три матричные операции, используемые при нахождении коэффициентов линейной регрессии
Вычисление R-квадрата
R-squared (R-квадрат, или коэффициент детерминации) является мерой того, насколько хорошо точки реальных данных соответствуют вычисленной линии регрессии. В математических терминах R-квадрат определяется как R2 = 1 – (SSres / SStot). Член SSres обычно называется остаточной суммой квадратов (residualsumofsquares). Это сумма квадратов разности (squareddifferences) между реальными и предсказанными Y-значениями, как иллюстрирует график на рис. 2. Член SStot — это общая сумма квадратов (totalsumofsquares). Этот член является суммой квадратов разности между каждым реальным Y-значением и средним всех реальных Y-значений.
Показатель R-squared в линейной регрессии также называется коэффициентом детерминации и имеет отношение (но отличается от него) к другому статистическому показателю с названием «r-squared» («малый r-квадрат»). Интерпретация R-квадрата не совсем однозначна и зависит от предметной области конкретной задачи. В естественных и общественных науках, где данные, как правило, запутанные и неполные, значение R-квадрата от 0.6 и выше часто трактуется как довольно хорошее.
| Начало |
| Генерация обучающей выборки |
| Создание матрицы плана |
| Нахождение коэффициентов |
| Вычисление R-квадрата |
| Прогнозирование результата |
| Конец |
Рис 4. Блок-схема алгоритма классификации линейной регрессии.
Преимущества линейной регрессии
· Простота вычислительных алгоритмов.
· Наглядность и интерпретируемость результатов (для линейной модели).
Недостатки линейной регрессии
· В реальных применениях можно считать, что модель пригодна, если параметры изучаемого объекта не слишком отличаются от средних значений этих же параметров для исходного набора данных. Могут возникнуть (и возникнут) проблемы, если предикторы сильно коррелированы между собой.
· Невысокая точность прогноза (в основном - интерполяция данных).
· Субъективный характер выбора вида конкретной зависимости (формальная подгонка модели под эмпирический материал)
· Отсутствие объяснительной функции (невозможность объяснения причинно-следственной связи).
Нейронная сеть
Искусственная нейронная сеть (ИНС) — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Первой такой попыткой были нейронные сети У. Маккалока и У. Питтса[1]. После разработки алгоритмов обучения получаемые модели стали использовать в практических целях: в задачах прогнозирования, для распознавания образов, в задачах управления и др.
В качестве образов могут выступать различные по своей природе объекты: символы текста, изображения, образцы звуков и т. д. При обучении сети предлагаются различные образцы образов с указанием того, к какому классу они относятся. Образец, как правило, представляется как вектор значений признаков. При этом совокупность всех признаков должна однозначно определять класс, к которому относится образец. В случае, если признаков недостаточно, сеть может соотнести один и тот же образец с несколькими классами, что неверно. По окончании обучения сети ей можно предъявлять неизвестные ранее образы и получать ответ о принадлежности к определённому классу.
Топология такой сети характеризуется тем, что количество нейронов в выходном слое, как правило, равно количеству определяемых классов. При этом устанавливается соответствие между выходом нейронной сети и классом, который он представляет. Когда сети предъявляется некий образ, на одном из её выходов должен появиться признак того, что образ принадлежит этому классу. В то же время на других выходах должен быть признак того, что образ данному классу не принадлежит. Если на двух или более выходах есть признак принадлежности к классу, считается, что сеть «не уверена» в своём ответе.
В рассматриваемом примере используется архитектура персептрона с одним скрытым слоем, (рис.5) состоящая из трёх типов элементов, а именно: поступающие от датчиков сигналы передаются ассоциативным элементам, а затем реагирующим элементам. Таким образом, персептроны позволяют создать набор «ассоциаций» между входными стимулами и необходимой реакцией на выходе.
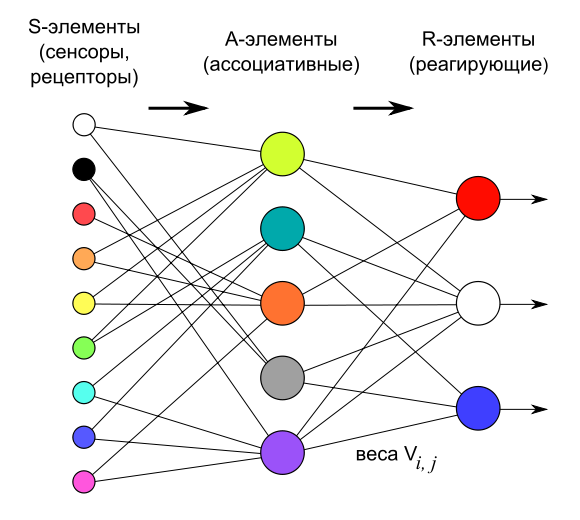
Рис. 5.Логическая схема персептрона с тремя выходами
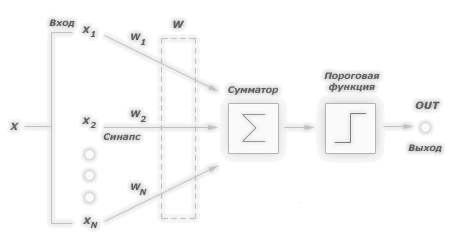
Рис. 6.Пример обучения персептрона
Оптимизация методом роя частиц
Алгоритм ParticleSwarmOptimization (PSO) основывается на концепции социального взаимодействия при решении проблем, предполагает нахождение локального экстремума, изменение опыта частицы находящейся в N-мерном пространстве для возможности передачи соседним сигнала изменения направления. В модели PSO каждая частица обладает вектором скорости и вектором позиции. При оптимизации N-мерной функции такие векторы имеют размерность N. Как и в биологической жизни, предполагается, что каждая частица регулирует свои векторы позиции и скорости в соответствии с собственным опытом (когнитивная составляющая), а также по информации, полученной от других членов социума (социальный опыт). Когнитивный опыт частицы понимается как ее знание о лучшей позиции, в которой она сама находилась, а социальное знание частицы – как знание о лучшей позиции, через которую прошла одна из частиц в одной группе с ней. В задаче оптимизации лучшая позиция частицы понимается как позиция, в которой минимизируется значение функции.
Таким образом, состояние каждой частицы роя характеризуется: 1. Тремя N-мерными векторами: • Х – текущая позиция частицы в поисковом пространстве; • G – лучшая позиция, найденная всем роем; • v – скорость движения частицы. 2. Двумя скалярными значениями, описывающими качество решения задачи: • P – фитнес-частицы (значение целевой функции в текущей позиции); • G – фитнес-группы, в которую входит частица (значение целевой функции в лучшей позиции). Изменение положения частицы задается простым добавлением v-вектора к X-вектору: Xi = Xi + vi. (8.1) Изначально значение вектора скорости генерируется случайным образом в пределах [–vmax, vmax], где vmax – максимально допустимое значение. Скорость частицы модифицируется по формуле vi = vi + c1r1(G – Xi ) + c2r2(Pi – Xi ), (8.2) где i – номер частицы; vi – вектор скорости; Xi – вектор позиции частицы; Pi – вектор лучшей позиции, которой достигала частица; G – вектор лучшей позиции, которой достигала группа из I частиц; с1, с2 – константы скорости обучения, управляющие соответствен- но социальной и познавательной компонентой; r1, r2 – случайные числа в диапазоне [0, 1], которые служат для поддержания разных траекторий частиц при поиске. Константы скорости обучения контролируют степень важности индивидуального познания и социального знания. Частица одновременно обновляет свою позицию относительно лучшей позиции группы и собственной лучшей позиции, которая была в прошлом. 237 Если с2 имеет преобладающее значение, то частица будет обследовать узкую область поискового пространства, а если преобладает с1, то происходит поиск в большом пространстве. В формулу (8.2) может вводиться фактор инерции W: vi = Wvi + c1r1(Pi – Xi ) + c2r2(G – Xi ). (8.3) Вначале фактор инерции W = 1, а потом он постепенно уменьшается во времени по формуле W= Wmax – (Wmax – Wmin)n/N, где n – номер текущей итерации; N – заданное число итераций. При инициализации частицы распределяются случайным образом в поисковом пространстве, их скорость получает случайные значения в допустимом диапазоне. Таким образом, работу алгоритма оптимизации PSO можно описать Рис. 6
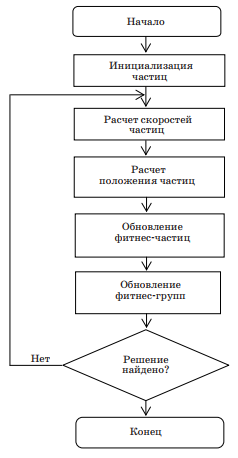
Рис. 6.Алгоритм оптимизации роем частиц
| Начало |
| Генерация обучающей выборки |
| Создание тренировочных и тестовых матриц с разделением 80%-20% |
| Тренировка с использованием PSO |
| Нахождение и загрузка лучших весов |
| Анализ точности нейронной сети на тестовых данных |
| Конец |
Рис 7. Блок-схема алгоритма классификации нейронной сети.
Дата добавления: 2018-05-01; просмотров: 163; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!