Предел функции на бесконечности.

⇐ ПредыдущаяСтр 5 из 7Следующая ⇒

Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число d>0, что для всех

х: ïхï>d выполняется неравенство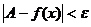

Обозначение: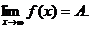

Основные правила вычисления пределов

Теорема 1. 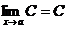, где С = const.

Теорема 2.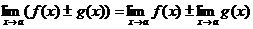

Теорема 3.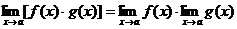

Следствие.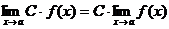

Теорема 4. 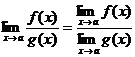при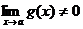

Теорема 5. Еслиf(x)>0 вблизи точки х = а и 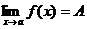, то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.

Теорема 6. Еслиg(x) £f(x) £u(x) вблизи точки х = а и 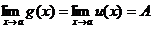, то и .

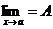Замечательные пределы.

Первый замечательный предел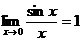

Второй замечательный предел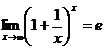

Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.

Кроме, изложенных выше, пределов можно записать следующие полезные на практике соотношения: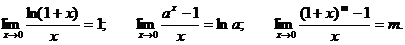

Пример. Найти предел: .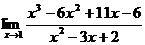

Решение: если напрямую подставить вместо х предельное значение 1, тогда вверху и внизу получатся 0 – это называется неопределенностью (записывается как 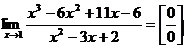) и эту неопределенность необходимо раскрыть чтобы решить предел (вычислить, т.е. получить ответ в виде числа). Для раскрытия неопределенностей такого вида сделаем следующее:

1) Разложим числитель и знаменатель,данной дроби на множители. В знаменателе по правилам нахождения корней квадратного уравнения, т.е.ах² + bх + с = 0- квадратное уравнение в общем виде, где а,b, с – коэффициенты уравнения (произвольные числа)

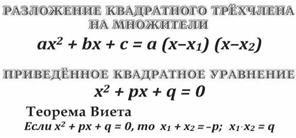т.е. для 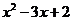= 0, получим корни х₁ = 1, х₂ = 2. А в числителе по правилам нахождения корней кубического уравнения: 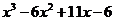= 0

2) Запишем предел следующим образом =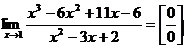

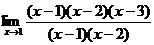
3) сокращаем одинаковые скобки, получаем

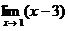
следовательно, неопределенность раскрыта и

4) можно подставить предельное значение на место х, т.е. .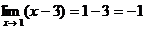

Пример. Найти предел: .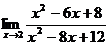

Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби по правилам нахождения корней квадратного уравнения, т.е.

ах² + bх + с = 0- квадратное уравнение в общем виде, где а,b, с – коэффициенты уравнения (произвольные числа)

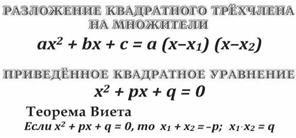
Т.е. 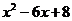= 0 и находим корни х₁ = 2, х₂ = 4, следовательно, разложением на множители получим: 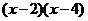. Аналогично для знаменателя: 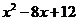= 0 получим: .

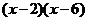Тогда .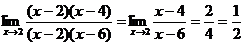

Пример. Найти предел: .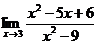

Решение: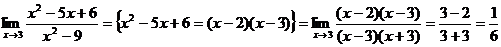

Пределы с неопределенностью вида и метод их решения

Рассмотрим группу пределов, когда 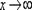, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Пример. Найти предел: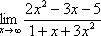

Решение: Согласно нашему правилу попытаемся подставить бесконечность¥ в функцию на место неизвестных, т.е. вместо всех х.Получим неопределенность вида . Для раскрытия неопределенностей такого типа необходимо в числителе и знаменателе разделить многочлены на х старшей степени, т.е.

Сначала мы смотрим на числитель и находимхв старшей степени: 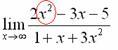Старшая степень в числителе равна 2.

Теперь смотрим на знаменатель и тоже находим х в старшей степени: 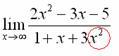Старшая степень знаменателя равна 2.Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий:для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на х в старшей степени. Разделим числитель и знаменатель нах²:

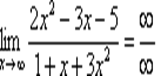
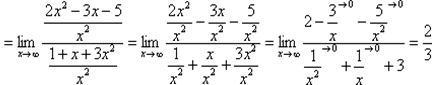
Для пределов такого вида запишем общее правило:

Общий вид предела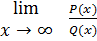

где Р(х) = а₀хⁿ + a₁xⁿ^-1+ …+ a_n–многочлен стоящий в числителе, а Q(х) = b₀х^m + b₁x^m^-1+ …+ b_m – многочлен, расположенный в знаменателе.

Тогда решение такого предела:

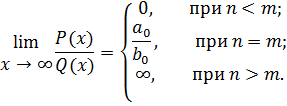
Дата добавления: 2018-05-01; просмотров: 375; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 Следующая ⇒

Мы поможем в написании ваших работ!