Прямийхід — зводимоматрицю до трикутноговигляду

Стр 1 из 2Следующая ⇒

Операції над множинами

1) Об’єднання (АUB)

2) Переріз (А B)

3)Різниця (А-В)

3) Диз’юнктивна сума множин (А В =В А)

Тотожності алгебри множин

1. Комутативний (переставний) закон ( U=+. ∩=- )
А U B = В U А;
А ∩ В = В ∩ А;

2. Асоціативний (сполyчний) закон. ( U=+. ∩=- )
А ∩ (В ∩ С) = (А ∩ В) ∩ С
А U (В U С) = (А U B) U С

3. Дистрибутивний (розподільний) закон. ( U=+. ∩=- )
А U (В ∩ С)=(А U B) ∩ (А U С)
А ∩ (В U С)=(А ∩ В) U (А ∩ С)

В-ті U та 0

4.1. А U 0 = A

4.2. A U Ā = A

4.3. A U U =U

4.4. 0 = U

4.5. A∩ U = A

4.6. A∩ A = 0

4.7. A∩ 0 = 0

4.8. Ū = 0

Закон самопоглинання

AU A = AA∩ A = A

Закон поглинання

A U (A∩ B) = A A∩(A U B) = A

7.ТеоремадеМоргана

A U B = Ā ∩ B A ∩ B =Ā U B

Действиянадматрицами

Сложение матриц:

Вычитание и сложение матриц сводится к соответствующим операциям над их элементами.Операция сложения матриц вводится только для матриц одинакового размера, т. е. для матриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов.
С=А+В
c_ij =a_ij +b_ij
Аналогично определяется разность матриц.

Умножение матрицы на число:

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Произведением матрицы А на число k называется матрица В, такая что b_ij = k × a_ij
В=k×A
b_ij =k×a_ij
Матрица - А = (-1) × А называется противоположной матрице А.

Определительматрицы

Де - Мінор

Матрицяназивається виродженою, якщоїївизначникдорівнюєнулю, авіншомувипадку невиродженою.

Визначник 2×2 матриці

Щобзнайтивизначник матриці, множимоелементи головноїдіагоналі тавіднімаємодобутокелементівпобічноїдіагоналі:

Визначник 3×3 матриці

Щобзнайтивизначник матриці, будуємошістьдобутків таким чином:

Обратная (Обернена) матрица

При изучении высшей математики часто требуется решить обратную матрицу. В этой статье я постараюсь детально объяснить, что такоематрица обратная даннойи как ее найти.

Обратная матрица есть только у невырожденной матрицы, т.е. у той матрицы, определитель которой не равен нулю. У вырожденной матрицы(определитель=0) обратной матрицы не существует.

Матрица обратная данной - это матрица, при умножении на которую данной в результате получается единичная матрица.

Условие обратной матрицы

Итак, если матрица получилась вырожденной, то на этом заканчиваем, т.к. решить обратную матрицу невозможно.

В противном случае, приступим к заполнению обратной матрицы. Для этого надо найти дополнения. Их количество всегда равно числу элементов матрицы. Если матрица третьего порядка, значит у нее 9 элементов, у каждого свое дополнение и все эти дополнения надо искать.

Покажу на примере схемы, как найти дополнение элемента, стоящего в первой строке второго столбца, значит элементы, стоящие в первой строке и втором столбце надо вычеркнуть. Оставшиеся элементы (их 4) - записываем в новый определитель, умноженный на (-1) в степени (1+2), где 1 и 2 -номера строки и столбца.

После нахождения всех дополнений составляем обратную матрицу, она представляет собойтранспонированную матрицу к той, которая составлена из полученных дополнений, деленная на определитель исходной матрицы. Вот почему важно, чтобы матрица была невырожденной (на нуль ведь делить нельзя).

Рассмотрим на примере нахождение обратной матрицы:

Пусть дана матрица В:

Найдем ее определитель:

Определитель равен 232, это не ноль, значит матрица невырожденная и для нее можно найти обратную матрицу.

Для этого найдем 9 дополнений:

Дополнение для элемента, стоящего в первой строке первого столбца:

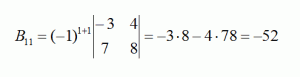
Дополнение для элемента, стоящего в первой строке второго столбца:

Дополнение для элемента, стоящего в первой строке третьего столбца:

Теперь определим следующие три дополнения для второй строки:

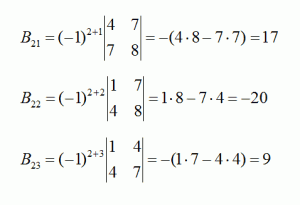
И последние три для третьей строки:

Теперь составим обратную матрицу:

Розклад детермінанта за елементами рядка (стовпця)

Детермінант Δ п-го порядку дорівнює сумі всіх добутків елементів довільного рядка або стовпця на їх алгебраїчні доповнення тобто:

Δ=a_i1·A_i1+ a_i2·A_i2+…+ a_in·A_in; (3.2)

або:

Δ=a_1j·A_1j+ a_2j·A_2j+…+ a_nj·A_nj. (3.3)

Формулу (3.2) називають розкладом детермінанта за елементами і-го рядка, а формулу (3.3) - розкладом цього детермінанта за елементами j-го стовпця.

Опорныйэлемент

Опорным элементом матрицы называется 1ый ненулевой элемент этой строки.

В 1й строке это 1, во 2й это 2, в 3й – 5, в 4й его нет.

Приєднана матриця

Приє́днаною до матриці A, називається матриця створена з алгебраїчнихдоповнень для відповіднихелементівпервісноїматриці, і транспонована потому.

де A_ij — алгебраїчнедоповнення елемента a_ij даноїматриці A.

Приклад

Нехай матриця

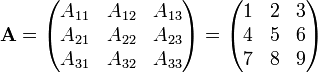Їїприєднанаматрицямаєвигляд:

Мінор

Визначникматриці, яка одержується з 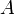викреслюваннямвсіхрядків та стовпців, окрімвибраних, називається мінором -го порядку, розташованим в рядках з номерами та стовпцях з номерами .

Знаходженнямінорів:

Алгебраїчне доповнення і мінор

Рассмотрим на примере нахождение алгебраического дополнения элементов матрицы:

Пусть дана матрица А:

Найдем алгебраические дополнения для двух элементов:

1. для элемента, который стоит в первой строке, первом столбце

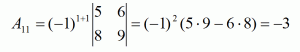
2. для элемента, который стоит в третьей строке, втором столбце

А теперь используя алгебраическое дополнение матрицы найдем определитель матрицы А , используя теорема Лапласа:

Пусть дана матрица А:

Разложим по первой строке:

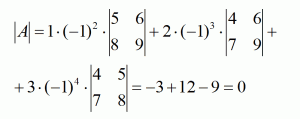
Обратите внимание еще раз, как раскладывалась матрица, как находилосьалгебраическое дополнение матрицы:

Мінором -го порядку матриці 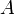називається визначникматриці, утворенийелементами на перетині стовпців та рядків.

Алгебраїнимдоповненнямелемента називаютьмінорцьогоелемента, взятий зі знаком тобто

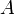§ Мінор квадратноїматриці — визначникматриці, отриманий шляхом викреслювання рядка 2 та стовпчика 3:

§ Знайтиалгебраїчнідоповненняелементів а₂₁ та а₃₃ визначника

Розв'язок:

Алгебраїчнідоповнення до елементів а₂₁ та а₃₃ позначимо А₂₁ та А₃₃, відповідно.

Знаходженнямінорів:

Підставимоцізначеннямінорів у відповіднірівності (4), одержимо шуканіалгебраїчнідоповнення

А₂₁=(-1)²⁺¹ М₂₁= -13

А₃₃=(-1)³⁺³ М₃₃= 5

Методи обернення матриць

Метод Гауса

Прямийхід: Шляхом елементарнихперетвореньрядків (додавань до рядка іншого рядка, помноженого на число, і перестановок рядків) матриця приводиться до верхньотрикутноговигляду.

Зцього моменту починається зворотнийхід.

Зостанньогоненульовогорівняннявиражаємокожну з базисних змінних через небазисні і підставляємо в попереднірівняння. Повторюючицю процедуру для всіхбазиснихзмінних, отримуємо фундаментальнийрозв'язок.

Приклад

Запишемо розширенуматрицю системи

Прямийхід — зводимоматрицю до трикутноговигляду

Обнулимокоефіцієнтипри 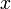в другому та третьму рядку. Для цьоговіднімемовід них перший рядок помноженийна та , відповідно:

Теперобнулимокоефіцієнтпри в третьому рядку, віднявшивіднього, другий рядок помножений на :

Тепернашаматрицямає трикутнийвигляд, отже ми закінчилипрямийхід.

Дата добавления: 2018-04-15; просмотров: 210; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!