Модуль 1. Электростатика. Постоянный электрический ток
Занятие 1. Взаимодействие заряженных тел. Закон Кулона. Напряженность электрического поля. Теорема Остроградского-Гаусса. Потенциал электростатического поля
Краткие теоретические сведения
Основные формулы
Закон сохранения электрического заряда:
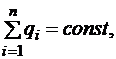 где
где 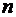 - число зарядов.
- число зарядов.
Напряженность электрического поля:
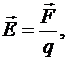
где 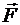 - сила, действующая на точечный положительный заряд
- сила, действующая на точечный положительный заряд 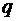 , помещенный в данную точку поля.
, помещенный в данную точку поля.
Закон Кулона:
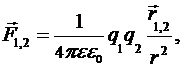
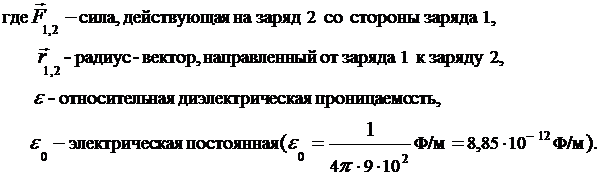
Напряженность поля точечного заряда:
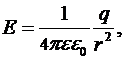
где q – заряд, создающий поле, 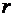 - расстояние от точечного заряда до рассматриваемой точки.
- расстояние от точечного заряда до рассматриваемой точки.
Принцип суперпозиции электрических полей:
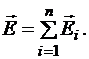
Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью на расстоянии 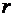 от ее оси:
от ее оси:
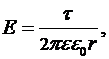
где 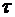 - линейность заряда (
- линейность заряда ( 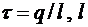 - длина нити, на которой распределен заряд
- длина нити, на которой распределен заряд 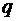 ).
).
Напряженность поля равномерно заряженной бесконечной пластины с поверхностной плотностью заряда 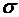 :
:
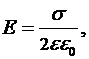
где 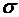 - поверхностная плотность заряда (
- поверхностная плотность заряда ( 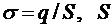 - площадь поверхности, по которой распределен заряд
- площадь поверхности, по которой распределен заряд 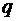 ).
).
Напряженность поля между двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями с одинаковой по модулю плотностью заряда 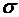 :
:
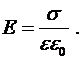
Напряженность электрического поля равномерно заряженного шара:
а) для точек внутри шара: 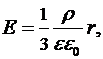
где 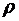 - объемная плотность зарядов,
- объемная плотность зарядов, 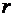 - расстояние от центра шара до рассматриваемой точки;
- расстояние от центра шара до рассматриваемой точки;
б) для точек вне шара:
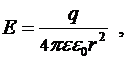 (*)
(*)
где 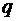 - полный заряд шара.
- полный заряд шара.
|
|
|
Напряженность электрического поля 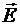 , создаваемого металлической сферой радиусом
, создаваемого металлической сферой радиусом 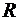 , несущей заряд
, несущей заряд 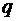 , на расстоянии
, на расстоянии 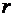 от центра сферы:
от центра сферы:
а) внутри сферы ( 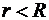 ):
): 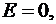
б) на поверхности сферы ( 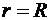 ):
): 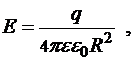
в) вне сферы ( 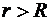 ) по той же формуле*, что и для точек вне шара.
) по той же формуле*, что и для точек вне шара.
Напряженность поля бесконечно длинного, равномерно заряженного цилиндра(для точек, находящихся вне цилиндра):
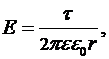
где 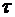 - линейная плотность заряда.
- линейная плотность заряда.
У поверхности любого проводника с постоянной поверхностной плотностью заряда 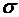 напряженность поля равна:
напряженность поля равна:
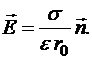
Напряженность поля диполя в точке, находящейся на расстоянии 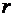 от середины плеча диполя:
от середины плеча диполя:
|
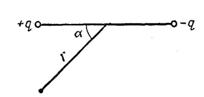
Электрический момент диполя:
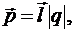
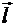 - плечо диполя (вектор
- плечо диполя (вектор 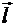 , проведенный от отрицательного заряда диполя к его положительному заряду).
, проведенный от отрицательного заряда диполя к его положительному заряду).
Вектор электрического смещения (вектор индукции) и напряженность полядля изотропной среды связаны соотношением:
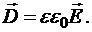
Теорема Остроградского-Гаусса. Поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью:
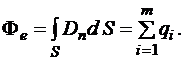
Потенциал электрического поля:
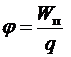 или
или 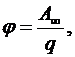
где 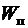 - потенциальная энергия точечного положительного заряда, помещенного в данную точку поля;
- потенциальная энергия точечного положительного заряда, помещенного в данную точку поля; 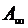 - работа сил поля по перемещению точечного положительного заряда из данной точки в бесконечность.
- работа сил поля по перемещению точечного положительного заряда из данной точки в бесконечность.
|
|
|
Разность потенциалов между двумя точками электрического поля:
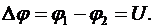
Потенциал электрического точечного заряда 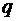 на расстоянии
на расстоянии 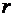 от него:
от него:
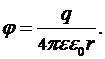
Потенциал электрического поля, создаваемого металлической сферой радиуса 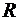 на расстоянии
на расстоянии 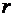 от центра сферы, несущей заряд
от центра сферы, несущей заряд 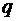 :
:
а) внутри и на поверхности сферы ( 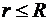 ):
):
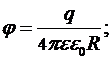
б) вне сферы ( 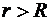 ):
):
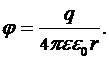
Связь потенциала с напряженностью:
а) в общем случае:
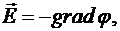
где 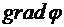 - градиент потенциала;
- градиент потенциала;
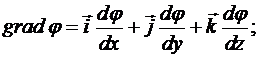
 - единичные векторы координатных осей OX, OY, OZ соответственно;
- единичные векторы координатных осей OX, OY, OZ соответственно;
б) в случае однородного поля:
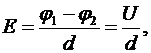
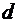 - расстояние между двумя эквипотенциальными поверхностями, имеющими потенциалы
- расстояние между двумя эквипотенциальными поверхностями, имеющими потенциалы 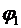 и
и 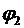 .
.
Работа, совершаемая электрическим полем при перемещении точечного заряда 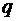 из одной точки поля, имеющую потенциал
из одной точки поля, имеющую потенциал 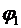 , в другую, имеющую потенциал
, в другую, имеющую потенциал 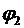 ,
,
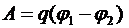 или
или 
где 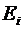 - проекция вектора напряженности
- проекция вектора напряженности 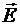 на направление перемещения;
на направление перемещения; 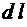 - величина перемещения.
- величина перемещения.
Вопросы для ответа у доски
1. Закон Кулона.
Изложите идею опытов Кулона по количественному изучению взаимодействия точечных зарядов. Единица заряда в СИ. Электрическая постоянная. Назовите основные единицы СИ. Дайте определение единицы заряда в СИ (кулона). Запишите закон Кулона в СИ.
|
|
|
2. Напряженность электрического поля. Единицы напряженности.
Дайте определение напряженности поля в данной точке. Единица измерения напряженности в СИ.
3. Поле диполя: а) случай, когда точка М находится на оси диполя; б) случай, когда точка М находится на перпендикуляре к оси диполя в центре его; в) общий случай.
Во всех случаях следует рассчитать величину напряженности, используя принцип суперпозиции полей, а также записать формулу в векторном виде.
4. Теорема Остроградского-Гаусса.
Введите понятие о потоке вектора напряженности. Рассчитайте поток вектора напряженности через сферу, центр которой совпадает с электрическим точечным зарядом. Обобщите полученный результат для случая системы точечных зарядов и произвольной поверхности. Сформулируйте теорему Остроградского-Гаусса.
5. Применение теоремы Остроградского-Гаусса для расчета полей: а) бесконечной равномерно заряженной плоскости; б) двух разноименно заряженных бесконечных плоскостей; в) бесконечного равномерно заряженного цилиндра; г) равномерно заряженного шара; д) равномерно заряженной сферы.
Во всех случаях необходимы рисунки, объяснение применения теоремы Остроградского-Гаусса, а также графики зависимости напряженности от расстояния.
|
|
|
6. Работа сил электростатического поля.
Получите формулу для работы в случае движения одного точечного электрического заряда в поле другого. Обобщите эту формулу для случая поля системы точечных зарядов. Покажите, что электростатическое поле является потенциальным.
7. Потенциал электростатического поля. Единица потенциала.
Получите формулу для потенциальной энергии взаимодействия двух точечных зарядов и проанализируйте ее. Обобщите эту формулу на случай заряда, находящегося в поле системы точечных зарядов. Введите понятие о потенциале. Единица потенциала в СИ.
8. Потенциал поля заряженной сферы.
Рассчитайте разность потенциалов в точках, находящихся за пределами и внутри сферы. Получите формулу для расчета потенциала сферы (шара). Покажите, что заряженная сфера (шар) является эквипотенциальной поверхностью.
Примеры решения задач
Задача 1.
Три одинаковых положительных заряда Q1=Q2=Q3 =1нКл расположены по вершинам равностороннего треугольника. Какой отрицательный заряд Q4 нужно поместить в центре треугольника, чтобы сила притяжения с его стороны уравновесила силы взаимного отталкивания зарядов, находящихся в вершинах?
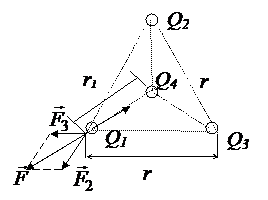 Решение.
Решение.
|
Поэтому заряд Q1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю:
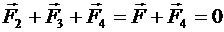 , (*)
, (*)
где 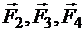 - силы, с которыми соответственно действуют на заряд Q1 заряды Q2, Q3 и Q4 ;
- силы, с которыми соответственно действуют на заряд Q1 заряды Q2, Q3 и Q4 ; 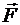 – равнодействующая сил
– равнодействующая сил 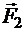 и.
и. 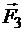 Так как силы
Так как силы 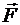 и
и  направлены по одной прямой, то векторное равенство (*) можно заменить суммой:
направлены по одной прямой, то векторное равенство (*) можно заменить суммой:
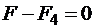 или
или 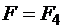 .
.
Выразив в последнем равенстве 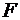 через
через 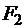 и
и 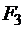 и, учитывая, что
и, учитывая, что 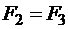 , получим:
, получим:
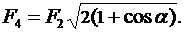
Применяя закон Кулона, и имея в виду, что Q1=Q2=Q3, найдём:
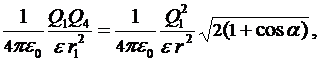 откуда
откуда 
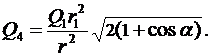
Из геометрических построений в равностороннем треугольнике следует, что:
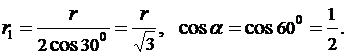
С учётом этого получим:
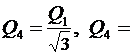 0,58 нКл.
0,58 нКл.
Отметим, что равновесие системы зарядов будет неустойчивым.
Ответ: 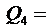 0,58 нКл.
0,58 нКл.
Задача 2.
Электрическое поле создано двумя точечными зарядами: Q1=30 нКл и Q2=-10нКл. Расстояние d между зарядами равно 20см. Определить напряженность электрического поля в точке, находящейся на расстоянии 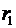 =15см от первого и на расстоянии
=15см от первого и на расстоянии 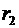 =10см от второго заряда.
=10см от второго заряда.
Решение.
Согласно принципу суперпозиции электрических полей, каждый заряд создаёт поле, независимо от присутствия в пространстве других зарядов. Поэтому напряженность 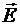 электрического поля в искомой точке может быть найдена как векторная сумма напряженностей
электрического поля в искомой точке может быть найдена как векторная сумма напряженностей 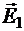 и
и 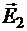 полей, создаваемых каждым зарядом в отдельности:
полей, создаваемых каждым зарядом в отдельности: 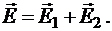
 Напряженности электрического поля, создаваемого в вакууме первым и вторым зарядами, соответственно равны:
Напряженности электрического поля, создаваемого в вакууме первым и вторым зарядами, соответственно равны:
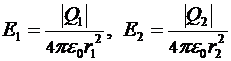 (*)
(*)
Вектор 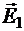 направлен по силовой линии от заряда Q1, так как заряд Q1 >0; вектор
направлен по силовой линии от заряда Q1, так как заряд Q1 >0; вектор 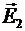 направлен также по силовой линии, но к заряду Q2, т.к. Q2<0 . Абсолютное значение вектора
направлен также по силовой линии, но к заряду Q2, т.к. Q2<0 . Абсолютное значение вектора 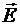 найдем по теореме косинусов:
найдем по теореме косинусов:
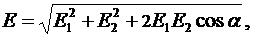 (**)
(**)
где угол a может быть найден из треугольника со сторонами 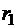 ,
, 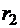 и d:
и d:
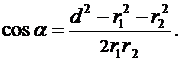
В данном случае во избежание громоздких записей вычислим отдельно значение 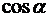 . По этой формуле найдем
. По этой формуле найдем 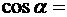 0,25.
0,25.
Подставляя выражения 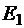 и
и 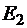 в формулы (*), а затем - в формулу (**), получаем:
в формулы (*), а затем - в формулу (**), получаем:
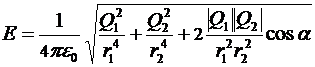 .
.
Подставив значения величин и произведя вычисления, найдем:
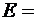 16,7кВ/м.
16,7кВ/м.
Ответ: 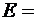 16,7кВ/м.
16,7кВ/м.
Задача 3.
Точечный заряд Q=25нКл находится в поле, созданном прямым бесконечным цилиндром радиусом R=1см, равномерно заряженным с поверхностной плотностью 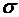 =2мкКл/м2. Определить силу, действующую на заряд, помещенный от оси цилиндра на расстояние
=2мкКл/м2. Определить силу, действующую на заряд, помещенный от оси цилиндра на расстояние 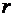 =10см.
=10см.
Решение.
Сила, действующая на заряд Q, находящийся в поле: 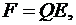
где 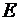 – напряженность поля в точке, в которой находится заряд Q. Как известно, напряженность поля бесконечно длинного равномерно заряженного цилиндра:
– напряженность поля в точке, в которой находится заряд Q. Как известно, напряженность поля бесконечно длинного равномерно заряженного цилиндра:
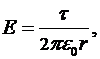
где 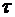 - линейная плотность заряда.
- линейная плотность заряда.
Выразим линейную плотность 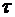 через поверхностную плотность
через поверхностную плотность 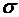 . Для этого выделим элемент цилиндра длиной
. Для этого выделим элемент цилиндра длиной 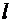 и выразим находящийся на нём заряд Q1 двумя способами:
и выразим находящийся на нём заряд Q1 двумя способами:
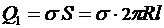 и
и 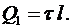
Приравняв правые части этих равенств, получим:
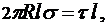 после сокращения получаем:
после сокращения получаем: 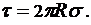
С учётом этого, формула 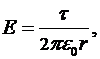 примет вид
примет вид 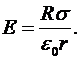 Подставив это выражение
Подставив это выражение 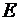 в
в 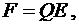 найдём искомую силу:
найдём искомую силу:

Выполнив вычисления, найдём:
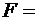 0,565мН.
0,565мН.
Направление силы совпадает с направлением вектора напряженности 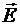 , а последний в силу симметрии (цилиндр бесконечно длинный) направлен перпендикулярно цилиндру.
, а последний в силу симметрии (цилиндр бесконечно длинный) направлен перпендикулярно цилиндру.
Ответ: 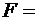 0,565мН.
0,565мН.
Задача 4.
Две концентрические проводящие сферы радиусами 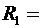 6см и
6см и 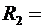 10см несут соответственно заряды
10см несут соответственно заряды 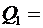 1нКл и
1нКл и 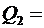 -0,5нКл. Найти напряженность
-0,5нКл. Найти напряженность 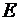 поля в точках, отстоящих от центра сфер на расстояниях
поля в точках, отстоящих от центра сфер на расстояниях 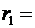 5см,
5см, 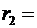 9см и
9см и 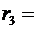 15см. Построить график
15см. Построить график 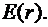
Решение.
|
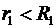 ), область II (
), область II ( 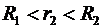 ), область III (
), область III ( 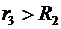 ).
).
|
|
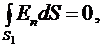 (*)
(*)
где  - нормальная составляющая напряженности электрического поля.
- нормальная составляющая напряженности электрического поля.
Из соображений симметрии нормальная составляющая  должна быть равна самой напряженности и постоянна для всех точек сферы, т.е.
должна быть равна самой напряженности и постоянна для всех точек сферы, т.е. 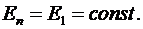 Поэтому ее можно вынести за знак интеграла. Равенство (*) примет вид:
Поэтому ее можно вынести за знак интеграла. Равенство (*) примет вид:
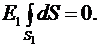
Так как площадь сферы не равна нулю, то 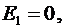 т.е. напряженность поля во всех точках, удовлетворяющих условию
т.е. напряженность поля во всех точках, удовлетворяющих условию 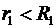 будет равна нулю.
будет равна нулю.
2. В области II проведем сферическую поверхность 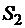 радиусом
радиусом 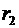 . Так как внутри этой поверхности находится заряд
. Так как внутри этой поверхности находится заряд 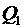 , то для нее, согласно теореме Остроградского-Гаусса, можно записать равенство:
, то для нее, согласно теореме Остроградского-Гаусса, можно записать равенство:

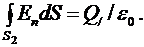 (1)
(1)
Так как 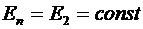 , то из условий симметрии следует:
, то из условий симметрии следует:
 или
или 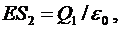 (2)
(2)
Откуда: 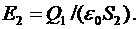
Подставив сюда выражение площади сферы, получим:
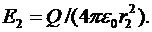 (3)
(3)
3. В области III проведем сферическую поверхность 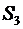 радиусом
радиусом 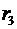 . Эта поверхность охватывает суммарный заряд
. Эта поверхность охватывает суммарный заряд 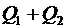 . Следовательно, для нее уравнение, записанное на основе теоремы Остроградского-Гаусса, будет иметь вид:
. Следовательно, для нее уравнение, записанное на основе теоремы Остроградского-Гаусса, будет иметь вид:
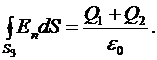
Отсюда, используя положения, примененные в первых двух случаях, найдем:
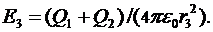 (4)
(4)
Убедимся в том, что правые части равенств (3) и (4) дают единицу напряженности электрического поля:
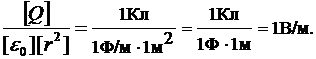
Выразим все величины в единицах CИ ( 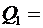 10-9Кл,
10-9Кл, 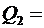 -0,5∙10-9Кл,
-0,5∙10-9Кл, 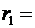 0,09м,
0,09м, 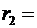 0,15м, 1/(4
0,15м, 1/(4 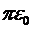 )=9∙109м/Ф).
)=9∙109м/Ф).
Произведем вычисления:
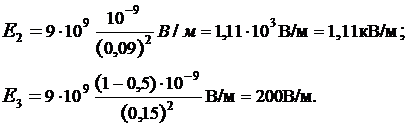
4. Построим график 
В области I ( 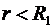 ) напряженность
) напряженность 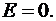
В области II ( 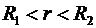 ) напряженность
) напряженность 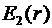 изменяется по закону:
изменяется по закону: 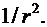
В точке 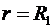 напряженность
напряженность 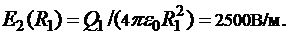
В точке 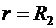 (
( 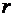
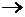
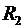 слева)
слева) 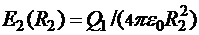 ,
, 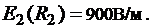
В области III ( 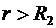 )
) 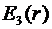 изменяется по закону:
изменяется по закону: 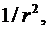 причем в точке
причем в точке 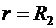 (
( 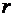
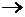
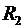 справа):
справа):
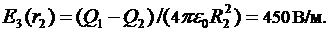
Таким образом, функция 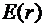 в точках
в точках 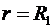 и
и 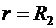 терпит разрыв.
терпит разрыв.
График зависимости 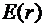 представлен ниже.
представлен ниже.
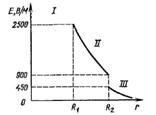
Ответ: 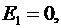
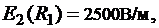
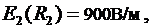
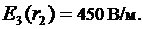
Задача 5.
 Два одинаковых положительных заряда расположены на расстоянии r друг от друга в однородной среде с диэлектрической проницаемостью
Два одинаковых положительных заряда расположены на расстоянии r друг от друга в однородной среде с диэлектрической проницаемостью 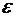 . Найти потенциал в точке, расположенной на одинаковом расстоянии
. Найти потенциал в точке, расположенной на одинаковом расстоянии 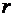 как от одного, так и от другого заряда.
как от одного, так и от другого заряда.
Решение.
|
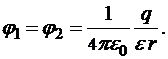
Отсюда:
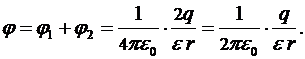
Ответ: 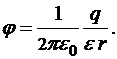
Задача 6.
Электрическое поле создано длинным цилиндром радиусом 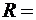 1см, равномерно заряженным с линейной плотностью
1см, равномерно заряженным с линейной плотностью 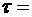 20нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстояниях
20нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстояниях 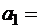 0,5см и
0,5см и 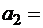 2см от поверхности цилиндра в средней его части.
2см от поверхности цилиндра в средней его части.
Решение.
Определим разность потенциалов, используя соотношение между напряженностью поля и изменением потенциала: 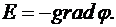 Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде:
Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде:
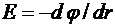 или
или 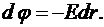 (*)
(*)
Интегрируя выражение (*), найдём разность потенциалов двух точек, отстоящих на расстояниях 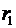 и
и 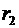 от оси цилиндра:
от оси цилиндра:
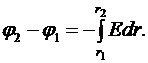 (**)
(**)
Для напряженности поля воспользуемся формулой:
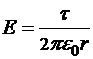 (***),
(***),
т.к. цилиндр длинный и точки взяты вблизи его средней части.
Подставив (***) в выражение (**), получим:
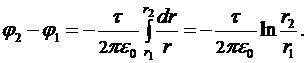 (1)
(1)
Величины 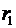 и
и 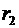 входят в формулу в виде отношения, то их можно выразить в любых, но только одинаковых единицах:
входят в формулу в виде отношения, то их можно выразить в любых, но только одинаковых единицах:
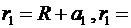 1,5см и
1,5см и 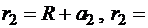 3см.
3см.
Подставив значения величин в формулу (1), получаем:
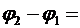 250В.
250В.
Ответ: 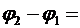 250В.
250В.
Задача 7.
Положительные заряды Q1=3мкКл и Q2=20нКл находятся на расстоянии 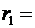 1,5м друг от друга. Определить работу А, которую надо совершить, чтобы сблизить заряды до расстояния r2 =1м.
1,5м друг от друга. Определить работу А, которую надо совершить, чтобы сблизить заряды до расстояния r2 =1м.
Решение.
Положим, что Q1 остается неподвижным, а Q2 – движется. Работа внешней силы:
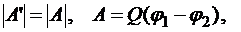
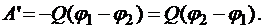
Потенциалы точек начала и конца пути:
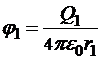 и
и 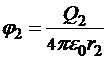
учтя, что Q=Q2 , получим:
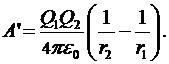
Учитывая, что 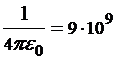 м/Ф, после подстановки числовых значений и вычислений, получаем:
м/Ф, после подстановки числовых значений и вычислений, получаем:
А=180мкДж.
Ответ:А=180мкДж.
Домашнее задание:
[Л-2] – 9.1, 9.5, 9.9, 9.10, 9.23, 9.32, 9.46, 9.52;
[Л-3] – 3.4, 3.6, 3.8, 3.15;
[Л-4] – 3.2, 3.12, 3.20, 3.24, 3.34, 3.43.
Дата добавления: 2018-04-15; просмотров: 345; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

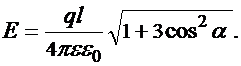
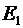 в области I проведем сферическую поверхность
в области I проведем сферическую поверхность 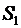 радиусом
радиусом 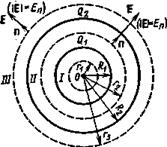
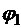 и
и 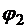 , созданных каждым из зарядов.
, созданных каждым из зарядов.