Разностные формулы для аппроксимации первой и второй производных.
Составил: ст. преп. Мартынова Т.Е., компьютерная вёрстка: ст. преп. Мартынова Т.Е. ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Памятка по ключевым вопросам теории для подготовки к экзамену.
Определение абсолютной и относительной погрешности.
Пусть y – точное неизвестное значение некоторой величины, а y* – ее известное приближенное значение. Разность 
между точным и приближенным значением величины принято называть ошибкой, а меру ошибки – погрешностью.
Абсолютная погрешность – это количественная мера ошибки, вычисляемая по формуле:
. (1.1)
Относительная погрешность – это качественная мера ошибки, представляющая собой долю ошибки в значении y:
. (1.2)
Непосредственное вычисление погрешностей по формулам (1.1) и (1.2) невозможно (как правило, 
неизвестно), поэтому для оценки абсолютной погрешности задают верхнюю границу:
, (1.3)
а для относительной погрешности полагают :
. (1.4)
Оценка абсолютной погрешности функции нескольких переменных.
Пусть 
– функция одной переменной, для которой известна абсолютная погрешность 
. Тогда абсолютная погрешность значения функции в точке 
оценивается по формуле
. (2.1)
Если функция зависит от нескольких переменных 
, то формула для оценки абсолютной погрешности принимает вид:
|
|
|
. (2.2)
Постановка задачи интерполяции.
Пусть функция задана набором значений в 
точках (т.е. таблично): 
.
Значения аргумента 
, представленные в таблице, называются узлами интерполяции. Требуется построить приближающую функцию 
, которая будет точно проходить через узловые значения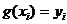 
, а между ними будет достаточно близкой к 
, т.е. 
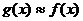вне .
Пример графической иллюстрации постановки задачи интерполяции представлен ниже на рисунке.
Определение сплайна и его дефекта.
Пусть отрезок 
разбит точками 
на 
частичных отрезков 
. Сплайном степени m называется функция 
, обладающая следующими свойствами:
1) функция непрерывна на отрезке вместе со своими производными 
до некоторого порядка 
;
2) на каждом частичном отрезке функция совпадает с некоторым алгебраическим многочленом 
степени m, : 
.
Дефектом сплайна называется разность 
между степенью сплайна 
и наивысшим порядком его производной, непрерывной на отрезке .
Идея метода наименьших квадратов.
В вычислительной математике метод наименьших квадратов применяется для аппроксимации таблично заданной функции . В отличие от интерполяции, не требуют точного прохождения приближающей функции 
через заданные точки таблицы. Приближающую функцию ищут в виде обобщенного многочлена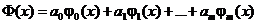 
, где 
− заданные базисные функции, 
− неизвестные коэффициенты, подлежащие определению. Ясно, что можно построить множество функций, удовлетворяющих условию 
. Критерием выбора наилучшей аппроксимирующей функции является минимум среднеквадратического отклонения 
. Набор базисных функций подбирают из свойств исходных данных, он должен быть линейно независимым и, по возможности, иметь небольшой объем ( 
). Задача заключается в нахождении неизвестных коэффициентов при условии 
. Необходимым условием минимума функции нескольких переменных (в данном случае 
переменная) является равенство нулю ее частных производных по всем независимым переменным. Это условие дает систему линейных алгебраических уравнений 
,
|
|
|
которая носит название нормальной системы метода наименьших квадратов. Поскольку основная матрица системы является симметрической и положительно определенной, решение системы доставляет минимум 
.
Наиболее часто используют полиномиальный базис 
для 
. В простейшем случае для 
имеем линейный многочлен наилучшего среднеквадратического приближения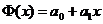 
. СЛАУ для определения коэффициентов 
и 
принимает вид: 
|
|
|
. На рисунке приведен пример линейной аппроксимации: 
Разностные формулы для аппроксимации первой и второй производных.
Пусть функция задана набором значений в (n+1)-ой точке 
, причём узлы расположены по возрастанию и через один и тот же интервал:
; 
.
Формулы
, 
, 
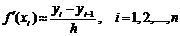есть правая, левая и центральная разностные производные первого порядка соответственно.
Центральная разностная производная второго порядка
.
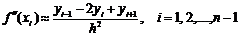Правая и левая разностные производные имеют первый порядок точности по 
, а центральные – второй.
Дата добавления: 2018-04-15; просмотров: 310; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!