ЦВ параллельного кодирования.

ИН- источник опорных напряжении, вырабатывает напряжение U_k1, U_k2… U_kN; ОУ- отсчетное устройство; ПКК- преобразователь единичного кода в код; СУ1…СУ_N – сравнивающие устройства

В данном вольтметре измерение напряжения происходит путем сравнения его сразу со многими эталонами, кот вырабатывает источник опорных напряжений - ИН, что требует такого же количества сравнивающих устройств, как и эталонов.

Преимущество метода преобразования: высокое быстродействием.

Недостатки - требует большое кол-во сравнивающих устройств и сложность источника опорного напр-я.

 

Погрешность ЦИП. Основные состовляющие.

Основная погрешность ЦИП складывается из 4-х составляющих:

а) погрешность дискретизации Δx_д ;

б) погрешность реализации уровней Δx_p квантования, возникающая из-за того, что измеряемая величина квантуется в соответствии с реальными значениями уровней, а отсчет производится в соответствии с принятыми значениями;

в) погрешность от наличия порога чувствительности СУ Δx_ч, возникающая в результате сравнения неизвестной величины с известной;

г) погрешность Δx_п, возникающая вследствие действия помех.

Погрешности Δx_р, Δx_ч Δx_п обусловлены несовершенством узлов ЦИП и поэтому их называют составляющими инструментальной погрешности. Погрешность дискретизации – методическая погрешность.

Погрешность дискретизации. Погрешность реализации уровней.

Погрешность дискретизации будет зависеть от способа отождествления уровня квантования. Рассмотрим случай последовательного счета, в котором величина x сравнивается с известной величиной х_к, которая изменяется во времени скачками в 1 квант. Определение отождествляемого уровня происходит при установлении равенства х = х_к или точнее при выполнении условия: х_к>x .

Вых сигнал должен выставляться в соответствии с отождествляемым уровнем.

Положим, что отождествление неизвестной величины х происходит с ближайшим большим или равным уровнем квантования, т.е. в данном случае с уровнем х_кi. Следовательно, в момент времени t₂  установится соотношение 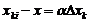, где α - коэф в пределах от 0 до 1.

Поскольку α зависит от измеряемой величины х, кот является случайной величиной, то погрешность дискретизации имеет также случайный характер.

Закон распределения зависит от з-на распределения х. Однако вследствие практически равной вероятности появления размеры величины в пределах одного кванта Δх_к з-н распределения принимают равновероятным. При этом з-не распределения дисперсия погрешности, мат ожидание и средн значение: ; ; .

Представление характера изменения погрешности при отождествлении с ближайшим большим значением изображено на рис

При отождествлении неизвестн величины х с ближайшим уровнем квантования вследствие равной вер-ти появления значений х в пределах 1го кванта погрешность Δх_д м.находиться в пределах 0…∆хк. В данном случае погрешность нах-ся в диап-не [ 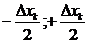]. При этом мат ожидание и дисперсия=0.

---

Дата добавления: 2018-04-15; просмотров: 301; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!