Расчет оптимальных настроек ПИ регулятора для одноконтурной системы методом расширенных АФЧХ.

⇐ ПредыдущаяСтр 4 из 5Следующая ⇒

Из теории: 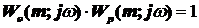, где m – степень колебательности, а ψ – коэффициент затухания:

Расчет производится посредством выделения вещественной и мнимой части РАФЧХ.

Алгоритм расчета следующий:

1. Подставляя в передаточную функцию объекта и регулятора вместо , получим РАФЧХ объекта и , соответственно.

2. Из теории запишем:

3. , , где:

4. Решается система относительно и .

5. Строится график зависимости , где .

Передаточная функция ПИ регулятора описывается выражением:

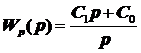где C₁ и C₀ соответствуют пропорциональному и интегральному коэффициентам регулятора. Подставляя вместо оператора Лапласа значения , получим выражение РАФХ для ПИ регулятора:

Аналогичную подстановку сделаем и для передаточной функции объекта:

1-ого порядка:

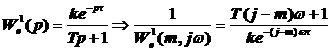
2-ого порядка:

Полученные выражения подставляем в (1). Выделяем действительную и мнимую части и решаем систему уравнений относительно и , подставляя численные значения , , , и выбранную степень колебательности m.

В общем случае для объекта 1(2)-ого порядка C₁ и C₀ имеют вид:

или

Далее, задача сводится к построению графика линии равной степени затухания, т.е. зависимости , где . График строится до тех пор, пока первый раз не пересечет ось абсцисс, т.е. пока . Определяем координаты точки, соответствующие максимальному значению . Следующая за ней точка с координатами по ω и будет соответствовать оптимальным параметрам ПИ регулятора.

********************************************************

(В тексте отчета привести краткое описание программы)

********************************************************

График линии равной степени затухания представлен на рис. 5.

В результате вычислений получим, что при изменении частоты от ___ с шагом ___, максимум функции 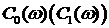будет в точке ___, а координаты, соответствующие оптимальным параметрам ПИ регулятора имеют значения: .

Т.о. передаточная функция ПИ регулятора с оптимальными настройками имеет вид:

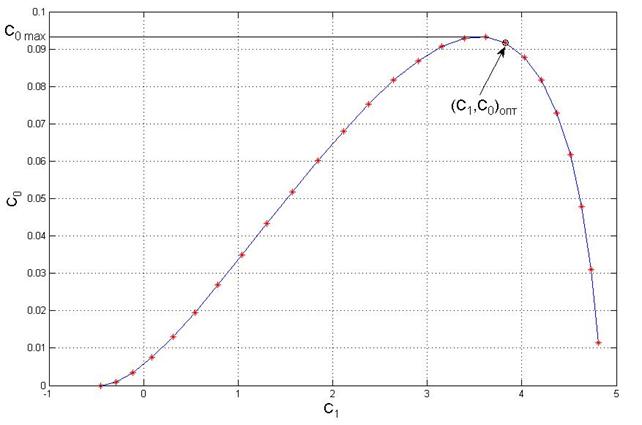
Рис. 5. Линия равной степени затухания

Устойчивость АСР по критерию Михайлова

Критерии, использующие характеристическое уравнение

Из достаточно большого множествакритериев устойчивости систем управления модно выделить группу критериев, которые основаны на использовании характеристического уравнение системы управления. К таким критериям относятся критерий Рауса-Гурвица и критерий Михайлова.

Характеристического уравнение системы управления получают путем приравнивания 0 знаменателя передаточной функции системы:

где , .

В системе MATLAB помощью функции feedback можно получить передаточную функцию замкнутого контура системы управления. Отмерим, что ПФ объекта в данном случае задается без множителя запаздывания. Командой:

[num,den]=tfdata(sysAll,'v');

получим вектор коэффициентов знаменателя. Параметр 'v' предназначен для того, чтобы получить коэффициенты в виде вектора, а не ячеек с содержанием вектора. Эти коэффициенты соответствуют коэффициентам характеристического уравнения системы.

Критерий Рауса-Гурвица

Из теории известно, что критерий сводится к составлению определителя Гурвица и определению положительности соответствующих миноров. Для АСР 1-ого и 2-ого порядка с ПИ регулятором (как в прямом контуре, так и в контуре обратной связи) характеристическое уравнение будет иметь вид:

а их определители:

Если поставить коэф-ты в соответствии с записью векторов в MATLAB, то к соответствующему индексу надо прибавить 1.

М.б. два варианта решения проблемы:

1. Из коэф-тов вектора составляется определитель в виде квадратной матрицы и вычисляются определители всех диагональных алгебраических дополнений, путем пошагового удаления последней строки и последнего столбца. Все они должны быть больше 0 (положительны).

Длина вектора определяется функцией length(Nvec), а определитель вычисляется финкцией det(mat).

2. Прямое сравнение коэффициентовтов. Для системы 1-ого порядка:

Для системы 2-ого порядка:

В результате получаем, что:

или

Откуда можно сделать вывод, что система управления устойчива.

Критерий Михайлова

Для того чтобы система была устойчива, необходимо и достаточно, чтобы при ее кривая Михайлова, начинаясь с положительной вещественной полуплоскости, последовательно обходила квадрантов в положительном направлении (против часовой стрелки). Следует отметить, что кривые Михайлова устойчивых систем не пересекают начало координат и уходят на в -ом квадранте.

Для использования этого критерия в характеристическом уравнении оператор Лапласа заменяется на , Вследствие чего получим уравнение годографа Михайлова:

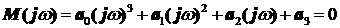Замена оператора Лапласа в системе MATLAB осуществляется с помощью цикла for.

Выделяя вещественную и мнимую части функциями real и imag, строим годограф Михайлова в координатах . Далее по графику считаем количество пересеченных квадрантов.

График, соответствующий критерию Михайлова приведен на рис. 6

В результате из графика видно, что годограф Михайлова пересекает 2(3) квадранта. Т.к. порядок характеристического уравнения системы для объекта 1(2) порядка равен 2(3), следовательно, согласно критерию михайлова мохно заключить, что система устолйчива.

Рисунок 6. Годограф Михайлова

Критерий Найквиста

Критерий можно записать так: если кривая АФЧХ разомкнутой АСР не охватывает точку (–1; j0), то замкнутая АСР является устойчивой.

Поэтому, строим диаграмму Найквиста для системы с помощью функции Nyquist:

Nyquist(sysR*sysO), grid on

Диаграмма Найквиста представлена на рис. 7.

Из графика очевидно, что кривая не охватывает точку (–1; j0), сто соответствует устойчивости системы.

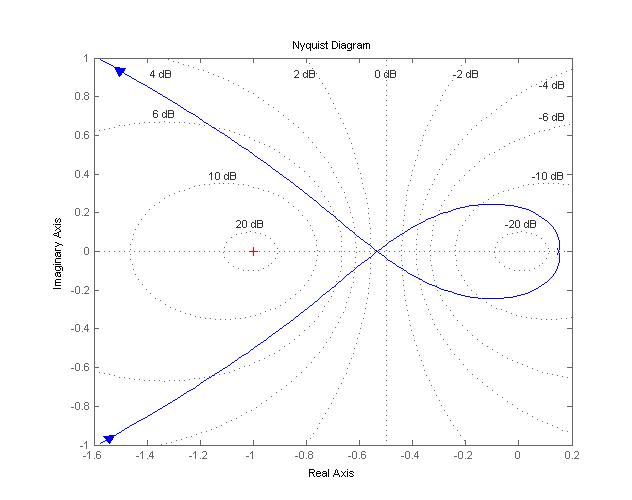
Рис. 7. Диаграмма Найквиста

Дата добавления: 2018-04-15; просмотров: 519; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 Следующая ⇒

Мы поможем в написании ваших работ!