Решение задачи корреляционно-регрессионного анализа в интегрированных системах
На основе приведенных в табл. 3 данных необходимо:
n сформулировать экономическую постановку задачи;
n провести логический и графический анализ исходных данных и построить эмпирическую линию регрессию;
n рассчитать коэффициент корреляции;
n провести подбор уравнения регрессии и определить параметры;
n построить теоретическую линию регрессии;
n рассчитать ошибку уравнения регрессии, теоретическое корреляционное отношение;
n осуществить прогноз результативного признака по значению указанного фактора для найденного уравнения
Таблица 3
Даны выборочные значения (x,y):
| x | 0.2 | 1.3 | 1.7 | 2.5 | 2.8 | 3.6 | 4.1 | 5.2 | 5.4 |
| y | 1.1 | 2 | 1.9 | 2.1 | 2.3 | 2.5 | 3.1 | 3.2 | 3.7 |
| №п\п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Рассмотрим технологию решения задачи в интегрированной системе Excel.
В системе Excel расчет параметров регрессии выполняется при вызове команды /Сервис/Математика/Регрессия, которая открывает окно для задания условий расчета:
· /Независимые -задает координаты столбца или блока столбцов, в которых введены значения независимых переменных;
· /Зависимая - задает столбец со значениями зависимой величины;
· /Блок вывода - задает адрес блока, в который будут выведены результаты регрессионного анализа;
· /Начало координат - выбор в дополнительном окошке варианта расчета уравнения регрессии с константой B (альтернатива НЕТ - линия регрессии не проходит через начало координат) или без нее (альтернатива ДА);
|
|
|
· /Выполнить - инициализация расчета параметров регрессии;
· /Отменить - команда, отменяющая все заданные установки;
· /Выход- возврат в электронную таблицу.
Рассмотрим пример расчета параметров регрессии для двух показателей X и Y. Данные по задаче и отчет по решению приведены на рис. 1.
Р и с. 1. Пример расчета параметров регрессии для двух показателей X и Y (B не равно 0)
Для расчета параметров регрессии необходимо выполнить:
1. Ввести исходные данные, т. е. ряды независимых и зависимой переменных. Каждый ряд последовательно вводится в клетки одного столбца. Если независимых переменных несколько, то они обязательно вводятся в соседние столбцы. Зависимая переменная может быть введена в любой столбец.
2. Активизировать пункт меню /Сервис/Математика/Регрессия, который открывает окно задания условий расчета.
3. Выбрать пункт меню /Независимые и задать координаты блока, содержащего значения независимых переменных. В примере на рис. 1. это блок A3..A11.
4. Выбрать пункт меню /Зависимые и указать координаты блока, содержащего значения зависимой переменной (на рис. 1 - блок B3..B11).
|
|
|
5. Выбрать пункт меню /Блок вывода и задать координаты блока, в который будут выведены результаты регрессионного анализа (на рис. 1 - блок D1..G9). В этом пункте меню достаточно задать координаты верхнего левого угла блока.
6. Выбрать пункт меню /Начало координат и задать вид линии регрессии:
· Нет- линия регрессии не проходит через начало координат, а постоянный член B не равен 0 (см. рис.1.);
· Да- линия регрессии проходит через начало координат, а постоянный член B равен 0.
По умолчанию действует установка НЕТ.
7. Инициировать расчет параметров регрессии с помощью меню /Выполнить, после чего результаты регрессионного анализа автоматически помещаются в блок вывода.
Результаты регрессионного анализа в системе можно интерпретировать в графическом виде. Построим график регрессии для данных, приведенных в табл.1. Для этого в окне меню /График нужно установить следующие настройки:
* /Тип Графика - выбрать X-Y график;
* /Определить Серии: X-серия- блок A3..A11;
1-я серия- блок B3..B11;
* /Настроить Серии/Формат - указать вид вывода "Маркер".
При нажатии клавиши F10 на экран выводится график (рис.2). На нем в виде отдельных точек-маркеров указаны исходные экспериментальные данные.
|
|
|
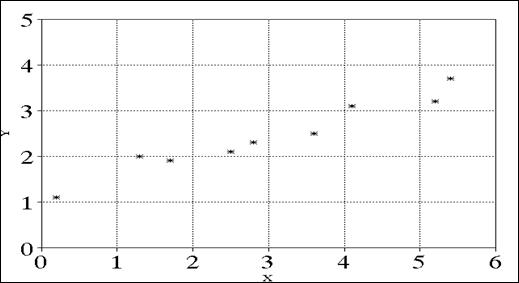
Р и с. 2. График эмпирической регрессии
Для построения линии регрессии необходимо построить в любом столбце (например в столбце H) блок вспомогательных данных, соответствующих выбранному виду уравнения регрессии Y = A*X + B или Y = A*X. Формулы в клетках вспомогательного блока будут иметь следующий вид (табл.4):
Таблица 4
Содержимое вспомогательного блока
| Адрес ячейки | Формула вычислений |
| H3 H4 ... H11 | +F$8*A3+$G$2 +F$8*A3+G$2 ... +F$8*A11+G$2 |
Затем в меню /График/Определить Серии для серии 2 (2-я серия) следует определить блок H3..H11, а в меню /Настроить Серии/Формат указать вид вывода "Линии". После этого нажатием клавиши F10 на экран выведется график с экспериментальными точками и линией регрессии (рис.3).
При анализе результатов регрессионной модели следует учитывать то обстоятельство, что терминология в ЭТ не совсем соответствует терминологии, используемой в отечественных учебниках по статистическим методам:
|
|
|
* вместо общепринятого значения коэффициента корреляции R выводится значение R-квадрат, поэтому для получения нормального значения R следует использовать формулу @SQRT(G4);
* значение "Стандартное отклонение Y" (СТО) на самом деле означает ошибку отклонения от регрессии, используемую для ограничения доверительной зоны линии регрессии (в интервале СТО укладывается 68 % всех экспериментальных данных, 2СТО - 95 %). На графике (рис.4) эти интервалы изображены штрих-пунктирной и пунктирной линиями.
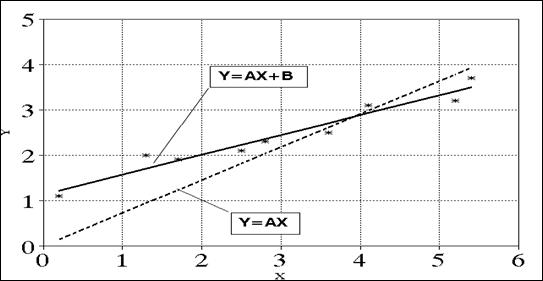
Р и с.3. График с экспериментальными точками и линией регрессии
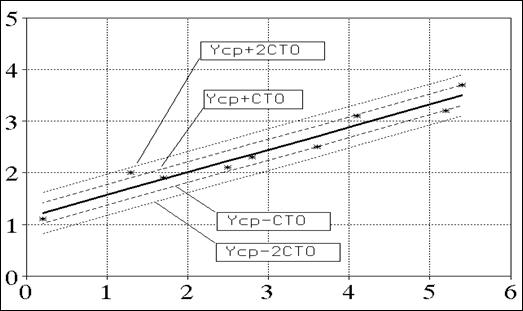
Р и с. 4. Доверительная зона линии регрессии
К сожалению, формируемая в системе таблица регрессии имеет один существенный недостаток. Она не дает оценки достоверности результатов регрессионного анализа, которая считается необходимой в любых современных методиках обработки экспериментальных данных. Для устранения этого недостатка можно путем несложных вычислений добавить в таблицу проверку достоверности по любой известной методике (например, по t-критерию Стьюдента) на основе уже имеющихся в таблице результатов. Для примера (табл.1) можно дополнительно вычислить коэффициент корреляции R, ошибку коэффициента корреляции Sr и фактическое значение критерия достоверности Стьюдента tf  по формулам:
по формулам:
R = @SQRT(G4),
Sr = @SQRT((1-G4)/G6),
tf = @SQRT(G4×G6/(1-G4)).
Эти формулы можно поместить в любые свободные клетки таблицы. Затем по таблице значений критерия Стьюдента для числа степеней свободы указанного в клетке G6, можно найти его теоретическое значение и определить уровень достоверности коэффициента корреляции R.
Варианты заданий
| Вариант 1. | Вариант 2. | ||||||
| п/п | Кол-во изделий | Отказ оборудования, % | п/п | Кол-во заболеваний | Охват профилак- тикой ,% | ||
| 1 | 10 | 25 | 1 | 5 | 60 | ||
| 2 | 20 | 20 | 2 | 10 | 50 | ||
| 3 | 30 | 15 | 3 | 12 | 40 | ||
| 4 | 50 | 10 | 4 | 18 | 30 | ||
| 5 | 40 | 5 | 5 | 15 | 20 | ||
| ? | 30 | ? | 10 | ||||
| Вариант 3. | Вариант 4. | ||||||
| п/п | Прибыль тыс руб | Износ оборудования % | п/п | Качество продукции % | Импортное сырье % | ||
| 1 | 25 | 80 | 1 | 40 | 20 | ||
| 2 | 20 | 85 | 2 | 30 | 14 | ||
| 3 | 18 | 82 | 3 | 25 | 10 | ||
| 4 | 10 | 90 | 4 | 15 | 12 | ||
| 5 | 15 | 95 | 5 | 10 | 8 | ||
| ? | 92 | ? | 30 | ||||
| Вариант 5. | Вариант 6. | ||||||
| п/п | Урожайность зерновых ц/га | Кол-во минер. удобрений ц/га | п/п | Урожайность зерновых ц/га | Кол-во минер. удобрений ц /га | ||
| 1 | 14 | 0.3 | 1 | 15 | 0.4 | ||
| 2 | 16 | 0.5 | 2 | 12 | 0.2 | ||
| 3 | 15 | 0.4 | 3 | 14 | 0.5 | ||
| 4 | 20 | 0.8 | 4 | 15 | 0.6 | ||
| 5 | 18 | 0.6 | 5 | 18 | 0.5 | ||
| ? | 0.7 | 0.7 | |||||
| Вариант 7. | Вариант 8. | ||||||
| п/п | Производство изделий | Работа второй смены % | п/п | Валов. Произв. Молока т | Доля молока населения % | ||
| 1 | 10 | 5 | 1 | 20 | 70 | ||
| 2 | 20 | 15 | 2 | 25 | 80 | ||
| 3 | 25 | 10 | 3 | 18 | 60 | ||
| 4 | 35 | 20 | 4 | 30 | 90 | ||
| 5 | 30 | 25 | 5 | 10 | 50 | ||
| ? | 35 | ? | 85 | ||||
| Вариант 9. | Вариант 10. | ||||||
| П/п | Перевозка пассажиров тыс чел | Качество обслуживания % | п/п | Прибыль предприятия тыс.руб. | Объем используемых основных средств% | ||
| 1 | 40 | 60 | 1 | 10 | 12 | ||
| 2 | 50 | 70 | 2 | 7 | 15 | ||
| 3 | 30 | 50 | 3 | 5 | 16 | ||
| 4 | 20 | 40 | 4 | 12 | 10 | ||
| 5 | 25 | 45 | 5 | 15 | 8 | ||
| ? | 80 | ? | 5 | ||||
Дата добавления: 2018-04-15; просмотров: 148; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
