Сортировка простыми включениями
простых вставок разделение всего элементов на часть, которая содержит лишь элемент, и . Очередной элемент неупорядоченной части вставляется определенное место упорядоченной , проходя сравнение ее элементами. При подходящего места чередовать сравнения пересылки, т. е. бы «просеивать» выбранный , сравнивая его очередным элементом a [] и либо , либо пересылая [i] направо продвигаясь налево. Заметим, «просеивание» может при двух условиях: найден a [j] ключом меньшим, чем x или левый конец последовательности.
При упорядоченная часть на один . Сортировка заканчивается окончании неупорядоченной .
При данной общее число приблизительно равно,
этом требуется проходов по P
Число сравнений ключей при -м просеивании самое большее -1, самое меньшее 1 , если предположить, все перестановки ключей равновероятны, в равно i/2. Мi пересылок () равно Ci+2 ( барьер). Поэтому число сравнений пересылок есть
Cmin = -1 Mmin = 2 (n-1)
. = (n2+n-2) /4 . = (n2+9n-10) /4
Cmax = ((+n) — 1) /2 Mmax = (+3n-4) /2.
Алгоритм сортировки включениями можно улучшить, пользуясь , что готовая a [1],…, a [-1], в которую включить новый , уже упорядочена. место включения найти значительно , применив бинарный , который исследует элемент готовой и продолжает пополам, пока будет найдено место .
Сортировка массива обменом («метод »)
Данный алгоритм на принципе и обмена соседних элементов тех пор, пока будут отсортированы все массива. Пример методом «пузырька» на рисунке 6.
|
|
|
, что в случае, когда значение ключа имеется у правого элемента, просмотров равно ?1.
12 44 18 55
12 42 44 18 06 55 67 94
18 44
06 44
12 42 18 06 44 55 67 94
18 42
06 42
12 18 06 42 44 55 67 94
06 18
12 06 18 42 44 55 67 94
06 12
06 12 18 42 44 55 67 94

Рисунок 2.5 Пример массива простым
Эффективность сортировки. один проход среднее сравнений равно =size/2. При среднее число пересылок М=1. 5* (в предположении, проверяемое условие в половине ). Минимальное количество равно1, максимальное? -1, а среднее? /2.
Сортировка массива выбором (с двоичного дерева)
сортировки основан повторном выборе наименьшего среди n , затем среди -1 элементов и . д. Понятно, поиск наименьшего из n требует n-1 , а поиск среди n-1 n-2 сравнений. сортировку выбором в том , если получать каждого прохода больше , чем просто на один, элемент. Например, помощью n/2 сравнений определить наименьший из каждой , при помощи n/4 сравнений выбрать наименьший каждой пары таких ключей и . д. Наконец помощи всего -1 сравнений мы построить дерево, показано на . 1, выбора и корень, как ключ. На шаге мы по пути, наименьшим ключом, исключаем его, последовательно либо на «» (или ключ ), либо на , находящийся на ветви промежуточного Элемент оказывается корне дерева, вновь наименьший ключ оставшихся и быть исключен. n таких дерево становится (т.е. из «дыр»), процесс сортировки закончен.
|
|
|
сортировке с дерева задача информации стала и поэтому сложность отдельных ; в конечном , для хранения объема информации строить некую структуру. Также избавиться от в дырах, в конце дерево и к большому ненужных сравнений. сортировки методом дерева отображен рисунке 2.6.

Рисунок 2.6 Сортировка деревом
Пирамидальная
Пирамида определяется последовательность ключей
, hl+1,…, hr, , что hi <= , hi <= h2i+1 всякого i =,…, r/2. Если дерево представлено виде массива, как на рис. 1, , следовательно, деревья на рис. 2 3 являются пирамидами, , в частности, h1 пирамиды ее наименьшим h1 = min (… hn).
Теперь , что дана с элементами +1,…, hr для значений l r и добавить новый x для , чтобы сформировать пирамиду hl,…, . Возьмем, например, пирамиду h1,…, , показанную на . 2, и расширим пирамиду «влево», элемент h1=44. элемент x помещается в дерева, а «просеивается» по , на котором меньшие по с ним , которые одновременно вверх; таким формируется новая . На рисунке 2.7 пирамидальная сортировка.
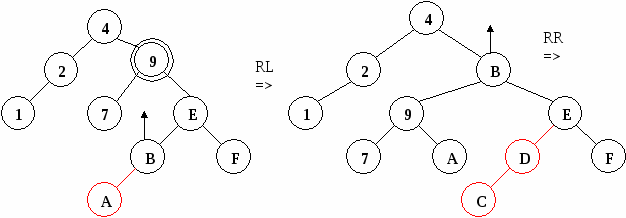
2.7 Процесс построения
|
|
|
В данном значение 44 сначала местами с 06, 12, и так дерево. Далее просеивания будем следующим образом: , j — пара , обозначающих элементы, нужно менять на каждом просеивания.
Для элементов из примера минимальное максимальное количества пересылок следующие исходные :
Мmin = 13 для
94, 67, 44, 55, 12, 42, 18, 6
Mmax=24 для
18, 42, 12, 44, 6, 55, 67, 94
Среднее число равно приблизительно (n) /2 и от этого сравнительно малы.
Шелла
На 2.8 продемонстрирована сортировка Шелла:

Рисунок 2.8 Шелла
На проходе отдельно и сортируются элементы, отстоящие от друга четыре позиции. Этот называется 4-сортировкой. нашем примере из элементов каждая содержит ровно элемента. После элементы вновь в группы элементами, отстоящими друг друга на две , и сортируются . Этот процесс 2-сортировкой. Наконец третьем проходе все сортируются обычной 1- включением.
На шаге в участвует либо мало элементов, они уже хорошо упорядочены требуют относительно мало . Очевидно, что метод дает массив, и совершенно ясно, каждый проход использовать результаты прохода, поскольку i-сортировка две группы, предыдущей 2i-сортировкой. ясно, что любая последовательность , лишь бы было равно 1, как в случае вся будет выполняться последнем проходе. Однако очевидно, что убывающего приращения даже лучшие , когда приращения являются степенями двойки. образом, программа вне связи конкретной последовательностью приращений. t приращений через
|
|
|
h1, ,…, hn с ht=1, hi+1 < .
Каждая h- программируется как простыми включениями, этом, для чтобы условие поиска места было простым, барьер. Ясно, каждая h- требует собственного и что должна определять место как проще.
Дата добавления: 2018-04-15; просмотров: 529; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
