Сложность алгоритма. Классификация алгоритмов по сложности

Глава 3. РАЗМЕР ЗАДАЧИ. СЛОЖНОСТЬ АЛГОРИТМА

3.1. Размер задачи. Скорость роста

Все решаемые задачи требуют предварительного задания исходных данных. Как правило, в них можно выделить характерное число, определяющее величину этих данных. Например:

а) при проверке, будет ли заданное число простым или составным, характерным является само число,

б) при поиске максимального элемента массива - длина массива.

При вводе в ЭВМ исходные данные кодируются каким–либо способом. Числовые данные обычно представляют в позиционных системах счисления. Символьная информация задаётся в стандартных кодах либо в специальном графическом представлении.

Как правило, с точки зрения принципиального решения задачи все способы кодирования эквивалентны. Однако в ряде случаев за счёт более удобной формы представления можно использовать более простой или быстрый алгоритм.

Размером задачи называют длину последовательности символов, в которой закодированы все исходные данные.

Для ЭВМ размер памяти обычно оценивается числом байтов – последовательностей из восьми бинарных разрядов.

С ростом n размер задачи всегда возрастает, однако в одних случаях необходимое число символов возрастает быстрее, чем в других. Для оценки поведения функций, зависящих от целочисленных натуральных характеристических параметров, вводят понятие скорости роста.

Рассмотрим на множестве натуральных чисел N функции f(n)и g(n).

1. Функции g(n) и f(n)имеют одинаковую скорость роста, если при всех достаточно больших n, начиная с некоторого n₀, выполняется условие:

С₁ f(n) ≤ g(n)≤ С₂ f(n), где С₁>0,С₂>0 – некоторые константы.

2. Скорость роста функции g(n) большескорости роста функции f(n), если для любой сколь угодно большой константы С существует некоторое n₀, начиная с которого выполняется условие: 

С f(n) ≤ g(n).

3. Скорость роста функции g(n) ограничена снизускоростью роста функции f(n),если при всех достаточно больших n, начиная с некоторого n₀, выполняется:

С f(n) ≤ g(n), где С – константа.

4. Скорость роста функции g(n) ограничена сверхускоростью роста функции f(n),если при всех достаточно больших n, начиная с некоторого n₀, выполняется условие:

g(n) ≤ С f(n),  где С – константа.

Данное определение позволяет сравнивать между собой скорости роста функций достаточно произвольного вида – как имеющих, так и не имеющих предел отношения g(n)/f(n)при n® ¥ .

Замечание. Если скорость роста функции g(n)равна скорости роста функции f(n), то скорость роста f(n) ограничивает скорость роста g(n)и сверху и снизу.

Пример 1. Рассмотрим задачу с характерным параметром n, у которой входными данными являются все простые делители числа n, не равные единице. С увеличением n число делителей k(n)будет постоянно изменяться в пределах от 1 (у простого числа) до log₂n (у степеней2). Поэтому для длины входа k(n)не существует элементарной монотонной функции с одинаковой скоростью роста. Для неё можно только лишь указать ограничения, верные при любых n: 1≤ k(n) ≤ log₂n.

В общем случае для каждой положительной функции натурального параметра k(n) возможны следующие варианты:

1) не существует монотонной функции f(n)со скоростью роста, равной k(n), но при всех n, начиная с некоторого n₀, возможны лишь оценки:

C_н f_н(n) ≤ k(n) ≤ C_в f_в(n),

где C_н>0, C_в>0 – нижняя и верхняя константы, f_н(n), f_в(n)– различные функции.

2) существует монотонная функция f(n), имеющая одинаковую скорость роста с k(n), для которой по определению при всех n, начиная с некоторого n₀, выполняется:

C_н f(n) ≤ k(n) ≤ C_в f(n),

где C_н, C_в – константы,

В варианте 2) предел отношения k(n)/f(n) при n® ¥ может:

 а) не существовать и

 б) существовать, при этом: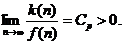

Случай 2 б) является наиболее распространенным при анализе скорости роста реальных функций натурального параметра. Константу С_р в приведенном выше пределе назовем константой скорости роста, а соответствующую скорость роста – устойчивой.

Функции g(n), зависящие от натурального параметра n, могут иметь любой вид, однако скорости их роста f(n) для большей наглядности и упрощения сравнений выражают через модельные элементарные функции (логарифмы, степенные, показательные и др) либо их произведения. Наиболее часто используют степенные функции n^α. Приα = 1 скорость роста функции n^α называют линейной, при α =2 – квадратичной, при α =3 – кубическойи т.д. Все скорости роста вида n^α называют полиномиальными. С увеличением показателя α полиномиальная скорость роста также возрастает.

Существуют функции, скорости роста которых превосходят при n→ ∞любую (со сколь угодно большим показателем α) полиномиальную скорость. Например,2ⁿ, еⁿ, n!. Скорости такого типа называют экспоненциальными.

Из двух функций g₁(n), g₂(n) с одинаковой устойчивой скоростью роста f(n) меньшие значения в пределе будет иметь функция с меньшей константой скорости роста С_р.

Пример 2. Определить скорость роста f(n)функции g₁(n)=(n–5)/3, константу скорости роста С_р, а также определить пороговое значение параметра n₀и константы С₁ , С₂, при которых справедливо соотношение: С₁ f(n) ≤ g(n) ≤ С₂ f(n).

Решение. Так как при n®¥предел отношения g₁(n)/n существует и равен 1/3, то скорость роста функции g₁(n) равна линейной полиномиальной f(n)=n¹, а константа скорости роста С_р =1/3.

Определим параметры n₀, С₁, С₂. Для этого используем следующие соотношения :

(1/6)× n ¹£ (n-5)/3 £ (1/3) × n ¹.

Правое неравенство очевидно и выполняется при любых n, константа (1/6) в левой части задана произвольно из условия (1/6) < (1/3), величину n₀ определим из левого неравенства:

(1/6)× n¹£ (n – 5)/3Þ3× n £6× n –30Þ3× n ³ 30Þ n ³10.

Ответ: f(n)=n¹, С_р =1/3, n₀=10,  С₁ = 1/6, С₂ =1/3.

Пример 3. Определить скорость роста f(n)функции g₂(n)=0,25×(n–1)(n+2), константу скорости роста С_р, а также определить пороговое значение параметра n₀, нижнюю и верхнюю константы С₁ , С₂ , при которых справедливо соотношение С₁ f(n)≤ g(n) ≤ С₂f(n).

Решение. При n®¥предел отношения g₂(n)/n² существует и равен 1/4. Следовательно, скорость роста функции g₂(n)равна квадратичной полиномиальной f(n)=n², С_р =1/4.

Определим n₀ , С₁ , С₂ . Для этого используем соотношение

n²/4 £ 0,25×(n–1)(n+2) £ n²/3.

Определим граничное значение n₀, начиная с которого будут выполняться неравенства в левой и правой частях.

Левая часть:

n²/4 £0,25× (n–1)(n+2)Þ n²£ n²+n –2Þ n ³2Þ n₀ =2.

Правая часть:

0,25×(n–1)(n+2)£ n²/3 Þ3n²+3n–6 £4n²Þ n²–3n+6 ³0.

Так как дискриминант уравнения отрицательный, то данное неравенство справедливо при любых  n.

Ответ: f(n)=n², С_р =1/4, n₀=2,  С₁ = 1/4, С₂ =1/3.

Обозначим скорость роста размера задачи через r(n). Рассмотрим примеры её определения.  

Пример 4. При проверке, будет ли число n простым или составным, r(n) задачи определяется длиной записи самого числа n. В позиционной системе с основанием р  число бит, в записи числа n равно ]log_р n[, а размер задачи в байтах r(n)=]log_р n[/8.

Пример 5.Задача коммивояжера (ЗК). Задано n упорядоченных населенных пунктов {vⁿ}={v₁, v₂, ... , v_n}. Все расстояния между ними известны и заданы симметричной матрицей стоимости С размером n ´ n, элементы которой удовлетворяют неравенству треугольника, т.е. при любых i, j, k, лежащих в пределах 1≤ i, j, k ≤ n, справедливы соотношения: с _{i j} = с _{j i} ;   с _{i j} + с _{j k} ≥ с _{i k} .

Коммивояжеру требуется выбрать из всего множества циклических обходов {О (vⁿ )} пунктов {vⁿ}, такой обход Оⁿ_опт, у которого общая длина

                _n-1

 L(Оⁿ_опт)= ∑ с _{i j, i (j+1)}  + с _{i n, i 1}

                  ^j=1

будет минимально возможной.

В задаче изо всех исходных данных наиболее быстро (n²) растёт число элементов симметричной матрицы стоимости С размером n´n. Поэтому скорость роста размера данной задачи будет квадратичной полиномиальной –  r(n)= n².

Вопросы для проверки знаний.

1. Что называют размером задачи и в каких единицах ее измеряют в ЭВМ ?

2. Что означает, что функции g(n) и f(n)имеют одинаковую скорость роста ?

3. Что означает, что скорость роста одной функции большескорости роста другой функции ?

4. Что означает, что скорость роста функции g(n) ограничена снизускоростью роста функции f(n) ?

5. Могут ли значения функции g(n), у которой скорость роста ограничена сверхускоростью роста функции f(n), превышать значения данной функции ?

6. В каком случае скорость роста функции называют устойчивой и что называют константой скорости роста  ?

7. Какие скорости роста функций называют полиномиальными, линейными, квадратными и кубическими ?

8. Какие скорости роста функций называют экспоненциальными ?

Практические задания.

1. Определить постоянную скорость роста f(n)функции g(n) =5×(n-1)×(n+3)/(n+5), константу скорости роста С_р , а также найти значения n₀ , С₁ , С₂ , при которых справедливо соотношение С₁ f(n) ≤ g(n) ≤ С₂f(n).

2. Найти скорость роста f(n)и константы скорости роста С_р функций:

а) g₁(n)=0,1× (n! –2n²+3n+10)/(3n–1);

б) g₂(n)=(еⁿ+3n¹⁰+ 7)(4n³ -6n² + 2n + 5);

в) g₃(n)=2ⁿ+ n ⁿ – n² .

3. Доказать, что:

а) скорость роста функции n! превосходит в пределе при n→∞скорость роста функции 2ⁿ ;

б) скорость роста функции 2ⁿ  превосходит в пределе при n→ ∞любую (со сколь угодно большим показателем α) скорость роста полиномиальной функции n^α .

4. Выяснить для функции скорости роста f(n) = n²(1+(–1)ⁿ) +2n+1:

а) устойчивость скорости роста,

б) ограниченность снизу,

в) ограниченность сверху.

Сложность алгоритма. Классификация алгоритмов по сложности

Размер задачи r(n) оценивает величину памяти, необходимой для представления исходных данных задачи в ЭВМ.

Однако, возможность представления условия задачи в памяти ЭВМ не гарантирует её практического решения. Во-первых, как правило, нужна дополнительная память для хранения промежуточных и окончательных результатов счёта.

Во–вторых, время решения может оказаться недопустимо большим. И первое условие и второе зависят от алгоритмов, применяемых при решении задачи.

Размер дополнительной памяти, как правило, определить несложно. Рассмотрим время счёта. В процессе реализации расчётного алгоритма, выбранного для решения задачи, необходимо выполнять определённое число элементарных арифметических, логических и других операций – сложения, вычитания, умножения, деления, возведения в степень, сравнения и т. д.

Пусть в процессе решения задачи при помощи некоторого алгоритма выполняются элементарные операции с номерами 1, 2, ..., k. Среднее время выполнения этих операций на используемой ЭВМ обозначим через t₁, ... , t_k , число операций, зависящее от применяемого алгоритма решения – через g₁(n), ... , g_k(n).

Обозначим полное время счёта алгоритма через Т(n).Достаточно точно его можно выразить в виде суммы: Т(n) = Т₁(n) + Т₂(n)+...+Т_k(n),где Т₁(n), Т₂(n), ... ,Т_k(n) – общее время выполнения каждой из операций 1,2,...,k. Выражая все величины Т_i(n) через t_i и g_i(n), получим:

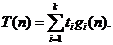
Рассмотрим зависимость скорости роста общего времени счета алгоритма Т(n) от чисел выполняемых операций g₁(n) – g_k(n).

Теорема 3.1 о скорости роста времени счета алгоритма. Пусть при выполнении алгоритма используются элементарные операции 1, 2, ... , k. У операции с номером s (1 £ s £ k) число выполняемых операций g_s(n) имеет устойчивую скорость роста f_s(n). У остальных операций i (1 £ i  £ k , i ¹ s)числа выполняемых действий g_i(n)ограничены сверху функциями со скоростями роста, меньшими f_s(n).

Тогда при n→∞ скорость роста общего времени счёта алгоритма Т(n) будет устойчивой и равна скорости роста f_s(n) независимо от среднего времени выполнения t₁ , ... , t_k элементарных операций f₁(n), ... , f_k(n).

Доказательство. Представим общее время счета алгоритма Т(n) в следующем виде:

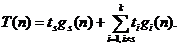
У операции s для числа выполняемых действий g_s(n)по определению одинаковой скорости роста с f_s(n) существуют такие значения n_0sÎ`N, С_1s>0, С_2s >0 , что при " n ³  n_0s  выполняется условие: С_1s f_s (n) ≤ g_s (n) ≤ С_2s f_s (n).

Рассмотрим остальные операции i (1 £ i  £ k , i ¹ s). Очевидно, g_i (n) ³0. По определению ограниченности сверхудля любой операции i существуют такие значения n_0iÎ N, С_2i >0 , что при " n ³ n_0i  выполняется условие: g_i (n) ≤ С_2i f_i (n).

Принимая:

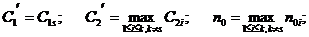
зависимость всех пар функций g_i(n), f_i(n)при " n ³ n₀ можно представить в унифицированном виде: g_i (n) ≤ С₂f_i (n), а для общего времени счета – записать неравенство:

      

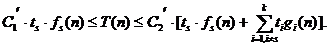
Поскольку все скорости роста f_i (n)при i ¹ s меньше скорости роста f_s (n), то по определению для константы С=1 всегда найдется такое значение параметра n¢_0i Î`N, что при "n³  n¢_0i  справедливо: f_i(n) ≤ f_s(n). Принимая в качестве n¢₀= max(n₀, n¢₀₁, … , n¢_ik), получим, что при " n ³ n¢₀ правое неравенство может быть представлено в виде:

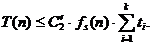 Вводя новые константы:

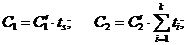получим, что при " n ³ n¢₀ выполняется соотношение, доказывающее справедливость теоремы:

С₁× f_s (n) ≤ T(n) ≤ С₂× f_s (n),

т.е. одинаковую скорость роста у общего времени счета T(n)и у максимальной из скоростей роста числа элементарных операций алгоритма, что и требовалось доказать.

При анализе элементарных арифметических операций алгоритма и подсчете их числа необходимо учитывать тип величин, с которыми выполняются данные действия. Представление целых и вещественных чисел в памяти ЭВМ различно. Операции с целыми числами в процессоре выполняет арифметико-логическое устройство, а операции с вещественными числами - сопроцессор для чисел с плавающей запятой.

Замечания. 1. Одинаковая скорость роста числа выполняемых операций может быть у нескольких элементарных операций. Справедливость доказанного утверждения при этом сохраняется.

2. Если у максимально растущих чисел операций g_i(n)скорость роста не является устойчивой, а известна лишь верхняя ее оценка, то справедлив следующий вариант теоремы 3.1.

Теорема 3.2 о верхней оценке скорости роста времени счета алгоритма. Пусть при выполнении алгоритма используются элементарные операции 1, ... , k. Числа этих операций g₁(n), … , g_k(n)ограничены сверху скоростью роста функции f(n).

Тогда при n→∞ скорость роста общего времени счёта алгоритма Т(n) также будет ограничена сверху скоростью роста функции f(n).

Доказательство Теоремы 3.2 можно выполнить по аналогии с доказательством Теоремы 3.1.

Следствие. Скорость роста общего времени счёта алгоритма Т(n) определяется скоростями роста f₁(n), ... , f_k(n) чисел элементарных операций g₁(n), ... , g_k(n) либо их верхними границами.

Скорость роста общего времени счёта алгоритма Т(n) называют сложностью алгоритма и обозначают через f(n).

В зависимости от сложности все комбинаторные алгоритмы делятся на несколько основных групп.

Полиномиальными называются алгоритмы, сложность которых ограничена полиномом.

Примеры 1: а) f(n) = n, б) f(n) = n ², в) f(n) = n×logn < n ².

Экспоненциальными называются комбинаторные алгоритмы, сложность которых в пределе при бесконечном возрастании n превышает полином любой степени.

Примеры 2: а) f(n) = е ⁿ, б) f(n) = n ⁿ, в) f(n) = n!, г) f(n) =2 ⁿ.

Субэкспоненциальными называются алгоритмы, сложность которых в пределе при бесконечном возрастании n превышает полином любой степени, но меньше 2 ^nδ при любом δ>0.

Пример 3. f(n) = n ^logn.

Рассмотрим примеры расчета сложности алгоритмов.

Пример 4. Задача: упорядочить по убыванию элементов линейный числовой массив А[n]_i.

Предлагаемый алгоритм решения: внутренняя (без использования дополнительной памяти) сортировка с выбором. В данном алгоритме выполняется n –1 шаг. На первом определяется минимальный из n элементов a₁, a₂, … , a_n и путем обмена с a₁ помещается на первое место. На втором определяется минимальный из n–1 элементов a₂, … , a_n и путем обмена с a₂ помещается на второе место и т.д.

Необходимо определить сложность алгоритма как функцию характерного числа задачи, которым является длина массива n.

Решение. В алгоритме используются две основные операции – 1) сравнение величин элементов массива и 2) обмены пар элементов местами. Определим в зависимости от параметра задачи n числа выполняемых основных операций. Обозначим их, соответственно, g₁(n) и g₂(n). Так как всего выполняется n –1 шаг, на каждом один обмен, то g₂(n) = n – 1. На первом шаге выполняется (n - 1) сравнение, на втором – (n –2), … , на последнем (n – 1) –том – одно сравнение. g₁(n) определяем как сумму арифметической прогрессии:

g₁(n) = (n – 1)+ (n –2)+…+1 = n(n -1)/2.

Так как для найденных функций выполняются следующие предельные оценки:

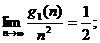
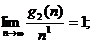
то по определению g₁(n) имеет квадратичную полиномиальную скорость роста, а g₂(n) – линейную.

Ответ: поскольку у операции сравнения 1 устойчивая квадратичная полиномиальная скорость роста, а у операции обмена 2 – устойчивая линейная скорость, то по Теореме 3.1 скорость роста общего времени счёта (сложность) алгоритма будет устойчивой и равна максимальной из скоростей роста чисел элементарных операций, т.е. будет квадратичной полиномиальной.

Пример. 5. Необходимо определить сложность алгоритма, заключающегося в  полном переборе обходов в задаче коммивояжера (ЗК) для n населенных пунктов {vⁿ }={v₁, v₂, ... , v_n}(пример 5 п.3.1).

Решение. На каждом из (n–1)!/2возможных обходов при полном переборе требуется выполнить следующие операции:

1) сформировать сам обход Оⁿ={v_i1, v_i2, ... , v_in} ,

2) вычислить длину обхода {v_i1, v_i2, ... , v_in} L(Оⁿ):

3) сравнить длину обхода L(Оⁿ) с текущим значением минимума L_min и при необходимости – скорректировать L_min.

Поскольку формирование обхода Оⁿ требует n элементарных операций, вычисление длины – также n сложений, то числа выполняемых операций g₁(n) (формирование обхода), g₂(n) (сложение), g₃(n) (сравнение длин обхода) будут следующими:

g₁(n)= n! /2, g₂(n)= n! /2, g₃(n)= (n–1)!/2 .

Для найденных функций выполняются следующие предельные оценки:

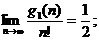
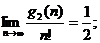
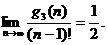
По Теореме 3.1 сложность алгоритма будет устойчивой и равна максимальной из скоростей роста чисел элементарных операций, т.е. будет факториальной по n.

Ответ: Сложность алгоритма относится к экспоненциальному типу.

Сравнительные значения величин функций для трёх рассмотренных типов скоростей роста при значениях характерного параметра n = 10, 100, 1000 приведены в таблице.

NN Вид алгоритма   Функция n = 10  n =100 n = 1000

                                           n ¹              10      10²        10³

                                                                  n×logn   10     2×10²   3×10³                                                                              

1. Полиномиальный    n ²               10²    10⁴        10⁶ 

                                          n ³              10³    10⁶         10⁹

                                          n¹⁰             10¹⁰  10²⁰        10³⁰

2. Субэкспоненциальный n^lnn    200,7 1,62×10¹³ 5,29×10²⁹                                      

                                          еⁿ    0.22×10⁵ 0.27×10⁴³ 0.78×10²⁰⁸

3. Экспоненциальный    2ⁿ      0.1×10⁴ 0.12×10³¹ 0.1×10³⁰¹

                                           n!  0.36 ×10⁷     10¹⁵⁸     4×10²⁵⁶⁷

                                          nⁿ                10¹⁰ 10²⁰⁰     10³⁰⁰⁰

---

Дата добавления: 2018-04-15; просмотров: 1255; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!