Погрешность функции. Прямая и обратная задачи теории погрешностей

⇐ ПредыдущаяСтр 2 из 2

Основная (прямая) задача теории погрешностей заключается в следующем: по известным значениям погрешностей исходных данных определить погрешность некоторой функции от этих величин. В обратной задаче задается погрешность функции и требуется найти обеспечивающие ее погрешности переменных функции.

2.5.1. Решение прямой задачи для функции одной переменной

Вначале рассмотрим функцию одной переменной f(x), определенную на вещественной оси R. Допустим, аргумент функции задан с погрешностью в точке х=а приближенным значением х=а*. Абсолютная погрешность задания аргумента: D(а^*) =½а - а*½. Необходимо найти предельную абсолютную погрешность D(f) значения функции f(x), вызванную ошибкой задания ее аргумента.

Рассмотрим для определенности случай а < а*, когда приближенное значение превышает точное и применим к функции f(x),на отрезке [а, а*] формулу конечных приращений или теорему Лагра́нжа о среднем значении [], которая утверждает, что если функция f непрерывна на отрезке [a; а*] и дифференцируема в интервале (a; а*) (т.е. в любой точке интервала существует конечная или бесконечная производная), то всегда найдётся такая средняя точка b интервала (b Î(a; а*)), для которой выполняется равенство:

(f(а*) - f(а))/(а* - а) = f¢(b)). (2.11)

Геометрический смысл формулы заключается в том, что у дифференцируемой во всех точках интервала (a; а*) функции f(x) всегда найдется точка b, в которой угол наклона касательной к графику равен углу наклону отрезка, соединяющего начальную (a;f(а)) и конечную (a*;f(а*)) точки графика (рис.2.1). Если функция недифференцируема хотя бы в одной точке (х=с, рис.2.2), то такой точки может не быть.

Рис.2.1.Дифференцируемая функция Рис.2.2. Недифференцируемая функция

В формуле (2.11) величина (f(а*) - f(а)) равна ошибке значения функции, вызванной погрешностью задания аргумента. Умножая обе части (2.11) на (а* - а) и переходя к модулям выражений, с учетом D(а^*) =½а - а*½ получим:

½f(а*) - f(а)½ = ½f¢(b)½×½а* - а½ = ½f¢(b)½× D(а^*). (2.12)

Если вместо ½f¢(b)½ в формулу (2.12) подставить значение max(½f¢(b)½), в котором b Î(a; а*)), то для искомой предельной абсолютной погрешности D(f) получим следующую оценку:

D( f(а^*)) £ max(½f¢(b)½) × D(а^*). (2.13)

В случае а > а* доказательство оценки выполняется аналогично. Отметим, что при заданном приближенном значении а^* возможное точное значение аргумента а может лежать на отрезке [а^*- D(а^*); а^*+ D(а^*) ] . В случае, если задано точное значение х=а, то приближенном значении а^* может лежать на отрезке [а- D(а^*); а+ D(а^*) ] .

Верхнюю оценку (2.13) назовем уточненной и обозначим D(f(а^*))_ут. Рассмотрим малые значения абсолютной погрешности аргумента. При D(а^*)®0 величина max(½f¢(b)½) в пределе стремится к ½f¢(а)½. Подставляя ее в (2.13), получим приближенную оценку (обозначим ее D(f(а^*))_пр) для предельной абсолютной погрешности D(f(а^*)):

D(f(а^*)) »½f¢(а)½× D(а^*) = D(f(а^*))_пр. (2.14)

Из (2.14) можно найти приближенную оценку для предельной относительной погрешности значения функции d(f(а)) = D(f(а))/½f(а)½ в зависимости от предельной относительной погрешности значения аргумента d(а) = D(а)/½а½:

d(f(а))=D(f(а))/½f(а)½»(½f¢(а)½/½f(а)½)×½а½×(D(а^*)/½а½)=

=½ln(f(а))¢½×½а½×d(а)/ =d(f(а))_пр. (2.15)

Как следует из полученных оценок (2.13) - (2.15), вычисление функции в точке с большим модулем первой производной может привести к значительному увеличению погрешности результата по сравнению с погрешностью аргумента.

Пример 1. Задана функция f(x) = х²+х-4 в точке x = а =-1 при заданной величине абсолютной погрешности аргумента D(а^*) = 0,1. Найти в заданной точке x =-1:

а) уточненное D(f(-1))_ут и приближенное D(f(-1))_пр значения предельной абсолютной погрешности функции,

б) приближенное d(f(-1))_пр значение предельной относительной погрешности функции.

Решение. Первая производная функции f¢(x) = 2х+1. Модуль данной линейной функции является монотонной функцией, если на исследуемом отрезке она не меняет знак. Следовательно, при выполнении данного условия максимум ½f¢(х)½ достигается в какой-либо из крайних точек. Поскольку задано точное значение аргумента, то приближенное значение может лежать на отрезке [-1- 0,1 = -1.1; -1+ 0,1 = -0.9]. Так как f¢(-1.1) = -1,2; f¢(-0.9) = -0,8; то max(½f¢(b)½)=1,2 и из формулы (2.13) получим, что уточненное предельное значение абсолютной погрешности

D(f(-1))_ут = 1,2 × 0,1 = 0,12.

Приближенное значение абсолютной погрешности находим по формуле (2.14) с учетом f¢ (-1) = -1:

D( f(-1))_пр = 1 × 0,1 = 0,1.

Предельную относительную погрешность значения функции находим по формуле (2.15) с учетом f(-1) = 1-1- 4 = -4 и d(-1) = 0,1/1 = 0,1:

d(f(-1))_пр = (1/4) ×1×0,1=0,025.

2.5.2. Решение прямой задачи для функции многих переменных

Рассмотрим задачу определения предельного значения абсолютной погрешности функции f(`x ) = f(x₁, x₂,..., x_n), зависящей от n переменных x₁, x₂,..., x_n, определенных на вещественной оси R.

Допустим, аргумент функции задан с погрешностью в точке `х=`а = (а₁, а₂,..., а_n) приближенным значением `х=`а* = (а₁*, а₂*,..., а_n*). По каждой переменной x_i ( i = 1,...,n) введем абсолютную погрешность: D(`а_i^*) =½а_i - а_i*½. Найдем оценки для предельной абсолютной погрешности Df(`а^* ) значения функции f(`x ) в точке`х=`а, вызванную ошибкой задания ее аргумента.

По аналогии с функцией одной переменной к функции f(`x ) применим на параллелепипеде Р, образованном декартовым произведением отрезков [а₁, а₁*],[а₂, а₂*],...,[а_n, а_n*] (Р = [а₁, а₁*]´[а₂, а₂*]´...´[а_n, а_n*]), формулу конечных приращений Лагранжа о среднем значении, которая утверждает, что если функция f непрерывна на множестве Р и дифференцируема внутри Р, то внутри Р всегда найдётся такая средняя точка`b параллелепипеда (`b Î Р), для которой выполняется равенство:

(f(`а*) - f(`а)) = (¶(f(`x ))/¶x₁)½_`_x₌_`_b ×(а*₁ - а₁) + (¶(f(`x ))/¶x₂)½_`_x₌_`_b ×(а*₂ - а₂) + … + (¶(f(`x ))/¶x_n)½_`_x₌_`_b ×(а*_n - а_n). (2.16)

Геометрический смысл точки`b аналогичен одномерному случаю. В ней проекции касательной плоскости на оси наклонены под теми же углами, что и соответствующие диагонали на гранях Р. Применяя аналогичный вывод и обозначая через max(¶(f(`x ))/¶x_i) максимальное значение частной производной от функции f(`x ) по переменной x_i на параллелепипеде Р, получим уточненную оценку для абсолютной погрешности функции Df(`а^* ) в зависимости от абсолютных погрешностей переменных x₁, x₂,..., x_n:

Df(`а^*)=½(f(`а*) - f(`а))½£ max½¶(f(`x))/¶x₁½ × D(а₁^*) + max½¶(f(`x))/¶x₂½×D(а₂^*) +…+ max½¶(f(`x))/¶x_n½×D(а_n^*) = Df(`а^*)_ут. (2.17)

Приближенная оценка для абсолютной погрешности функции Df(`а^* ) в зависимости от абсолютной погрешности переменных x₁, x₂,..., x_n, полученная при условии а₁* ®а₁, а₂*® а₂,..., а_n*®а_n, равна:

Df(`а^*)»½¶(f(`x))/¶x₁)½_`_x₌_`_а½×D(а₁^*)+½¶(f(`x))/¶x₂)½_`_x₌_`_а ½×D(а₂^*) +…+

½¶(f(`x))/¶x_n)½_`_x₌_`_а ½×D(а_n^*)= Df(`а^*)_пр. (2.18)

Приближенная (df(`а^*)_пр) оценка для относительной погрешности функции Df(`а^* ) в зависимости от относительных погрешностей переменных x₁, x₂,..., x_n будет следующей:

d(f(`а))=D(f(`а))/½f(`а)½»½¶(lnf(`x))/¶x₁)½_`_x₌_`_а½×½x₁^*½×d (а₁^*)+

½¶(lnf(`x))/¶x₂)½_`_x₌_`_а ½×½x₂^*½×d(а₂^*) +…+½¶(lnf(`x))/¶x_n)½_`_x₌_`_а ½×½x_n^*½d (а_n^*) = df(`а^*)_пр.. (2.19)

Пример 2. Оценить для точки на эллипсоиде, заданном формулой

приближенные значения предельных абсолютной погрешности D( z)_пр и относительной погрешности d( z)_пр положения точки на эллипсе по координате z при заданных значениях координат x=3, у=2 и их абсолютных погрешностях D(x) = 0,1 и D(у) = 0,2.

Решение. Выразим зависимость z(x,y) и определим ½z(3,2)½:

Общий вид частных производных функции z(x,y) по переменным x,y, их абсолютные значения в точке (3,2):

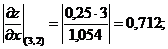
Приближенную оценку для абсолютной погрешности функции Dz(x,y) получаем из (2.18): Dz(x,y) » 0,1054 ×0,1 +0,304×0,2 = 0,0713.

Приближенную оценку для относительной погрешности функции dz(x,y) при известной оценке Dz(x,y) проще получить, используя определение относительной погрешности: dz(x,y) = Dz(x,y) / z(x,y) = 0,0713/1,054 = 0,0677.

2.5.3. Обратная задача теории погрешностей

Обратная задача теории погрешностей заключается в определении такой точности задания значения аргумента функции x=а, при котором ее предельная абсолютная погрешность не превосходила бы заданной величины e: D(f(а)) = e.

Задачу решают с использованием приближенных оценок абсолютных погрешностей. Для функции одной переменной f(x)из оценки (2.14) D( f(а)) » ½f¢(а)½× D(а^*) = e следует однозначное решение:

D(а^*) = e/½f¢(а)½. (2.20)

В случае функций нескольких переменных f(`x ) = f(x₁, x₂,..., x_n) задача является математически не определенной, поскольку заданная предельная абсолютная погрешность функции D(f(`а ))=e может быть обеспечена при любом наборе предельных абсолютных погрешностей переменных D(а₁^*), D(а₂^*), …, D(а_n^*), которые в соответствии с оценкой (2.18) удовлетворят условию:

½¶(f(`x))/¶x₁)½_`_x₌_`_а½×D(а₁^*)+½¶(f(`x))/¶x₂)½_`_x₌_`_а ½×D(а₂^*) +…+½¶(f(`x))/¶x_n)½_`_x₌_`_а ½×D(а_n^*) = e. (2.21)

Простейшее однозначное решение обратной задачи дает принцип равных влияний, по которому вклады всех аргументов в формирование абсолютной погрешности функции e принимают одинаковыми и равными e/n:

½¶(f(`x))/¶x_i)½_`_x₌_`_а ½×D(а_i^*)=e/n, (i=1,...,n). (2.22)

Условие (2.22) фактически сводит многомерную задачу к одномерной. По аналогии с (2.20) получим следующие величины абсолютных погрешностей переменных:

D(а_i^*)=(e/n) / ½¶(f(`x))/¶x_i)½_`_x₌_`_а ½, (i=1,...,n). (2.22)

Основным недостатком решения обратной задачи по принципу равных влияний (2.22) является то, что расчетные значения абсолютных погрешностей D(а_i^*) у отдельных переменных могут стать настолько малыми, что вычислить или измерить эти величины с такой точностью практически невозможно. В этом случае отступают от принципа равных влияний и увеличивают долю погрешности таких переменных за счет уменьшения доли других.

Вопросы для проверки знаний.

1. Какую задачу теории погрешностей называют прямой, а какую обратной ?

2. В чем заключается геометрический смысл формулы Лагранжа конечных приращений для функций одной переменной и функций нескольких переменных ?

3. В чем заключается отличие уточненной оценки абсолютной погрешности функции от приближенной ?

4. В чем заключается обратная задача теории погрешностей ?

5. Как решается обратная задача теории погрешностей для функций одной переменной ?

6. Почему обратная задача теории погрешностей для функций нескольких переменных в общем случае не имеет единственного решения ?

7. В чем заключается принцип равных влияний при решении обратной задачи для функций нескольких переменных ?

Список литературы

Дата добавления: 2018-04-15; просмотров: 2601; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!