Передаточная функция включенных последовательно звеньев с импульсными элементами не равна произведению их передаточных функций.

Динамика цифровых систем

Следящий привод, работающий совместно с цифровой управляющей машиной (ЦУМ), называется цифровым следящим приводом (ЦСП). Наличие ЦУМ влияет как на динамические свойства следящего привода, так и на методы их определения. Степень влияния зависит от структуры ЦСП – способа связи ЦУМ и следящего привода.

Привод может быть соединен с ЦУМ последовательно (рис. 1), а между ними установлен цифроаналоговый преобразователь (ЦАП). На устойчивость следящего привода ЦУМ не оказывает влияния и она определяется устойчивостью непрерывной части.

Рис. 1 – Последовательная функциональная схема ЦСП

Импульсный элемент может ( ) может находиться внутри замкнутого контура и оказывать влияние на устойчивость ЦСП (рис. 2). В общем случае специализированному микропроцессорному вычислителю (СМВ) может быть поручена дискретная экстраполяция (ДЭ) и коррекция (ДК). Наличие импульсного элемента приводит к появлению в структурной схеме передаточной функции экстраполятора (Рис.3).

Рис. 2 – Структурная схема привода с импульсным управлением

Функции микропроцессора может выполнять и сама ЦУМ. Структурная схема привода в этом случае остается без изменения, а импульсный элемент, имеющий ранее период квантования , в этом случае имеет период квантования (рис. 4).

Рис. 3 – Функциональная схема ЦСП с микропроцессором

Линейная динамическая модель определяет основу динамической структуры дроссельного привода и дает достаточно полное представление о его быстродействии, частоте собственных колебаний и в первом приближении определяет устойчивость контура следящей гидравлической системы, в которой он применяется. Линейная динамическая модель гидравлического привода составляется на основе его линеаризованных уравнений.

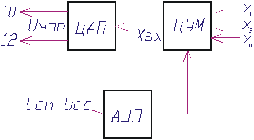
Рис. 4 – Функциональная схема с замыканием через ЦУМ

1. Дискретные преобразования Лапласа

Основной причиной, влияющей на динамические свойства ЦСП, является квантование по времени, в то время как квантование по уровню можно не учитывать. При исследовании дискретных систем регулирования приходится иметь дело с различными моделированными импульсами. Как правило, это широтная или амплитудная модуляция, а импульсы имеют прямоугольную форму.

На рис. 5 и рис. 6 представлены различные виды модулированных сигналов.

Рис. 5 - Амплитудно-импульсная модуляция

Рис. 6 - Широтно-импульсная модуляция

Входной управляющий сигнал считаем дискретным, с постоянным периодом квантования 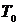и тогда для -го импульса можно записать .

Преобразования Лапласа ставит в соответствие функции действительной переменной функцию комплексной переменной с помощью соотношения

Вид дискретной функции может иметь различный характер. Рассмотрим случай, когда дискретная функция представляет собой последовательность импульсов, а интеграл Лапласа будет представлять бесконечную сумму изображений всех импульсов, образующих импульсную функцию [1]. Тогда можно представить интеграл Лапласа для решетчатой функции, учитывая выражение , в виде

Наличие множителя не играет существенной роли и последний может быть опущен.

Положив , мы получим - преобразование дискретной функции:

Аналогично свойствам и правилам обычного преобразования Лапласа существуют идентичные свойства и правила дискретного преобразования Лапласа

Проведем - преобразование единичной функции Хевисайда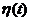

Импульсный фильтр – непрерывная часть системы совместно с ключом на ее входе (рис. 7). Ключ замыкается в определенные моменты 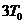времени ( , , ,…, ) и сигнал на выходе ключа, как и на выходе непрерывной части, рассматриваются в эти промежутки времени.

На входе непрерывной части 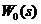после ключа действует дискретная функция , или в относительных координатах , а на выходе - .

Рис. 7 – Импульсный фильтр

Действующая на входе непрерывной функции 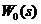дискретная функция может быть представлена в виде последовательности дельта функций , а на выходе будет непрерывная функция , определяемая в те же моменты времени ( , , ,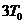…, ). При таком определении функция носит название решетчатой функции.

Пусть имеем изображение входной величины

изображение выходной величины

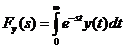передаточную функцию

Отсюда получаем

Перейдем к конечному интервалу времени , ,

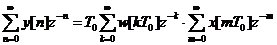Выражение

представляет собой передаточную функцию импульсного фильтра.

Передаточная функция включенных последовательно звеньев с импульсными элементами не равна произведению их передаточных функций.

Вычисление передаточной функции системы регулирования с импульсными элементами осуществляется следующим образом:

Для непрерывной части системы вычисляется функция веса - .

Определяется (обычно по таблицам) для найденной функции времени соответствующее - преобразование, которое умножаем на .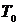

Для примера рассмотрим некоторую функцию на интервале , тогда можем записать

В полученном выражении делаем подстановку и и получаем

, ,

тогда

Для сложных случаев приходится разлагать передаточную функцию непрерывной части на простейшие дроби и представлять функцию веса в виде суммы слагаемых, для каждого их которых имеется табличное значение - преобразования.

Вид передаточной функции зависит от характера импульсного звена. Например, если мы имеем квантование по уровню сигнала и по времени, то передаточную функцию импульсного звена можно представить в виде экстраполятора нулевого порядка, поскольку передаточная функция на интервале дискретности апроксимируется полиномом нулевого порядка.

Существо заключается в том, что экстраполятор как бы запоминает значение решетчатой функции (поданный на его вход сигнал) на весь период квантования и его передаточная функция не зависит от номера интервала. Передаточная функция системы регулирования имеет вид

Для нахождения передаточной функции необходимо найти переходную функцию непрерывного звена, провести с ней - преобразование, затем умножить на передаточную функцию экстраполятора.

Рассмотрим апериодическое звено

Переходная функция апериодического звена представляет собой решение уравнения

и имеет вид

а весовая функция

Для нашего апериодического звена имеем переходную функцию

Получаем передаточную функцию системы регулирования

2.Устойчивость импульсных систем регулирования

Для исследования уравнений высокого порядка используется, так называемое, - преобразование

, .

После подстановки получаем

где - относительная псевдочастота.

Иногда вводится понятие абсолютной псевдочастоты - .

При малых частотах действительная частота и псевдочастота совпадают, и при для передаточной функции с - преобразованием могут использоваться те же самые критерии, что и для непрерывных систем, например, метод логарифмических частотных характеристик.

Оценка качества импульсной системы регулирования может проводиться по виду переходного процесса.

В качестве примера рассмотрим передаточную функцию интегрирующего звена

, ,

соответствующая ему передаточная функция после - преобразований имеет вид

Учитывая, что

, ,

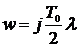получаем

Отличие от обычного интегрирующего звена заключается в наличии неминимально-фазового звена, амплитуда и сдвиг фаз которого равны

, ,

На рис. 8 представлены логарифмические амплитудно-частотные характеристики интегрирующего звена.

Рис. 8 – Логарифмические частотные характеристики интегрирующего звена

Таким образом, если идеальный привод с интегрирующим звеном всегда устойчив, имеет запас по фазе , то при работе в импульсной системе при некотором коэффициенте усиления может оказаться на границе устойчивости.

Рассмотрим передаточную функцию апериодического звена

, ,

соответствующая ему передаточная функция после - преобразований имеет вид

получаем

Отличие от обычного апериодического звена заключается в наличии неминимально-фазового звена, что приводит к снижению запаса устойчивости по фазе и амплитуде.

На рис. 9 представлены логарифмические амплитудно-частотные характеристики апериодического звена.

Рис. 9 – Логарифмические частотные характеристики апериодического звена

Передаточная функция колебательного звена имеет вид

Выражение для определения передаточной функции имеет достаточно громоздкий вид и, ограничимся поэтому, общими рекомендациями, поскольку провести, например, - преобразования в системе Mathcad для любой функции является несложным.

Алгоритм исследования логарифмических амплитудно-частотных характеристик следующий.

1. Находим систему линейных дифференциальных уравнений, характеризующих поведение нашей системы регулирования.

2. Определяем переходную функцию непрерывной части системы регулирования - , решив систему дифференциальных уравнений или проведя обратные преобразования Лапласа.

3. Определяется для найденной функции времени соответствующее - преобразование и, умножив на передаточную функцию экстраполятора нулевого порядка, получаем передаточную функцию системы регулирования.

4. Применив к передаточной функции - преобразования определяем амплитуду (подстановкой 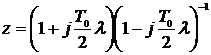) и фазу системы регулирования в зависимости от псевдочастоты - и .

5. Строим логарифмические псевдочастотные характеристики и определяем запасы по фазе и амплитуде.

На рис. 10 представлены логарифмические псевдочастотные характеристики колебательного звена, когда

, , , , , , .

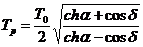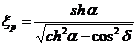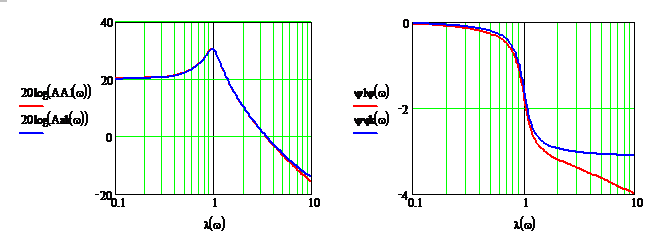Рис. 10 – Логарифмические частотные характеристики колебательного звена.

Логарифмические псевдочастотные характеристики подтверждают тот очевидный факт, что чем меньше период квантования по сравнению с постоянной времени привода, тем меньше влияние импульсного элемента на устойчивость привода. Таким образом, для обеспечения устойчивости импульсной системы необходимо, чтобы частота 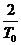была расположена на 0,5…1 декаду правее частоты среза непрерывной части [3].

Динамическую точность импульсной системы можно оценить по ошибке регулирования, которая возникает при изменении входной координаты с постоянной скоростью

Тогда ошибка регулирования будет равна

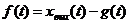Другими словами на вход привода подается ступенчатый входной сигнал со ступеньками одинаковой высоты. На рис. 11 представлена реакция импульсной системы на входной сигнал с постоянной скоростью.

- изменение входного импульсного сигнала, - изменение выходного сигнала апериодического звена, - изменение выходного сигнала колебательного звена, -изменение скорости апериодического звена, 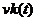-изменение скорости колебательного звена.

Рис. 11 – реакция системы на сигнал с постоянной скоростью

На рис. 12 для рассмотренных звеньев показана ошибка регулирования.

-установившаяся ошибка по положению апериодического звена, -установившаяся ошибка по положению колебательного звена, -установившаяся ошибка по скорости апериодического звена, -установившаяся ошибка по скорости колебательного звена,

Рис. 12- Установившиеся ошибки апериодического и колебательного звеньев

Дата добавления: 2018-04-15; просмотров: 207; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!