Значения эффективности вариантов систем по различным критериям качества
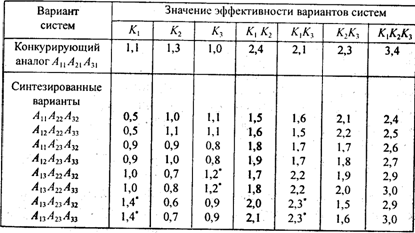
Анализ приведенных результатов показывает, что по критериям К1 и К1K3 две новые синтезированные системы: (А13А23А32) и (А13А23А33), а по критерию К3, также две системы: (А13А22А32) и (А13А22А33) значительно эффективнее конкурирующего объекта. Эти системы отмечены звездочкой (см. табл. 5.24).
По критерию K2 и сочетаниям критериев К1К2, К2К3, К1К2К3 конкурирующий объект превосходит в эффективности все синтезированные новые варианты систем.
Морфологический синтез систем по критерию комбинационной новизны
Критерий комбинационной новизны численно характеризует для представленного в морфологической таблице класса систем новые сочетания функциональных подсистем. Этот критерий определяется по формуле
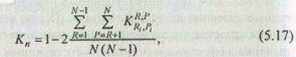
где N — число строк в морфологической таблице (число функциональных подсистем);
Ri и Рi — номера столбцов морфологической таблицы соответственно в строках R и Р, альтернативы из которых вошли в i-ю систему;
К — переменная; К = 1, если альтернатива из строки R и столбца Ri образовала известную комбинацию с альтернативой из строки Р и столбца Рi; К = 0, если эта комбинация ранее была неизвестна в пределах рассматриваемого класса объектов.
Определение критерия комбинационной новизны для каждой системы осуществляется на основании матриц комбинационных связей альтернатив. Построение указанных матриц ведется в соответствии со следующими принципами. Рассматривается морфологическая таблица, содержащая N строк. Для всех альтернатив i-й строки формально отражаются комбинационные связи с альтернативами, содержащимися во всех остальных строках морфологической таблицы:
|
|
|
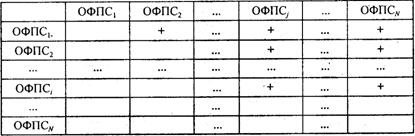
В приведенной матрице плюсами обозначены взаимосвязи между функциональными подсистемами, альтернативы которых необходимо попарно оценить по признаку новизны. Для альтернатив каждой пары функциональных подсистем ОФПСi и ОФПСj строятся матрицы комбинационных связей альтернатив Кij = {Кlrij}, l = 1,..., пi; r = 1,..., nj, где пi и пj — соответственно число альтернатив в i-й и j-й строках морфологической таблицы. Число матриц К = {Кij} определяется по формуле
Nk = N ( N - 1 )/ 2,
где N — число строк морфологической таблицы.
Рассмотрим пример вычисления критерия комбинационной новизны. Пусть задана исходная морфологическая таблица (табл. 5.25).
Таблица 5.25
Морфологическая таблица
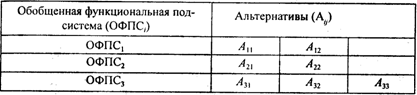
На основании морфологической таблицы с учетом экспертной информации строится Nk =3(3 -1 )/2=3 матриц {Кlrij} парных комбинационных связей альтернатив Аij. Здесь верхние индексы указывают номера сравниваемых обобщенных функциональных подсистем, а нижние индексы — количество альтернатив двух сравниваемых подсистем.
|
|
|
Матрицы парных комбинаций имеют следующий вид:
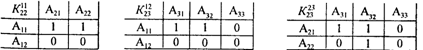
Содержание матрицы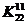 
свидетельствует о том, что для альтернативы A11 известны решения, в которых она участвовала в сочетании с альтернативами A21 или А22, а для альтернативы A12 не известны случаи ее участия в комбинациях с альтернативами A21 и А22.Значения критерия комбинационной новизны для 12 синтезированных на морфологической таблице (см. табл. 5.25) вариантов (Si) рассчитаны с учетом формулы (5.17):
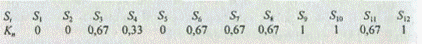
Большей новизной обладают те решения, у которых наибольшее значение критерия комбинационной новизны. В рассматриваемом случае к таким решениям относятся Sy, S\g, S^.
Дата добавления: 2018-04-15; просмотров: 261; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!