Основные этапы построения и исследования систем-классификаций
Первым этапом классификационных построений является глубокое проникновение в суть рассматриваемых явлений и выбор соответствующего принципа классификации.
Второй этап — установление списка признакови их значений, подлежащих учету на отдельных объектах. В список включаются признаки, наиболее полно характеризующие изучаемые объекты в смысле заданной цели. Из рассмотрения исключаются признаки, имеющие слабые разделительные свойства.
Третий этап — отбор репрезентативной выборки объектов и производство измерений.
Четвертый этап — выбор отношений на множестве описаний объектов; мер, порождающих отношения; решающих правил и критериев эффективности. Здесь же производятся вычисления.
Пятый этап — построение и анализ структурной схемы системы, в которой связи между элементами соответствуют выполнению отношений между ними. Способом представления структурных схем являются графы и дендрограммы.
Шестой этап — интерпретация полученных результатов, т. е. перенос полученных утверждений с системы-модели на систему-прототип.
Первые три этапа построения систем-классификаций составляют творческую часть процедуры классификации, которая целиком зависит от исследователя и не может быть формализована.
На четвертом и пятом этапах классификации требуется перерабатывать большой объем информации по определенным правилам логики. В связи с этим актуальной становится задача формализации процедур на этих этапах и реализации их в виде компьютерных систем.
|
|
|
Виды измерений
Системы, подлежащие классификации, изучаются прежде всего относительно наличия у них характерных свойств или состояний, которые отражаются различными признаками. Значения признаков могут измеряться с различной точностью.
Для измерения признаков применяются шкалы наименований, порядка, отношений, балльные, интервалов.
При использовании шкалы наименований указывается только, одинаковы или нет объекты относительно измеряемого признака.
Порядковые или ранговые признаки сравниваются только по отношению "больше — меньше".
Более точные измерения предполагают и большее число значений. В этом случае используются балльные шкалы. Значения балльной шкалы представляют собой ограниченный дискретный ряд чисел, отстоящих друг от друга на одинаковом расстоянии.
При дальнейшем увеличении точности измерений число значений можно увеличивать, доводя его до максимально осуществимого.
Условно все виды оценок делят на качественные и количественные. В соответствии с рекомендациями, приведенными в работе [4], качественными можно считать только те из них, которые измеряются в шкале наименований.
|
|
|
Формализация обработки качественных признаков
Множество вариантов, систематизированных в морфологических таблицах, может быть отражено списком качественных признаков. Список признаков, определяющий вариант морфологического множества, представляет его признаковый образ. Количество признаковых образов и собственно признаков, используемое в конкретном исследовании, может быть достаточно большим. Это делает морфологическое множество труднообозримым и малодоступным для анализа на умозрительном уровне.
Более четкие результаты могут быть получены при использовании математических методов, специально предназначенных для сжатия информации и количественной характеристики интегрированных свойств анализируемого материала.
Множество образов вариантов систем может быть представлено как матрица, имеющая q столбцов и р строк (порядка p х q), причем номеру столбца соответствует наименование системы Sj (j = 1, 2, ... , q), а номеру строки — название признака Zi (i =1, 2,..., р). В ряде случаев номеру строки ставится в соответствие значение признака. Информационным содержанием матриц являются указания о присутствии или отсутствии каждого из учитываемых признаков в рассматриваемых системах. При этом если i-й признак присутствует в j-й системе, то на пересечении i-й строки и j-ro столбца помещается "1", в противном случае — "0".
|
|
|
Любой j-й столбец матрицы назовем описанием j-й системы, любую i-ю строку — описанием i-го признака. В терминах теории множеств

Формула (5.1) читается: семейство множеств S, состоящееизвсех Sj, таких, у которых элементы j принадлежат множеству J. Аналогично семейство множеств
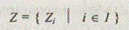
есть индексированное множество, а I — индексное множество:

Индексация позволяет различать множества, состоящие из одинаковых элементов.
Пример матрицы образов представлен в табл. 5.3.
Таблица 5.3
Дата добавления: 2018-04-15; просмотров: 387; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
