Производная функции одной переменной.
Государственное образовательное учреждение высшего профессионального образования
НОВОУРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ
Кафедра высшей математики
Пределы.
Непрерывность.
Производная функции
Одной переменной
Учебно-методическое пособие по курсу «ВЫСШАЯ МАТЕМАТИКА»
для студентов всех специальностей всех форм обучения
Новоуральск 2004
УДК 519 О − 66
ББК 22.171
УДК 519 О − 66
ББК 22.171
МиМ − 2.3. − __________ −04
Пределы. Непрерывность.
Производная функции одной переменной
Учебно-методическое пособие по курсу «ВЫСШАЯ МАТЕМАТИКА»
для студентов всех специальностей всех форм обучения
Новоуральск, изд. НГТИ. − 60 с.
Пособие составлено ст. преподавателем кафедры высшей математики НГТИ Орловым Юрием Владимировичем.
Пособие содержит 30 вариантов контрольного задания по теме «Пределы. Непрерывность. Производная функции одной переменной» для домашних контрольных работ по данным темам. В пособии приведен пример решения одного из вариантов и справочник с необходимыми формулами и правилами.
Пособие обсуждено на заседании кафедры высшей математики НГТИ и рекомендовано к использованию в учебном процессе студентами всех специальностей заочной формы обучения.
|
|
|
“____”______________200 ___ г.
Зав. кафедрой к.ф.м.н. ___________________ А.П. Золотарёв
Согласовано:
Председатель методической комиссии:
Профессор, д.т.н. ___________________________ А.Е. Беляев
Содержание
| 1 | Контрольное задание по теме «Предел. Непрерывность. Производная функции одной переменной» (30 вариантов) …………………………………. | 4 |
| 2 | Пример решения варианта №31 контрольного задания ………. | 35 |
| 3 | Справочник …………………………………………..................... | 52 |
| 4 | Рекомендуемая литература ……………………………………… | 59 |
Пособие предназначено для проведения типовой работы (домашней контрольной работы) в группах первого курса заочной формы обучения, изучающих математический анализ. Пособие содержит задания по темам «Предел и непрерывность функции» и «Дифференциальное исчисление функции одной переменной». Каждый студент находит свой порядковый номер N в списке группы, по нему выбирает вариант контрольного задания. Если номер N превосходит 30, то студент выполняет вариант задания под номером N – 30.
|
|
|
Контрольная работа может быть разбита на две части. При решении контрольной работы по теме «Предел и непрерывность» каждый студент выполняет в своём варианте задания под номерами 1 и 2. При решении контрольной работы по теме «Производная функции одной переменной» каждый студент выполняет в своём варианте задания под номером 3.
Контрольные выполняются в соответствии со стандартом оформления текстовых документов. На титульном листе должно присутствовать название института (НГТИ), кафедры (высшей математики), номер контрольной по курсу «Математический анализ» с указанием варианта, фамилии и инициалов выполнившего с указанием группы, фамилии проверяющего и города Новоуральск с указанием года выполнения.
После подробной записи каждого из заданий должно приводиться его аккуратное решение с объяснением логических переходов и применяемых формул. После решения отдельно записывается ответ на все поставленные вопросы.
|
|
|
При решении контрольного задания рекомендуется воспользоваться конспектами лекций и литературой из приведённого в конце пособия списка. Автор рекомендует студенту при решении своего варианта внимательно разобраться с примером решения варианта, приведённом в данном пособии.
Контрольное задание
Вариант №1
№1 Вычислить пределы
1)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  ;
;
2)  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №2
№1 Вычислить пределы
1)  при а1=0, а2=2, а3= -1, а4=
при а1=0, а2=2, а3= -1, а4=  ;
;
2)  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
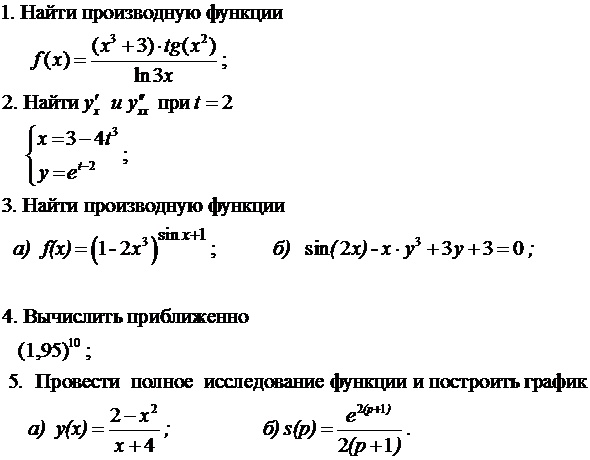
Вариант №3
№1 Вычислить пределы
1)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  ;
;
2)  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
|
|
|
№3

Вариант №4
№1 Вычислить пределы
1) 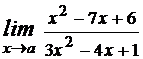 при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  ;
;
2)  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №5
№1 Вычислить пределы
1)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  ;
;
2)  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №6
№1 Вычислить пределы
1) 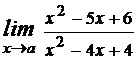 при а1=0, а2=2, а3= -1, а4=
при а1=0, а2=2, а3= -1, а4=  ;
;
2)  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №7
№1 Вычислить пределы
1)  ;
;
2)  ;
;
3)  при а1=0, а2=2, а3= -1, а4=
при а1=0, а2=2, а3= -1, а4=  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №8
№1 Вычислить пределы
1)  ;
;
2)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №9
№1 Вычислить пределы
1)  ;
;
2)  ;
;
3)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №10
№1 Вычислить пределы
1)  при а1=0, а2=2, а3= -1, а4=
при а1=0, а2=2, а3= -1, а4=  ;
;
2)  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №11
№1 Вычислить пределы
1)  ;
;
2)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №12
№1 Вычислить пределы
1)  при а1=0, а2=2, а3= -1, а4=
при а1=0, а2=2, а3= -1, а4=  ;
;
2)  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №13
№1 Вычислить пределы
1)  ;
;
2)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №14
№1 Вычислить пределы
1) 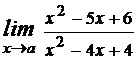 при а1=0, а2=2, а3= -1, а4=
при а1=0, а2=2, а3= -1, а4=  ;
;
2)  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №15
№1 Вычислить пределы
1)  ;
;
2)  ;
;
3)  при а1=0, а2=2, а3= -1, а4= +
при а1=0, а2=2, а3= -1, а4= +  .
.
№2 Найти область определения функции у=f(x),
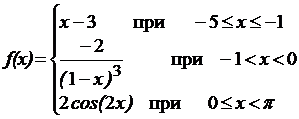 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
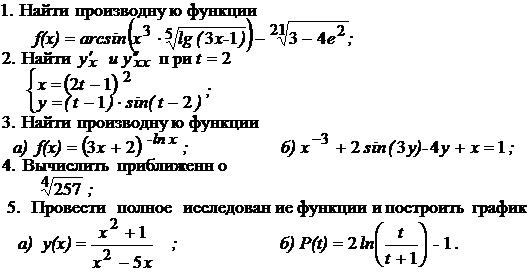
Вариант №16
№1 Вычислить пределы
1)  ;
;
2)  при а1= -2, а2=2, а3= -1, а4=
при а1= -2, а2=2, а3= -1, а4=  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №17
№1 Вычислить пределы
1)  ;
;
2)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №18
№1 Вычислить пределы
1)  при а1=0, а2=2, а3= -1, а4=
при а1=0, а2=2, а3= -1, а4=  ;
;
2)  ;
;
3) 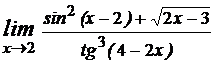 .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов.
№3

Вариант №19
№1 Вычислить пределы
1)  ;
;
2)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  ;
;
2)  ;
;
3).
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №20
№1 Вычислить пределы
1)  ;;
;;
2)  ;
;
3) 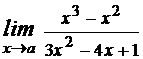 при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №21
№1 Вычислить пределы
1)  ;
;
2)  ;
;
3)  при а1=0, а2=3, а3= -1, а4=
при а1=0, а2=3, а3= -1, а4=  .
.
№2 Найти область определения функции у=f(x),
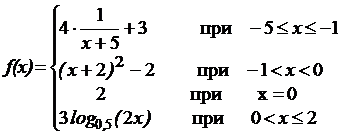 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
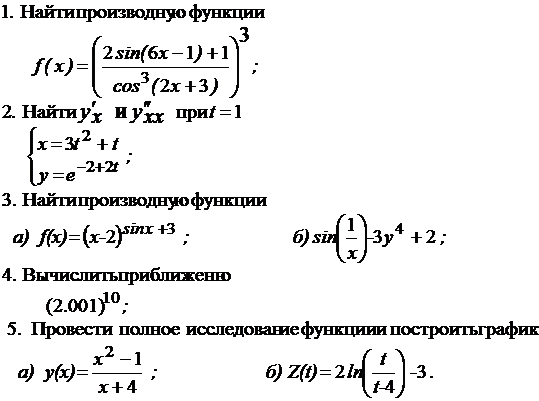
Вариант №22
№1 Вычислить пределы
1) 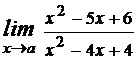 при а1=0, а2=2, а3= -1, а4=
при а1=0, а2=2, а3= -1, а4=  ;
;
2)  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
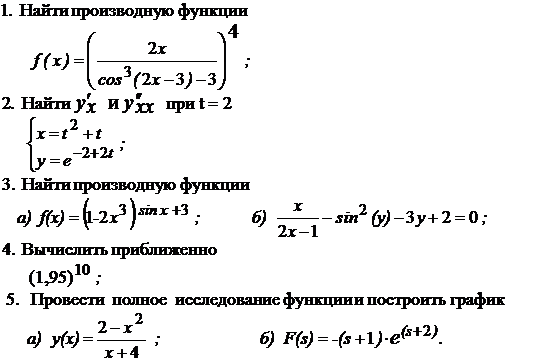
Вариант №23
№1 Вычислить пределы
1)  ;
;
2)  ;
;
3)  при а1=0, а2=-2, а3= -1, а4=
при а1=0, а2=-2, а3= -1, а4=  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №24
№1 Вычислить пределы
1) 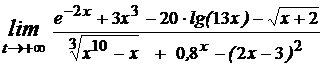 ;
;
2)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №25
№1 Вычислить пределы
1)  ;
;
2)  ;
;
3)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №26
№1 Вычислить пределы
1) 
2)  при а1=0, а2=2, а3= -1, а4=
при а1=0, а2=2, а3= -1, а4=  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №27
№1 Вычислить пределы
1)  ;
;
2)  при а1=0, а2=1, а3= -1, а4=
при а1=0, а2=1, а3= -1, а4=  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №28
№1 Вычислить пределы
1)  ;
;
2)  ;
;
3)  при а1=0, а2=2, а3= -1, а4=
при а1=0, а2=2, а3= -1, а4=  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №29
№1 Вычислить пределы
1)  ;
;
2)  при а1=6, а2=1, а3= -1, а4=
при а1=6, а2=1, а3= -1, а4=  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3

Вариант №30
№1 Вычислить пределы
1)  при а1=0, а2=2, а3= -1, а4=
при а1=0, а2=2, а3= -1, а4=  ;
;
2)  ;
;
3)  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
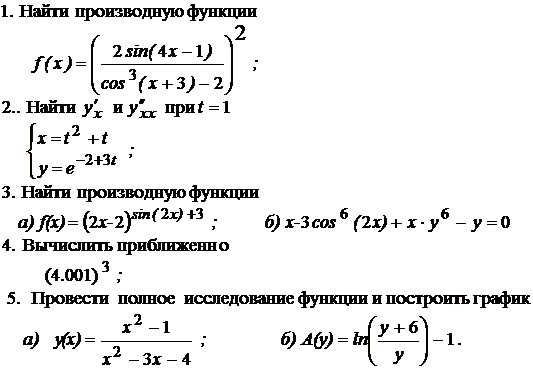
Вариант №31 (пример)
№1 Вычислить пределы
1)  ;
;
2)  ;
;
3)  при а1=1, а2=0, а3= 3, а4= -
при а1=1, а2=0, а3= 3, а4= -  .
.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
№3
1. Найти производную функции
 ;
;
2. Найти  , составить уравнения касательной и нормали
, составить уравнения касательной и нормали
при  для
для 
 ;
;
3. Найти производную функции
а)  ; б)
; б)  ;
;
4. Вычислить приближенно
 ;
;
5. Провести полное исследование функции и построить график
а)  ; б)
; б)  .
.
Пример решения варианта
Контрольного задания
№1 Вычислить пределы
1.1)  .
.
Решение:


 =0;
=0;
1.2)  .
.
Решение:

 =0;
=0;
1.3)  при а1=1, а2=0, а3= 3, а4= -
при а1=1, а2=0, а3= 3, а4= -  .
.
Решение: 1.3.1  ;
;
1.3.2  ;
;


Можно вычислить предел частного двух многочленов из условия, что наибольшая степень дроби находится в знаменателе. Такой предел на бесконечности равен нулю.
Ответ: 1) 0,5; 2)  ; 3)
; 3) 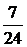 ; 4) 0.
; 4) 0.
№2 Найти область определения функции у=f(x),
 , построить её график.
, построить её график.
Исследовать функцию на непрерывность и определить вид её точек разрыва (вычислив каждый из частичных пределов).
Решение :
2.1) Значения функции f(x) можно вычислить при 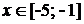 ,
,  ,
,  . Функция f(x) на каждом участке области определения задана (нет точек, в которых невозможно вычислить f(x) ), объединение всех участков даёт для функции f(x) область определения
. Функция f(x) на каждом участке области определения задана (нет точек, в которых невозможно вычислить f(x) ), объединение всех участков даёт для функции f(x) область определения  т.к.
т.к.  ;
;
2.2) Построим график функции, построив графики
·  при
при  ,
,
·  при
при  ,
,
· y3=1+2cos(2x) при  .
.

 График
График  – прямая, с угловым коэффициентом k=1 и сдвигом вниз относительно начала координат на b=3.
– прямая, с угловым коэффициентом k=1 и сдвигом вниз относительно начала координат на b=3.
Прямую можно построить и по двум точкам:
а) взять х1 и вычислить у(х1), например
при х= -5 у(-5)= -5 -3= -8;
б) взять х2 и вычислить у(х2), например
при х= -1 у(-1)= -1 -3= -4;
в) построить прямую по найденным точкам ( -5; -8) и (-1; -4).
График функции изобразим на промежутке  , на котором задана функция у1.
, на котором задана функция у1.
График функции  показан на рисунке 1.
показан на рисунке 1.

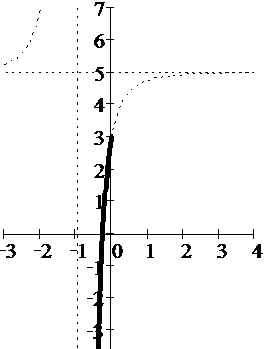 График
График  – гипербола, получаемая из
– гипербола, получаемая из  растяжением в 2 раза вдоль оси ОY вместе с переворотом относительно ОХ, сдвигом влево на 1 и вверх на 5 единиц.
растяжением в 2 раза вдоль оси ОY вместе с переворотом относительно ОХ, сдвигом влево на 1 и вверх на 5 единиц.
Функция 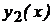 задана на интервале
задана на интервале  .
.
График  показан на рисунке 2.
показан на рисунке 2.
График  получается из графика
получается из графика  сжатием в 2 раза вдоль оси ОХ, растяжением в 2 раза вдоль оси ОY и сдвигом вверх на 1 единицу. График
сжатием в 2 раза вдоль оси ОХ, растяжением в 2 раза вдоль оси ОY и сдвигом вверх на 1 единицу. График 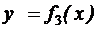 показан на рисунке 3.
показан на рисунке 3.
 Функция
Функция  задана на отрезке
задана на отрезке  .
.

2.3) Исследуем функцию f(x) на непрерывность.
Функция  задана на отрезке
задана на отрезке  . Функция
. Функция  является элементарной, из чего следует непрерывность такой функции в точках соответствующего интервала (-5; -1).
является элементарной, из чего следует непрерывность такой функции в точках соответствующего интервала (-5; -1).
Функция  задана на интервале
задана на интервале  , в его точках функция
, в его точках функция 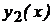 является элементарной, из чего следует непрерывность такой функции.
является элементарной, из чего следует непрерывность такой функции.
Функция y3=1+2·cos(2x) задана на отрезке  . Функция
. Функция  является элементарной, из чего следует непрерывность такой функции. в точках соответствующего интервала
является элементарной, из чего следует непрерывность такой функции. в точках соответствующего интервала  .
.
Вывод: Разрывы функции f(x) возможны только на границах участков области определения.
Рассмотрим каждую из границ области определения х1= -5, х2= -1, х3=0, х4=  .
.
2.3.1) х= -5,  .
.
Функция f(х) задана только при x  -5,
-5,
предел справа  существует, конечен и равен f(-5) т.е f(x) в точке х=-5 непрерывна справа;
существует, конечен и равен f(-5) т.е f(x) в точке х=-5 непрерывна справа;
2.3.2) х= -1, 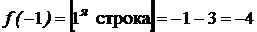 .
.
Предел слева  ,
,
предел справа  .
.
Среди частичных пределов в точке х= -1 имеется бесконечный, х= -1 является точкой разрыва второго рода;
2.3.3) х=0,  .
.
Предел слева 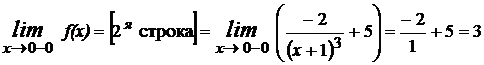 ,
,
предел справа  .
.
В точке х=0 частичные пределы совпадают и равны значению функции в такой точке, следовательно х=0 – точка непрерывности функции f(x);
2.3.4) х=  ,
,  .
.
Функция f(х) задана только при x  ,
,
предел слева  существует, конечен и равен f(
существует, конечен и равен f(  ) т.е f(x) в точке х=
) т.е f(x) в точке х=  непрерывна слева.
непрерывна слева.
С учётом выполненных пунктов построим график функции f(x).
График изображён на рисунке 4.
 |







 |
№3
3.1) Найти производную функции  .
.
Решение:
 =
=

Ответ:  .
.
3.2) Найти  , составить уравнения касательной и нормали
, составить уравнения касательной и нормали
при  для
для 
 ;
;
Решение:



 Уравнение нормали
Уравнение нормали  ,
,
 ,
,
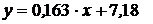 .
.
Уравнение касательной  ,
,
 ,
,
 .
.
 |
Ответ: При t=0  , касательная
, касательная  ,
,
нормаль 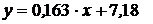 ;
;
3.3) Найти производную функции
а)  ; б)
; б)  .
.
Решение:
а)  .
.
Используем логарифмическое дифференцирование:

 ;
;
б)  .
.
Уравнение неявно задает функцию у=у(х), из него может быть найдена производная  . Продифференцируем обе части уравнения по переменной х, учитывая производную сложной функции
. Продифференцируем обе части уравнения по переменной х, учитывая производную сложной функции  . При этом получим уравнение
. При этом получим уравнение  .
.
Сгруппируем слагаемые, содержащие  и перенесём остальные слагаемые в правую часть равенства
и перенесём остальные слагаемые в правую часть равенства  ,
,
из чего получаем  .
.
Ответ: а)  ,
,
б)  .
.
3.4) Вычислить приближенно  .
.
Решение:
Пусть 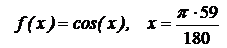 (перевели градусы в радианы).
(перевели градусы в радианы).
Для такой функции  .
.
Формула приближенных вычислений  .
.
( по первому приближению)
Возьмём  ,
,
тогда 
 .
.
( Калькулятор дает значение 0,515038074);
Ответ: 0,515.
3.5) Провести полное исследование функции и построить график
а)  ; б)
; б)  .
.
Решение:
а)  .
.
1) Область определения и область непрерывности :
Область определения функции  .
.
Область непрерывности совпадает с областью определения, т.к. y(x) является алгебраической функцией.
При х=1функция не определена,  ,
,
т.е. х=1 для функции является точкой разрыва второго рода;
2) Четность: 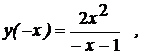
 Вывод: функция общего вида.
Вывод: функция общего вида.
Функция у(х) не периодическая;
3) Пересечение с осями и знаки функции:
а) с ОУ т.е. при х=0 у(0)=0 , пересечение с осью ОУ в точке (0; 0).
б) c осью ОХ т.е. находим решение уравнения у(х)=0,
 =0 при х=0, пересечение с осью ОХ в точке (0; 0);
=0 при х=0, пересечение с осью ОХ в точке (0; 0);
Располагая по возрастанию на числовой прямой точки пересечения графика с осью ОХ и точки, где у(х) не существует, получим три промежутка. Определим знак функции в точках каждого промежутка и получим

4) Асимптоты графика:
а) Вертикальные вида х=а (если хотя бы один частичный предел функции при
 бесконечен).
бесконечен).
При х=1 имеется бесконечный частичный предел
 (в данном случае оба)
(в данном случае оба)
и в других точках функция у(х) ограничена т.к. непрерывна.
Вертикальная асимптота х=1 (единственная);
б) Горизонтальные вида у=А (если предел функции при  существует,
существует,
конечен и равен А).
Пределы  оба бесконечные,
оба бесконечные,
горизонтальных асимптот нет;
в) Наклонные асимптоты , вида y1=k1×x+b1 и y2=k2×x+b2 .
Замечание: Если имеется правая (левая) горизонтальная асимптоты, то
соответствующая наклонная асимптоты можно не искать.
 совпадают,
совпадают,
 .
.
Правая и левая асимптота совпадают,
уравнение наклонной асимптоты у=2х+2;
5) Производная функции:

Промежутки монотонности функции:
Знаки производной на каждом промежутке можно определить непосредственной подстановкой значений х=  из каждого промежутка знакопостоянства производной (из области определения функции). Можно находить знак производной методом интервалов:
из каждого промежутка знакопостоянства производной (из области определения функции). Можно находить знак производной методом интервалов:
производная раскладывается на множители и при переходе через критическую точку  обращается внимание на чётность (нечётность) степени множителя
обращается внимание на чётность (нечётность) степени множителя  в выражении производной. Если степень
в выражении производной. Если степень  чётная, то знак производной при переходе через её критическую точку не изменяется, знак изменяется при нечётной степени .
чётная, то знак производной при переходе через её критическую точку не изменяется, знак изменяется при нечётной степени .
Разложив производную на множители, получим  .
.
Значения производной на самом правом промежутке ( х>2 ) положительные, имеют знак “ + “ т.к.  >0.
>0.
· При переходе через х=2 знак производной изменится на “ – “, т.к. множитель производной (х–2) участвует в нечётной (первой) степени;
· При переходе через х=1 знак производной не изменится, т.к. множитель производной (х –1) участвует в чётной (второй) степени;
· При переходе через х=0 знак производной изменится на “+“, т.к. множитель производной (х – 0) участвует в нечётной (первой) степени.

Вывод: функция возрастает при 
убывает при  ;
;
Точки экстремума:
1. х=0 является точкой экстремума, причём максимума, т.к. в ней функция
непрерывна и производная меняет знак с плюса на минус, у (0)=0;
2. х=1 не является точкой экстремума, т.к. в ней функция не определена;
3. х=2 является точкой экстремума, причём минимума, т.к. в ней функция
непрерывна и производная меняет знак с минуса на плюс, у (2) = 8;
6) Вторая производная:


Критические точки второй производной:

Промежутки выпуклости графика:
Определим знак второй производной на каждом промежутке её
знакопостоянства (из области определения функции) :
· Знак  на самом правом промежутке x>1 “+ “ т.к.
на самом правом промежутке x>1 “+ “ т.к.  т.е. на
т.е. на
· При переходе через х=1 знак производной изменится на “ – “, т.к. (х – 1) участвует во второй производной в нечётной (третьей) степени т.е
на таком промежутке график функции выпуклый (выпуклый вверх);

Точки перегиба:
а) х=1 не является точкой перегиба, т.к. в ней функция не задана и разрывная;
б) Других критических точек второй производной нет.
Точек перегиба нет;
6) Для построения графика функции возьмём несколько вспомогательных точек из области определения функции: у(-3)= -9, у(0,5)= -1, у(4)=10+2/3.
С учётом результатов всех пунктов плана получим график функции,
изображенный на рисунке 6.


№5.(б) Провести полное исследование функции 
и построить график.
Решение:
1) Область определения и область непрерывности:
Функция определена на всей числовой прямой  .
.
Функция является элементарной т.е. её область непрерывности совпадает с
областью определения. Точек разрыва нет;
2) Четность:
 ,
,  и
и  ,
,
функция общего вида.
Функция S(t) не периодическая;
3) Пересечение с осями:
а) с осью OS: при t=0  и точка пересечения (0; 0,4) ;
и точка пересечения (0; 0,4) ;
б) с осью ОТ:  , его решение t=3 и точка пересечения (3; 0);
, его решение t=3 и точка пересечения (3; 0);
Знаки функции

4) Асимптоты графика:
а) Вертикальных асимптот нет. т.к. функция на любом отрезке непрерывна,
следовательно, ограниченная;
б) Горизонтальные асимптоты

, левая горизонтальная асимптота S=0;
( ось ОТ )
 , правой горизонтальной асимптоты нет;
, правой горизонтальной асимптоты нет;
в) Наклонные
Слева (при  ) не ищем т.к. имеется горизонтальная асимптота.
) не ищем т.к. имеется горизонтальная асимптота.
Справа S=k×t+b,  .
.
Наклонных асимптот нет;
5) Производная  .
.
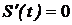 при t=2 и других критических точек производной нет.
при t=2 и других критических точек производной нет.
Знаки производной:

S ’(0)= 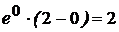 =1>0 ; S(2)=
=1>0 ; S(2)=  ; S ’(3)=
; S ’(3)=  <0.
<0.
7) Вторая производная:
 ,
,
a)  ;
;
б)  существует при любом t ,
существует при любом t ,
(других критических точек второй производной нет).
Знаки второй производной:
 |
 S’’(0)=
S’’(0)=  >0; S (1)=
>0; S (1)=  0,735; S”(3)=
0,735; S”(3)=  <0.
<0.
Точка t=1 является точкой перегиба графика функции;
8) График функции:
Для построения графика функции возьмём несколько вспомогательных
точек из области определения функции:
 ,
,
 .
.
С учётом результатов всех пунктов плана получим график, изображенный на рисунке 7.

|



 |
Справочник
Если  (бесконечно малая функция, БМ),
(бесконечно малая функция, БМ),
 (БМ),
(БМ),
 (бесконечно большая функция, ББ),
(бесконечно большая функция, ББ),
 (ББ),
(ББ),
 ,
,
то
1) При сравнении бесконечно малых вычисляется предел их частного и, в зависимости от результата

2) При сравнении бесконечно больших вычисляется предел их
частного и, в зависимости от результата
 .
.
3) При арифметических действиях без неопределённости
· с· (БМ с тем же порядком малости) | · (БМ с наименьшим из порядков малости слагаемых ) | · (БМ с порядком малости выше, чем у каждого из сомножителей) | ||||
| · с· (ББ с тем же порядком роста) | · (ББ с наибольшим из порядков роста слагаемых) | · с порядком роста выше, чем у каждого из сомножителей ) | ||||
| · | · | · | ||||
| · f(x) | · f(x)· |
| ||||
| · f(x) | · f(x)· |
| ||||
|
4) Виды неопределённостей в пределах: | ||||||
·  ; ;
| ·  ; ;
|
· |
· при одинаковом порядке роста | ·  .
с помощью 2го замечательного предела .
с помощью 2го замечательного предела
| ||
Основные эквивалентности в пределах:


 ,
,
 ,
,  ,
,
 ,
,  .
.
Если бесконечно малую (бесконечно большую) функцию в выражении заменить на эквивалентную, то предел выражения не изменится.
Шкала бесконечно больших функций:
при 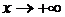
·  (a>1) (a>1)
| …..
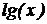

 ……
……
|
· 
| ….

 х
х

 ….
….
|
·  (a>1) (a>1)
| ….


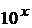 ….
….
|
| · n! (х! при | |
| · · ………….. | |
Стоящие ниже функции имеют большийпорядок роста.
Среди основных элементарных функций наименьший порядок роста имеет логарифмическая функция (с ростом её основания порядок роста уменьшается) и наибольший порядок роста имеет показательная функция (с ростом её основания порядок роста возрастает).
Виды точек разрыва:
·  − точка непрерывности для f(x);
− точка непрерывности для f(x);
·  − точка разрыва для f(x)
− точка разрыва для f(x)
нулевого рода (восполнимый разрыв);
· 
 − точка разрыва для f(x)
− точка разрыва для f(x)
первого рода (конечный скачок);
· Если хотя бы один из частичных пределов  и
и 
бесконечен, то 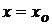 − точка разрыва второго рода (существенный разрыв).
− точка разрыва второго рода (существенный разрыв).
· Производная функции в точке 
 ;
;
· Геометрически  равна угловому коэффициенту касательной в соответствующей точке графика, в декартовых координатах
равна угловому коэффициенту касательной в соответствующей точке графика, в декартовых координатах  ,
,  – угол наклона касательной к графику функции в точке
– угол наклона касательной к графику функции в точке  ;
;
· Уравнение касательной 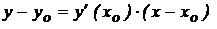 ;
;
· Уравнение нормали  ;
;
· Производная произведения  ;
;
· Производная дроби 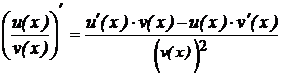 ;
;
· Логарифмическая производная  ,
,
 ;
;
· Дифференциал функции  ;
;
· Дифференциал второго порядка  ;
;
· Для функции, заданной параметрически 
производная у по х  ,
, 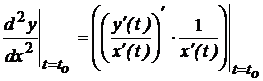 ;
;
· Формула Тейлора  ,
,
 ;
;
Таблица производных
| Функции | Производные | ||
| · | 
| ||
|
| c | 0 | |
| x | 1 | ||
|
| 
| ||
|
| 
| ||
|
| 
| ||
|
| 
| ||
| · |  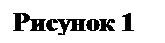
| ||
|
| 
| 
| |

| 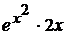
| ||

| 
| ||
| · | 
| ||
|
| 
| 
| |
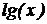
| 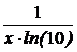
| ||
| | 
| ||
| | 
| ||
|
| 
| ||
| | 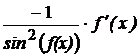
| ||
|
| 
| ||
|
| 
| ||
|
| 
| ||
|
| 
| ||
Для заметок:
4 Рекомендуемая литература
1) Шнейдер В.Е., Слуцкий А.И., Шумов А.С.
Краткий курс высшей математики (в 2х томах)
Т.1. – М.: Высшая школа, 2003. − 382 с.;
2) Пискунов Н.С.
Дифференциальное и интегральное исчисление для ВУЗов (в 2х томах)
Т.1 – М.: Интеграл-Пресс, 2000. – 416 с.;
3) Данко П.Е., Попов А.Г., Кожевникова Т.Я.
Высшая математика в примерах и задачах (в 2х частях)
Ч.1 – М.: Высшая школа, 1986 – 304 с.;
4) Задачи и упражнения по математическому анализу для ВТУЗов.
под ред. Демидовича Б.П. – М.: Наука, 1972. − 527 с.;
5) Шипачев В.С.
Высшая математика: Учебное пособие для ВУЗов.
– М.: Высшая школа, 1996. − 479 с.;
6) Запорожец Г.И.
Руководство к решению задач по математическому анализу
Изд. 4-е Учебное пособие для студентов ВТУЗов
− М: высшая школа, 1966. − 350 с.;
7) Власов В.Г. Конспект лекций по высшей математике.
– М.: Айрис, 1998 – 288с.;
8) Выгодский М.Я. Справочник по высшей математике. −
− М: Астрель:АСТ, 2002. −288 с.
Пределы. Непрерывность.
Производная функции одной переменной.
Учебно-методическое пособие по курсу «ВЫСШАЯ МАТЕМАТИКА»
для студентов всех специальностей всех форм обучения
Новоуральск, изд. НГТИ, 2004. − 60 с.
Макет подготовлен на кафедре ВМ НГТИ
Подписано в печать _______________ Формат А5 Гарнитура
Печать плоская. Усл-печ. л. ________ Тираж _______ экз. Заказ _______
Издательство Новоуральского Государственного Технологического Института,
624130, г. Новоуральск, ул. Ленина 85, НГТИ
Лицензия РФ ПЛР №00751 от 18.01.2000 г.
Дата добавления: 2018-04-15; просмотров: 425; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 0
0



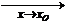
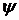
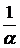





 ;
; ;
;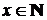 )
) x>1
x>1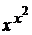 x>1
x>1








