Текст модуля с функцией newton
ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра «Информационно-вычислительные системы»
Отчет
о выполнении лабораторной работы №1
"Численные методы линейной алгебры.
Решение нелинейных уравнений и систем уравнений"
Выполнила: ст.гр.09ВО1
Голобокова М.А.
Проверил: В. И. Горбаченко
Пенза, 2011
Цель работы
Разработать программу для решения системы нелинейных уравнений методом Ньютона.
Задание
Вариант №24.
Методом Ньютона решить систему уравнений

с начальным приближением  . Исследовать влияние начального приближения на сходимость итерационного процесса.
. Исследовать влияние начального приближения на сходимость итерационного процесса.
Анализ задания
Задача ставится следующим образом: требуется найти решение системы  линейных алгебраических уравнений с
линейных алгебраических уравнений с  неизвестными:
неизвестными:

или в векторной форме

где
 ,
,
Вектор  определяет точку в n-мерном Евклидовом пространстве, т.е.
определяет точку в n-мерном Евклидовом пространстве, т.е. 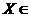 этому пространству и удовлетворяет всем уравнениям системы.
этому пространству и удовлетворяет всем уравнениям системы.
В отличие от систем линейных уравнений для систем нелинейных уравнений неизвестны прямые методы решения. При решении систем нелинейных уравнений используются итерационные методы. Эффективность всех итерационных методов зависит от выбора начального приближения (начальной точки), т.е. вектора  .
.
Выбор начальной точки  во многом определяется интуицией и опытом специалиста.
во многом определяется интуицией и опытом специалиста.
Так, например сходимость итерационной последовательности, получаемой в методе Ньютона, зависит от выбора начального приближения 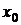 . Это можно заметить и из геометрической интерпретации метода. Так, если в качестве начального приближения взять точку
. Это можно заметить и из геометрической интерпретации метода. Так, если в качестве начального приближения взять точку 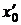 (рис. 1), то на сходимость итерационного процесса рассчитывать не приходится.
(рис. 1), то на сходимость итерационного процесса рассчитывать не приходится.
|
|
|
Если же в качестве начального приближения выбрать точку 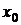 , то получим сходящуюся последовательность.
, то получим сходящуюся последовательность.
 |
В общем случае, если задан отрезок
 , содержащий корень, и известно, что функция
, содержащий корень, и известно, что функция 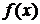 монотонна на этом отрезке, то в качестве начального приближения
монотонна на этом отрезке, то в качестве начального приближения 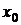 можно выбрать ту границу отрезка
можно выбрать ту границу отрезка  , где совпадают знаки функции
, где совпадают знаки функции 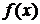 и второй производной
и второй производной  . Такой выбор начального приближения гарантирует сходимость метода Ньютона при условии монотонности функции на отрезке локализации корня.
. Такой выбор начального приближения гарантирует сходимость метода Ньютона при условии монотонности функции на отрезке локализации корня.
Для решения системы нелинейных уравнения в данной лабораторной работе используются метод Ньютона.
Главное преимущество итерационных методов решения в том, что погрешность решения не накапливается.
Метод Ньютона имеет квадратичную сходимость, т.е. в отличии от линейных задач погрешность на следующей итерации пропорциональна квадрату погрешности на предыдущей итерации. А так же быстрая сходимость метода Ньютона гарантируется лишь при очень хороших, т.е. близких к точному решению, начальных приближениях. Если начальное приближение выбрано неудачно, то метод может сходиться медленно, либо не сойдется вообще.
|
|
|
Описание метода решения
Метод Ньютона:
Задаем абсолютную или относительную погрешность  , вектор начальных приближений
, вектор начальных приближений  (с компонентами
(с компонентами 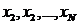 , где
, где  – количество уравнений).
– количество уравнений).
Используя разложение  в ряд Тейлора, формируем матрицу Якоби
в ряд Тейлора, формируем матрицу Якоби 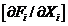 , необходимую для расчета приращений
, необходимую для расчета приращений  при малом изменении переменных. Матрица Якоби в развернутом виде записывается следующим образом:
при малом изменении переменных. Матрица Якоби в развернутом виде записывается следующим образом:

Составляем и решаем систему линейных уравнений для малых приращений  :
:
 .
.
Решение этой системы дает 
 , т.е.
, т.е.  .
.
Вычисляем уточненные значения

или в общем виде



Для максимального  проверяем одно из условий:
проверяем одно из условий:  .
.
Если оно выполняется, то выполняем новую итерацию. Иначе считаем вектор  найденным решением.
найденным решением.
Описание программы
Программа разрабатывается в системе MATLAB.
Входными данными являются допустимая погрешность и максимальное число итераций.
Выходными данными являются количество итераций, за которые получено решение(i для метода простых итераций и in для метода Ньютона), Погрешность решения (pog), решение системы (значения X и Y) и график сходимости.
|
|
|
Описание алгоритма:
Метод Ньютона:
1.вводим допустимую погрешность и максимальное число итераций
2.задаем начальное приближение
3.находим матрицу Якоби и матрицу функций
4.находим поправку решений
5.находим решение системы
6.определяем относительную норму поправки
7.если больше допустимой, то повторяем со второго пункта, принимая за начальное следующее значение, пока не достигнет максимально числа итераций
8.если меньше допустимой, то выходим из цикла.
9.выдаем результат на экран в виде графика и матрицы решения системы и относительную норму поправки.
Результаты выполнения программы lab1 представлены в приложении Б.
Описание применения
Чтобы запустить программу на выполнение, мы должны открыть файл LAB1.m, предварительно указав путь на папку с подпрограммами. Запустив выше указанный файл на выполнение, нам будет предложено ввести значение относительной погрешности решения и максимального числа итераций. После того, как мы укажем значения, следует нажать ввод. Программа выведет сообщение, которое будет содержать график и матрицу решения системы и относительную норму поправки.
|
|
|
Заключение
Данная программа позволяет найти решение системы нелинейных уравнений методом Ньютона. Полученные значения имеют погрешность ниже допустимой.
За 21 итераций получено приближение решения с относительной нормой поправки err=1.246545e-007
Значение вектор-функции в точке приближения решения равно
Y =
1.0e-009 *
0
-0.0081
-0.1637
0.0006
ПРИЛОЖЕНИЕ А
Текст главного модуля LAB1
% Пример решения системы нелинейных уравнений F(X)=0
% методом Ньютона
close all
clc
clear
% Вектор начального приближения
X0=[1;1;1;1];
disp('Решение системы нелинейных уравнений методом Ньютона');
epsilon=input('Введите допустимую ошибку вычислений epsilon=');
k_max=input('Введите максимально допустимое число итераций k_max=');
[X, err, k, Y,p]=newton('Fmat', 'Jmat', X0, epsilon, k_max)
if p==0
fprintf(1,'\nДопустимая ошибка %e не достигнута за %u итераций',epsilon,k_max);
else
fprintf(1,'\nЗа %u итераций получено приближение решения с относительной нормой поправки err=%e\n',k,err);
disp('Значение вектор-функции в точке приближения решения равно');
Y
end
Текст модуля с функцией newton
function [X, err, k, Y,p]=newton(F, J, X0, epsilon, k_max)
% Функция находит корень уравнения F(X)=0 методом Ньютона
% Входные параметры:
% F- имя вектор-функции, вводимое как строка,
% при этом функция должна быть записана
% в виде отдельной функции MATLAB;
% J-имя матрицы якоби вектор-функции F,
% якобиан должен быть записан
% в виде отдельной функции MATLAB;
% X0-вектор-столбец начального приближения;
% epsilon-допустимая ошибка вычисления корня (по относительной норме поправки решения);
% k_max-максимально допустимое число итераций.
% Выходные параметры:
% X-вектор решения системы уравнений;
% err-достигнутая ошибка вычисления корня (по относительной норме поправки решения);
% k-число итераций;
% Y-вектор значений вектор-функции F(X) в точке приближенного решения;
% p-признак достижения решения:
% p=1-решение получено, p=0-решение не получено.
p=0; % признак достижения решения
for k=1:k_max
% Поправка к решению
DX=feval(J,X0)\-feval(F,X0);
% Формирование решения
X = X0+DX;
Y=feval(F,X); % Вектор-функция в точке решения
norm_X=norm(X,inf);
norm_DX=norm(DX,inf);
err=norm_DX/norm_X; % Относительная норма поправки решения
dx(k) = err; % для графика
L(k) = k; % для графика
if err<=epsilon
p=1;
break;
else
X0=X;
end
end
if p==1
loglog(L, dx)
grid on
title('Метод Ньютона')% заголовок окна
xlabel('Число итераций') % надпись по оси X
ylabel('Относительная норма поправки')% надпись по оси Y
end
Дата добавления: 2018-04-15; просмотров: 197; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
