Точка пересечения прямой с плоскостью

Nbsp; МЕНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ   Автономная некоммерческая образовательная организация высшего образования «Сибирский институт бизнеса и информационных технологий»

ФАКУЛЬТЕТ ПРИКЛАДНОЙ ИНФОРМАТИКИ

Профиль: информационная безопасность

 

РЕФЕРАТ

На тему:

Уравнение плоскости и прямой в пространстве.Интеграция математических и экономических знаний.

 

 

Работу выполнил

студент 1 курса

заочного отделения

Федотов Максим Юрьевич

 

 

Омск-2018

Содержание

ФАКУЛЬТЕТ ПРИКЛАДНОЙ ИНФОРМАТИКИ.. 1

ВВЕДЕНИЕ. 3

1. ПЛОСКОСТЬ В ПРОСТРАНСТВЕ. 6

1.1.Точка пересечения прямой с плоскостью.. 6

1.2.Угол между прямой и плоскостью.. 7

2. ПРЯМАЯ В ПРОСТРАНСТВЕ. 10

2.1.Различные случаи положения прямой в пространстве. 11

2.2.Угол между прямой и плоскостью.. 14

ЗАКЛЮЧЕНИЕ. 23

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 26

 

 

ВВЕДЕНИЕ

Всякое уравнение первой степени относительно координат x, y, z

Ax + By + Cz +D = 0

задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением, которое называется уравнением плоскости.

Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении коэффициенты A, B, C одновременно не равны 0.

Особые случаи уравнения

1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A₁ x + B₁ y + C₁ z + D₁ = 0, A₂ x + B₂ y + C₂ z + D₂ = 0;

2) двумя своими точками M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), тогда прямая, через них проходящая, задается уравнениями:

= ;

3) точкой M₁(x₁, y₁, z₁), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

.

Уравнения называются каноническими уравнениями прямой.

Вектор a называется направляющим вектором прямой.

Параметрические уравнения прямой получим, приравняв каждое из отношений параметру t:

x = x₁ +mt, y = y₁ + nt, z = z₁ + рt.

Решая систему как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой:

x = mz + a, y = nz + b.

От уравнений можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:

.

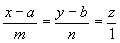От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [n₁, n₂], где n₁(A₁, B₁, C₁) и n₂(A₂, B₂, C₂) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система

равносильна системе ; такая прямая перпендикулярна к оси Ох.

Система равносильна системе x = x₁,y = y₁; прямая параллельна оси Oz.

 

ПЛОСКОСТЬ В ПРОСТРАНСТВЕ

Точка пересечения прямой с плоскостью

Пусть плоскость Q задана уравнением общего типа: Ax+By+Cz+D=0, а прямая L в параметрическом виде: x=x₁+mt, y=y₁+nt, z=z₁+pt, тогда чтобы найти точку пересечения прямой L и плоскости Q, нужно найти значение параметра t, при котором точка прямой будет лежать на плоскости. Подставив значение x, y, z, в уравнение плоскости и выразив t, получим

Значение t будет единственным, если прямая и плоскость не параллельны.

Условия параллельности и перпендикулярности прямой и плоскости

Рассмотрим прямую L: 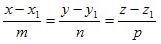и плоскость α: Ax+By+Cz+D=0.
Прямая L и плоскость α:

а) перпендикулярны друг другу тогда и только тогда, когда направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т. е.

б) параллельны друг другу тогда и только тогда, когда векторы и перпендикулярны, т. е.

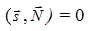и Am + Bn + Ср = 0.

---

Дата добавления: 2018-04-15; просмотров: 539; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!