Числовые характеристики дискретных случайных величин

Занятие 6. Дискретная случайная величина и ее числовые характеристики. Определение. Скалярную функцию Х(ω), заданную на пространстве элементарных исходов, называют случайной величиной, если для любого множество элементарных исходов, удовлетворяющих условию , является событием. Пример. На плоский экран падает частица. Будем считать, что нам известна вероятность попадания частицы в любое (измеримое, т.е. имеющее площадь) множество на экране. Случайными величинами в данном случае будут, например, расстояние X от центра экрана до точки падения, квадрат этого расстояния Y = X2, угол Z в полярной системе координат и т.д. Определение. Функцией распределения (вероятностей) случайной величины X называют функцию F(x), значение которой в точке х равно вероятности события {X < x}, т.е. события, состоящего из тех и только тех элементарных исходов ω, для которых : F(x) = P{X < x} Обычно говорят, что значение функции распределения в точке х равно вероятности того, что случайная величина X примет значение, меньшее х. Теорема. Функция распределения обладает следующими свойствами: 1) ; 2) F(x1) < F(x2) при x1 < x2 (т.е. F(x) − неубывающая функция); 3) , ; 4) ; 5) F(x) = F(x − 0), где − непрерывная слева функция).

Дискретные случайные величины

Определение. Случайную величину X называют дискретной, если множество ее возможных значений конечно или счетно.

X	x₁	x₂	...	x_i	...	x_n
P	p₁	p₂	...	p_i	...	p_n

Определение. Рядом распределения (вероятностей) дискретной случайной величины X называют таблицу, состоящую из двух строк: в верхней строке перечислены все возможные значения случайной величины, а в нижней − вероятности p_i = P{X = x_i} того, что случайная величина примет эти значения.

Таким образом, функция распределения дискретной случайной величины является кусочно постоянной функцией, принимающей на промежутке (−∞, х₁] значение 0, на промежутках (x_i, x_i ₊₁], 1 ≤ i <n, − значение р₁ + ... +p_i и на промежутке (x_n, +∞) − значение 1.

X	0	1	...	i	...	n
P			...	p_i	...	pⁿ

Биномиальное распределение. Дискретная случайная величина X распределена по биномиальному закону, если она принимает значения 0,1, 2,... , n в соответствии с распределением, заданным формулой

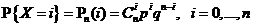
или, что тоже самое, рядом распределения, представленным в таблице, где 0<p, q <1 и p + q = 1.

X	0	1	2	...	n	...
P				...		...

Распределение Пуссона. Дискретная случайная величина X распределена по закону Пуассона, если она принимает целые неотрицательные значения с вероятностями

или, по-другому, с вероятностями, представленными рядом распределения в таблице, где λ > 0 − параметр распределения Пуассона.

Геометрическое распределение. Рассмотрим схему Бернулли.

X	0	1	2	...	n	...
P	p	qp	q²p	...	qⁿp	...

Пусть X − число испытаний, которое необходимо провести, прежде чем появится первый успех. Тогда X − дискретная случайная величина, принимающая значения 0, 1, 2, ..., n, ... Определим вероятность события {X = n}. Очевидно, что X = 0, если в первом же испытании произойдет успех.

Поэтому . Далее, X =1 в том случае, когда в первом испытании произошла неудача, а во втором − успех. Но вероятность такого события, равна qp, т.е. . Аналогично X = 2, если в первых двух испытаниях произошли неудачи, а в третьем − успех, и, значит, Продолжая эту процедуру, получаем

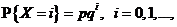
Случайную величину с таким рядом распределения называют распределенной согласно геометрическому закону.

Числовые характеристики дискретных случайных величин

Определение. Математическим ожиданием (средним значением) MX дискретной случайной величины X называют сумму произведений значений x_i случайной величины и вероятностей p_i = P{Х = x_i}, с которыми случайная величина принимает эти значения: . При этом, если множество возможных значений случайной величины X счетно, предполагается, что 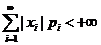, т.е. ряд, определяющий математическое ожидание, сходится абсолютно; в противном случае говорят, что математическое ожидание случайной величины X не существует.

Теорема. Математическое ожидание удовлетворяет следующим свойствам.

1. Если случайная величина X принимает всего одно значение С с вероятностью единица (т.е., по сути дела, не является случайной величиной), то МС = С.

2. М(аХ + b) = aMХ + b, где а, b − постоянные.

3. М(Х₁ + Х₂) = МХ₁ + МХ₂.

4. для независимых случайных величин Х₁ и Х₂.

Определение. Дисперсией DХ случайной величины X называют математическое ожидание квадрата отклонения случайной величины X от ее среднего значения, т.е.

Дисперсия дискретной случайной величины вычисляется по формуле

Теорема. Дисперсия удовлетворяет следующим свойствам.

1. Если случайная величина X принимает всего одно значение С с вероятностью единица, то DC = 0.

2. D(aX + b) = a²DX. 3. DX = MX² − (MX)².

4. D(X + Y) = DX + Dy для независимых случайных величин X и Y.

Нетрудно видеть, что дисперсия DX имеет размерность квадрата размерности случайной величины X. Для практических же целей удобно иметь величину, характеризующую разброс значений случайной величины вокруг ее математического ожидания, размерность которой совпадает с размерностью X. В качестве такой величины естественно использовать , которую называют средним квадратичным отклонением случайной величины X (иногда также стандартом, или стандартным отклонением).

Пример 1. Математическое ожидание и дисперсию случайной величины X, распределенной по биномиальному закону (число успехов в n испытаниях по схеме Бернулли с вероятностью успеха р):

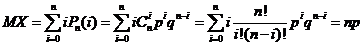
Можно посчитать по-другому. Представим число успехов X в n испытаниях по схеме Бернулли в виде

где Х_i − число успехов в i-м испытании. Нетрудно видеть, что

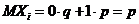Значит, в силу свойства 3 . Учитывая, что случайные величины Х_i являются независимыми, в силу свойства 4 дисперсии получаем .

Пример 2. Пусть случайная величина X имеет распределение Пуассона. Тогда

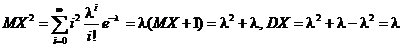
Пример 3. Пусть случайная величина X имеет геометрическое распределение:

Задачи. ОЛ−1 примеры 4.5, 4.6, МП−3 решение типовых примеров для задачи 7 ДЗ или ОЛ-3 примеры 18.265−18.268, 18.272, 18.278.

Пример 4.5. Игральную кость бросают один раз. Если выпадает четное число очков, игрок выигрывает 8 рублей, если нечетное, но больше одного − проигрывает 1 рубль, если выпадает одно очко − проигрывает 10 рублей. Найдем распределение случайной величины X − величины выигрыша в данной игре.

Пространство элементарных исходов в данном случае имеет вид

где − выпадение i очков. Считая, что игральная кость симметричная, имеем

Случайная величина X может принять всего три значения: , и (является дискретной), причем каждому из этих значений соответствуют события

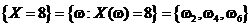
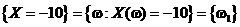
с вероятностями

Таким образом, ряд распределения случайной величины X можно представить в виде табл.

X	−10	−1	8
P	1/6	1/3	1/2

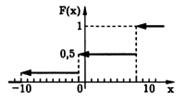
Найдем теперь функцию распределения F(x) случайной величины X. В соответствии с определением функции распределения

Пример 4.6. Производят четыре независимых опыта, в каждом из которых некоторое событие A появляется с вероятностью p = 0,8. Построим ряд распределения и функцию распределения случайной величины X − числа появлений события A в четырех опытах.

В соответствии с условием задачи мы имеем дело со схемой Бернулли, т.е. число появлений события А распределено по биномиальному закону с параметрами n = 4, p = 0,8 и q = 1 − p = 0,2. Значит, случайная величина X может принимать только значения i, i = 0, 1, 2, 3, 4. Согласно формуле Бернулли

определим вероятности возможных значений случайной величины X:

X	0	1	2	3	4
P	0,0016	0,0256	0,1536	0,4096	0,4096

Функция распределения случайной величины X имеет вид

18.265. Функция распределения случайной величины X дискретного типа имеет следующий вид:

Вычислить P(X ≥ 3,5} и P(|X| < 2,5}.

Ответ: P(X ≥ 3,5} = 1/2, P(|X| < 2,5} = 0,3.

18.266 (продолжение). Описать закон распределения случайной величины X из предыдущей задачи и найти т_х и D_x.

Ответ: m_X = 3,3, D_X = 0,76

x_i	2	3	4
	0,3	0,2	0,5

18.267. Два стрелка независимо друг от друга делают по одному выстрелу в мишень. Вероятность попадания в мишень дли первого стрелка р₁ для второго р₂. Случайная величина X − суммарное число попаданий в мишень в данном эксперименте. Описать закон распределения данной случайной величины и найти т_х и D_x.

Ответ: m_X = p₁ + p₂,3, D_X = p₁q₁ + p₂q₂

x_i	0	1	2
	q₁q₂	p₁q₂ + p₂q₁	p₁p₂

18.268. Один раз брошены три одинаковые игральные кости. Случайная величина X принимает значение 1, если хотя бы на одной игральной кости выпадет цифра шесть; принимает значение 0, если шестерка не выпала ни на одной грани, но хотя бы на одной из граней появилась цифра 5, и принимает значение −1 в остальных случаях. Описать закон распределения случайной величины X. вычислить функцию распределения и найти математическое ожидание и моду распределения.

Ответ: m_X = 1/8, d_X = 1.

x_i	−1	0	1
	8/27	61/216	91/216

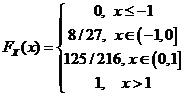
18.272. Производятся последовательные независимые испытания пяти приборов на надежность. Надежность каждого из приборов равна р. Каждый следующий прибор испытывается только в том случае, когда предыдущий оказался надежным. Описать закон распределения случайной величины X − числа испытанных в данном эксперименте приборов − и вычислить d_x и т_х.

Ответ: ,

x_i	1	2	3	4	5
	q	pq	p²q	p³q	p⁴

18.278. Из урны, содержащей 4 белых и 6 черных шаров, случайным образом и без возвращения извлекается 3 шара. Случайная величина X −число белых шаров в выборке. Описать закон распределения. Полученное распределение относится к семейству гипергеометрических.

x_i	0	1	2	3
	1/6	1/2	3/10	1/30

Домашнее задание. ОЛ−1 задачи 4.23−4.26, МП−3 задача 7 ДЗ, или ОЛ−3 задачи 18.275, 18.279, 18.280.

4.23. Из партии в 10 деталей, среди которых две бракованные, наудачу выбирают три детали. Найдите закон распределения числа бракованных деталей среди выбранных. Постройте функцию распределения. Ответ:

4.24. Вероятность приема самолетом радиосигнала при каждой передаче равна 0,7. Найдите ряд распределения и функцию распределения числа X принятых сигналов при шестикратной передаче.

Ответ: Ряд распределения и функцию распределения случайной величины X легко построить, зная, что , .

4.25. Найдите закон распределения случайной величины X − числа таких бросаний трех игральных костей, в каждом из которых ровно на двух костях появится по 2 очка, если общее число бросаний равно 15.

Ответ: , где .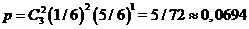

4.26. В течение часа на станцию скорой помощи поступает случайное число X вызовов, распределенное по закону Пуассона с параметром λ = 5. Найдите вероятность того, что в течение часа поступит: а) ровно два вызова; б) не более двух вызовов; в) не менее двух вызовов.

Ответ: а) P{Х = 2} = 5²е⁻⁵/2! ≈ 0,086;

б) P{Х ≤ 2} = (5⁰/0! + 5¹/1! + 5²/2!)е⁻⁵ ≈ 0,127;

в) P{X ≤ 2} = 1 − P{X < 2} = 1 − (5⁰/0! + 5¹/l!) е⁻⁵ ≈ 0,041.

18.275. Случайная величина X принимает только целые неотрицательные значения. Доказать, что .

Указание. Использовать соотношение, справедливое для С.В.Д.Т. P{х = x_k} = F_X(x_k ₊ ₁) − F_X(x_k), и преобразовать сумму, выражающую математическое ожидание.

18.279 (продолжение 18.278). Для случайной величины из предыдущей задачи найти т_х и D_x. Ответ: m_x = 6/5, D_x = 14/25.

18.280. Для сборки прибора требуется 4 однотипных детали. Всего имеется 10 деталей, из которых только 6 доброкачественные. Наудачу отбирают 5 деталей (одну деталь "про запас"). Найти вероятность того, что можно будет произвести сборку прибора. Ответ: 11/42.

Дата добавления: 2018-04-15; просмотров: 1883; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!