Задания для практической работы
Практическая работа № 6. Построение графика функции с помощью производной
Цель занятия.Отработать навыки построение графиков функций с помощью производной
Краткие теоретические сведения
При исследовании функций и построении их графиков целесообразно пользоваться следующей схемой.
1. Нахождение области определения функции.
2. Исследование функции на четность и нечетность.
3. Отыскание вертикальных асимптот.
4. Нахождение экстремумов и интервалов монотонности функции. Составление схемы.
5. Нахождение интервалов выпуклости и вогнутости и точек перегиба графика функции.
6. Нахождение точек пересечения графика функции с осями, интервалов знакопостоянства функции. Отыскание дополнительных точек для построения графика.
7. Построение графика функции.
Пример 1.Построить график функции с помощью производной первого порядка 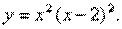
Решение.
1) Областью определения функции является вся числовая ось. То есть 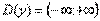
2) Функция ни четная, ни нечетная, так как 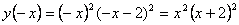 и
и 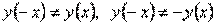
3) Найдём производную функции
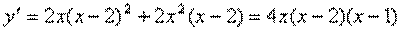 .
.
4) Найдём критические точки, в которых производная обращается в ноль 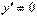
Это точки 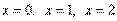
Отметим эти точки на числовой оси и определим знак производной на интервалах.
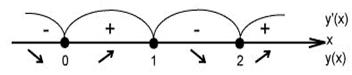
Таким образом: 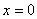 - точка минимума;
- точка минимума; 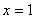 - точка максимума;
- точка максимума; 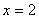 - точка минимума.
- точка минимума.
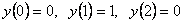 .
.
5) Строим график на основании проделанного исследования.
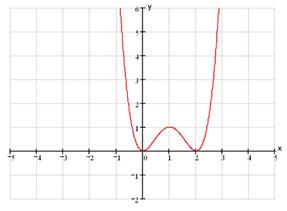 .
.
Пример 2. Провести полное исследование функции 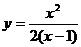 и построить ее график.
и построить ее график.
|
|
|
Решение.
1) Область определения функции – множество всех действительных чисел, исключая х=1. Т.о., 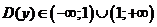 .
.
2) Функция не является четной, нечетной, периодической.
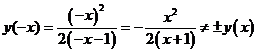
3) х=1 – разрыв второго рода
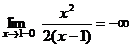 ,
, 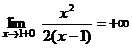 .
.
4) Исследуем функцию на монотонность, экстремумы.
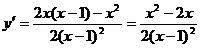 ; y¢=0 Û
; y¢=0 Û 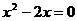 ,
, 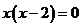
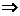 x1 = 0 или x2 =2.
x1 = 0 или x2 =2.
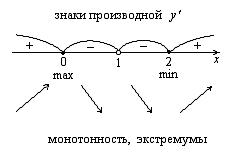 y¢ не существует в точке x = 1, но она не входит в область определения функции. Следовательно, имеются две критические точки x1 = 0 и x2= 2. Разобьем точками x1 = 0 и x2= 2, x = 1 область определения на интервалы знакопостоянства производной: (-¥; 0), (0; 1), (1; 2), (2; +¥). Определим знаки производной в этих интервалах: y¢(–1)>0 и y¢(3)>0 Þ в интервалах (-¥; 0) и (2; +¥) производная положительна, y¢(0,1)<0 и y¢(1,1)<0 Þ в интервалах (0; 1) и (1; 2) производная отрицательна (см. рис. 11). Используя достаточные условия монотонности и экстремума, получим следующие выводы: функция возрастает в интервалах (-¥; 0) и (2; +¥), убывает в (0; 1) и (1; 2), x = 0 – точка максимума, x = 2 – точка минимума. Значение максимума y(0)=0, значение минимума y(2)=2.
y¢ не существует в точке x = 1, но она не входит в область определения функции. Следовательно, имеются две критические точки x1 = 0 и x2= 2. Разобьем точками x1 = 0 и x2= 2, x = 1 область определения на интервалы знакопостоянства производной: (-¥; 0), (0; 1), (1; 2), (2; +¥). Определим знаки производной в этих интервалах: y¢(–1)>0 и y¢(3)>0 Þ в интервалах (-¥; 0) и (2; +¥) производная положительна, y¢(0,1)<0 и y¢(1,1)<0 Þ в интервалах (0; 1) и (1; 2) производная отрицательна (см. рис. 11). Используя достаточные условия монотонности и экстремума, получим следующие выводы: функция возрастает в интервалах (-¥; 0) и (2; +¥), убывает в (0; 1) и (1; 2), x = 0 – точка максимума, x = 2 – точка минимума. Значение максимума y(0)=0, значение минимума y(2)=2.
5) Исследуем функцию на направление выпуклости и точки перегиба.
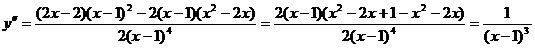 .
.
y² не обращается в 0, а в точке х = 1, где y² не существует, функция не определена, поэтому график функции не имеет точки перегиба. Таким образом, имеются два интервала (-¥; 1) и (1;+¥), знакопостоянства второй производной. y²(0)<0 Þ в интервале (-¥; 1) y² отрицательна, y²(2)>0 Þ в интервале (1; +¥) y² положительна . В силу достаточных условий выпукло
 |
сти и вогнутости графика в интервале (-¥; 1) график выпуклый (вверх), а в интервале (1; +¥) график вогнутый (выпуклый вниз).
|
|
|
6) Так как 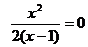 Ûx = 0, то график пересекает оси системы координат только в ее начале.
Ûx = 0, то график пересекает оси системы координат только в ее начале.
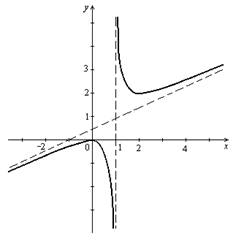
7) Начертим эскиз графика. Сначала начертим асимптоты x = 1 и 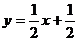 (на рисунке они начерчены пунктирной линией). Наносим на чертеж точки (0; 0) и (2; 2), найденные в пункте 4. Проводим через эти точки линию, согласно результатам исследования функции в пунктах 4, 5, 6. Еще раз сравниваем полученный график с результатами исследования, убеждаемся в правильности построения графика.
(на рисунке они начерчены пунктирной линией). Наносим на чертеж точки (0; 0) и (2; 2), найденные в пункте 4. Проводим через эти точки линию, согласно результатам исследования функции в пунктах 4, 5, 6. Еще раз сравниваем полученный график с результатами исследования, убеждаемся в правильности построения графика.
Задания для практической работы
Задание 1.Исследовать функцию, заданную формулой:
Задание 2. 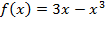
Задание 3. 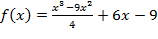
Задание 4.
Задание 5.
Задание 6. 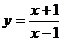
Задание 7. 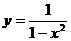
Задание 8. 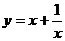 ;
;
Контрольные вопросы:
1. Сформулировать достаточное условие возрастания (убывания) функции на интервале.
2. Что такое экстремум функции?
|
|
|
3. Дайте определение экстремума функции.
4. Может ли функция иметь несколько экстремумов?
5. Сформулируйте теорему, выражающую необходимое условие экстремума.
6. Как вычислить наибольшее и наименьшее значения функции не интервале?
7. Как определить выпуклость и вогнутость графика функции?
8. Что такое точка перегиба?
9. Какова схема построения графика функции?
Дата добавления: 2018-04-04; просмотров: 995; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
