Зведені результати розрахунку миттєвих швидкостей руху
ПРАКТИЧНА РОБОТА №1
Розрахунок середньої швидкості руху транспортних засобів за результатами досліджень її миттєвих значень
Варіант – 4
Загальні відомості
Випадковою величиною називається змінна величина, значення якої залежать від випадкових обставин і для якої визначена функція розподілу ймовірностей. Дискретна випадкова величина – це випадкова величина, яка може набувати кінцеву або численну величину можливих значень. Математичним сподіванням (середнім значенням)  випадкової величини (у нашому випадку – миттєвої швидкості руху) називається положення випадкової величини на числовій осі. Для дискретної випадкової величини
випадкової величини (у нашому випадку – миттєвої швидкості руху) називається положення випадкової величини на числовій осі. Для дискретної випадкової величини  , що набуває можливі значення
, що набуває можливі значення  ,
,  , …,
, …,  ,… із ймовірностями (частостями)
,… із ймовірностями (частостями)  ,
,  ,…
,…  ,…, математичне сподівання визначається
,…, математичне сподівання визначається
 . (1.1)
. (1.1)
Частість визначається
 , (1.2)
, (1.2)
де п – об’єм вибірки; т – частота попадання значень миттєвих швидкостей у розряд.
Дисперсією випадкової величини називається математичне очікування квадрату відхилення величини від її математичного очікування. Дисперсіядискретної випадкової величини виражається формулою
 . (1.3)
. (1.3)
де  - середня швидкість ТЗ в інтервальному розподілі.
- середня швидкість ТЗ в інтервальному розподілі.
На практиці часто використовується інша числова характеристика випадкової величини – середнє квадратичне відхилення, що являє собою квадратний корінь з її дисперсії:
|
|
|
 . (1.4)
. (1.4)
Розмах вибірки значень швидкостей визначається
 . (1.5)
. (1.5)
Оцінка розподілу швидкостей руху транспортних засобів проводиться через визначення емпіричної та теоретичної густини. Емпірична густина визначається:
 , (1.6)
, (1.6)
де hі – ширина розряду розбиття швидкостей
Розподіл миттєвих швидкостей ТЗ підпорядковується, як правило, теоретичному нормальному закону розподілу з густиною
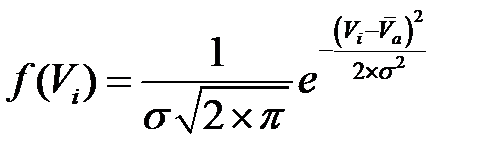 (1.7)
(1.7)
Для узгодження експериментального розподілу цьому теоретичному закону можна використати критерій згоди  - Пірсона
- Пірсона
 (1.8)
(1.8)
Для знаходження ймовірності згоди (за спеціальною таблицею математичної статистики) використовують ступені вільності
 (1.9)
(1.9)
де, 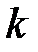 - кількість розрядів;
- кількість розрядів;
 - кількість параметрів закону розподілу.
- кількість параметрів закону розподілу.
Для підтвердження нормального закону розподілу використовується таблиця 1.2
Умова задачі
На перегоні міської вулиці за результатами натурного дослідження виявлено наступні швидкості руху поодиноких автомобілів: 42; 61; 65; 47; 54; 43; 66; 45; 53; 68; 44; 66; 52; 57; 53; 45; 55; 58; 52; 65; 54; 53; 72; 47; 47; 52; 47; 59; 61; 59; 61; 58; 41; 60; 71; 50; 53; 61; 51; 64; 52; 52; 38; 53; 53; 64; 78; 52; 42; 54; 45; 47; 43; 53; 55; 56; 44; 52; 67; 56; 75; 53; 47; 53; 76; 66; 61; 52; 73; 66; 43; 53; 64; 53; 47; 52; 53; 52; 46; 61; 67; 48;62; 57; 47; 63; 66; 75; 64; 39; 67; 66; 59; 65; 74; 56. Визначити числові характеристики розподілу дискретної випадкової величини – швидкості руху і за цими характеристиками побудувати гістограму та кумулянту інтервального розподілу швидкості.
|
|
|
Розв’язання задачі
На першому етапі об’єднуємо найбільш близькі за значенням величини у розряди, тобто виконуємо зведення (таблиця 1.1)
Інтервал розбиття Сшвидкості Vі вибирають залежно від точності вимірів, що вимагаються, діапазону її зміни від Vmax до Vmin.
 (1.10)
(1.10)
де, К – кількість розрядів, 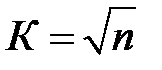 .
.
Таблиця 1.1
Зведені результати розрахунку миттєвих швидкостей руху
| Розряд швидкості, км/год | Середина інтервалу | Кількість потраплянь швидкостей у розряди | Частота mi, од | Частість, | Накопичення частоти F(V), % | Щільність | |||
Емпірична 
| Теоретична 
| ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 35…40 | 37,5 | ІІ | 2 | 2,08 | 2,08 | 0,000042 | 0,3170 | ||
| 40…45 | 42,5 | ІІІІІІІІ | 8 | 8,33 | 10,42 | 0,000167 | 0,1263 | ||
| 45…50 | 47,5 | ІІІІІІІІІІІІІ | 13 | 13,54 | 23,96 | 0,000271 | 0,0665 | ||
| 50…55 | 52,5 | ІІІІІІІІІІІІІІІІІІІІІІІІІІІ | 27 | 28,13 | 52,08 | 0,000563 | 0,0462 | ||
| 55…60 | 57,5 | ІІІІІІІІІІІІ | 12 | 12,50 | 64,58 | 0,000250 | 0,0423 | ||
| 60…65 | 62,5 | ІІІІІІІІІІІІІ | 13 | 13,54 | 78,13 | 0,000271 | 0,0512 | ||
| 65…70 | 67,5 | ІІІІІІІІІІІІІ | 13 | 13,54 | 91,67 | 0,000271 | 0,0819 | ||
| 70…75 | 72,5 | ІІІІ | 4 | 4,17 | 95,83 | 0,000081 | 0,1727 | ||
| 75…80 | 77,5 | ІІІІ | 4 | 4,17 | 100 | 0,000081 | 0,4808 | ||
|
| 96 | 100 | 100 | ||||||
Проведемо розрахунки:
- математичне сподівання швидкості руху становитиме:
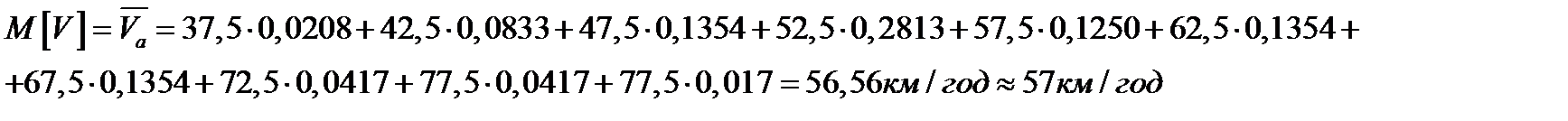 - величина розсіювання:
- величина розсіювання:

- дисперсія:

- середнє квадратичне відхилення: 
- коефіцієнт кореляції становитиме:

Таблиця 1.2
Значення критеріїв згоди  при перевірці підпорядкування експериментального розподілу нормальному закону
при перевірці підпорядкування експериментального розподілу нормальному закону
| r | p | |||||||||||||||
| 0,99 | 0,98 | 0,95 | 0,9 | 0,8 | 0,7 | 0,5 | 0,3 | 0,2 | 0,1 | 0,05 | 0,02 | 0,01 | 0,001 | |||
| 1 | 0,000 | 0,001 | 0,004 | 0,016 | 0,064 | 0,148 | 0,455 | 1,074 | 1,642 | 2,710 | 3,840 | 5,410 | 6,640 | 10,830 | ||
| 2 | 0,020 | 0,040 | 0,103 | 0,211 | 0,446 | 0,713 | 1,386 | 2,410 | 3,220 | 4,600 | 5,990 | 7,720 | 9,210 | 13,820 | ||
| 3 | 0,015 | 0,185 | 0,352 | 0,584 | 1,005 | 1,424 | 2,370 | 3,660 | 4,640 | 6,250 | 7,820 | 9,840 | 11,340 | 16,270 | ||
| 4 | 0,297 | 0,429 | 0,710 | 1,064 | 1,649 | 2,200 | 3,360 | 4,880 | 5,990 | 7,780 | 9,490 | 11,670 | 13,280 | 18,460 | ||
| 5
| 0,554 | 0,752 | 1,145 | 1,610 | 2,340 | 3,000 | 4,350 | 6,060 | 7,290 | 9,240 | 11,070 | 13,390 | 15,090 | 20,500 | ||
| 6 | 0,872 | 1,134 | 1,635 | 2,200 | 3,070 | 3,830 | 5,350 | 7,230 | 8,560 | 10,640 | 12,590 | 15,030 | 16,810 | 22,500 | ||
| 7 | 1,239 | 1,564 | 2,170 | 2,830 | 3,820 | 4,670 | 6,350 | 8,380 | 9,800 | 12,020 | 14,070 | 16,620 | 18,480 | 24,300 | ||
| 8 | 1,646 | 2,030 | 2,730 | 3,490 | 4,590 | 5,530 | 7,340 | 9,520 | 11,030 | 13,360 | 15,510 | 18,170 | 20,100 | 26,100 | ||
| 9 | 2,090 | 2,530 | 3,320 | 4,170 | 5,380 | 6,390 | 8,340 | 10,660 | 12,240 | 14,680 | 16,920 | 19,680 | 21,700 | 27,900 | ||
| 10 | 2,560 | 3,060 | 3,940 | 4,860 | 6,180 | 7,270 | 9,340 | 11,780 | 13,440 | 15,990 | 18,310 | 21,200 | 23,200 | 29,600 | ||
| 11 | 3,050 | 3,610 | 4,580 | 5,580 | 6,990 | 8,150 | 10,340 | 12,900 | 14,630 | 17,280 | 19,680 | 22,600 | 24,700 | 31,300 | ||
| 12 | 3,570 | 4,180 | 5,230 | 6,300 | 7,810 | 9,030 | 11,340 | 14,010 | 15,810 | 18,550 | 21,000 | 24,100 | 26,200 | 32,900 | ||
| 13 | 4,110 | 4,760 | 5,890 | 7,040 | 8,630 | 9,930 | 12,340 | 15,120 | 16,980 | 19,810 | 22,400 | 25,500 | 27,700 | 34,600 | ||
| 14 | 4,660 | 5,370 | 6,570 | 7,790 | 9,470 | 10,820 | 13,340 | 16,220 | 18,150 | 21,100 | 23,700 | 26,900 | 29,100 | 36,100 | ||
| 15 | 5,230 | 5,980 | 7,260 | 8,550 | 10,310 | 11,720 | 14,340 | 17,320 | 19,310 | 22,300 | 25,000 | 28,300 | 30,600 | 37,700 | ||
| 16 | 5,810 | 6,610 | 7,960 | 9,310 | 11,150 | 12,620 | 15,340 | 18,420 | 20,500 | 23,500 | 26,300 | 29,600 | 32,000 | 39,300 | ||
| 17 | 6,410 | 7,260 | 8,670 | 10,080 | 12,000 | 13,530 | 16,340 | 19,510 | 21,600 | 24,800 | 27,600 | 31,000 | 33,400 | 40,800 | ||
| 18 | 7,020 | 7,910 | 9,390 | 10,860 | 12,860 | 14,440 | 17,340 | 20,600 | 22,800 | 26,000 | 28,900 | 32,300 | 34,800 | 42,300 | ||
| 19 | 7,630 | 8,570 | 10,110 | 11,650 | 13,720 | 15,350 | 18,340 | 21,700 | 23,900 | 27,200 | 30,100 | 33,700 | 36,200 | 43,800 | ||
| 20 | 8,260 | 9,240 | 10,850 | 12,440 | 14,580 | 16,270 | 19,340 | 22,800 | 25,000 | 28,400 | 31,400 | 35,000 | 37,600 | 45,300 | ||
| 21 | 8,900 | 9,920 | 11,590 | 13,240 | 15,440 | 17,180 | 20,300 | 23,900 | 26,200 | 29,600 | 32,700 | 36,300 | 38,900 | 46,800 | ||
| 22 | 9,540 | 10,600 | 12,340 | 14,040 | 16,310 | 18,100 | 21,300 | 24,900 | 27,300 | 30,800 | 33,900 | 37,700 | 40,300 | 48,300 | ||
| 23 | 10,200 | 11,290 | 13,090 | 14,850 | 17,190 | 19,030 | 22,300 | 26,000 | 28,400 | 32,000 | 35,200 | 39,000 | 41,600 | 49,700 | ||
| 24 | 10,860 | 11,990 | 13,850 | 15,660 | 18,060 | 19,940 | 23,300 | 27,100 | 29,600 | 33,200 | 36,400 | 40,300 | 43,000 | 51,200 | ||
| 25 | 11,520 | 12,700 | 14,610 | 16,470 | 18,940 | 20,900 | 24,300 | 28,200 | 30,700 | 34,400 | 37,700 | 41,700 | 44,300 | 52,600 | ||
| 26 | 12,200 | 13,410 | 15,380 | 17,290 | 19,820 | 21,800 | 25,300 | 29,200 | 31,800 | 35,600 | 38,900 | 42,900 | 45,600 | 54,100 | ||
| 27 | 12,880 | 14,120 | 16,150 | 18,110 | 20,700 | 22,700 | 26,300 | 30,300 | 32,900 | 36,700 | 40,100 | 44,100 | 47,000 | 55,500 | ||
| 28 | 13,560 | 14,850 | 16,930 | 18,940 | 21,600 | 23,600 | 27,300 | 31,400 | 34,000 | 37,900 | 41,300 | 45,400 | 48,300 | 56,900 | ||
| 29 | 14,260 | 15,570 | 17,710 | 19,770 | 22,500 | 24,600 | 28,300 | 32,500 | 35,100 | 39,100 | 42,600 | 46,700 | 49,600 | 58,300 | ||
| 30 | 14,950 | 16,310 | 18,490 | 20,600 | 23,400 | 25,500 | 29,300 | 33,500 | 36,200 | 40,300 | 43,800 | 48,000 | 50,900 | 59,700 | ||
Для графічного зображення розподілу випадкової величини використовують гістограму для ряду відносних частот (частості) – полігон та криву розподілу (рис. 1.1), для ряду накопичуваних частот - кумулянту (рис. 1.2).

Рис. 1.1. Гістограма розподілу швидкостей руху ТЗ

Рис. 1.2. Кумулянта інтервального розподілу швидкості
Підставляючи у формулу 1.7 значення середніх інтервалів, визначаємо значення теоретичної густини для приблизного розподілу:
- для 1 інтервалу –  ;
;
- для 2 інтервалу –  ;
;
- для 3 інтервалу –  ;
;
- для 4 інтервалу –  ;
;
- для 5 інтервалу –  ;
;
- для 6 інтервалу –  ;
;
- для 7 інтервалу –  ;
;
- для 8 інтервалу –  ;
;
- для 9 інтервалу – 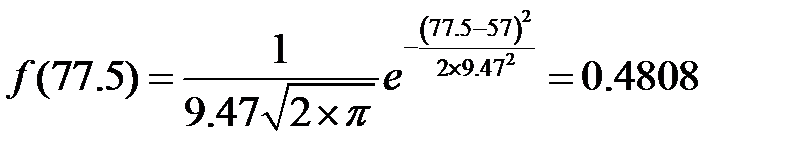 .
.
За формулами 1.8 та 1.9 розрахуємо критерій згоди та кількість ступеней вільності.

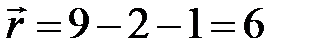 (
(  ,
,  , оскільки нормальний закон двопараметричний (
, оскільки нормальний закон двопараметричний (  і
і 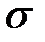 ))
))
Відповідь:  ;
;  ;
;  ;
;  ;
;  .
.
Виходячи із таблиці 1.2 для  і
і  , випливає, що значення
, випливає, що значення  відповідає величині ймовірності
відповідає величині ймовірності  . Ця ймовірність підтверджує гіпотезу щодо нормального закону розподілу швидкостей.
. Ця ймовірність підтверджує гіпотезу щодо нормального закону розподілу швидкостей.
Індивідуальне завдання
Дата добавления: 2018-04-05; просмотров: 225; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 , %
, % mi
mi