Побудова семантичного терму програми
Програма мови SIPL може бути перетворена в семантичний терм (терм програмної алгебри), який задає семантику цієї програми (семантичну функцію програми), перетвореннями такого типу:
· sem_P: Prog ® FS
· sem_S: Stm ® FS
· sem_A: Aexp ® FA
· sem_B: Bexp ® FB
Ці перетворення задаються рекурсивно (за структурою програми). Тому побудова семантичного терму залежить від вибору структури синтаксичного запису програми. Тут треба зважати на неоднозначність обраної нами граматики, що може призвести до різної семантики програм. Для досягненя однозначності треба користуватись пріоритетами операцій та типом їх асоціативності.
Таблиця 1.3
| Правило заміни | Назва правила |
|
sem_P: Prog ® FS задається правилами:
| |
| sem_P(beginSend)= sem_S(S) | NS_Prog |
|
sem_S: Stm ® FS задається правилами:
| |
| sem_S(x:=a)=ASx(sem_A(a)) sem_S(S1;S2)= sem_S(S1) ·sem_S(S2) sem_S(ifbthenS1elseS2)= IF(sem_B(b), sem_S(S1), sem_S(S2)) sem_S(whilebdoS)= WH(sem_B(b), sem_S(S)) sem_S(beginSend)=(sem_S(S)) sem_S(skip)=id | NS_Stm_As NS_Stm_Seq NS_Stm_If NS_Stm_Wh NS_Stm_Op NS_Stm_skip |
|
sem_A: Aexp ® FA задається правилами:
| |
sem_A(n)=  sem_A(a)=aÞ
sem_A(a1+a2)=S2(add, sem_A(a1), sem_A(a2))
sem_A(a1–a2)=S2(sub, sem_A(a1), sem_A(a2))
sem_A(a1*a2)=S2(mult, sem_A(a1), sem_A(a2))
sem_A(a1¸a2)=S2(div, sem_A(a1), sem_A(a2))
sem_A((a))=sem_A(a)
sem_A(a)=aÞ
sem_A(a1+a2)=S2(add, sem_A(a1), sem_A(a2))
sem_A(a1–a2)=S2(sub, sem_A(a1), sem_A(a2))
sem_A(a1*a2)=S2(mult, sem_A(a1), sem_A(a2))
sem_A(a1¸a2)=S2(div, sem_A(a1), sem_A(a2))
sem_A((a))=sem_A(a)
| NS_A_Num NS_A_Var NS_A_Add NS_A_Sub NS_A_Mult NS_A_Div NS_A_Par |
|
sem_B: Bexp ® FB задається правилами:
| |
sem_B(true)=  sem_B(false)=
sem_B(false)=  sem_B(a1<a2)=S2(less, sem_A(a1), sem_A(a2))
sem_B(a1£a2)=S2(leq, sem_A(a1), sem_A(a2))
sem_B(a1=a2)=S2(eq, sem_A(a1), sem_A(a2))
sem_B(a1¹a2)=S2(neq, sem_A(a1), sem_A(a2))
sem_B(a1³a2)=S2(geq, sem_A(a1), sem_A(a2))
sem_B(a1>a2)=S2(gr, sem_A(a1), sem_A(a2))
sem_B(b1Úb2)=S2(or, sem_B(b1), sem_B(b2))
sem_B(b1Ùb2)=S2(and, sem_B(b1), sem_B(b2))
sem_B(Øb)=S1(neg, sem_B(b))
sem_B((b))= sem_B(b)
sem_B(a1<a2)=S2(less, sem_A(a1), sem_A(a2))
sem_B(a1£a2)=S2(leq, sem_A(a1), sem_A(a2))
sem_B(a1=a2)=S2(eq, sem_A(a1), sem_A(a2))
sem_B(a1¹a2)=S2(neq, sem_A(a1), sem_A(a2))
sem_B(a1³a2)=S2(geq, sem_A(a1), sem_A(a2))
sem_B(a1>a2)=S2(gr, sem_A(a1), sem_A(a2))
sem_B(b1Úb2)=S2(or, sem_B(b1), sem_B(b2))
sem_B(b1Ùb2)=S2(and, sem_B(b1), sem_B(b2))
sem_B(Øb)=S1(neg, sem_B(b))
sem_B((b))= sem_B(b)
| NS_B_true NS_B_false NS_B_less NS_B_leq NS_B_eq NS_B_neq NS_B_geq NS_B_gr NS_B_or NS_B_and NS_B_neg NS_B_Par |
|
|
|
Наведені правила слід розглядати як загальні правила, які в логіці називають схемами правил. Щоб із загального правила (метаправила) отримати конкретне правило (об’єктне правило), слід замість синтаксичних метасимволів, таких як a, b, S, P, n, x, підставити конкретні синтаксичні елементи (записи), наприклад замість a підставити N–M, замість b – M>N і т.п. Далі ліва частина конкретного правила заміняються на його праву частину і т.д.
Доведення коректності програм
Доведення коректності програм можна проводити різними способами, зокрема – див. розділ 5: аксіоматична семантика. Головна задача – показати часткову та/або тотальну коректність програми, тобто що вона на довільних вхідних даних видає правильні, заздалегідь очікувані, результати (такі, що відповідають початковій формальній специфікації програми). Одним з підходів до доведення часткової коректності програм у композиційній семантиці є обчислення значення семантичного терму програми над деяким узагальненим даним d, що має вигляд пар ім’я – значення без конкретизації фіксованих значень змінних, тобто sem_P(P) (d), та порівняння отриманого даного (точніше – окремих його компонент-значень змінних) з очікуваним згідно формальної специфікації. Тотальна коректність доводиться шляхом доведення завершуваності програми. Останнє найчастіше зводиться до доведення завершуваності циклів, що входять до програми.
|
|
|
Розв’язки типових задач
Завдання 1.1. За допомогою алгоритму Евкліда знайти найбільший спільний дільник двох чисел GCD(M,N). Виконати:
1) побудувати програму для розв’язання задачі на мові SIPL,
2) побудувати дерево синтаксичного виводу програми,
3) побудувати композиційний семантичний терм програми,
4) обчислити значення семантичного терму над вхідним даним
[M->15,N->9].
Розв’язок.
Алгоритм Евкліда для пошуку найбільшого спільного дільника двох чисел є наступним:
1) Вхід : цілі числа m і n.
2) Якщо m=n то GCD(m,n)=m=n. Якщо m≠n то
3) Якщо m>n то покласти m=m–n , інакше покласти n=n–m .Далі дивитись п.2.
Cуть алгоритму полягає у наступному. Нехай GCD(m,n) – функція, що повертає найбільший спільний дільник чисел m і n. Якщо m = n, то GCD(m,n) = m = n. Якщо m > n то GCD(m,n) = GCD(m-n, n), якщо n > m то GCD(m,n) = GCD(m,n-m). Доведемо це.
|
|
|
Нехай GCD(m,n) = p, тоді m ділиться на p та n ділиться на p, відповідно, m – n і n – m також діляться на p. Отже, GCD(m-n, n) і GCD (m, n-m) діляться на GCD(m, n). Нехай q = GCD(m-n, n). Тоді маємо, що існують такі цілі t1 і t2, що m-n = t1q, n = t2q тоді m = m – n + n = t1q + t2q = (t1+t2)q, GCD(m,n) ділиться на q. З того, що p ділиться на q та q ділиться на p отримаємо, що p = q.
1) Алгоритм Евкліда обчислення найбільшого спільного дільника мовою SIPL матиме наступну нотацію:
GCD =
begin
while M ≠ N do
if M > N then M:= M – N else N:= N - M
end
2) Побудуємо дерево синтаксичного виводу наведеної програми згідно правил БНФ з таблиці 1.1, які задають мову SIPL.
За правилом NP1 БНФ мови SIPL бачимо, що нетермінал <програма> представляється у вигляді <програма> ::= begin <оператор> end.
Отже, на 1-ому кроці дерево виводу буде мати такий вигляд:

На другому кроці розпишемо нетермінал <оператор>. Виходячи з коду нашої програми, наш нетермінал <оператор> має саме такий вигляд:
<оператор> ::= while <умова> do <оператор> (правило NS4)
Отже, на другому кроці дерево виводу буде мати такий вид:

Далі розпишемо нетермінал <умова>.В нашому випадку <умова> ::= <вираз> ¹ <вираз> (правило NB4)

Тут кожен <вираз> представляється у вигляді <вираз>::=<змінна> (правило NA2), де в першому випадку<змінна>::= M, а в другому <змінна>::=N.
|
|
|
Отже, дерево синтаксичного виводу на наступному кроці має такий
вигляд:

Тепер розпишемо другу частину оператора while.
Виходячи з коду програми, цей нетермінал має такий вигляд: <оператор> ::= if <умова> then <оператор> else <оператор> (правило NS3) , де умова оператора if: <умова> ::= <вираз> > <вираз> (правило NS7), де кожен з виразів представлений змінною М та N відповідно.
Отже, дерево виводу на наступному кроці буде мати такий вигляд:

Далі залишилось розписати 2 оператора. Перший виконується тоді, коли умова оператора if істинна, другий – коли хибна.
Неважко переконатись, що в першому випадку на дереві виводу <оператор> буде мати такий вид:

А в другому випадку:

Отже, остаточно дерево синтаксичного виводу для нашої програми буде мати наступний вигляд:

Для перевірки коректності побудови дерева треба обійти його зліва направо, записуючи усі термінали (ті вирази, що записані без кутових дужок). В результаті має бути отриманий вихідний текст програми на мові SIPL.
3) Композиційний семантичний терм визначимо згідно структури програми за деревом виводу. Використовувати будемо правила його побудови в мові SIPL, що задані в таблиці 1.3.
Sem_P(GCD) = sem_P(begin while M≠N do if M>N then M:=M-N else N:=N-M end) = |застосовуємо правило NS_Prog | = sem_S(while M≠N do if M>N then M:=M-N else N:=N-M) = | застосовуємо правило NS_Stm_Wh| = WH(sem_B(M≠N), sem_S(if M>N then M:=M-N else N:=N-M)) = |для умови циклу застосовуємо правило NS_B_neq, а для тіла NS_Stm_If| = WH(S2(neq,sem_A(M), sem_A(N)), IF(sem_B(M>N), sem_S(M:=M-N), sem_S(N:=N-M))) = |для кожної зі змінних M і N в умові циклу застосовуємо правило NS_A_Var, для умови умовного оператора правило NS_B_gr, адля обох його операторів NS_Stm_As | = WH(S2(neq, M=>, N=>)), IF(S2(gr, sem_A(M), sem_A(N)),ASM(sem_A(M-N)), ASN(sem_A(N-M)))) = |для кожної зі змінних M і N в умові умовного оператора застосовуємо правило NS_A_Var, для інших двох його операторів NS_A_Sub| = WH( S2(neq, M=>, N=>), IF(S2(gr, M=>, N=>), ASM(S2(sub, sem_A(M), sem_A(N))), ASN(S2(sub, sem_A(N), sem_A(M))))) = |для кожної зі змінних M і N в двічі застосовуємо правило NS_A_Var| = WH( S2(neq, M=>, N=>), IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>))))
4) Процес обчислення значення задається формулами таблиці 1.2. Щоб їх застосовувати, треба робити конкретизацію загальних правил до конкретного стану. Отже, завдання полягає в отриманні значення аплікації – застосування функції, що задається нашим термом, до конкретного даного.
Отже, обчислимо Sem_P(GCD) ([M->15,N->9]) = WH( S2(neq, M=>, N=>), IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>))))([M->15,N->9])
Правила для обчислення циклу AF_WH говорять про необхідність поступового обчислення станів st0, st1, … і виконання тіла циклу (оператора fs) до тих пір, поки умова fb є істинною. Обчислимо значення умови циклу S2(neq, M=>, N=>) ([M->15,N->9]) = neq(15,9) = true, тому виконуємо тіло циклу із композицією початкового циклу:
IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>))) ° WH(…, …) ([M->15,N->9]) = WH(…, …) ( IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>))) ([M->15,N->9]) ) = | обчислимо значення умови оператора IF: S2(gr, M=>, N=>) ([M->15,N->9]) = gr(15,9) = true, тому виконуємо перший з двох операторів IF | = WH(…, …) ( ASM(S2(sub, M=>, N=>)) ([M->15,N->9]) ) = | обчислимо його, розписуючи присвоєння, віднімання та розіменування: ASM(S2(sub, M=>, N=>)) ([M->15,N->9]) = [M->15,N->9] Ñ [M->S2(sub, M=>, N=>) ([M->15,N->9])] = [M->15,N->9] Ñ [M->sub(15,9)] = [M->15,N->9]Ñ[M->6] = [M->6,N->9]. Отже, ми виконали першу ітерацію циклу. Далі за аналогією:
WH( S2(neq, M=>, N=>), IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>)))) ( [M->6, N->9] ) = | S2(neq, M=>, N=>) ([M->6,N->9]) = neq(6,9) = true | = IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>))) ° WH(…, …) ([M->6,N->9]) = WH(…, …) ( IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>))) ([M->6,N->9]) ) = | S2(gr, M=>, N=>) ([M->6,N->9]) = gr(6,9) = false | = WH(…, …) (ASN(S2(sub, N=>, M=>)) ([M->6,N->9]) ) = | обчислимо ASN(S2(sub, N=>, M=>)) ([M->6,N->9]) = [M->6,N->9] Ñ [N->S2(sub, N=>, M=>) ([M->6,N->9])] = [M->6,N->9] Ñ [N-> sub(9,6)] = [M->6,N->9] Ñ [N->3] = [M->6,N->3] | = WH( S2(neq, M=>, N=>), IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>)))) ( [M->6, N->3] ) = | S2(neq, M=>, N=>) ([M->6,N->3]) = neq(6,3) = true | = IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>))) ° WH(…, …) ( [M->6, N->3] ) = WH(…, …) ( IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>))) ([M->6,N->3]) ) = | S2(gr, M=>, N=>) ([M->6,N->3]) = gr(6,3) = true | = WH(…, …) ( ASM(S2(sub, M=>, N=>)) ([M->6,N->3]) ) = | обчислимо ASM(S2(sub, M=>, N=>)) ([M->6,N->3]) = [M->6,N->3] Ñ [M->S2(sub, M=>, N=>) ([M->6,N->3])] = [M->6,N->3] Ñ [M->sub(6,3)] = [M->6,N->3]Ñ[M->3] = [M->3, N->3] | = WH( S2(neq, M=>, N=>), IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>)))) ( [M->3, N->3] ) = | Значення умови циклу S2(neq, M=>, N=>) ([M->3,N->3]) = neq(3,3) = false, тому зупиняємо обчислення із поточним результатом | = [M->3, N->3].
Отже, Sem_P(GCD) ([M->15,N->9]) = [M->3, N->3].
Для зручності та скорочення можна перепозначати оператори і стани, що виникають в процесі обчислення, наприклад: F0 := WH( S2(neq, M=>, N=>), IF(S2(gr, M=>, N=>), ASM(S2(sub, M=>, N=>)), ASN(S2(sub, N=>, M=>)))) або d0 := [M->15,N->9]. Тоді умову можна переписати таким чином: знайти F0(d0), і продовжувати обчислення. Оскільки треба ретельно слідкувати за даними та їх зміною, тому краще записувати їх в окремій таблиці.
Завдання 1.2
Нехай в мові введена функція додавання одиниці Inc(x) але відсутня операція +. Розробити програму, яка обчислює результат додавання res двох невід‘ємних цілих чисел a та b.
1) побудувати програму для розв’язку задачі на мові SIPL,
2) побудувати дерево синтаксичного виводу програми,
3) побудувати композиційний семантичний терм програми,
4) довести коректність програми.
Розв’язок.
1) Програма для розв’язку задачі:
begin
r:= а;
і:= 0;
while i < b do
begin
r:= Inc(r);
i:= Inc(i)
end
end
begin[S2]
r:= а;
while b>0 do
begin
r:= Inc(rez);
b:= Dec(b)
end
end
2) Дерево синтаксичного виводу програми:
Першим кроком розпишемо нетермінал <програма>
<програма> ::= begin <оператор> end.
Отже, дерево синтаксичного виводу на 1-му кроці має такий вигляд:
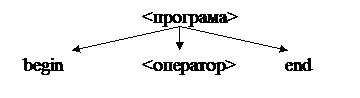
Далі необхідно розписати мета змінну <оператор>. Цей нетермінал представляється у вигляді:
<оператор> ::= <змінна>:=<вираз> | <оператор> ; <оператор>|
if<умова> then <оператор> else <оператор> |
while <умова> do <оператор> |
begin <оператор> end | skip
Виходячи з коду програми на другому кроці дерево виводу буде мати вигляд:
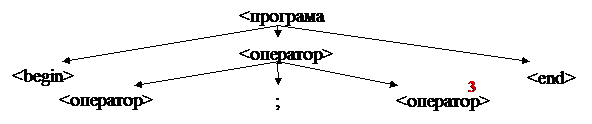
Розписуючи за правилом, наведеним вище, дерево виводу на третьому кроці буде розписане таким чином
 |
Далі нам доведеться розписати такі метазмінні, як <умова>, <змінна> та <вираз>. Згідно синтаксису мови SIPL ці нетермінали представляються таким чином:
<вираз> ::= <число> | <змінна> | <вираз> + <вираз> | <вираз> – <вираз> |
<вираз> * <вираз> | <вираз> ÷ <вираз> | (<вираз>)
<умова> ::= true | false | <вираз> < <вираз> | <вираз> £ <вираз> |
<вираз> = <вираз> | <вираз> ¹ <вираз> | <вираз> > <вираз> |
<вираз> ³ <вираз> | <умова> Ú <умова> | <умова> Ù <умова> |
Ø <умова> | (<умова>)
 Продовжуючи цей процес, отримаємо остаточний вигляд дерева:
Продовжуючи цей процес, отримаємо остаточний вигляд дерева:

3) Семантичний композиційний терм отримаємо без деталізації всіх кроків перетворень:
sem_P(Program) = sem_S(res:= a) • sem_S(i:= 0) • sem_S(while i < b do begin res:= res+1; i:= i+1 end) = ASres(a=>) • ASi(  ) • WH(S2(less, sem_A(i), sem_A(b)), sem_S(res:= res+1; i:= i+1)) =
) • WH(S2(less, sem_A(i), sem_A(b)), sem_S(res:= res+1; i:= i+1)) =
=ASres(a=>) • ASi(  ) • WH(S2(less,i=>, b=>), ASres(S2(add, res=>,
) • WH(S2(less,i=>, b=>), ASres(S2(add, res=>,  )) • ASi(S2(add, i=>,
)) • ASi(S2(add, i=>,  )))
)))
4) Доведення коректності програми
Доведення часткової коректності:
Композиційні терми для відмічених в дереві виводу операторів (з 1 по 5) будемо позначати відповідно f1, f2, f3, f4, та f5. Нехай d = [a→  , b→
, b→  ], тоді:
], тоді:
sem_P(Program)(d) = f1 • f2 • f3(d) = f3(f2 (f1(d))) = f3(f2 (d Ñ [res→a(d)])) = f3(f2 (d Ñ [res→  ])) = f3(f2 (d1)) = | d1 = [a→
])) = f3(f2 (d1)) = | d1 = [a→  , b→
, b→  , res→
, res→  ] | = f3(d1Ñ [i→0]) =
] | = f3(d1Ñ [i→0]) =
= f3(d2) = | d2 = [a→  , b→
, b→  , res→
, res→  , i→0] | = =
, i→0] | = = 
Позначимо G=WH(S2(less,i=>,b=>), ASres(S2(add, res=>,  )) •ASi(S2(add, i=>,
)) •ASi(S2(add, i=>,  ))).
))).
Нехай маємо dw = [a→  , b→
, b→  , res→
, res→  , i→0], тоді висунемо гіпотезу:
, i→0], тоді висунемо гіпотезу:
Гіпотеза: при виконанні n кроків тіла циклу G(dw) = [a→  , b→
, b→  , res→
, res→  +n, i→n]
+n, i→n]
База. 1 крок: G(dw) = |(i < b)=true |=
=ASres( S2(add, res=>, 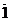 )) •ASi(S2(add, i=>,
)) •ASi(S2(add, i=>, 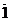 )) (dw) = ASres( S2(add,
)) (dw) = ASres( S2(add,  ,
, 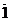 )) •ASi(S2(add,
)) •ASi(S2(add,  ,
, 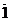 )) =ASres(
)) =ASres(  +
+ 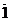 ) •ASi(
) •ASi( 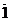 ) = dw Ñ[res→
) = dw Ñ[res→  +1, i→1] = [a→
+1, i→1] = [a→  , b→
, b→  , res→
, res→  +1, i→1]
+1, i→1]
Припущення: припустимо, що виконано t-1 кроків тіла циклу, i дані мають вид [a→  , b→
, b→  , res→
, res→  +t-1, i→t-1]. Покажемо, як зміняться дані після виконання ще одного кроку циклу:
+t-1, i→t-1]. Покажемо, як зміняться дані після виконання ще одного кроку циклу:
G([a→  , b→
, b→  , res→
, res→  +t-1, i→t-1]) = [a→
+t-1, i→t-1]) = [a→  , b→
, b→  , res→
, res→  +t, i→t]. Оскільки тіло циклу виконується, то (less, i=>, b=>) = true, тобто (i < b) = true, i < b, i = t-1, t-1 <
+t, i→t]. Оскільки тіло циклу виконується, то (less, i=>, b=>) = true, тобто (i < b) = true, i < b, i = t-1, t-1 <  i ASres(S2(add, res=>,
i ASres(S2(add, res=>, 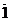 )) •ASi(S2(add, i=>,
)) •ASi(S2(add, i=>, 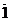 ))( [a→
))( [a→  , b→
, b→  , res→
, res→  +t-1, i→t-1]) = [a→
+t-1, i→t-1]) = [a→  , b→
, b→  , res→
, res→  +t-1, i→t-1] Ñ[ res→
+t-1, i→t-1] Ñ[ res→  +t; i→t] = [a→
+t; i→t] = [a→  , b→
, b→  , res→
, res→  +t, i→t].
+t, i→t].
Отже, гіпотезу доведено.
Таким чином, ми показали часткову коректність програми при правильних вхідних даних (тобто a>0 і b>0).
Обґрунтування повної коректності:
Покажемо, що при правильних вхідних даних програма завершується (зупиняється). Фактично, треба показати завершуваність циклу G, оскільки інші оператори не впливають на завершення програми. З часткової коректності видно, що за правильних вхідних даних перед виконанням циклу дані мають вигляд [a→  , b→
, b→  , res→
, res→  , i→0], де b > 0 і a > 0. Розглянемо послідовність значень змінної і: після кожного виконання циклу i збільшується на 1та і < b. Отже, в силу скінченності b, якщо програма входить у цикл, то він завжди завершується. При інших варіантах правильних вхідних даних програма не заходить в цикл, а послідовно виконує прості оператори, тому програма завжди зупиняється в силу скінченності кількості операторів.
, i→0], де b > 0 і a > 0. Розглянемо послідовність значень змінної і: після кожного виконання циклу i збільшується на 1та і < b. Отже, в силу скінченності b, якщо програма входить у цикл, то він завжди завершується. При інших варіантах правильних вхідних даних програма не заходить в цикл, а послідовно виконує прості оператори, тому програма завжди зупиняється в силу скінченності кількості операторів.
Завдання 1.3. За допомогою операцій віднімання і додавання одиниці розробити програму, яка обчислює результат множення цілих чисел A та B. Виконати:
1) побудувати програму для розв’язку задачі на мові SIPL,
2) побудувати композиційний семантичний терм програми,
3) довести коректність програми.
Розв’язок.
1) Програма для розв`язку задачі:
begin
R:=0;
if (N<0) then
begin
A:=-M;
B:=-N
end[S3]
else
begin
A:=M;
B:=N
end;
while (B>0)
begin
R:=R+A;
B:=B-1
end
end
begin[S4]
R:=0;
if (N<0) then
M:=-M
else
skip;
while (N<>0)
begin
R := R + M;
N := N-1
end
end
2) Семантичний композиційний терм. Для спрощення нотації ми будемо писати семантичні значення чисел-констант без знаку рисочки над власне числом (іменем константи) – розрізнити чи є число синтаксичним позначенням, чи семантичним значенням завжди можна буде по контексту.
sem_P(Program) = sem_P(Begin R:=0; if (N<0) then begin A:=-M;B:=-N end else begin A:=M;B:=N end ; while (B>0) begin R:=R+A;B:=B-1 end End)=
= sem_S( R:=0; if (N<0) ten begin A:=-M;B:=-N end else begin A:=M;B:=N end; while (B>0) begin R:=R+A;B:=B-1 end) =
= sem_S(R:= 0)•sem_S(if (N<0) then begin A:=-M;B:=-N end else begin A:=M;B:=N end; while (B>0) begin R:=R+A;B:=B-1 end) =
= ASR(sem_A(0))•sem_S(if (N<0) then begin A:=-M;B:=-N end else begin A:=M;B:=N end)•sem_S(while (B>0) begin R:=R+A;B:=B-1 end) =
= ASR(  )• IF(sem_B(N<0), sem_S( begin A:=-M;B:=-N end ), sem_S( begin A:=M;B:=N end))•WH(sem_B(B > 0), sem_S(begin R:=R+A;B:=B-1 end))=
)• IF(sem_B(N<0), sem_S( begin A:=-M;B:=-N end ), sem_S( begin A:=M;B:=N end))•WH(sem_B(B > 0), sem_S(begin R:=R+A;B:=B-1 end))=
=ASR(  )• IF(S2 (less, sem_A(N), sem_A(0)), sem_S( A:=-M;B:=-N ), sem_S( A:=M;B:=N)) •WH(S2 (gr, sem_A(B), sem_A(0)), sem_S( R:=R+A ; B:=B-1)) =
)• IF(S2 (less, sem_A(N), sem_A(0)), sem_S( A:=-M;B:=-N ), sem_S( A:=M;B:=N)) •WH(S2 (gr, sem_A(B), sem_A(0)), sem_S( R:=R+A ; B:=B-1)) =
=ASR(  )• IF(S2 (less,N=>,
)• IF(S2 (less,N=>,  ), sem_S( A:=-M) • sem_S(B:=-N), sem_S( A:=M) •sem_S ( B:=N)) •WH(S2 (gr,B=>,
), sem_S( A:=-M) • sem_S(B:=-N), sem_S( A:=M) •sem_S ( B:=N)) •WH(S2 (gr,B=>,  ), sem_S( R:=R+A) • sem_S(B:=B-1)) =
), sem_S( R:=R+A) • sem_S(B:=B-1)) =
=ASR(  )• IF(S2 (less,N=>,
)• IF(S2 (less,N=>,  ), ASA(sem_A(0-M)) • ASB(sem_A(0-N)),ASA(sem_A(M)) • ASB(sem_A(N)) •WH(S2 (gr,B=>,
), ASA(sem_A(0-M)) • ASB(sem_A(0-N)),ASA(sem_A(M)) • ASB(sem_A(N)) •WH(S2 (gr,B=>,  ), sem_S( R:=R+A) • sem_S(B:=B-1)) =
), sem_S( R:=R+A) • sem_S(B:=B-1)) =
= ASR(  )• IF(S2 (less,N=>,
)• IF(S2 (less,N=>,  ), ASA(S2 (sub, sem_A(0), sem_A(M))) • ASB(S2 (sub, sem_A(0), sem_A(N))),ASA(M=>) • ASB(N=>)) •WH(S2 (gr,B=>,
), ASA(S2 (sub, sem_A(0), sem_A(M))) • ASB(S2 (sub, sem_A(0), sem_A(N))),ASA(M=>) • ASB(N=>)) •WH(S2 (gr,B=>,  ),ASR (sem_A(R+A)) • ASB(sem_A(B-1)) =
),ASR (sem_A(R+A)) • ASB(sem_A(B-1)) =
= ASR(  )• IF(S2 (less,N=>,
)• IF(S2 (less,N=>,  ), ASA(S2 (sub,
), ASA(S2 (sub,  ,M=>)) • ASB(S2 (sub,
,M=>)) • ASB(S2 (sub,  ,N=>)),ASA(M=>) • ASB(N=>)) •WH(S2 (gr,B=>,
,N=>)),ASA(M=>) • ASB(N=>)) •WH(S2 (gr,B=>,  ),ASR (S2 (add, sem_A(R), sem_A(A))) • ASB (S2 (sub, sem_A(B), sem_A(1))))=
),ASR (S2 (add, sem_A(R), sem_A(A))) • ASB (S2 (sub, sem_A(B), sem_A(1))))=
= ASR(  )• IF(S2 (less,N=>,
)• IF(S2 (less,N=>,  ), ASA(S2 (sub,
), ASA(S2 (sub,  ,M=>)) • ASB(S2 (sub,
,M=>)) • ASB(S2 (sub,  ,N=>)),ASA(M=>) • ASB(N=>)) •WH(S2 (gr,B=>,
,N=>)),ASA(M=>) • ASB(N=>)) •WH(S2 (gr,B=>,  ),ASR (S2 (add,R=>,A=>)) • ASB (S2 (sub,B=>,
),ASR (S2 (add,R=>,A=>)) • ASB (S2 (sub,B=>,  )))
)))
3) Доведення часткової коректності.
Нехай F=ASR(  )• IF(S2 (less,N=>,
)• IF(S2 (less,N=>,  ), ASA(S2 (sub,
), ASA(S2 (sub,  ,M)) • ASB(S2 (sub,
,M)) • ASB(S2 (sub,  ,N)),ASA(M=>) • ASB(N=>)) •WH(S2 (gr,B=>,
,N)),ASA(M=>) • ASB(N=>)) •WH(S2 (gr,B=>,  ),ASR (S2 (add,R=>,A=>)) • ASB (S2 (sub,B=>,
),ASR (S2 (add,R=>,A=>)) • ASB (S2 (sub,B=>, 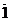 )))
)))
F1=ASR(  );
);
F2=IF(S2 (less,N=>,  ), ASA(S2 (sub,
), ASA(S2 (sub,  ,M)) • ASB(S2 (sub,
,M)) • ASB(S2 (sub,  ,N)),ASA(M=>) • ASB(N=>))
,N)),ASA(M=>) • ASB(N=>))
F3= WH(S2 (gr,B=>,  ),ASR (S2 (add,R=>,A=>)) • ASB (S2 (sub,B=>,
),ASR (S2 (add,R=>,A=>)) • ASB (S2 (sub,B=>, 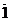 )))
)))
Тоді F= F1• F2• F3
Нехай маємо дані d=[M->m, N->n]. Доведемо, що на них програма працює правильно, тобто що при завершенні обчислень отримується бажаний результат:
F(d) = (F1• F2• F3)(d) = F3(F2(F1(d)))
F1(d)=ASR(  )(d)=ASR(
)(d)=ASR(  )([ M->m, N->n])=[ M->m, N->n] ▼[R->0]= [ M->m, N->n, R->0]= d1
)([ M->m, N->n])=[ M->m, N->n] ▼[R->0]= [ M->m, N->n, R->0]= d1
F(d)= F3(F2(F1(d)) )= F3(F2(d1)), де d1=[M->m, N->n, R->0]
F2(d1)=IF(S2 (less,N=>,  ), ASA(S2 (sub,
), ASA(S2 (sub,  ,M)) • ASB(S2 (sub,
,M)) • ASB(S2 (sub,  ,N)),ASA(M=>) • ASB(N=>))( d1)=
,N)),ASA(M=>) • ASB(N=>))( d1)=
 =
=
 =
=
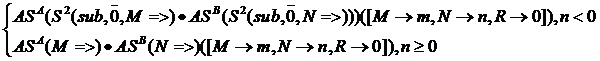 =
=
 =
=



F= F3(F2(d1)) = 
За допомогою методу математичної індукції за кількістю кроків циклу знайдемо F3(F2(d1)) , враховуючи, що n≥ 0,а потім n<0. Розглянемо спочатку випадок n≥ 0.
Гіпотеза: при виконанні n кроків тіла циклу F3(F2(d2)) = [M→m,N→n,R→m*n,A→m,B→0]
База: 0 крок: b=0 =>умова циклу не виконується ,маємо таке результуюче дане: [M→m, N→n, R→0, A→m, B→0] => R= m*n =0.Гіпотеза справджується.
Припущення: припустимо, що виконано t-1 кроків тіла циклу, тоді дані мають вигляд d*= [M→m, N→n, R→m*(t-1), A→m, B→n-t+1]. Покажемо, як зміняться дані після виконання ще одного кроку циклу :
F3 (d*)= F3 ([M→m, N→n, R→m*(t-1), A→m, B→n-t+1]) = [M→m, N→n, R→m*t, A→m, B→n-t]. Оскільки тіло циклу виконується, то S2 (gr,B=>,0) = true, тобто b>0, n-t>0 => n>t, n>n-t+1 і виконується тіло циклу ASR (S2 (add,R=>,A=>)) • ASB (S2 (sub,B=>,  )) ([M→m, N→n, R→m*(t-1), A→m, B→n-t+1]) = [M→m, N→n, R→m*(t-1), A→m, B→n-t+1] Ñ[R→ m*(t-1)+m; B→ n-t] = [M→m, N→n, R→m*t, A→m, B→n-t].При кількості кроків циклу t=n отримаємо результат [M→m N→,n, R→m*n, A→m, B→0].
)) ([M→m, N→n, R→m*(t-1), A→m, B→n-t+1]) = [M→m, N→n, R→m*(t-1), A→m, B→n-t+1] Ñ[R→ m*(t-1)+m; B→ n-t] = [M→m, N→n, R→m*t, A→m, B→n-t].При кількості кроків циклу t=n отримаємо результат [M→m N→,n, R→m*n, A→m, B→0].
Умова циклу S2 (gr,B=>,  ) = false.
) = false.
Отже, гіпотезу доведено.
Тепер аналогічно розглянемо випадок, коли n<0.
Гіпотеза: при виконанні n кроків тіла циклу F3(F2(d3)) =[ M→m, N→n, R→ (-m)*(-n), A→ -m, B→0]
База: 0 крок: b=0 => умова циклу не виконується ,маємо таке результуюче дане: [M→m, N→n, R→0, A→ -m, B→0] => R= (-m)*(-n) = 0. Гіпотеза справджується.
Припущення: припустимо, що виконано t-1 кроків тіла циклу, тоді дані мають вид d**= [M→m, N→n, R→-m*(t-1), A→ -m, B→ -n-t+1]. Покажемо, як зміняться дані після виконання ще одного кроку циклу :
F3 (d**)= F3 ([M→m, N→n, R→ (-m)*(t-1), A→ -m, B→ -n-t+1]) = [M→m, N→n, R→ (-m)*t, A→ -m, B→ -n-t]. Оскільки тіло циклу виконується, то S2 (gr,B=>,  ) = true, тобто b>0, n-t>0 => n>t, n>n-t+1 і виконується тіло циклу ASR (S2 (add,R=>,A=>)) • ASB (S2 (sub,B=>,
) = true, тобто b>0, n-t>0 => n>t, n>n-t+1 і виконується тіло циклу ASR (S2 (add,R=>,A=>)) • ASB (S2 (sub,B=>,  )) ([M→m, N→n, R→ (-m)*(t-1), A→ -m, B→ -n-t+1]) = [M→m, N→n, R→ (-m)*(t-1), A→ -m, B→ -n-t+1] Ñ[R→ (-m)*(t-1)-m; B→ -n-t] = [M→m, N→n, R→ (-m)*t, A→ -m, B→ -n-t]. При кількості кроків циклу t=-n отримаємо результат [M→m, N→n, R→ (-m)*(-n), A→ -m, B→0].
)) ([M→m, N→n, R→ (-m)*(t-1), A→ -m, B→ -n-t+1]) = [M→m, N→n, R→ (-m)*(t-1), A→ -m, B→ -n-t+1] Ñ[R→ (-m)*(t-1)-m; B→ -n-t] = [M→m, N→n, R→ (-m)*t, A→ -m, B→ -n-t]. При кількості кроків циклу t=-n отримаємо результат [M→m, N→n, R→ (-m)*(-n), A→ -m, B→0].
Умова циклу S2 (gr,B=>,  ) = false.
) = false.
Отже, гіпотезу доведено.
Обґрунтування повної коректності.
Покажемо, що при правильних вхідних даних програма завершується (зупиняється). Фактично, треба показати завершеність циклу F3 , оскільки інші оператори не впливають на завершення програми. З часткової коректності видно, що за правильних вхідних даних перед виконанням циклу дані мають вигляд [M→m, N→n, R→0, A→m, B→n]. Після кожного виконання циклу R збільшується на m і b зменшується на 1. Отже,отримаємо спадну послідовність b і в силу її скінченності, якщо програма входить у цикл, то він завжди завершується. При інших варіантах правильних вхідних даних програма не заходить в цикл, а послідовно виконує прості оператори, тому програма завжди зупиняється в силу скінченності кількості операторів.
Завдання 1.4. За допомогою операцій віднімання і додавання розробити програму, яка обчислює результат ділення rez невід’ємного числа a на додатне число b та остачу від цього ділення – ost. Виконати:
1) побудувати програму для розв’язку задачі на мові SIPL,
2) побудувати дерево синтаксичного виводу програми,
3) побудувати композиційний семантичний терм програми,
4) довести коректність програми.
Розв’язок.
1) Програма для розв’язку задачі:
Begin
rez:= 0;
k:= 0;
if (a = 0) then skip else[S5]
if (a < b) then skip else[S6]
while k <= a – b do
begin
rez:= rez+1;
k:= k+b
end;
ost:= a – k
End
2) Дерево синтаксичного виводу програми:

3) Семантичний композиційний терм:
sem_P(Program) = sem_P(Begin rez:= 0; k:= 0; if (a = 0) then skip else if (a < b) then skip else while k <= a – b do begin rez:= rez+1; k:= k+b end; ost:=a - k End)=
= sem_S(rez:= 0; k:= 0; if (a = 0) then skip else if (a < b) then skip else while k <= a – b do begin rez:= rez+1; k:= k+b end; ost:=a - k) =
= sem_S(rez:= 0)•sem_S(k:= 0; if (a = 0) then skip else if (a < b) then skip else while k <= a – b do begin rez:= rez+1; k:= k+b end; ost:=a - k)=
= sem_S(rez:= 0)•sem_S(k:= 0; if (a = 0) then skip else if (a < b) then skip else while k <= a – b do begin rez:= rez+1; k:= k+b end)•sem_S(ost:=a - k) =
= ASrez(sem_A(0))•sem_S(k:= 0)•sem_S(if (a = 0) then skip else if (a < b) then skip else while k <= a – b do begin rez:= rez+1; k:= k+b end) •ASost(sem_A(a-k))=
= ASrez(  )• ASk(sem_A(0))•IF(sem_B(a = 0), sem_S(skip), sem_S(if (a < b) then skip else while k <= a – b do begin rez:= rez+1; k:= k+b end))•ASost(S2(sub, sem_A(a), sem_A(k)))=
)• ASk(sem_A(0))•IF(sem_B(a = 0), sem_S(skip), sem_S(if (a < b) then skip else while k <= a – b do begin rez:= rez+1; k:= k+b end))•ASost(S2(sub, sem_A(a), sem_A(k)))=
= ASrez(  )• ASk(
)• ASk(  )• IF(sem_B(a = 0), sem_S(skip), sem_S(if (a < b) then skip else while k <= a – b do begin rez:= rez+1; k:= k+b end)) •ASost(S2(sub, a=>, k=>))=
)• IF(sem_B(a = 0), sem_S(skip), sem_S(if (a < b) then skip else while k <= a – b do begin rez:= rez+1; k:= k+b end)) •ASost(S2(sub, a=>, k=>))=
= ASrez(  )• ASk(
)• ASk(  )• IF(S2(eq, sem_A(a), sem_A(0)), id, IF(sem_B(a<b), sem_S(skip), sem_S(while k <= a – b do begin rez:= rez+1; k:= k+b end))) •ASost(S2(sub, a=>, k=>))=
)• IF(S2(eq, sem_A(a), sem_A(0)), id, IF(sem_B(a<b), sem_S(skip), sem_S(while k <= a – b do begin rez:= rez+1; k:= k+b end))) •ASost(S2(sub, a=>, k=>))=
= ASrez(  )• ASk(
)• ASk(  )• IF(S2(eq, a=>,
)• IF(S2(eq, a=>,  ), id, IF(S2(less, sem_A(a), sem_A(b)), id, WH(sem_B(k <= a - b), sem_S(begin rez:= rez+1; k:= k+b end)))) •ASost(S2(sub, a=>, k=>))=
), id, IF(S2(less, sem_A(a), sem_A(b)), id, WH(sem_B(k <= a - b), sem_S(begin rez:= rez+1; k:= k+b end)))) •ASost(S2(sub, a=>, k=>))=
= ASrez(  )• ASk(
)• ASk(  )• IF(S2(eq, a=>,
)• IF(S2(eq, a=>,  ), id, IF(S2(less, a=>, b=>), id, WH(S2(less, sem_A(k=>), sem_A(a-b)), sem_S(rez:= rez+1; k:= k+b)))) •ASost(S2(sub, a=>, k=>))=
), id, IF(S2(less, a=>, b=>), id, WH(S2(less, sem_A(k=>), sem_A(a-b)), sem_S(rez:= rez+1; k:= k+b)))) •ASost(S2(sub, a=>, k=>))=
= ASrez(  )• ASk(
)• ASk(  )• IF(S2(eq, a=>,
)• IF(S2(eq, a=>,  ), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), sem_S(rez:= rez+1)•sem_S(k:= k+b)))) •ASost(S2(sub, a=>, k=>))=
), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), sem_S(rez:= rez+1)•sem_S(k:= k+b)))) •ASost(S2(sub, a=>, k=>))=
= ASrez(  )• ASk(
)• ASk(  )• IF(S2(eq, a=>,
)• IF(S2(eq, a=>,  ), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez(sem_A(rez+1))•ASk(sem_A(k+b))))) •ASost(S2(sub, a=>, k=>))=
), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez(sem_A(rez+1))•ASk(sem_A(k+b))))) •ASost(S2(sub, a=>, k=>))=
= ASrez(  )• ASk(
)• ASk(  )• IF(S2(eq, a=>,
)• IF(S2(eq, a=>,  ), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, sem_A(rez), sem_A(1))))•ASk(S2(add, sem_A(k), sem_A(b)))))) •ASost(S2(sub, a=>, k=>))=
), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, sem_A(rez), sem_A(1))))•ASk(S2(add, sem_A(k), sem_A(b)))))) •ASost(S2(sub, a=>, k=>))=
= ASrez(  )• ASk(
)• ASk(  )• IF(S2(eq, a=>,
)• IF(S2(eq, a=>,  ), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, rez=>,
), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, rez=>,  )))•ASk(S2(add, k=>, b=>))))) •ASost(S2(sub, a=>, k=>))
)))•ASk(S2(add, k=>, b=>))))) •ASost(S2(sub, a=>, k=>))
4) Доведення часткової коректності:
Для скорочення запису будемо записувати дані у впорядкованому виді, тобто [a,b,rez,k,ost], замість [a→  , b→
, b→  , rez→
, rez→  , k→
, k→  , ost →
, ost →  ].
].
Позначимо
F = ASk(  )• IF(S2(eq, a=>,
)• IF(S2(eq, a=>,  ), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, rez=>,
), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, rez=>,  )))•ASk(S2(add, k=>, b=>))))) •ASost(S2(sub, a=>, k=>)),
)))•ASk(S2(add, k=>, b=>))))) •ASost(S2(sub, a=>, k=>)),
тоді маємо
sem_S([a,b,rez,k,ost])=F(ASrez(  ))([a,b,rez,k,ost])=F([a,b,rez,k,ost]Ñ[rez→0])=F([a,b,0,k,ost])
))([a,b,rez,k,ost])=F([a,b,rez,k,ost]Ñ[rez→0])=F([a,b,0,k,ost])
Позначимо
F1 = IF(S2(eq, a=>,  ), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, rez=>,
), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, rez=>,  )))•ASk(S2(add, k=>, b=>))))) •ASost(S2(sub, a=>, k=>)).
)))•ASk(S2(add, k=>, b=>))))) •ASost(S2(sub, a=>, k=>)).
Маємо
F = ASk(  )•F1
)•F1
F([a,b,0,k,ost]) =
F1(ASk(  ))([a,b,0,k,ost])=F1([a,b,0,k,ost]▼[k→0])= F1([a,b,0,0,ost]).
))([a,b,0,k,ost])=F1([a,b,0,k,ost]▼[k→0])= F1([a,b,0,0,ost]).
F1([a,b,0,0,ost]) =
IF(S2(eq, a=>,  ), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, rez=>,
), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, rez=>,  ))) •ASk(S2(add, k=>, b=>))))•ASost(S2(sub, a=>, k=>)) ([a,b,0,0,ost])=
))) •ASk(S2(add, k=>, b=>))))•ASost(S2(sub, a=>, k=>)) ([a,b,0,0,ost])=
ASost(S2(sub, a=>, k=>))(IF(S2(eq, a=>,  ), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, rez=>,
), id, IF(S2(less, a=>, b=>), id, WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, rez=>,  ))) •ASk(S2(add, k=>, b=>)))))([a,b,0,0,ost])=
))) •ASk(S2(add, k=>, b=>)))))([a,b,0,0,ost])=
 =
=  =
=
 .
.
Позначимо
G = WH(S2(less, k=>, S2(sub, a=>, b=>)), ASrez((S2(add, rez=>,  ))) •ASk(S2(add, k=>, b=>)))))
))) •ASk(S2(add, k=>, b=>)))))
Маємо F1([a,b,0,0,ost]) =

За допомогою методу математичної індукції за кількістю кроків циклу знайдемо, G([a,b,0,0,ost]), враховуючи, що a ≥ b і a ≠ 0 .
Гіпотеза: при виконанні n кроків тіла циклу G([a, b, 0, 0, ost]) = 
База. 1 крок: G([a,b,0,0,ost]) = |(k < a-b)=true => k < a-b => 0 < a-b => b<a|=
=ASrez( (S2(add, rez=>,  ))) •ASk(S2(add, k=>, b=>)))) ([a,b,0,0,ost])=ASrez( (S2(add,
))) •ASk(S2(add, k=>, b=>)))) ([a,b,0,0,ost])=ASrez( (S2(add,  ,
,  ))) •ASk(S2(add,
))) •ASk(S2(add,  , b=>))=ASrez(
, b=>))=ASrez(  ) •ASk(b=>)=[a,b,0,0,ost] Ñ[rez→1, k→b] = [a,b,1,b,ost]
) •ASk(b=>)=[a,b,0,0,ost] Ñ[rez→1, k→b] = [a,b,1,b,ost]
Припущення: припустимо, що виконано t-1 кроків тіла циклу, тоді дані мають вид [a,b,t-1,b*(t-1),ost]. Покажемо, як зміняться дані після виконання ще одного кроку циклу :
G([a,b,t-1,b*(t-1),ost]) = [a,b,t,b*t,ost]. Оскільки тіло циклу виконується, то (less, k=>, S2(sub, a=>, b=>)) = true, тобто (k < a-b) = true, k < a-b, k = t-1, t-1 < a-b виконується тіло циклу ASrez(S2(add, rez=>,  )) •ASk(S2(add, k=>, b=>))([a,b,t-1,b*(t-1),ost]) = [a,b,t-1,b*(t-1),ost] Ñ[rez→t; k→b*t] = [a,b,t,b*t,ost].
)) •ASk(S2(add, k=>, b=>))([a,b,t-1,b*(t-1),ost]) = [a,b,t-1,b*(t-1),ost] Ñ[rez→t; k→b*t] = [a,b,t,b*t,ost].
Отже, гіпотезу доведено.
Нехай G(d) зупиняється на даному : [a,b,n,b*n,ost], це значить, що умова циклу приймає значення false. Маємо : S2(less, b*n=>, (a=>)-(b=>)) = false => (b*n < a-b) = false => b*n≥a-b, враховуючи, що умова на n-1 кроі виконання циклу була істиною, маємо : b*n ≥a – b≥ b*(n-1) => b*(n+1)≥a≥b*n. Отже n – ціла частина від ділення a на b.
Маємо F1([a,b,0,0,ost]) =
=  = =
= =  =
=
=  =
=
=  =
=
= 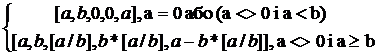
Отже, ми показали часткову коректність програми при правильних вхідних даних (тобто a≥0 і b>0).
Обґрунтування повної коректності.
Покажемо, що при правильних вхідних даних програма завершується (зупиняється). Фактично, треба показати завершеність циклу G, оскільки інші оператори не впливають на завершення програми. З часткової коректності видно, що за правильних вхідних даних перед виконанням циклу дані мають вигляд [a,b,rez=0,k=0,ost], де a ≥ b, b > 0 і a ≠ 0. Після кожного виконання циклу k збільшується на b і k+b < a. Отже, в силу скінченності a і b, якщо програма входить у цикл, то він завжди завершується. При інших варіантах правильних вхідних даних програма не заходить в цикл, а послідовно виконує прості оператори, тому програма завжди зупиняється в силу скінченності кількості операторів.
Завдання 1.5. Розробити програму, яка обчислює значення N! за вхідним цілим N з використанням одного циклу. Виконати:
1) побудувати програму для розв’язку задачі на мові SIPL,
2) побудувати дерево синтаксичного виводу програми,
3) побудувати композиційний семантичний терм програми,
4) довести коректність програми.
Розв’язок.
1) Програма для розв’язку задачі:
Begin
If N<0 then R:=0 else
begin
R:=1; M:=N;
while M>1 do begin R:=R*M; M:=M–1 end
end
End
begin[S7]
If N<0 then
R:=0
else
begin
R:=1;
while N>1 do
begin
R:=R*N;
N:=N–1
end
end
end
2) Дерево синтаксичного виводу програми:

3) Семантичний композиційний терм:
sem_P(Program) = sem_P(Begin If N<0 then R:=0 begin R:=1; M:=N; while M>1 do begin R:=R∙M; M:=M-1 end end end) = sem_S(If N<0 then R:=0 begin R:=1; M:=N; while M>1 do begin R:=R∙M; M:=M-1 end end) = IF(sem_B(N<0), sem_S(R:=0), sem_S(R:=1; M:=N while M>1 do begin R:=R∙M; M:=M-1 end) ) =IF(sem_B(N<0), sem_S(R:=0), sem_S(R:=1;M:=N) ◦ WH(sem_B(M>1), sem_S(R:=R∙M; M:=M-1) ) )= IF(sem_B(N<0), sem_S(R:=0), sem_S(R:=1) ◦ sem_S(M:=N) ◦ WH(sem_B(M>1), sem_S(R:=R∙M) ◦ sem_S( M:=M-1) ) )=
IF(S2 (less, sem_A(N), sem_A(0)), ASR(sem_A(0)), ASR(sem_A(1)) ◦ ASM(sem_A(N)) ◦ WH(S2 (gr, sem_A(M), sem_A(1)), ASR(sem_A(R∙M)) ◦ ASM(sem_A(M-1)) ) ) =IF(S2 (less, N=>,  ), ASR(
), ASR(  ), ASR(
), ASR(  ) ◦ ASM(N=>) ◦ WH(S2 (gr, M=>,
) ◦ ASM(N=>) ◦ WH(S2 (gr, M=>,  ), ASR(S2(mult, sem_A(R), sem_A(M))) ◦ ASM(S2(sub, sem_A(M), sem_A(
), ASR(S2(mult, sem_A(R), sem_A(M))) ◦ ASM(S2(sub, sem_A(M), sem_A(  ))) ) ) =IF(S2 (less, N=>,
))) ) ) =IF(S2 (less, N=>,  ), ASR(
), ASR(  ), ASR(
), ASR(  ) ◦ ASM(N=>) ◦ WH(S2 (gr, M=>,
) ◦ ASM(N=>) ◦ WH(S2 (gr, M=>,  ), ASR(S2(mult, R=>,M=>)) ◦ ASM(S2(sub, M=>,
), ASR(S2(mult, R=>,M=>)) ◦ ASM(S2(sub, M=>,  )) ) )
)) ) )
4) Доведення часткової коректності.
Нехай маємо дані d=[N->n]. Доведемо, що на них програма працює правильно, тобто що при завершенні обчислень отримується очікуваний результат:
F=IF(S2 (less, N=>,  ), ASR(
), ASR(  ), ASR(
), ASR(  ) ◦ ASM(N=>) ◦ WH(S2 (gr, M=>,
) ◦ ASM(N=>) ◦ WH(S2 (gr, M=>,  ), ASR(S2(mult, R=>,M=>)) ◦ ASM(S2(sub, M=>,
), ASR(S2(mult, R=>,M=>)) ◦ ASM(S2(sub, M=>,  )) ) )
)) ) )
F1= ASR(  );
);
F2=ASM(N=>);
F3= WH(S2 (gr, M=>,  ), ASR(S2(mult, R=>,M=>)) ◦ ASM(S2(sub, M=>,
), ASR(S2(mult, R=>,M=>)) ◦ ASM(S2(sub, M=>,  )));
)));
F4=ASR(  );
);
F5=ASR(S2(mult, R=>,M=>));
F6= ASM(S2(sub, M=>,  ));
));
1) нехай n<0
Sem_p(F)(d)= 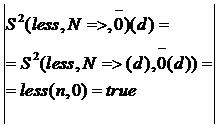 =F4(d)=F4(d▼[R->0]) =
=F4(d)=F4(d▼[R->0]) =
= F4(d▼[R->0]) = dr = [N->n, R->0] ;
факторіал для від’ємних чисел не існує і результат дорівнює нулю (помилка у ввідних даних).
2) нехай n≥0
Sem_p(F)(d)=  = F3(F2(F1(d))) =
= F3(F2(F1(d))) =
= F3(F2(d▼[R->1]) = F3(F2([N->n,R->1]) =  =
=
= F3(d1▼ [M->N=>(d1)]) = F3(d1▼ [M->n]) =  =
=
= F3(d2);
Далі за допомогою методу математичної індукції за кількістю кроків циклу знайдемо F3(d2), враховуючи, що n≥ 1, а потім n<1. Нехай спочатку n≥ 1.
Гіпотеза: при виконанні n кроків тіла циклу F3(d2)=[ 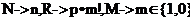 ]
]
База: Нульовий крок: При m=0 умова циклу не виконується, маємо таке результуюче дане: [  ] => R= p*m! = p. Гіпотеза справджується.
] => R= p*m! = p. Гіпотеза справджується.
Припущення: припустимо, що виконано t-1 кроків тіла циклу, тоді дані мають вид dw= [N->n,R->p,M->t-1]. Покажемо, як зміняться дані після виконання ще одного кроку циклу:
F3 (dw)= F3 ([N->n,R->p,M->t]) =  ;
;
При t=0:
F3 (dw) = F3 ([N->n,R->p,M->0])= [N->n,R->p,M->0];
dr = [N->n,R->p∙0!,M->0] = dw; гіпотеза справджується.
При t>0:
F3 (dw) = F5 ◦ F6 ◦ F3(dw) =  = F3(dd) =
= F3(dd) =
=  =
=  = dq = dr;
= dq = dr;
 => F3(dw) =
=> F3(dw) = 
Отже, гіпотезу доведено.
Обчислення завершене. Результат поміщується у вихідному даному R. Маємо R->1∙n!. Оскільки у вхідному даному значення змінної N було n, то дійсно отримали обчислення факторіалу.
Обґрунтування повної коректності.
Покажемо, що при правильних вхідних даних програма завершується (зупиняється). Фактично, треба показати завершуваність циклу F3 , оскільки інші оператори не впливають на завершення програми. З часткової коректності видно, що за правильних вхідних даних перед виконанням циклу дані мають вигляд [N->n,R->1,M->m] (де n>0). Після кожного виконання циклу R збільшується у m разіві m зменшується на 1. Отже,отримаємо спадну послідовність m і в силу її скінченності, якщо програма входить у цикл, то він завжди завершується. При інших варіантах правильних вхідних даних програма не заходить в цикл, а послідовно виконує прості оператори, тому програма завжди зупиняється в силу скінченності кількості операторів.
Завдання 1.6. Розробити програму, яка за допомогою операції додавання обчислює результат піднесення значення a до степеня b. Оба числа додатні. Виконати:
1) побудувати програму для розв’язання задачі на мові SIPL,
2) побудувати дерево синтаксичного виводу програми,
3) побудувати композиційний семантичний терм програми,
4) довести коректність програми.
Розв’язок.
1) Програма на мові SIPL, яка обчислює a^b через додавання
begin
i:=1;
r:=1;
while i ≤ b do
begin
k:=1;
p:=r;
while a ≠ k do
begin
r:=r+p;
k:=k+1
end;
i:=i+1
end
end
begin[S8]
r:=1;
while b>0 do
begin
k:=1;
p:=r;
while k<a do
begin
r:=r+p;
k:=k+1
end;
b:=b-1
end
end
2)  Дерево синтаксичного виводу програми :
Дерево синтаксичного виводу програми :
3) Семантичний терм програми:
Sem_P(a^b) = Sem_P(begin i:=1;r:=1;while i≤b do begin k:=1;p:=r; while a≠ k do begin r:=r+p; k:=k+1 end; i:=i+1 end end) =
Sem_S(i:=1;r:=1;while i≤b do begin k:=1;p:=r; while a≠ k do begin r:=r+p; k:=k+1 end; i:=i+1 end) =
Sem_S(i:=1) ◦ Sem_S(r:=1) ◦ Sem_S(while i≤b do begin k:=1;p:=r; while a≠ k do begin r:=r+p; k:=k+1 end; i:=i+1 end) =
ASi(Sem_A(1)) ◦ ASr(Sem_A(1)) ◦ WH(Sem_B(i≤b),Sem_S(begin k:=1;p:=r; while a≠ k do begin r:=r+p; k:=k+1 end; i:=i+1 end))=
ASi(  ) ◦ ASr(
) ◦ ASr(  ) ◦WH(S2(leq,Sem_A(i),Sem_A(b)),Sem_S(k:=1;p:=r; while a≠ k do begin r:=
) ◦WH(S2(leq,Sem_A(i),Sem_A(b)),Sem_S(k:=1;p:=r; while a≠ k do begin r:=
r+p; k:=k+1 end; i:=i+1)) =
ASi(  ) ◦ ASr(
) ◦ ASr(  ) ◦WH(S2(leq,i=>,b=>),Sem_S(k:=1) ◦Sem_S(p:=r) ◦ Sem_S(while a≠ k do begin r:=r+p; k:=k+1 end; i:=i+1)) =
) ◦WH(S2(leq,i=>,b=>),Sem_S(k:=1) ◦Sem_S(p:=r) ◦ Sem_S(while a≠ k do begin r:=r+p; k:=k+1 end; i:=i+1)) =
ASi(  ) ◦ ASr(
) ◦ ASr(  ) ◦WH(S2(leq,i=>,b=>),ASk(Sem_A(1)) ◦ASp(Sem_A(r)) ◦ WH(Sem_B (a≠ k) , Sem_S(begin r:=r+p; k:=k+1 end)) ◦Sem_S( i:=i+1) =
) ◦WH(S2(leq,i=>,b=>),ASk(Sem_A(1)) ◦ASp(Sem_A(r)) ◦ WH(Sem_B (a≠ k) , Sem_S(begin r:=r+p; k:=k+1 end)) ◦Sem_S( i:=i+1) =
ASi(  ) ◦ ASr(
) ◦ ASr(  ) ◦WH(S2(leq,i=>,b=>),ASk(
) ◦WH(S2(leq,i=>,b=>),ASk(  ) ◦ASp(r=>) ◦ WH(S2(neq,Sem_A (a),Sem_A (k)) , Sem_S(r:=r+p; k:=k+1)) ◦ASi(Sem_A(i+1)) =
) ◦ASp(r=>) ◦ WH(S2(neq,Sem_A (a),Sem_A (k)) , Sem_S(r:=r+p; k:=k+1)) ◦ASi(Sem_A(i+1)) =
ASi(  ) ◦ ASr(
) ◦ ASr(  ) ◦WH(S2(leq,i=>,b=>),ASk(
) ◦WH(S2(leq,i=>,b=>),ASk(  ) ◦ASp(r=>) ◦ WH(S2(neq,a=>,k=>) , Sem_S(r:=r+p) ◦Sem_S(k:=k+1)) ◦ASi(S2 (add,Sem_A(i),Sem_A(1))) =
) ◦ASp(r=>) ◦ WH(S2(neq,a=>,k=>) , Sem_S(r:=r+p) ◦Sem_S(k:=k+1)) ◦ASi(S2 (add,Sem_A(i),Sem_A(1))) =
ASi(  ) ◦ ASr(
) ◦ ASr(  ) ◦WH(S2(leq,i=>,b=>),ASk(
) ◦WH(S2(leq,i=>,b=>),ASk(  ) ◦ASp(r=>) ◦ WH(S2(neq,a=>,k=>) , ASr(Sem_A(r+p)) ◦ASk (Sem_A(k+1))) ◦ASi(S2 (add,i=>,
) ◦ASp(r=>) ◦ WH(S2(neq,a=>,k=>) , ASr(Sem_A(r+p)) ◦ASk (Sem_A(k+1))) ◦ASi(S2 (add,i=>,  )) =
)) =
ASi(  ) ◦ ASr(
) ◦ ASr(  ) ◦WH(S2(leq,i=>,b=>),ASk(
) ◦WH(S2(leq,i=>,b=>),ASk(  ) ◦ASp(r=>) ◦ WH(S2(neq,a=>,k=>) , ASr(S2(add,Sem_A(r),Sem_A(p))) ◦ASk (S2(add,Sem_A(k),Sem_A(1))) ) ◦ASi(S2 (add,i=>,
) ◦ASp(r=>) ◦ WH(S2(neq,a=>,k=>) , ASr(S2(add,Sem_A(r),Sem_A(p))) ◦ASk (S2(add,Sem_A(k),Sem_A(1))) ) ◦ASi(S2 (add,i=>,  )) =
)) =
ASi(  ) ◦ ASr(
) ◦ ASr(  ) ◦WH(S2(leq,i=>,b=>),ASk(
) ◦WH(S2(leq,i=>,b=>),ASk(  ) ◦ASp(r=>) ◦ WH(S2(neq,a=>,k=>) , ASr(S2(add,r=>,p=>)) ◦ASk (S2(add,k=>,
) ◦ASp(r=>) ◦ WH(S2(neq,a=>,k=>) , ASr(S2(add,r=>,p=>)) ◦ASk (S2(add,k=>,  )) ) ◦ASi(S2 (add,i=>,
)) ) ◦ASi(S2 (add,i=>,  )) )
)) )
4) Довести коректність програми
а) Часткова коректність
Нехай st = [a®m, b®n], m>0, n≥0. Тоді необхідно показати, що якщо Sem_P(a^b)(st)↓ = str, то rÞ(str) = m^n.
Для зручності позначимо: p1 = S2(neq,aÞ,kÞ) ,
f1 = ASr(S2(add,rÞ,pÞ)) ◦ASk(S2(add,kÞ,  )) , mul(a, r) = WH(p1, f1) ,
)) , mul(a, r) = WH(p1, f1) ,
p2 = S2(leq, iÞ,bÞ) , f2= ASk(  ) ◦ASp(rÞ) ◦ mul(a, r) ◦ASi(S2 (add,iÞ,
) ◦ASp(rÞ) ◦ mul(a, r) ◦ASi(S2 (add,iÞ,  ))
))
Тоді програму можна записати у вигляді:
Sem_P(a^b) = ASi(  ) ◦ ASr(
) ◦ ASr(  ) ◦WH(p2,f2)
) ◦WH(p2,f2)
Спочатку покажемо, що mul(a, r) ([a®a0, k®k0, r®r0, p®p0]) = [a®a0, k®a0, r®r0+(a0–k0)*p0, p®p0] , для a0–k0 ≥ 0. Доведемо це індукцією за величиною t = (a0–k0) = (aÞ –kÞ). Позначимо st0 = [a®a0, k®k0, r®r0, p®p0].
База індукції: t = 0. У цьому випадку st0 = [a®a0, k®a0, r®r0, p®p0]. Перевіримо: mul(a, r) (st0) = WH(p1, f1) (st0) = WH(S2(neq,aÞ,kÞ), f1) (st0) = | neq(aÞ,kÞ) (st0) = neq(a0, a0) = false | = st0 = [a®a0, k®a0, r®r0+(a0–k0)*p0, p®p0]. Отже, базу індукції доведено.
Крок індукції: припустимо, що для всіх t £ H (H ≥ 0) виконується припущення індукції mul(a, r) ([a®a0, k®k0, r®r0, p®p0]) = [a®a0, k®a0, r®r0+(a0–k0)*p0, p®p0] , для a0–k0≥0 і покажемо, що при t = H+  припущення також вірне. Обчислимо mul(a, r) (st0), де a0–k0 = H+
припущення також вірне. Обчислимо mul(a, r) (st0), де a0–k0 = H+  (H ≥ 0): mul(a, r) (st0) = WH(S2(neq,aÞ,kÞ), f1) (st0) = | neq(aÞ,kÞ) (st0) = neq(a0, a0– (H+
(H ≥ 0): mul(a, r) (st0) = WH(S2(neq,aÞ,kÞ), f1) (st0) = | neq(aÞ,kÞ) (st0) = neq(a0, a0– (H+  )) = false | = ( f1 ◦ mul(a, r) ) (st0) = mul(a, r) (f1(st0)) = mul(a, r) ( (ASr(S2(add,rÞ,pÞ)) ◦ASk(S2(add,kÞ,
)) = false | = ( f1 ◦ mul(a, r) ) (st0) = mul(a, r) (f1(st0)) = mul(a, r) ( (ASr(S2(add,rÞ,pÞ)) ◦ASk(S2(add,kÞ,  )) ) (st0) ) = mul(a, r) ([a®a0, k® k0+
)) ) (st0) ) = mul(a, r) ([a®a0, k® k0+  , r®r0+p0, p®p0]) = | тепер (aÞ –kÞ) = a0 –(k0+
, r®r0+p0, p®p0]) = | тепер (aÞ –kÞ) = a0 –(k0+  ) = a0 –(a0– H) =H, отже можна застосувати припущення індукції для t = H | = [a®a0, k®a0, r®(r0+p0)+(a0–(k0+
) = a0 –(a0– H) =H, отже можна застосувати припущення індукції для t = H | = [a®a0, k®a0, r®(r0+p0)+(a0–(k0+  ))*p0, p®p0] = [a®a0, k®a0, r®r0+(a0–k0)*p0, p®p0]. Отже, для t = H+
))*p0, p®p0] = [a®a0, k®a0, r®r0+(a0–k0)*p0, p®p0]. Отже, для t = H+  припущення також вірне.
припущення також вірне.
Тепер покажемо, що WH(p2,f2) ([a®a0, b®b0, r®r0, i®i0]) = [a®a0, b®b0, r®r0*a0^(b0–i0+  ), i®b0+
), i®b0+  , k®kx, p®px] для b0–i0+
, k®kx, p®px] для b0–i0+  ≥0. Доведемо це твердження індукцією за величиною t = (b0–i0+
≥0. Доведемо це твердження індукцією за величиною t = (b0–i0+  ) = (bÞ –iÞ +
) = (bÞ –iÞ +  ). Позначимо st0 = [a®a0, b®b0, r®r0, i®i0].
). Позначимо st0 = [a®a0, b®b0, r®r0, i®i0].
База індукції: t = 0. У цьому випадку st0 = [a®a0, b®b0, r®r0, i®b0+  ]. Перевіримо: WH(p2,f2) (st0) = WH(S2(leq, iÞ,bÞ), f2) (st0) = | leq(iÞ,bÞ) (st0) = leq(b0+
]. Перевіримо: WH(p2,f2) (st0) = WH(S2(leq, iÞ,bÞ), f2) (st0) = | leq(iÞ,bÞ) (st0) = leq(b0+  , b0) = false | = st0 = [a®a0, b®b0, r®r0*a0^(0), i®b0+
, b0) = false | = st0 = [a®a0, b®b0, r®r0*a0^(0), i®b0+  ] = [a®a0, b®b0, r®r0*a0^(b0–i0+
] = [a®a0, b®b0, r®r0*a0^(b0–i0+  ), i®b0+
), i®b0+  ] . Отже, базу індукції доведено.
] . Отже, базу індукції доведено.
Крок індукції: припустимо, що для всіх t £ H (H ≥ 0) виконується припущення індукції WH(p2,f2) ([a®a0, b®b0, r®r0, i®i0]) = [a®a0, b®b0, r®r0*a0^(b0–i0+  ), i®b0+
), i®b0+  , k®kx, p®px] , для 0 £ b0–i0+
, k®kx, p®px] , для 0 £ b0–i0+  £ H (тобто 0 £ bÞ –iÞ +
£ H (тобто 0 £ bÞ –iÞ +  £ H) і покажемо, що при t = H+
£ H) і покажемо, що при t = H+  припущення також вірне. Обчислимо WH(p2,f2) (st0), де b0–i0+
припущення також вірне. Обчислимо WH(p2,f2) (st0), де b0–i0+  = H+
= H+  (H ≥ 0) у стані st0: WH(p2,f2) (st0) = WH(S2(leq, iÞ,bÞ),f2) (st0) = | leq(iÞ,bÞ) (st0) = leq(i0, b0) = true, оскільки i0 = b0 – H у st0 | = ( f2 ◦ WH(p2,f2) ) (st0) = WH(p2,f2) (f2(st0)) = WH(p2,f2) (ASk(
(H ≥ 0) у стані st0: WH(p2,f2) (st0) = WH(S2(leq, iÞ,bÞ),f2) (st0) = | leq(iÞ,bÞ) (st0) = leq(i0, b0) = true, оскільки i0 = b0 – H у st0 | = ( f2 ◦ WH(p2,f2) ) (st0) = WH(p2,f2) (f2(st0)) = WH(p2,f2) (ASk(  ) ◦ASp(rÞ) ◦ mul(a, r) ◦ASi(S2(add,iÞ,
) ◦ASp(rÞ) ◦ mul(a, r) ◦ASi(S2(add,iÞ,  )) (st0)) = WH(p2,f2) (ASi(S2(add,iÞ,
)) (st0)) = WH(p2,f2) (ASi(S2(add,iÞ,  )) ( mul(a, r) ( [a®a0, b®b0, r®r0, i®i0, k®
)) ( mul(a, r) ( [a®a0, b®b0, r®r0, i®i0, k®  , p®r0] ) ) ) = WH(p2,f2) ( ASi(S2(add,iÞ,
, p®r0] ) ) ) = WH(p2,f2) ( ASi(S2(add,iÞ,  )) ([a®a0, b®b0, r®r0+(a0–
)) ([a®a0, b®b0, r®r0+(a0–  )*r0, i®i0, k®a0, p®r0]) ) = WH(p2,f2) ([a®a0, b®b0, r®a0*r0, i®i0+
)*r0, i®i0, k®a0, p®r0]) ) = WH(p2,f2) ([a®a0, b®b0, r®a0*r0, i®i0+  , k®a0, p®r0]) = | тепер t = bÞ –iÞ +
, k®a0, p®r0]) = | тепер t = bÞ –iÞ +  = b0–( i0+
= b0–( i0+  )+
)+  = H, отже можна скористатися припущенням індукції та отримати наступне | = [a®a0, b®b0, r®a0*r0*a0^(b0–(i0+
= H, отже можна скористатися припущенням індукції та отримати наступне | = [a®a0, b®b0, r®a0*r0*a0^(b0–(i0+  )+
)+  ), i®b0+
), i®b0+  , k®kx, p®px] = [a®a0, b®b0, r®r0*a0^(b0–i0+
, k®kx, p®px] = [a®a0, b®b0, r®r0*a0^(b0–i0+  ), i®b0+
), i®b0+  , k®kx, p®px], що і потрібно було довести. Отже, для t = H+
, k®kx, p®px], що і потрібно було довести. Отже, для t = H+  припущення також вірне.
припущення також вірне.
Тепер, Sem_P(a^b) (st) = ASi(  ) ◦ ASr(
) ◦ ASr(  ) ◦WH(p2,f2) (st) = WH(p2,f2) ( ASr(
) ◦WH(p2,f2) (st) = WH(p2,f2) ( ASr(  ) ( ASi(
) ( ASi(  ) ( [a®m, b®n] ) ) ) = WH(p2,f2) ( [a®m, b®n, i®
) ( [a®m, b®n] ) ) ) = WH(p2,f2) ( [a®m, b®n, i®  , r®
, r®  ] ) = [a®m, b®n, r®
] ) = [a®m, b®n, r®  *m^(n–
*m^(n–  +
+  ), i®n+
), i®n+  , k®kx, p®px] = [a®m, b®n, r®m^n, i®n+
, k®kx, p®px] = [a®m, b®n, r®m^n, i®n+  , k®kx, p®px] = str, тобто rÞ(str) = m^n. Ми отримали очікуваний результат обчислень за програмою.
, k®kx, p®px] = str, тобто rÞ(str) = m^n. Ми отримали очікуваний результат обчислень за програмою.
Отже, твердження доведене і програма є частково коректною.
б) Тотальна коректність
Покажемо, що обчислення за програмою завжди зупиняються.
Для початку доведемо завершуваність циклу WH(p1, f1). Позначимо st0=st (початковий стан для циклу WH(p1, f1)), st1=f1(st0), st2=f1(st1) і т.д. Для того, щоб цикл завершувався, потрібно показати, що існує такий стан, на якому виконується умова aÞ =kÞ або aÞ –kÞ = 0. Припустимо, що такого стану не існує. Тоді розглянемо послідовність різниць цих змінних, яка має бути нескінченою:
t0= aÞ(st0) –kÞ(st0), t1= aÞ(st1) –kÞ(st1), t2= aÞ(st2) –kÞ(st2), …
Очевидно, що t0 ≥ 0 в початковому стані st0, і те, що t0 > t1 > t2… , тобто послідовність є строго спадною. Тоді ця послідовність не є нескінченою, оскільки вона обмежена знизу числом 0 (різницею однакових чисел), що і треба було довести.
Аналогічно покажемо завершуваність циклу WH(p2, f2). Позначимо st0=st (початковий стан для циклу WH(p2, f2)), st1=f2(st0), st2=f2(st1) і т.д. Для того, щоб цикл завершувався, потрібно показати, що існує такий стан, на якому виконується умова iÞ > bÞ або bÞ –iÞ < 0. Припустимо, що такого стану не існує. Тоді розглянемо послідовність різниць таких змінних, яка має бути нескінченою:
t0= bÞ(st0) –iÞ(st0), t1= bÞ(st1) –iÞ(st1), t2= bÞ(st2) –iÞ(st2), …
Відомо, що b не змінює своє значення протягом виконання циклу і є фіксованим невід’ємним значенням. Оскільки змінна i на кожній ітерації збільшує своє значення на 1, то можна стверджувати, що t0 > t1 > t2… , тобто послідовність є строго спадною. Тоді ця послідовність не є нескінченою, оскільки вона обмежена знизу числом 0, отже, змінна i набуде значення змінної b – що і потрібно було показати.
Таким чином, з часткової коректності та факту зупинки циклів (внутрішнього та зовнішнього) випливає тотальна коректність програми, що розглядається.
Дата добавления: 2018-04-05; просмотров: 663; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
