Жизнь – это не просто годы, посвященные ублажению самих себя и собственной карьере. Это привилегия, ответственность, необходимость жить, следуя за высшим призванием. © Элизабет Доул 1356 - | 816 - или читать все...
Обратная связь Пожаловаться на материал

Образец выполнения лабораторной работы

Индивидуальная работа №2

Тема: Оценки параметров распределения. Гистограмма частот.

Цель:1. Нахождение оценок параметров распределения.

       2. Построение гистограммы частот.

 

Указание: Работу провести с использования таблиц Exсel.

Задание 1.

Серия А.

При оценке свойств сахарной свеклы было обследовано n проб и получены следующие значения содержания сахара X %.

Требуется:

1) определить выборочную среднюю Хв, выборочную и исправленную дисперсии.

2) полагая, что распределение признака X описывается законом нормального распределения, найдите доверительный интервал для среднего содержания сахара в обследуемой партии свеклы на уровне заданной надежности γ.

 Исходная информация в таблице №1.

Таблица №1

№ вар.   1   2   3   4   5   6   7   8   9   10  
    15,5   12,4   12,3   14,8   11,6   15,4   15,1   16,1   14,1   14,2  
    16,0   14,1   11,0   11,5   14,5   15,8   15,5   17,1   15,1   13,6  
    14,6   13,2   11,8   12,1   13,8   15,1   143   17,2   12,2   15,2  
Значения   14,9   14,0   13,2   13,4   12,0   14,9   16,6   16,9   13,8   13,0  
    15,3   14,1   14,0   13,1   13,8   14,5   16,2   15,2   14,1   15,9       
Xi   14,0   14,0   14,1   11,9   14,2   13,5   16,1   14,3   15,9   15,2  
    14,3   14,6   12,0   12,8   13,4   13,0   15,4   15,5   16,8   16,5  
    15,1   14,0   13,6   13,5   14,2   13,2   14,9   16,2   12,5   13,9  
    15,4   13,4   11,3   14,2   14,5   13,3   15,5   14,1   13,4   14,2  
    16,0   12,2       12,9   11,0   14,0       15,0   16,0   15,3  
    15,7   12,3               14,1               16,4  
                                        15,0  
n   11 11 9   10   10   11   9   10   10   12  
γ   0,95   0,99   0,999   0,95   0,99   0,999   0,95   0,99   0,999   0,99  

 

Серия Б.

 

При изучении физико-механических свойств обувных кож было испытано n образцов и получены следующие значения предела прочности на разрыв Z н/мм2.

Требуется:

1) определить выборочную среднюю Zв, выборочную и исправленную дисперсии;

2) полагая, что распределение величины Z описывается нормальным законом найдите доверительный интервал для среднего предела прочности этой кожи на уровне надежности γ.

 Исходная информация в таблице №2.

Таблица №2

 

№вар.   1   2   3   4   5   6   7   8   9   10  
    22,4   15,5   26,9   24,8   24,3   20,0   24,7   19,5   18,0   21,1  
    18,3   19,2   26,3   20,1   22,8   19,1   25,2   21,8   20,3   23,4  
    16,4   15,7   27,2   22,4   18,0   18,8   21,7   22,3   16,1   23,8  
Значения 20,6   16,2   25,5   27,2   19,4   17,9   24,3   18,4   18,9   26,3  
  19,5   17,5   26,6   26,4   23,3   16,2   23,8   22,9   21,5   25,5  
Zi   21,7   18,2   26,7   25,6   20,2   19,1   24,5   19,3   22,3   25,5  
    18,8   17,1   25,8   21,1    17,1   22,5   22,4   23,1   19,3   21,0  
    20,1   19,4   27,1   24,6   17,5   21,3   23,9   22,6   16,0   25,1  
    17,1   16,8   26,0   26,8   18,8   20,3   23,1   21,2   17,7   23,0  
    19,3   20,0   25,1   25,2   23,7   17,0   26,1   22,7   19,0   26,1  
        19,5   26,5   22,9       16,1       20,0   19,1   25,4  
        14,6               19,9           20,0      
n   10   12   11   11   10   12   10   11   12   11  
γ   0,999   0,95   0,99   0,95   0,95   0,999   0,99   0,999   0,99   0,95  

 

Серия В

 

При оценке перспективности месторождения был произведен анализ n проб руды и получены следующие значения содержания окиси железа X %.

 Требуется:

1) Определить выборочную среднюю Хв, выборочную и исправленную дисперсии;

2) считая, что распределение величины X описывается нормальным законом, найдите доверительный интервал для среднего содержания окиси железа в обследуемой руде на уровне надежности γ.

Исходная информация в таблице №3.

Таблица №3

№ вар. 1   2   3   4   5   6   7   8   9   10  
    34,6   35,1   39,2   41,0   38,7   43,2   40,1   36,2   44,5   39,5  
    40,5 34,0   37,1   42,0   39,1   42,5   39,4   37,9   46,7   42,4  
    39,1   32,7   34,5   39,8   40,0   43,4   43,3   39,1   44,8   38,3  
Значе-   33,5   33,3   38,0   41,7   39,2   44,1   44,3   42,5   46,3   41,7  
ния   40,2   34,7   37,9   43,1   41,3   42,9   37,1   41,3   42,4   40,1  
    36,7   36,0   35,5   40,6   35,5   43,5   43,7   40,3   40,1   39,3  
Xi   36,2   35,8   34,8   38,7   37,9   40,1   38,8   37,0   47,1   36,4  
    39,3   34,3   33,0   42,3   36,2   43,8   37,5   36,1   45,5   37,1  
    36,5   32,7   36,3   43,9   39,3   42,0   38,0   39,9   45,1   38,8  
    39,2   35,0   40,1   40,5   42,3   44,3   42,8   40,0   41,0   40,6  
    37,1       32,5   37,1   41,5   45,1       39,1   42,8      
    40.4               38.9           38.7          
n   12   10   11   11   12   11   10   12   11   10  
γ   0,999   0,99   0,95   0.999   0.999   0,95   0,95   0.99   0.99   0,95  

Задание 2.

Серия А

 

С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определённых половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х (табл. 5). Требуется:

1. Построить гистограмму относительных частот для наблюдаемых значений признака Х.

2. Определить выборочную среднюю, выборочную и исправленные дисперсии.

3. Используя полученные результаты и полагая, что распределение признака Х подчинено нормальному закону, найдите:

a) доверительный интервал для ожидаемого среднего значения обхвата груди на уровне надёжности γ;

b) вероятность того, что величина признака Х , у выбранного наугад из данной группы ребёнка окажется в пределах от α до β см (табл. 6)

Таблица 5

Обхват груди

Х, см

Количество детей для вар№
1 2 3 4 5 6 7 8 9 10
56-58 13       28       35 5
59-61 28   27   48 16 33   52 18
62-64 40 11 40 42 70 47 54 21 71 57
65-67 47 37 44 51 78 64 66 36 67 49
68-70 41 64 48 67 36 54 55 78 44 30
71-73 21 74 34 74 20 37 30 69 31 21
74-76   30 17 54   22 12 49    
77-79   14   32       27    
Итого 190 230 210 320 280 240 250 280 300 180

Таблица 6

Номер варианта 1 2 3 4 5 6 7 8 9 10
γ 0,95 0,999 0,95 0,99 0,95 0,99 0,999 0,999 0,99 0,95
α, см 66 62 72 69 58 64 63 67 60 65
β, см 70 66 78 77 66 68 69 72 65 71

Серия Б

 

С целью определения рациональной структуры размерного ассортимента детской обуви проведено выборочное обследование определённых половозрастных групп детского населения и получено следующее распределение количества детей по величине длины стопы Z (табл. 7). Требуется:

1. Построить гистограмму относительных частот для наблюдаемых значений признака Z.

2. Определить выборочную среднюю, выборочную и исправленные дисперсии.

3. Используя полученные результаты и полагая, что распределение признака Z подчинено нормальному закону, найдите:

а) доверительный интервал для ожидаемого среднего значения обхвата груди на уровне надёжности γ;

б) вероятность того, что величина признака Z , у выбранного наугад из данной группы ребёнка окажется в пределах от α до β см (табл. 8)

Таблица 7

Длина стопы

Z ,мм

Количество детей для вар№
1 2 3 4 5 6 7 8 9 10
171-175 17     24     14 12    
176-180 46 13 22 46   43 27 38    
181-185 65 28 29 53 36 50 45 67 17 22
186-190 53 57 50 42 51 66 42 77 34 35
191-195 38 66 56 33 72 74 39 31 46 78
196-200 21 55 18 22 66 55 23 15 40 69
201-205   41 5   45 32     37 49
206-210         30       26 27
Итого 240 260 180 220 300 320 190 140 200 280

 

Таблица 8

Номер варианта 1 2 3 4 5 6 7 8 9 10
γ 0,999 0,95 0,99 0,95 0,999 0,999 0,99 0,95 0,99 0,99
α , см 179 189 185 177 191 184 187 183 192 190
β , см 187 196 194 186 198 197 193 195 203 201

 

Серия В

 

С целью определения рациональной структуры размерного ассортимента детской одежды проведено выборочное обследование определённых половозрастных групп детского населения и получено следующее распределение количества детей по величине обхвата груди Х (табл. 9). Требуется:

1. Построить гистограмму относительных частот для наблюдаемых значений признака Х.

2. Определить выборочную среднюю, выборочную и исправленные дисперсии.

3. Используя полученные результаты и полагая, что распределение признака Х подчинено нормальному закону, найдите:

а) доверительный интервал для ожидаемого среднего значения обхвата груди на уровне надёжности γ;

б) вероятность того, что величина признака Х , у выбранного наугад из данной группы ребёнка окажется в пределах от α до β см (табл. 10)

Таблица 9

Обхват груди

Х, см

Количество детей для вар№
1 2 3 4 5 6 7 8 9 10
56-58 14       29       36 6
59-61 29   28   49 17 34   53 19
62-64 41 12 41 43 71 48 55 22 72 58
65-67 48 38 45 52 79 65 67 37 68 50
68-70 42 65 49 68 37 55 56 79 45 31
71-73 22 75 35 75 21 38 31 70 32 22
74-76   31 18 55   23 13 50    
77-79   15   33       28    
Итого 196 236 216 326 286 246 256 286 306 186

 

Таблица 10

Номер варианта 1 2 3 4 5 6 7 8 9 10
γ 0,95 0,999 0,95 0,99 0,95 0,99 0,999 0,999 0,99 0,95
α , см 66 62 72 69 58 64 63 67 60 65
β , см 70 66 78 77 66 68 69 72 65 71

 


Образец выполнения лабораторной работы.

Задание 1.

При оценке свойств винограда было обследовано 10 проб и получены следующие значения содержания углеводов Y (г/100 г): 17,1; 16,2; 18,3; 16,6; 15,3; 18,6; 16,4; 16,5; 17,5; 16,9. Требуется: 1) определить выборочную среднюю 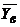, выборочную Dв и исправленную S2 дисперсии; 2) полагая, что распределение признака Y описывается нормальным законом распределения, найдите доверительный интервал для среднего содержания а углеводов в обследуемой партии винограда на уровне заданной надежности  g = 0,999.

Решение.

1) Определим выборочную среднюю 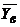, выборочную Dв и исправленную S2 дисперсии. Вспомогательные расчеты проведем в таблице.

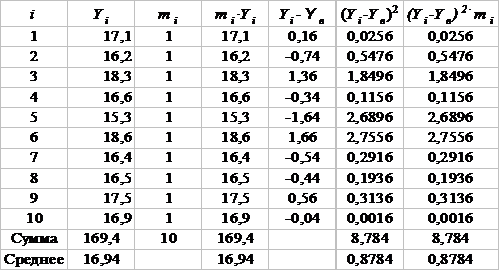
Выборочная средняя .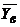

Выборочная дисперсия Dв .

Исправленная дисперсия s2 .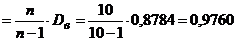

2) Полагая, что распределение признака Y описывается нормальным законом распределения, найдём доверительный интервал для среднего содержания а углеводов в обследуемой партии винограда на уровне заданной надежности  g = 0,999. Доверительный интервал найдём по формуле:

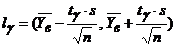, где . по таблице (см. приложение 3 в [ 8 ]) по заданным n=10  g = 0,999 находим tg=4,78.

Итак, 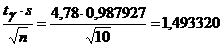 и доверительный интервал

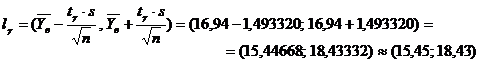
Ответ: Выборочная средняя 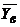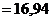; выборочная дисперсия Dв ; исправленная дисперсия s2 .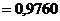

С надёжностью 0,999 среднее содержание а углеводов в обследуемой партии винограда заключено в доверительном интервале 15,45 < а < 18,43.

 

Задание 2.

С целью определения месячного дохода работников банка, была обследована группа специалистов и получено следующее распределение количества работников по величине заработной платы X (у.е.). Требуется: 1) построить гистограмму относительных частот для наблюдаемых значений признака X; 2) определить выборочную среднюю, выборочную и исправленную дисперсии; 3) используя полученные результаты и полагая, что распределение признака X подчинено нормальному закону, найдите: а) доверительный интервал для ожидаемого среднего значения заработной платы на уровне надежности  g = 0,99; б) вероятность того, что величина признака X у выбранного наугад из данной группы работника окажется в пределах от 196 у.е. до 202 у.е. Исходная информация:

Зар. плата

X, у.е.

 Количество работников

187-189

 1

190-192

 4

193-195

 7

196-198

 8

199-201

 25

202-204

 29

205-207

 19

208-210

 8

Итого

 101

 

Решение.

1. построим гистограмму относительных частот для наблюдаемых значений признака X. Для этого перейдём к частичным интервалам, разбив весь промежуток (187,210) на 8 промежутков равной длины . Для каждого из них найдём значения плотности относительных частот 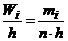 (i =1,2,…,n). Расчеты проводим в следующей таблице:

Построим гистограмму относительных частот:

2. определим выборочную среднюю, выборочную и исправленную дисперсии. Для упрощения расчетов перейдём к условным вариантам , где xi – середина i-го интервала, C = 203 – ложный нуль (варианта с наибольшей частотой), h = 3 – шаг, т.е. разность между любыми двумя соседними первоначальными вариантами. Расчеты проводим в следующей таблице:

Проверим правильность выполненных расчетов:

.

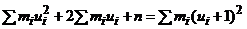260+2∙(-48)+101=265;

265=265. Вычисления произведены правильно.

Вычислим условные моменты первого и второго порядков:

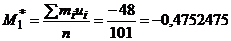
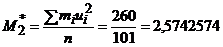
Вычислим выборочную среднюю и выборочную дисперсию:

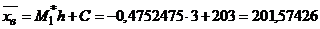
Исправленная дисперсия s2 .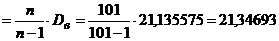

3. используя полученные результаты и полагая, что распределение признака X подчинено нормальному закону, найдём:

а) доверительный интервал для ожидаемого среднего значения заработной платы на уровне надежности  g = 0,99. Так, как среднее квадратическое отклонение не известно, то используем формулу

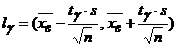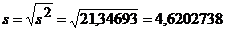, где . по таблице (см. приложение 3 в [10]) по заданным n=101  g = 0,99 находим tg=2,627.

Итак, 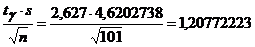 и доверительный интервал

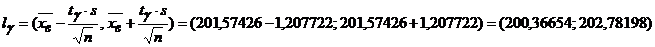б) вероятность того, что величина признака X у выбранного наугад из данной группы работника окажется в пределах от 196 у.е. до 202 у.е., найдем по формуле:

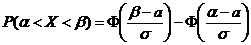, где а ≈ , a = 196, b = 202, s ≈ s=.4,6202738.

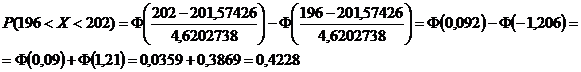
Ответ: Выборочная средняя ; выборочная дисперсия 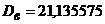; исправленная дисперсия s2=. .

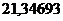С надёжностью 0,99 среднее значение а заработной платы работников банказаключено в доверительном интервале 200,37 < а < 202,78.

вероятность того, что величина признака X у выбранного наугад из данной группы работника окажется в пределах от 196 у.е. до 202 у.е., равна 0,42.

Дата добавления: 2018-04-05; просмотров: 2094; Мы поможем в написании вашей работы!

Поделиться с друзьями:


Мы поможем в написании ваших работ!
.
.
© 2014-2024 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.099)