РАСЧЕТ МАТРИЦЫ УЗЛОВЫХ ПРОВОДИМОСТЕЙ И МАТРИЦЫ КОНТУРНЫХ СОПРОТИВЛЕНИЙ
Найдем матрицу узловых проводимостей [  ] (без учета балансирующего узла) по формуле:
] (без учета балансирующего узла) по формуле:
|
|
|
|
Матрица узловых проводимостей [  ] (с учетом балансирующего узла) определяется по формуле:
] (с учетом балансирующего узла) определяется по формуле:
|
|
Матрица 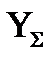 является вырожденной матрицей, т.е. нахождение для неё обратной не представляется возможным. Это подтверждается тем, что при суммировании элементов строк Y получается нулевая строка, и, следовательно, определитель этой матрицы, вычисленный по теореме разложения определителя по элементам строки (столбца ), обращается в 0, т.е . det
является вырожденной матрицей, т.е. нахождение для неё обратной не представляется возможным. Это подтверждается тем, что при суммировании элементов строк Y получается нулевая строка, и, следовательно, определитель этой матрицы, вычисленный по теореме разложения определителя по элементам строки (столбца ), обращается в 0, т.е . det 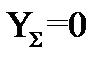
Матрица контурных сопротивлений находится из выражения:
|
|
СОСТАВЛЕНИЕ УЗЛОВЫХ УРАВНЕНИЙ УСТАНОВИВШЕГОСЯ РЕЖИМА ЭЛЕКТРИЧЕСКОЙ СЕТИ В МАТРИЧНОЙ ФОРМЕ И В АНАЛИТИЧЕСКОМ ВИДЕ ПРИ ЗАДАНИИ НАГРУЗОК В ТОКАХ.
1. Матричная форма записи:
Запишем первый закон Кирхгофа в матричной форме: 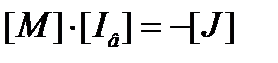 ,
,
где 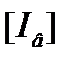 - вектор-столбец искомых токов ветвей;
- вектор-столбец искомых токов ветвей;
- 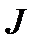 - вектор-столбец задающих токов узлов.
- вектор-столбец задающих токов узлов.
Токи ветвей можно найти как: 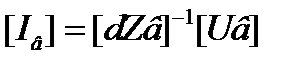
где 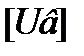 -матрица падений напряжений в ветвях,
-матрица падений напряжений в ветвях,
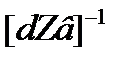 -матрица узловых проводимостей.
-матрица узловых проводимостей.
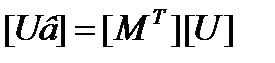 .
.
где 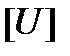 - матрица падений напряжения в узлах относительно БУ.
- матрица падений напряжения в узлах относительно БУ.
Полученные уравнения подставим в первый закон Кирхгофа:
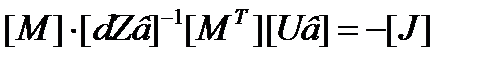
Обозначив 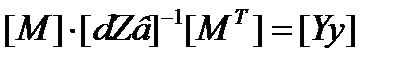 ,
,
где 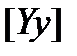 матрица собственных и взаимных узловых проводимостей, получим:
матрица собственных и взаимных узловых проводимостей, получим:
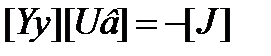 - система узловых уравнений в матричной форме.
- система узловых уравнений в матричной форме.
2. Аналитическая форма записи.
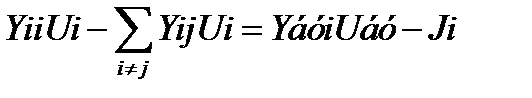 ,
,
где 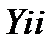 -собственные проводимости узлов,
-собственные проводимости узлов,
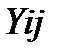 -взаимные проводимости узлов.
-взаимные проводимости узлов.
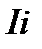 -ток нагрузки узла,
-ток нагрузки узла,
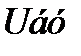 -напряжение балансирующего узла.
-напряжение балансирующего узла.
В результате записи уравнений для всех узлов, получим аналитическую форму записи:
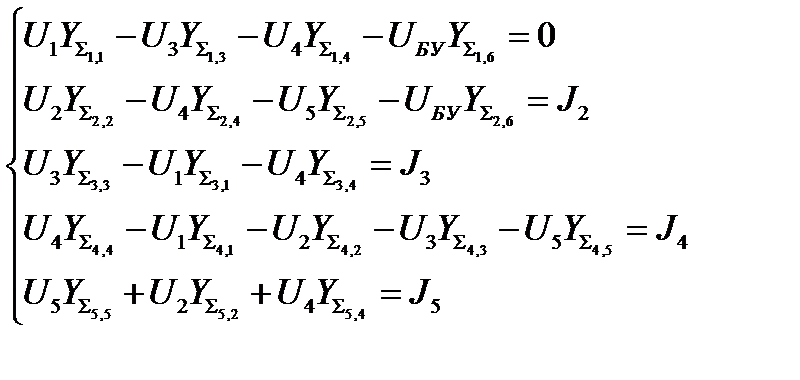
Решив полученную систему относительно U получим значения напряжений в узлах сети.
СОСТАВЛЕНИЕ КОНТУРНЫХ УРАВНЕНИЙ УСТАНОВИВШЕГОСЯ РЕЖИМА ЭЛЕКТРИЧЕСКОЙ СЕТИ НА ОСНОВЕ 2-ГО ЗАКОНА КИРХГОФА В МАТРИЧНОЙ ФОРМЕ И В АНАЛИТИЧЕСКОМ ВИДЕ ПРИ ЗАДАНИИ НАГРУЗОК В ТОКАХ.
1. Матричная форма записи:
Запишем первый закон Кирхгофа в матричной форме: 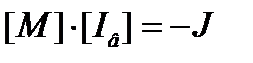 ,
,
Матрицу M, I представим в виде двух матриц : 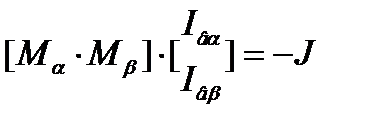
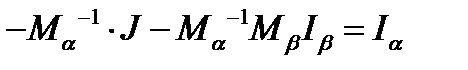
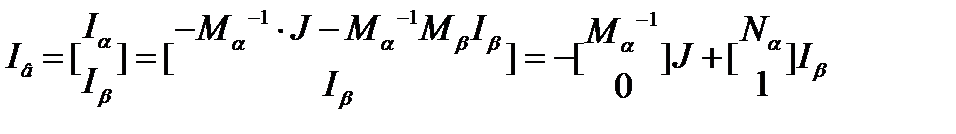
Запишем второй закон Кирхгофа в матричной форме: 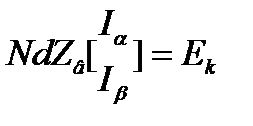
Из первого и второго закона получим:
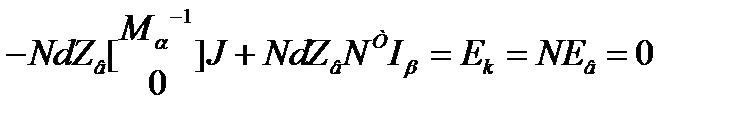
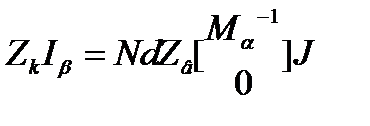 - контурное уравнение в матричной форме.
- контурное уравнение в матричной форме.
2. Аналитическая форма записи.
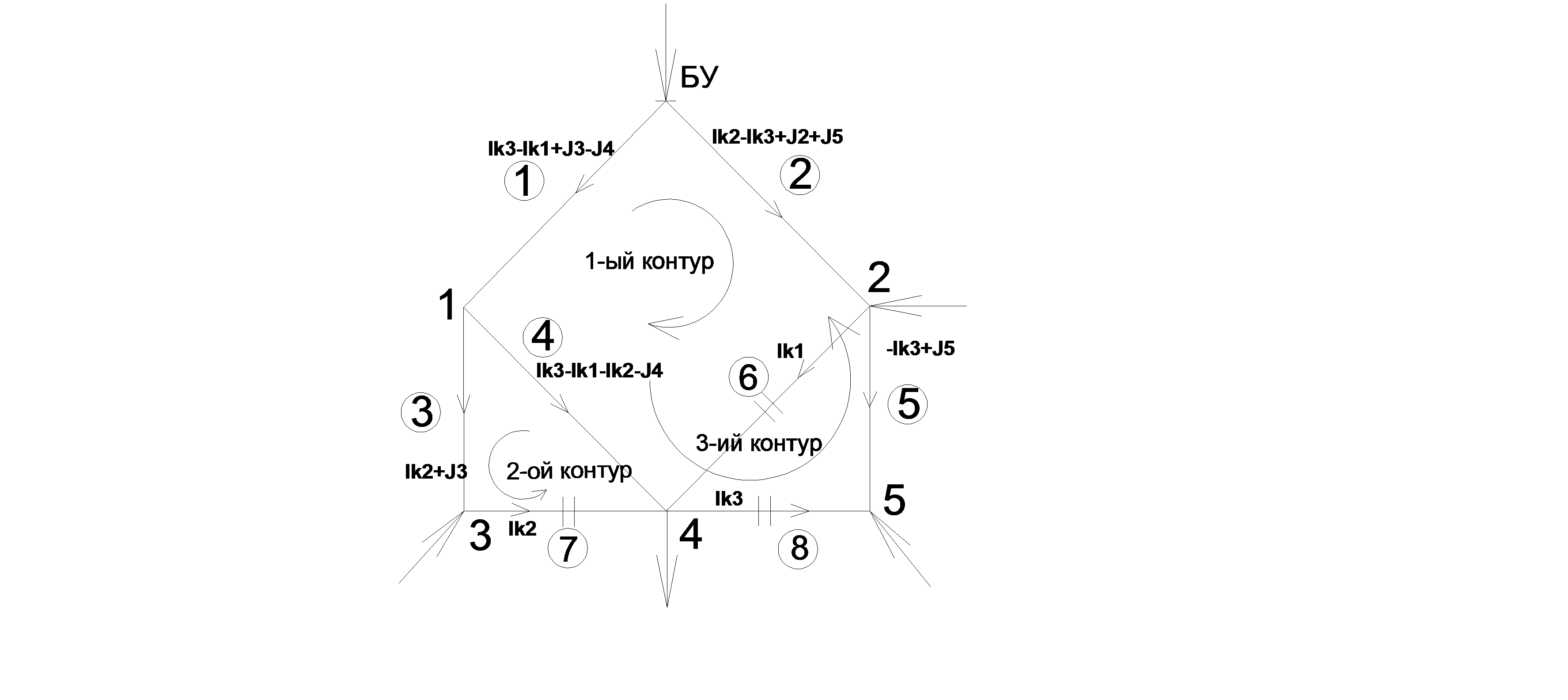
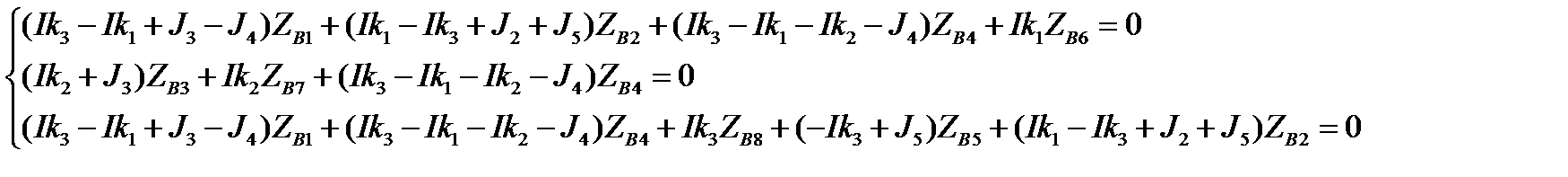
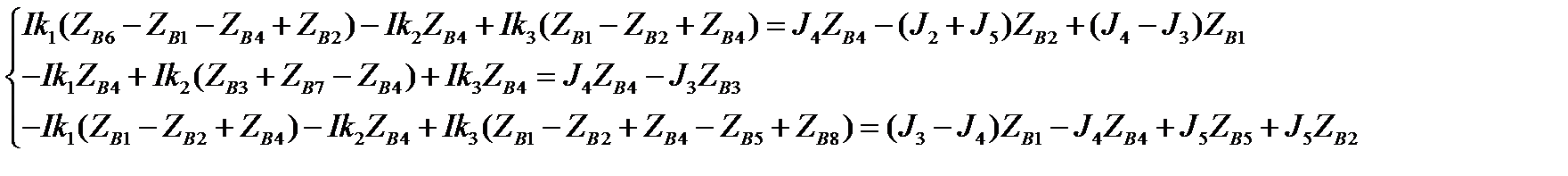
РАСЧЕТ РЕЖИМА ЭЛЕКТРИЧЕСКОЙ СЕТИ ПРИ ЗАДАНИИ НАГРУЗОК В ТОКАХ.
РАСЧЕТ РЕЖИМА ЭЛЕКТРИЧЕСКОЙ СЕТИ ПО УЗЛОВЫМ УРАВНЕНИЯМ.
Найдем матрицу задающих токов, по известным нагрузкам в узлах сети:
|
|
|
|
|
|
|
|
| |
| МВт Unom=110 кВ |
Где [n] - единичная матрица.
Найдем падение напряжения в узлах схемы относительно балансирующего узла:
|
|
Где [  ] - обратная матрица узловых проводимостей.
] - обратная матрица узловых проводимостей.
Напряжение в узлах схемы:
|
|
Где Uб - напряжение балансирующего узла, равное 115 к В.
Падение напряжения в ветвях схемы, токи в ветвях схемы:
|
|
|
|
Проверим, удовлетворяют ли полученные результаты условию:
|
|
|
|
Токи в ветвях найдены верно.
Найдем потокораспределение в ветвях схемы:
|
|
|
|
Представим матрицу Мт в виде двух составляющих матриц (М 1 и М 2) - для подтекающих и оттекающих ветвей.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дата добавления: 2018-04-05; просмотров: 485; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 См
См См
См
 кА
кА


 кВ
кВ кВ
кВ кВ
кВ кА
кА кА
кА кА
кА




 кВ
кВ кВ
кВ кВ
кВ кА
кА
 МВт
МВт МВт
МВт МВт
МВт МВт
МВт