Основные допущения метода совместного решения приближенных уравнений равновесия и пластичности

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Плоское напряженное состояние наиболее часто реализуется в операциях листовой штамповки (вытяжка, обжим, раздача и т.д.). Упрощенное уравнение равновесия рассмотрим на примере осесимметричной тонкостенной оболочки двойной кривизны.

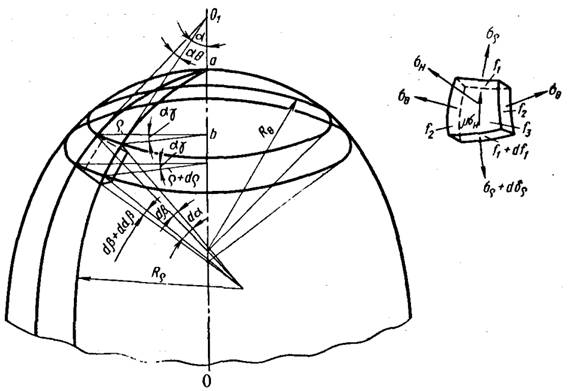
Рисунок 2 - Осесимметричная тонкостенная оболочка двойной кривизны.

Для вывода уравнения равновесия необходимо использовать следующие допущения:

1. Оболочка осесимметричная, поэтому все напряжения не зависят от координаты 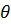, а касательные напряжения 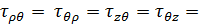0. Напряжение 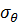— главное напряжение.

2. Принимаем что толщина заготовки постоянна и значительно меньше радиусов кривизны в меридиональном и широтном направлениях.

3. Размеры очага деформации вдоль срединой поверхности оболочки значительно больше толщины оболочки. При таких размерах характеристика очага деформации напряжения перпендикулярна к поверхности оболочки можно пренебречь. Тогда схема напряженного состояния с достаточной точностью может быть принята плоской.

4. Для тонкой оболочки у которой радиусы серединой поверхности значительно больше толщины оболочки, можно считать что по толщине оболочки постоянные. Если 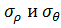постоянны по толщине оболочки, то их можно привести к серединным поверхностям оболочки.

5. Касательные напряжения вызванные трением на контактной поверхности оболочки можно учесть законом Амантона:

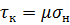где 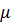- коэффициент трения;

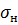- нормальное напряжение к срединной поверхности оболочки полученное

проектированием напряжений на нормаль к поверхности оболочки.

В большинстве операций листовой штамповки очаг деформации можно разделить на участки в каждом из которых кривизна срединных поверхностей оболочки в меридиональных сечениях постоянна.

3. Определение характера распределения нормальных напряжений на контактной поверхности заготовки.

Рассмотрим обжим цилиндрической заготовки в конической матрице. На рисунке 3 представлены схема деформирования заготовки в такой матрице и принятые обозначения размеров.

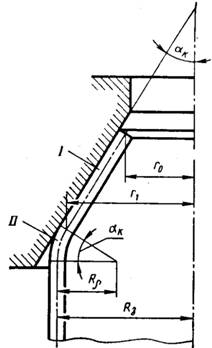
Рисунок 3 – схема деформирования заготовки в конической матрице.

Очаг деформации в этом случае состоит из двух участков: I, в котором заготовка соприкасается с конической полостью матрицы, и участка II свободного изгиба с радиусом срединной поверхности, в котором заготовка не соприкасается с матрицей.

Распределение напряжений в основном, коническом, участке очага деформации можно установить, подставляя значение из условия пластичности в уравнение 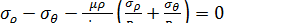и учитывая, что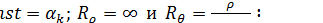

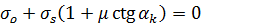Интегрируя это дифференциальное уравнение с разделимыми переменными, находим:

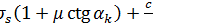Произвольную постоянную интегрирования C можно найти из граничного условия, согласно которому при (на крае заготовки) напряжение :

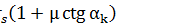Подставляя значение C в предыдущее уравнение, получаем формулу, которая позволяет установить распределение напряжений в коническом участке очага деформации:

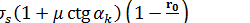Напряжение , действующее в коническом участке очага деформации на границе его с участком свободного изгиба, можно получить из формулы 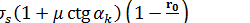при подстановке в нее значения (рисунок 3):

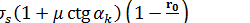Распределение напряжений на участке II очага деформации находим, решая уравнение 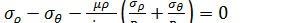, в котором принято (контакт заготовки с инструментом отсутствует). Получающееся дифференциальное уравнение имеет вид:

Интегрирование его дает уравнение:

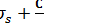При переходе элементов заготовки в процессе ее деформирования из участка II очага деформации в участок I радиус срединной поверхности в меридиональном сечении увеличивается от до бесконечности (спрямление), а при переходе из недеформируемой части заготовки в очаг деформации уменьшается от бесконечности до значения (изгиб). Считая, что изгиб и спрямление вызывают увеличение напряжения на , величина которого определяется по формуле , заключаем, что в качестве граничного условия для участка II очага деформации можно принять, что при , .

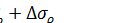Используя это граничное условие, находим:

;

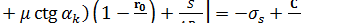отсюда произвольная постоянная интегрирования:

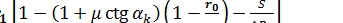Подставляя значение С в уравнение для определения величины в участке II очага деформации, получаем:

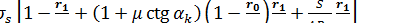Значение напряжения , действующего в участке II очага деформации на его границе с недеформируемой частью заготовки, определим по предыдущей формуле при подстановке в нее значения . Для упрощения в третьем и четвертом слагаемом примем :

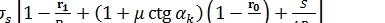Напряжение , действующее в стенках обжимаемой заготовки, с учетом влияния изгиба определим как сумму напряжения и приращения напряжения :

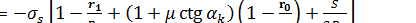. (1)

Для определения по формуле (1) при обжиме в конической матрице необходимо знать величину радиуса участка свободного изгиба. В первом приближении можно принять, что величина в участке II очага деформации определяется по формуле 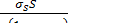, как в случае, когда меридиональное напряжение сравнительно велико:

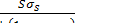. (2)

Подставляя значение из выражения (2) в (1), получаем:

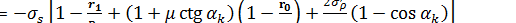. (3)

Подставляя значение из выражения 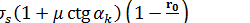в (3), после несложных преобразований получаем:

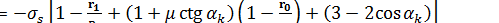. (4)

Так как при обжиме радиусы и незначительно отличаются по величине один от другого, то без большого ущерба для точности формулу (4) можно записать в несколько ином виде:

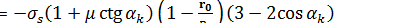. (5)

Формула (5) позволяет определить величину напряжения , действующего в стенках заготовки при обжиме в конической матрице.

Заметим, что этой формулой нельзя пользоваться для определения величины при обжиме в конической матрице, когда обжатая часть заготовки выходит в цилиндрическое отверстие матрицы, так как в этом случае появится новый участок очага деформации (на скругленной кромке матрицы), на границах которого элементы заготовки будут получать изгиб и спрямление [70].

Проведенный анализ обжима в конической матрице и в матрице с криволинейной образующей был выполнен без учета влияния упрочнения и изменения толщины заготовки в процессе деформирования на величину .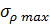

Дата добавления: 2018-04-05; просмотров: 758; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!