Распределение напряжений от сосредоточенной силы, действующей на полупространство

⇐ ПредыдущаяСтр 9 из 17Следующая ⇒

Рассмотрим действие сосредоточенной силы N, приложенной перпендикулярно к плоскости, ограничивающей полупространство. Этот случай является основным для получения решений, когда требуется установить распределение напряжений в массивах грунта при приложении различных нагрузок.

Решение этой задачи было получено в 1885г. французским ученым Ж. Буссинеском. Применение этого решения может иметь место при соблюдении следующих условий

( схема: из лекции №8 от 10.11.17г) :

1.грунты однородны и линейно деформируемы;

2.процесс сжатия в грунте закончился;

3.исследуемая точка расположена на значительном расстоянии от точки приложения силы.

Решение данной задачи для определения радиальных напряжений, полученное Буссинеском, имеет вид :

(формула: лекция 8 от 10.11.17г).

Как видно радиальные напряжения тем меньше, чем больше радиус R и чем больше будет полярный угол 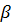. Наименьшие напряжения равные 0 следует ожидать на поверхности грунта при 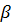= 90^о, а наибольшие напряжения будут у точек, расположенных при 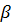= 0

Нормальная вертикальная составляющая напряжений в точке М может быть получена в виде проекции приведенного радиального напряжения на вертикальную ось: 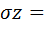(формула из лекции 8 от 10.11.17г).

Учитывая, что cosb =z/R — (где z - глубина расположения точки М),

получим решение задачи Буссинеска в виде:

=(формула: лекция 8 от 10.11.17г)

где к - табличный коэффициент, зависящий от отношения r/z.

Если на поверхности массива действует несколько сосредоточенных сил N\, N₂, N₃, то сжимающее напряжение в любой точке массива можно найти элементарным суммированием (т.е. по принципу суперпозиции):

= К1 (формула: лекция 8 от 10.11.17г)

тема 2: « Механика грунтов»

Вопрос 2.10Распределение напряжений от равномерно распределенной нагрузки, действующей по прямоугольной площадке.

Ответ:

Если на поверхности массива приложена местная равномерно распределенная нагрузка на площади ограниченных размеров, то напряжения в любой точке линейно деформируемого массива могут быть определены

суммированием напряжений возникших от системы сосредоточенных сил. Суммирование может быть выполнено точным и приближенным способом. Точный способ основан на замене распределенной нагрузки сосредоточенными силами, действующими по бесконечно малым площадкам, с последующим интегрированием по всей площадке загружения

dF = (формулы: лекция 8 от 10.11.17г)

dN =

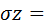
Интегрируя последнее выражение от 0 до l и от 0 до b можно определить напряжения в точке М от равномерно распределенной нагрузки:

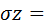(формула из лекции 8 от 10.11.17г)

Где l - длинная сторона прямоугольника; b - короткая сторона прямоугольника.

Угловые напряжения составляют 25% от напряжений под центром загруженной площадки.

тема 2: « Механика грунтов»

Вопрос 2.11Метод угловых точек

Ответ:

Суть метода заключается в том, что давление в любой точке массива грунта находят как суммарное давление угловых точек прямоугольных площадок на поверхности грунта, для этого фундамент в плане разбивают на прямоугольники, углы которых сходятся над исследуемой точкой.

Схема: (из лекции 8 от 10.11.17)

Для определения напряжений существует рабочие формулы

s_z₀=k_0*P₀ - если по центру;

s_zc=k_c_*P₀- под углом прямоугольника.

k₀ = (формула из лекции 8 от 10.11.17)

К_с =(формула из лекции 8 от 10.11.17)

тема 2: « Механика грунтов»

Вопрос 2.12Распределение напряжений под подошвой жестких фундаментов и штампов (контактная задача)

Ответ:

Если жёсткость тела, передающего нагрузку (например, фундамента), отлична от нуля, то под подошвой штампа распределение напряжений значительно отличается от равномерного.

Данная задача известна под названием контактной задачи. Ее решение в общем виде из-за математических трудностей ещё не получено. Имеются лишь некоторые частные решения, например, для жёсткого штампа с круглой подошвой основания:

Рx,y= (формула из лекции 9 от 17.11.17),

при =0; Рx, y = 0,5Р0

=r; Рx,y =

Результаты теоретических исследований показывают, что напряжения под краями штампа достигают бесконечно большой величины. Однако, как показывают непосредственные измерения, фактические напряжения под краями фундамента оказываются значительно больше теоретических, а сам вид эпюр напряжений в зависимости от величины нагрузки, размеров фундаментов и свойств грунтов может существенно отличаться от теоретического очертания. Таким образом, по подошве жёсткого фундамента (штампа) при центральной нагрузке эпюры распределения напряжений могут быть одного из трёх видов:

Pmax

1.Колоколообразные Pmax =(2 - 3,5) Po

Колоколообразная эпюра характерна для малых размеров фундамента, больших давлений и рыхлых грунтов.

Pmax

2.Параболические

Pmax = (1,3 - 1,7) Po

Параболическая эпюра характерна для средних размеров фундамента, средних давлений и среднесжимаемых грунтов.

Pmin

Pmax

3.Седлообразные

Pmin = (0,7 - 0,9)P0;

Pmax = (1,1 - 1.3) Р₀.

Седлообразная эпюра характерна для больших размеров фундамента, малых давлений и малосжимаемых грунтов.

Жесткость фундамента отражается на распределении напряжений в массиве грунта до глубины, равной ширине фундамента. На больших глубинах напряжения распределяются одинаково, независимо от жесткости фундамента.

В практике расчёта распределение напряжений по подошве жёстких фундаментов в большинстве случаев принимается линейным, в виде прямоугольных или трапецеидальных эпюр.

В случае центральной нагрузки напряжения по подошве фундамента определяются по формуле простого сжатия

s_z =N / A

где A - площадь подошвы фундамента.

нагрузки - по формуле сложного сопротивления

В случае внецентренного приложения нагрузки – по формуле сложного сопротивления:

s_z _max_,min₌(формула из лекции 9 от 17.11.17)

где W- момент сопротивления подошвы фундамента:

W= (формула из лекции 9, от 17.11.17)

е - эксцентриситет приложения нагрузки.

тема 2: « Механика грунтов»

Вопрос 2.13 Распределение напряжений в случае плоской задачи.

Задача Фламана

Ответ:

Если нагрузка распределена по бесконечной полосе, причем ее величина вдоль полосы (например, по оси Х) не меняется, то для оценки напряженного состояния массива достаточно исследовать распределение напряжений в любом сечении массива перпендикулярном этой оси. Такая задача называется плоской. Плоская задача имеет большое число практических приложений. Например: ленточные фундаменты под стенами зданий, основания подпорных стенок, насыпей плотин, дорожных полотен и т.п.

В плоской задаче приходится иметь дело только с тремя составляющими напряжений:

два нормальных напряжения:

- вертикальное _z ,

- горизонтальное у,

- и одно касательное напряжение .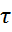

Решение этой задачи было получено Фламаном, на основе решения задачи о распределении напряжений от сосредоточенной силы.

Схема (из лекции 9 от 17.11.17)

Формулы для определения напряжений от линейной нагрузки имеют вид:

_z₌

у=

= (формулы из лекции 9 от 17.11.17)

тема 2: « Механика грунтов»

Вопрос 2.14 Распределение напряжений в грунте от равномерно распределенной нагрузки, действующей по гибкой полосе.

Ответ:

Для получения этого решения можно воспользоваться формулами для определения напряжений от линейной нагрузки. Нагрузка, приходящаяся на бесконечно малый элемент нагруженного участка, будет равна:

(формулы из лекции 9 от 17.11.17)

dN =

dy =

dl =

dN=

d _z=

Принимая элементарную нагрузку dN за сосредоточенную силу в условиях плоской задачи и интегрируя по ширине полосы, получим:

_z₌ (формула из лекции 9 от 17.11.17),

Где

II = (формула из лекции 9 от 17.11.17),

Значения коэффициента влияния K_z определяются по готовым таблицам в зависимости от относительных координат z/b и y/b.

тема 2: « Механика грунтов»

Вопрос 2.15 Графические изображения напряженного состояния грунтового массива.

Ответ:

Напряженное состояние массива грунта очень часто изображается и графически. Например, пользуясь вышеприведенными формулами легко построить эпюры распределения напряжений по горизонтальным и вертикальным сечениям массива грунта в случае плоской задачи. Эпюра представляет графическое изображение распределения напряжений по горизонтальным и вертикальным сечениям в массиве грунта.

Используя полученные эпюры напряжений можно построить и кривые равных напряжений, например, изобары, распоры, сдвиги.

Изобарой называется линия, представляющая геометрическое место точек в массиве грунта с равными вертикальными напряжениями.

Распором называется линия, представляющая геометрическое место точек в массиве грунта с равными горизонтальными напряжениями.

Сдвигами называются линии, представляющие геометрическое место точек в массиве грунта с равными касательными напряжениями.

По результатам изучения характера изобар и эпюр можно сделать следующие выводы:

1) Вертикальное давление в грунте по оси действия сосредоточенной силы с увеличением глубины уменьшается.

2)Вертикальное давление в грунте от действия сосредоточенной силы с увеличением глубины распространяется на большую площадь и становится равномернее.

3)Вертикальное давление в грунте в стороне от действия вертикальной силы на поверхности равно нулю и с увеличением глубины возрастает до некоторого предела, а затем уменьшается.

4) Из предыдущего вывода вытекает следствие, что под соседними фундаментами нужно проверять давление в грунте с учетом влияния нового фундамента.

Напряженное состояние в массиве в случае плоской задачи может также определяться через главные напряжения. Они характеризуют напряженное состояние в точке вне зависимости от ориентации площадок.

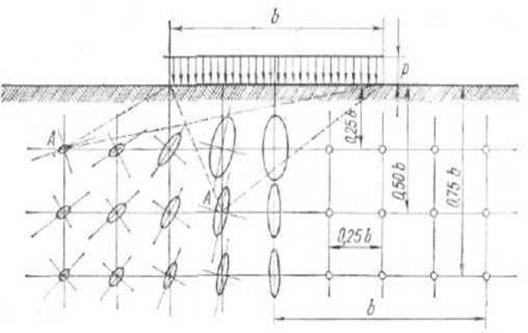
Главными напряжениями называются наибольшие и наименьшие нормальные напряжения, возникающие в рассматриваемой точке. Величины главных напряжений определяются по выражениям: для точки «А» (в пятне b) – , для точки «А» (вне пятна b) – « ».

Формулы для

               (формулы из лекции 10 от 24.11.17),

где а - угол видимости полосы в радианах.

Направление действия большего из главных напряжений совпадает с биссектрисой угла видимости. На величинах главных напряжений как полуосях можно построить эллипсы напряжений, наглядно характеризующие напряженное состояние массива.

тема 2: « Механика грунтов»

Вопрос 2.16 Распределение напряжений от собственного веса грунта (природное давление)

Ответ:

Вертикальные давления, возникающие в грунтовом массиве от собственного веса грунта, возрастают пропорционально глубине рассматриваемого слоя. В соответствии с этим эпюра напряжений по глубине однородного слоя грунта будет иметь вид треугольника, а при нескольких неоднородных слоях изобразится ломаной линией.

Вертикальное давление на глубине z будет равно:

zgi = (формула из лекции 10 от 24.11.17)

где n - число разнородных грунтовых напластований;

Yi - удельный вес грунта в i-ом слое, кН/м,куб ;

h_i - толщина i-го слоя грунта, м.

Например, для рассмотренного разреза:

zg1=

zg2 =

zg3 = (формулы из лекции 10 от 24.11.17)

В слоях, расположенных ниже уровня грунтовых вод, удельный вес грунта водопроницаемых грунтов принимается уменьшенной за счет взвешивающего действия воды: g_s_b = (формулы из лекции 10 от 24.11.17)

где g_s - удельный вес частиц грунта; е- коэффициент пористости грунта.

Тогда s_zg4=s_zg3+g_sb3 h_3/2

При наличии слоя водонепроницаемого грунта (например, глины в твердом и полутвердом, суглинки в твердом состоянии) который является водоупором, давление на его кровле будет складываться из давления грунта и гидростатического давления столба воды

s_zg₅=s_zg₄+s_W=s_zg₄+g_W h_W

s_zg6=s_zg5+g₄ h₄

тема 2: « Механика грунтов»

Вопрос 2.17Теория предельного равновесия.

                 Фазы деформации грунтов под нагрузкой и их физические причины.

Ответ:

О

                                                    P

S                                      D

Исследования деформативности грунтов при штамповых испытаниях позволили прийти к следующим выводам:

1)Грунт не является упругим материалом. Остаточные деформации грунта, как правило, больше упругих.

2)Грунту не свойственна строгая линейная зависимость между напряжениями и деформациями.

По мере увеличения давления на основание последовательно развиваются 3 фазы деформации.

I фаза - фаза уплотнения; II фаза - фаза сдвигов; III фаза - фаза разрушения.

Участок ОА соответствует нагрузке, в пределах которой напряжение под штампом не превышает структурной прочности (P_str).

Участок АВ характеризуется следующими особенностями:

1) зависимость между давлениями и деформациями близка к прямолинейной;

2) осадка происходит за счет вертикальных перемещений частиц;

3) осадки происходят за счет уменьшения пористости, т.е. уплотнения грунта.

Участок ВС. Деформации возрастают быстрее, чем вызывающие ее давления. Приращение осадки происходит за счет горизонтальных и вертикальных перемещений частиц.

Участок СД. Осадка происходит за счет перемещения частиц грунта из под фундамента в сторону и даже вверх и наступает полное разрушение грунта основан

тема 2: « Механика грунтов»

Вопрос 2.18 Сущность теории предельного равновесия.

                Характерные виды давления на основание.

                   Ответ:

Устойчивость грунтовых оснований, грунтовых массивов и сооружений изучается в условиях их предельного напряженного состояния, когда малейшее увеличение действующих усилий вызывает потерю устойчивости грунта. Потеря устойчивости в какой-либо точке грунта произойдет в том случае, если напряжение в ней превысит полное предельное сопротивление грунта сдвигу и возникнут площадки скольжения.

- если грунт сыпучий

t_a £s_a tg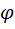

(если условие выполняется, то сохраняется устойчивость)

если грунт связный

t_a £s_a tg 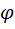+C

В начале второй фазы зоны предельного равновесия формируются около краев грунта ,где максимальное значение имеет сдвигающее напряжение.

I



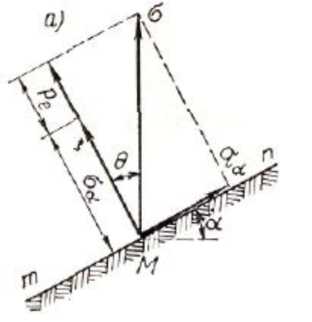
(примеч.: На схеме вертикальный угол- 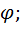сдвигающее напряжение по уклону-t_a ₎

                                               P

S                                      D

При увеличении давления на фундамент эти зоны получают все больше распространение. После того, как они получат полное развитие, возникает деформационное ядро и при дальнейшем увеличении нагрузки в грунте образуются поверхности скольжения, выходящие за пределы подошвы фундамента и наступает фаза прогрессирующего течения. Давление, при котором в грунте преобладает деформационное уплотнение и не возникает зон сдвигов, называется начальным критическим давлением.

тема 2: « Механика грунтов»

Вопрос 2.19 Сущность теории предельного равновесия.

Характерные виды давления на основание. Предельное давление.

                   Ответ:

Давление, при котором возникают фазовые выпирания грунта из под фундамента, называется предельным давлением. Такое давление не допустимо ни под одним сооружением. Такое значение давления принимают за сопротивление грунта. Как показала практика, при давлении Р=Р_кр в грунтах основания имеется некоторый резерв несущей способности. Следовательно, расчетное сопротивление грунта можно принимать равным или несколько превышающим это значение.

Величины Р_кр и Р_пр можно определить на основании теории предельного напряжённого состояния:

Р_кр = (формула из лекции 10 от 24.11.17),

Где:

h - глубина заложения фундамента;

- удельный вес грунта;

С - удельное сцепление грунта;

z_max - максимальная ордината области предельного равновесия в грунте основания.

Допускается, чтобы величина Ркр под подошвой фундамента определялась при развитии области предельного равновесия, равной 0,25 ширины фундамента (величина z_max =0,25b). Давление, соответствующее этому называется нормативным сопротивлением грунта:

RН =(формула из лекции 10 от 24.11.17)

Расчётное сопротивление R определяется как из условия устойчивости грунтов, так и из условия прочности и устойчивости здания и сооружения введением дополнительных коэффициентов, учитывающих особенности взаимной работы основания сооружения:

R = (формула из лекции 11от 01.12.17)

где _с и _с₂ - коэффициенты условий работы;

к - коэффициент, принимаемый равным 1, если и С определены лабораторным путём, и принимается 1,1, если и С приняты по таблицам СП; b - ширина подошвы фундамента;

- осредненное значение удельного веса грунтов, залегающих ниже

подошвы фундамента кН/м,куб ;

II - то же, залегающих выше подошвы фундамента, кН/м,куб ;

d1 - глубина заложения фундамента бесподвальных сооружений от уровня планировки или приведённая глубина заложения наружных и внутренних фундаментов от пола подвала;

db - высота подвала;

М M_q, M_c - табличные коэффициенты, принимаемые в зависимости от угла внутреннего трения грун

тема 2: « Механика грунтов»

Вопрос 2.20Устойчивость грунтовых откосов и склонов. Основные положения.

Ответ:

Откосом называется искусственно созданная поверхность, ограничивающая природный грунтовый массив, выемку или насыпь.

Склоном называется откос, образованный природным путем.

Встречаются следующие основные виды разрушения откосов и склонов: оползни, обвалы, оплывы, выдавливание.

Наиболее частыми нарушениями земляных откосов являются оползни. Различают следующие виды оползней:

1.Оползень вращения с возникающими криволинейными поверхностями обрушения.

2.Оползень скольжения по зафиксированной поверхности (когда слабый грунт лежит на наклонном склоне плотного или скального грунта).

3.Оползень разрушения (когда грунты, переносимые водой, текут в виде грязевых потоков).

Основные причины нарушения устойчивости откосов:

1) Устранение естественной опоры массива грунта вследствие разработки котлованов, подмыва откоса.

2) Увеличение внешней нагрузки на откос.

3) Устройство недопустимо крутого откоса.

4) Увеличение удельного веса грунта в призме обрушения в результате заполнения пор водой.

5) Влияние взвешивающего действия воды на грунт в основании.

6) Увеличение гидродинамического действия воды, выходящей через поверхность откоса.

7) Снижение сцепления и трения грунта при его увлажнении. Увлажнение грунта, вызванное вследствие разрыхления котлована при его промерзании и оттаивании.

8) Динамическое воздействие при движении транспорта, забивании свай или сейсмических сил.

тема 2: « Механика грунтов»

Вопрос 2.21 Устойчивость откоса в идеально сыпучих грунтах.

                Ответ:

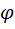- угол внутреннего трения «не» равняется 0; С - удельное сцепление грунта =0;

                                                      С

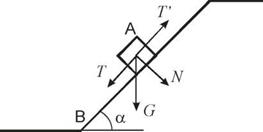
Рассмотрим устойчивость частицы А, на отрезке откоса ВС. Вес частицы F разложим на 2 составляющие: N, нормальную к поверхности откоса, и T, касательную к ней.

Кроме того, на частицу действует сила трения Т'.

В таком случае:….. N, T, Т «прим» = (формулы: лекция 11 от 01.12.17)

Составим уравнение проекций сил на направление поверхности откоса ВС, в условиях предельного равновесия

T – T^' = 0.

Подставляя в уравнение все неизвестные и деля на G cos _a , получим:

(формула: лекция 11от 01.12.17), отсюда:

tg - tg 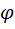₌_0;_{отсюда:} .

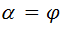Таким образом, предельный угол откоса идеально сыпучего грунта равен углу внутреннего трения этого грунта. Этот угол носит название угла естественного откоса.

тема 2: « Механика грунтов»

Вопрос 2.22 Устойчивость вертикального откоса в идеально связанных грунтах.

Ответ:

угол внутреннего трения = 0; С - удельное сцепление грунта «не» равняется 0.

Пылеватые глинистые грунты часто обладают малым углом внутреннего трения, который при приближенном решении можно не учитывать. В то же время эти грунты имеют сцепление, благодаря которому и выдерживается вертикальный откос. Для строителей при отрывке котлована важно знать на какую глубину можно разрабатывать грунт с вертикальным откосом без его крепления.

Схема: (лекция 11 от 01.12.17)

Рассмотрим устойчивость вертикального откоса АВ высотой h. Проведем поверхность обрушения под углом и разобьем призму обрушения на вертикальные элементы шириной dy. Вес крайнего элемента шириной dy будет равен:

(формула: лекция 11 от 01. 12.17)

Сдвигающая сила по наклонной площадке составит :

(формула: лекция 11 от 01. 12.17)

где dy - ширина элемента, h - высота, у - удельный вес грунта.

Удерживающая сила на этом участке обусловлена только удельной силой сцепления :

(формула: лекция 11 от 01. 12.17)

Составим уравнение проекций сил на линию АС, в условиях предельного равновесия

dT - dT' = 0.

Высота вертикального откоса при этом может быть определена как:

h =( формула: лекция 11 от 01.12.17.)

Худшие условия устойчивости будут при угле внутреннего трения = 45⁰ (sin 2*45° = 1). Поэтому максимально возможная высота вертикального откоса без крепления составит: h = (формула: лекция 11 от 01.12.17)

тема 2: « Механика грунтов»

Вопрос 2.23Метод круглоцилиндрических поверхностей скольжения

Ответ:

При проектировании откосов высотой более 12 м следует проверять расчетом их устойчивость. Наблюдения показали, что откосы обрушиваются по поверхностям, близким к круглоцилиндрическим.

Шведский инженер В.Феллениус разработал метод расчета, в основе которого лежит статический расчет устойчивости отдельных вертикальных элементов массы грунта, ограниченных сверху поверхностью грунта, а снизу - круглой дугой скольжения.

Считается, что потеря устойчивости откоса может произойти в результате вращения этого грунтового массива относительно некоторого центра О. Поверхность скольжения принимается проходящей по дуге окружности с радиусом R.

Для нахождения действующих сил сдвигающийся массив разбивают на вертикальные отсеки. Нагрузку от веса каждого отсека Pi

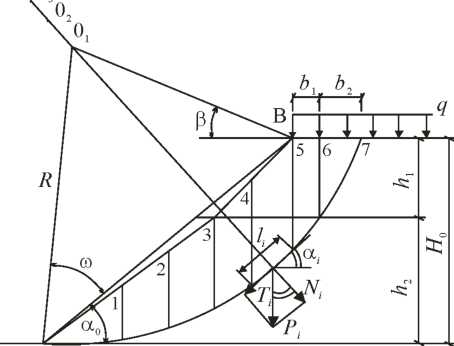
A

переносят в уровень его основания, где эту силу раскладывают на нормальную N_i и касательную T_i к поверхности скольжения.

Суть метода заключается в определении центра вращения с минимальным коэффициентом запаса устойчивости ку.   Коэффициент устойчивости может быть найден как соотношение суммы моментов всех сил, удерживающих основание (М_уд) относительно центра вращения О, к сумме моментов всех сил, сдвигающих (вращающих) основание (М_сдв) относительно того же центра, т.е:

ку = (формула: лекция 11 от 01.12.17)

Поскольку необходимо определить минимальный коэффициент устойчивости, намечают ряд центров вращения О1, О₂, ... , О_п и производят расчет для соответствующих поверхностей скольжения.

Считается, что устойчивость откоса обеспечена, если ку > 1,2.

Практика показала, что метод В.Феллениуса приводит к некоторому запасу прочности. К сожалению, метод круглоцилиндрических поверхностей скольжения не дает возможности запроектировать откос с заранее заданным коэффициентом устойчивости.

тема 2: « Механика грунтов»

Вопрос 2.24 Давление грунта на подпорные стенки. Виды подпорных стен

Ответ:

Подпорные стены предназначены для защиты от обрушения откосов насыпей и выемок различного назначения, естественных склонов. Берегоукрепительные стены, набережные, стены рамп, каналов - все это примеры применения подпорных стен.

По материалу подпорные стены подразделяются на каменные, бутобетонные, бетонные и железобетонные.

В зависимости от принятого конструктивного решения подпорные стены могут быть массивными, тонкими и комбинированными.

Массивные подпорные стены:

Устойчивость массивных стен от воздействия активного давления грунта обеспечивается в основном их собственным весом.

Устойчивость тонких стен обеспечивается в основном весом грунта, вовлекаемого конструкцией в работу.

Тонкие подпорные стены:

Дата добавления: 2018-04-05; просмотров: 2820; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒

Мы поможем в написании ваших работ!