Побудова економіко-математичної моделі
Позначимо через х1, х2, х3, х4 масу (в кг) м’яса, борошна, молока і цукру відповідно.
Сумарна маса продуктів має не перевищувати 35 кг:
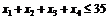 ,
,
а об’єм, який вони мають займати, — не більше 45 дм3:
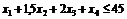 .
.
Крім того, мають виконуватися співвідношення стосовно пропорцій за масою продуктів:
а) м’яса принаймні удвічі більше, ніж борошна, отже:
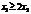 ;
;
б) борошна не менше, ніж молока: 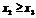 ;
;
в) молока хоча б у вісім разів більше, ніж цукру: 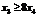 .
.
Калорійність всього набору продуктів можна визначити так:
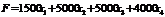 .
.
Отже, економіко-математична модель задачі має вигляд:
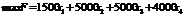
за умов:
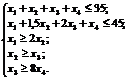
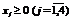 .
.
Розв’язуючи задачу отримуємо такий оптимальний план: х1=16, х2=8, х3=8, х4=1. Цільова функція дорівнює:
max F = 1500*16+5000*8+5000*8+4000*1 = 108000 (ккал/кг)
Отже, для того, щоб сумарна калорійність продуктів була найбільшою, складала 108000 ккал/кг до рюкзаку треба покласти 16 кг мяса, 8 кг борошна, 8 л молока та 1 кг цукру.
2. Симплексним методом знайти розв’язок задачі лінійного програмування

Розв’язання
Застосуємо алгоритм симплекс-методу:
1. min Z = x1 +5x2 + 3x3 -Мx4;
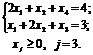
2. Векторна форма запису системи обмежень має вигляд:
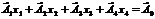 ,
,
де  ,
,  ,
, 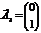 ,
, 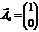 ,
, 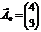 .
.
У цій задачі х3 та х4 — базисні змінні, а х1, х2 — вільні. Нехай х1 = х2 = 0, тоді х3 = 3; х4 = 4.
Перший опорний план задачі:
X0 = (0; 0; 3; 4), Z0 = 9-4М.
4. Подальше розв’язування прямої задачі подано у вигляді симплексної таблиці: q Zj – сj ³
|
|
|
0Сбаз
| Базис | Сбаз | План | 1 | 5 | 3 | -М | q |
| х1 | х2 | х3 | х4 | ||||
| Х4 | -М | 4 | 2 | 1 | 0 | 1 | 2 |
| Х3 | 3 | 3 | 1 | 2 | 1 | 0 | 3 |
| Zj – сj ³ 0 | -4М | -2М | -М | 0 | 0 |
| |
|
| 1 | 2 | 1 | 1/2 | 0 | 1/2 | |
|
| 3 | 1 | 0 | 1,5 | 1 | 1/2 | |
| Zj – сj ³ 0 | 5 | 0 | 0 | 0 | 2 |
| |
Оскільки всі 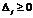 , то з останньої симплекс-таблиці оптимальним планом задачі є вектор:
, то з останньої симплекс-таблиці оптимальним планом задачі є вектор:
Х* = (2; 0; 3; 0),
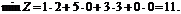
!!!!!!!!!!!!!Білет №22!!!!!!!!!!!!
Фермерське господарство спеціалізується на вирощуванні озимої пшениці і має три ділянки землі площею S1 = 40 га, S2 = 90 га, S3 = 55 га. Враховуючи наявну кількість посівного матеріалу, є можливість засіяти всю площу озимою пшеницею трьох сортів. Кількість пшениці сорту «Миронівська-808» забезпечить посів на 80 га, «Безоста-1» – 60 га та «Одеська-51» – 45 га. Урожайність сорту «Миронівська-808» на даних ділянках становить відповідно 41 ц/га, 40 ц/га, 46 ц/га. Аналогічно для сорту «Безоста-1» маємо: 38 ц/га, 41 ц/га, 45 ц/га, а для «Одеської-51» – 30 ц/га, 28 ц/га, 40 ц/га. Необхідно розподілити посівний матеріал за земельними ділянками так, щоб отримати максимальний урожай (валовий збір) озимої пшениці. Побудувати економіко-математичну модель задачі.
Побудова економіко-математичної моделі.
Позначимо через хij площу (га) і-ої земельної ділянки, що буде засіяна j-м сортом озимої пшениці (сорти «Миронівська-808», «Безоста-1», «Одеська-51» відповідатимуть номерам 1, 2, 3), (і = 1, 2, 3), (j = 1, 2, 3).
|
|
|
Тоді використання земельних угідь описуватиме така система обмежень:
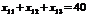 ;
;
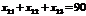 ;
;
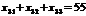 .
.
Використання посівного матеріалу формально можна описати так:
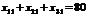 ;
;
 ;
;
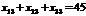 .
.
Валовий збір зерна розраховується як сума добутків урожайностей відповідних сортів пшениці на їх посівні площі, тобто:
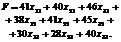
Отже, економіко-математична модель задачі загалом буде мати вигляд:
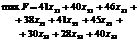
за умов:
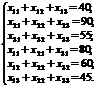
Оптимальний розподіл посівного матеріалу за земельними ділянками:
| Земельна ділянка | x1 | x2 | x3 | площа, га |
| Сорт насіння | ||||
| c1 | 40 | 0 | 0 | 40 |
| c2 | 30 | 60 | 0 | 90 |
| c3 | 10 | 0 | 45 | 55 |
| посівний матеріал, га | 80 | 60 | 45 |
|
Цільова функція, тобто максимальний урожай (валовий збір) озимої пшениці за даного розподілу посівного матеріалу за ділянками дорівнює:
max F = 40*41+30*40+10*46+60*41+45*40 = 7560 (ц/га)
2. Побудувати двоїсту задачу до заданої задачі лінійного програмування. Визначити оптимальні плани прямої та двоїстої задач.
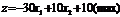
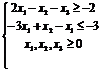 Розв’язання:
Розв’язання:
Перш ніж записати двоїсту задачу, необхідно пряму задачу звести до стандартного вигляду. Оскільки цільова функція F максимізується і в системі обмежень є нерівності, то вони мусять мати знак « 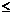 ». Тому перше обмеження задачі помножимо на (–1). Після цього знак нерівності зміниться на протилежний. Отримаємо:
». Тому перше обмеження задачі помножимо на (–1). Після цього знак нерівності зміниться на протилежний. Отримаємо:
|
|
|
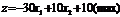
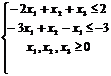
Тепер за відповідними правилами складемо двоїсту задачу:

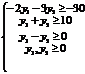
Оскільки записані задачі симетричні, то будь-яку з них можна розв’язати симплекс-методом. Наприклад, визначимо спочатку оптимальний план прямої задачі. Для цього застосуємо алгоритм симплекс-методу.
1. max Z = – 30x1 + 10x2 + 0x3 + 0x4+0 x5 +10;
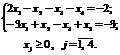
2. Векторна форма запису системи обмежень має вигляд:
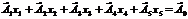 ,
,
де 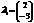 ,
, 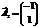 ,
, 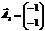 ,
, 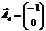 ,
,  ,
, 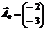 .
.
У системі векторів для утворення початкового одиничного базису відсутній один вектор. Тому введемо штучну змінну в перше обмеження.
3. Розширена задача лінійного програмування буде такою:
max Z = – 30x1 + 10x2 + 0x3 + 0x4+0 x5 – Мx6+10;
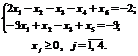
У цій задачі х6 та х5 — базисні змінні, а х1, х2, х3 х4— вільні. Нехай х1 = х2 = х3 = х4= 0, тоді х6 = -2; х5 = -3.
Перший опорний план задачі:
X0 = (0; 0; 0; 0; -3; -2), Z0 = – M+10.
4. Подальше розв’язування прямої задачі подано у вигляді симплексної таблиці:
Білет №23
1. Фірма спеціалізується на виробництві офісних меблів, зокрема вона випускає два види збірних книжкових полиць – А та В. Полиці обох видів виготовляють на верстатах 1 та 2. Тривалість обробки деталей однієї полиці кожної моделі подано в табл. 1.
|
|
|
Таблиця 1 – Тривалість виготовлення книжкових полиць
| Верстат | Тривалість обробки | Ресурс робочого часу верстатів, год. на тиждень | |
| А | В | ||
| 1 | 30 | 15 | 40 |
| 2 | 12 | 26 | 36 |
Прибуток фірми від реалізації однієї полиці моделі А дорівнює 50 у. о., а моделі В – 30 у. о. Вивчення ринку збуту показало, що тижневий попит на книжкові полиці моделі А ніколи не перевищує попиту на модель В більш як на 30 одиниць, а продаж полиць моделі В не перевищує 80 одиниць на тиждень.
Необхідно визначити обсяги виробництва книжкових полиць цих двох моделей, що максимізують прибуток фірми. Для цього слід побудувати економіко-математичну модель поставленої задачі.
Побудувати економіко-математичну модель задачі.
Побудова математичної моделі. Змінними в моделі є тижневі обсяги виробництва книжкових полиць моделей А та В. Нехай х1 — кількість полиць моделі А, виготовлених фірмою за тиждень, а х2 — кількість полиць моделі В. Цільова функція задачі — максимум прибутку фірми від реалізації продукції. Математично вона подається так:
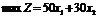 .
.
Обмеження задачі враховують тривалість роботи верстатів 1 та 2 для виготовлення продукції та попит на полиці різних моделей.
Обмеження на тривалість роботи верстатів 1 та 2 мають вид:
для верстата 1:
30х1 + 15х2 ≤ 2400 (хв);
для верстата 2:
12х1 + 26х2 ≤ 2160 (хв).
Обмеження на попит записуються так:
х1 – х2 ≤ 30 та х2 ≤ 80.
Загалом економіко-математичну модель цієї задачі можна записати так:
max Z = 50х1 + 30х2
за умов:
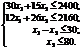
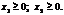
|
Ця економіко-математична модель є моделлю задачі лінійного програмування, що містить лише дві змінні, і тому може бути розв’язана графічно.
Розв’язання. Перший крок згідно з графічним методом полягає в геометричному зображенні допустимих планів задачі, тобто у визначенні такої області, де водночас виконуються всі обмеження моделі. Замінимо знаки нерівностей на знаки строгих рівностей і побудуємо графіки відповідних прямих. Кожна з побудованих прямих поділяє площину системи координат на дві півплощини. Координати точок однієї з півплощин задовольняють розглядувану нерівність, а іншої — ні. Щоб визначити необхідну півплощину, потрібно взяти будь-яку точку і перевірити, чи задовольняють її координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності. Інакше таким зображенням є інша півплощина.
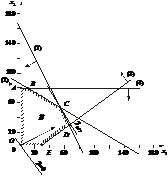
Умова невід’ємності змінних х1 ≥ 0, х2 ≥ 0 обмежує область допустимих планів задачі першим квадрантом системи координат. Переріз усіх півплощин визначає область допустимих планів задачі — шестикутник OABCDE. Координати будь-якої його точки задовольняють систему обмежень задачі та умову невід’ємності змінних. Тому поставлену задачу буде розв’язано, якщо ми зможемо відшукати таку точку багатокутника OABCDE, в якій цільова функція Z набирає найбільшого значення.
Для цього побудуємо вектор 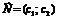 , координатами якого є коефіцієнти при змінних у цільовій функції задачі. Вектор
, координатами якого є коефіцієнти при змінних у цільовій функції задачі. Вектор 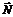 завжди виходить із початку координат і напрямлений до точки з координатами (х1 = с1; х2 = с2). У нашій задачі вектор
завжди виходить із початку координат і напрямлений до точки з координатами (х1 = с1; х2 = с2). У нашій задачі вектор 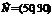 . Він задає напрям збільшення значень цільової функції Z, а вектор, протилежний йому, — напрям їх зменшення.
. Він задає напрям збільшення значень цільової функції Z, а вектор, протилежний йому, — напрям їх зменшення.
Побудуємо лінію, що відповідає, наприклад, значенню Z = 0. Це буде пряма 50х1 + 30х2 = 0, яка перпендикулярна до вектора  і проходить через початок координат. Оскільки в даному прикладі необхідно визначити найбільше значення цільової функції, то пересуватимемо пряму 50х1 + 30х2 = 0 паралельно самій собі згідно з напрямом вектора
і проходить через початок координат. Оскільки в даному прикладі необхідно визначити найбільше значення цільової функції, то пересуватимемо пряму 50х1 + 30х2 = 0 паралельно самій собі згідно з напрямом вектора 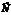 доти, доки не визначимо вершину багатокутника, яка відповідає оптимальному плану задачі.
доти, доки не визначимо вершину багатокутника, яка відповідає оптимальному плану задачі.
Із рис. 2.14 видно, що останньою спільною точкою прямої цільової функції та багатокутника OABCDE є точка С. Координати цієї точки є оптимальним планом задачі, тобто такими обсягами виробництва книжкових полиць видів А та В, що забезпечують максимум прибутку від їх реалізації за даних умов.
Координати точки С є розв’язком системи рівнянь:
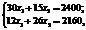
звідси маємо: х1 = 50; х2 = 60.
Отже, Х* = (50; 60); 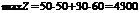
Це означає, що коли фірма щотижня виготовлятиме 50 збірних книжкових полиць моделі А та 60 — моделі В, то вона отримає максимальний прибуток — 4300 у. о. Це потребуватиме повного використання тижневих ресурсів робочого часу верстатів 1 та 2.
2. Розв’язати задачу опуклого програмування.
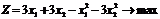
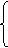

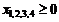 .
.
Розв’язання. Оскільки цільова функція виражена сумою лінійної функції 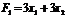 та квадратичної форми
та квадратичної форми 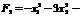
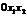 , а система обмежень є лінійною, то маємо задачу квадратичного програмування.
, а система обмежень є лінійною, то маємо задачу квадратичного програмування.
Визначимо вид квадратичної форми 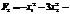
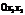 , для чого відшукаємо корені характеристичного рівняння, що відповідає матриці, складеній з коефіцієнтів при змінних даної функції:
, для чого відшукаємо корені характеристичного рівняння, що відповідає матриці, складеній з коефіцієнтів при змінних даної функції:
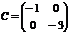 .
.
Характеристичним рівнянням для матриці С буде:
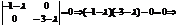

Оскільки обидва корені характеристичного рівняння від’ємні, то квадратична форма 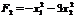 є від’ємно означеною, а отже, опуклою.
є від’ємно означеною, а отже, опуклою.
Запишемо функцію Лагранжа для цієї задачі:
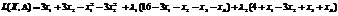 .
.
Скористаємося теоремою 8.4. Необхідні умови існування екстремуму матимуть вигляд:
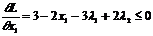 , причому
, причому 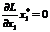 ;
;
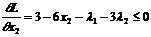 , причому
, причому 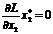 ;
;
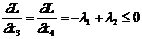 , причому
, причому 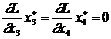 ;
;
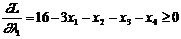 , причому
, причому 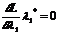 ,
,
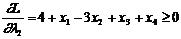 , причому
, причому 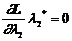 ,
,
де 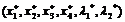 — координати сідлової точки.
— координати сідлової точки.
Обмеження, що відповідають нерівностям, запишемо у вигляді:
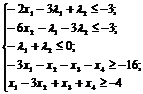
Вводимо додаткові змінні для зведення нерівностей до
рівнянь:
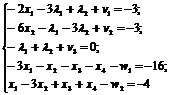
Для зведення задачі до канонічної форми помножимо кожне рівняння на (–1):
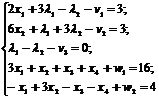
Очевидно, що в даному разі штучні змінні необхідно вводити в перші три рівняння. У четвертому та п’ятому рівняннях базисними змінними будуть 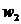 ,
, 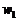 . Маємо таку задачу лінійного програмування:
. Маємо таку задачу лінійного програмування:
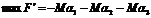 ,
,
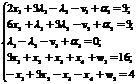
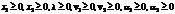 .
.
Розв’язавши її симплексним методом, отримаємо:
!!!!!!!!!!!!!!!Білет №24!!!!!!!!!!!!!!!!
1. Для невеликої птахоферми потрібно розрахувати оптимальний кормовий раціон на 1000 курчат, яких вирощують з 4-х до 8-тижневого віку. Нехтуючи тим, що потижневі витрати кормів для курчат залежать від їхнього віку, вважатимемо, що за 4 тижні курча споживає не менше 500 г суміші. Крім цього, кормовий раціон курчат має задовольняти певні вимоги щодо поживності. Сформулюємо ці вимоги у спрощеному вигляді, беручи до уваги лише дві поживні речовини: білок і клітковину, що містяться у кормах двох видів – зерні та соєвих бобах. Вміст поживних речовин у кожному кормі та їх вартість маємо у табл. 1.
Таблиця 1 – Поживність та вартість кормів
| Корм | Вміст поживних речовин в 1 кг корму, % | Вартість 1 кг корму, у. о. | |
| білку | клітковини | ||
| Зерно | 10 | 2 | 0,40 |
| Соєві боби | 50 | 8 | 0,90 |
Готова кормова суміш має містити не менше як 20 % білка і не більш як 5 % клітковини. Визначити масу кожного з двох видів кормів, що утворюють кормову суміш мінімальної вартості, водночас задовольняючи вимоги до загальної маси кормової суміші та її поживності. Для цього слід побудувати економіко-математичну модель поставленої задачі.
Побудова економіко-математичної моделі. Нехай х1 — маса зерна, а х2 — соєвих бобів (в кг) у готовій кормовій суміші.
Загальна кількість суміші х1 + х2 має становити понад 500 кг, тобто
х1 + х2 ≥ 500.
Розглянемо обмеження щодо поживності кормової суміші.
Суміш має містити не менш як 20 % білка:
10х1 + 50х2 ≥ 20 (х1 + х2),
а також не більше як 5 % клітковини:
2х1 + 8х2 ≤ 5 (х1 + х2).
Загалом математична модель задачі оптимізації кормового раціону має такий вигляд:
min Z = 0,40х1 + 0,90х2 (2.26)
за умов:

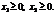 (2.30)
(2.30)
Розв’язання. Графічну інтерпретацію задачі подано на рисунку:

Множина допустимих її розв’язків необмежена. Для вектора 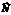 = (0,4; 0,9) можна змінити масштаб, наприклад,
= (0,4; 0,9) можна змінити масштаб, наприклад, 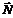 = (200; 450). Найменшого значення цільова функція Z досягає в точці А, що лежить на перетині граничних прямих, які відповідають обмеженням (2.27) та (2.28). Визначимо її координати:
= (200; 450). Найменшого значення цільова функція Z досягає в точці А, що лежить на перетині граничних прямих, які відповідають обмеженням (2.27) та (2.28). Визначимо її координати:

Отже, Х* = (375; 125); min Z = 0,4 · 375 + 0,9 · 125 = 262,5.
Згідно з відшуканим оптимальним планом задачі для того, щоб отримати 500 кг кормової суміші мінімальної вартості (262,50 у. о.), потрібно взяти 375 кг зерна та 125 кг соєвих бобів. За такого співвідношення компонентів кормової суміші вимоги до її поживності виконуватимуться:
0,10 · 375 + 0,50 · 125 = 100 кг білка, що становить рівно 20 % загальної маси суміші;
0,02 · 375 + 0,08 · 125 = 17,5 кг клітковини в кормовій суміші, що становить 3,5% її маси і не перевищує 5%.
2. На підприємстві встановлено нове обладнання. Залежність продуктивності цього обладнання від часу користування ним підприємством, а також залежність витрат на його утримання та ремонт при різному часі його використання наведені в таблиці.
| Показник | Час, протягом якого використовується обладнання | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | |
| Річний випуск продукції у вартісному вираженні (тис. грн) | 80 | 75 | 65 | 60 | 60 | 55 |
| Щорічні витрати, пов’язані з утриманням та ремонтом обладнання (тис. грн) | 20 | 25 | 30 | 35 | 45 | 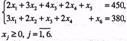 55 55
|
Знаючи, що витрати, які пов’язані з купівлею та установкою нового обладнання, ідентичного з встановленим, складають 40 тис. грн., а обладнання, що замінюється, списується, скласти такий план заміни обладнання протягом 5 років, при якому загальний прибуток за даний період часу максимальний.
!!!!!!!!!!!!!!!!!!Білет №25!!!!!!!!!!!!!!!!!
1. Продукція чотирьох видів А, В, С і D проходить послідовну обробку на двох верстатах. Тривалість обробки одиниці продукції кожного виду наведена в табл. 1.
Таблиця 1 – Тривалість обробки продукції на верстатах, год.
| Верстат | Тривалість обробки одиниці продукції | |||
| А | В | С | D | |
| 1 | 2 | 3 | 4 | 2 |
| 2 | 3 | 2 | 1 | 2 |
Витрати на виробництво одиниці продукції кожного виду визначають як величини, прямо пропорційні до часу використання верстатів (у машино-годинах). Вартість однієї машино-години становить 10 грн для верстата 1 і 15 грн – для верстата 2. Тривалість використання верстатів обмежена: для верстата 1 вона становить 450 машино-годин, а для верстата 2 – 380 машино-годин.
Ціна одиниці продукції видів А, В, С і D дорівнює відповідно 73, 70, 55 та 45 грн.
Визначити оптимальний план виробництва продукції всіх чотирьох видів, який максимізує загальний прибуток.
Розв’язати задачу лінійного програмування симплексним методом.
Дата добавления: 2018-04-05; просмотров: 360; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 х1
х1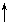
 х3
х3