Тема 5. Задачі в цілих числах

ШКІЛЬНИЙ КУРС МАТЕМАТИКИ.

ЗАДАЧІ ПІДВИЩЕНОЇ СКЛАДНОСТІ

Завдання до практичних занять

МОДУЛЬ А

(рік навчання 5, семестр 2)

Тема 1. Раціональний дріб, його основні властивості. Умовні тотожності. Похідні пропорції.

[2]: 66 – 68

66.Розв’язати рівняння

67.Розв’язати рівняння

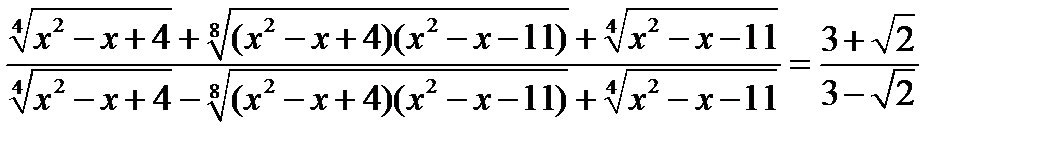
68.Розв’язати рівняння

[4]: 249, 250, 253, 255, 256, 258, 260

249. (5-6)Скоротити дріб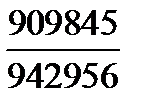

250. (5-6)Скоротити дріб

253. (6-10) Довести, що числа і взаємно прості для будь – якого натурального n.

255. ( 6-8)Знайти НСД двох чисел

і 1 111 111

256. (7- 8) Від прямокутника площею см² відрізають кілька квадратів см² доти, поки не залишиться прямокутник, довжина однієї із сторін якого менша за 62. Від отриманого прямокутника відрізають кілька квадратів із сторонами, довжина яких дорівнює меншій стороні прямокутника, і роблять так доти, поки не залишиться прямокутник, одна із сторін якого менша від сторони квадратів, що відрізаються. Так роблять, доки це можливо. Чому дорівнює сторона останнього відрізаного квадрата?

258. (8-10)m і n – два взаємно простих числа, і обидва діляться на деяке число p . Довести, що тоді для будь – якого натурального k 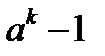ділиться на p.

260.Довести, що коли і - два числа Фібоначчі, то їхній НСД дорівнює , де (n,m) – найбільший спільний дільник n і m, тобто

Тема 2. Теорема Безу та її застосування.

[2]: 1, 4, 8 –10, 13 – 16

1. Знайти остачу від ділення

4. При якому значенні а многочлен при діленні на дає остачу, яка дорівнює 4?

8. При яких значеннях a і b многочлен ділиться на ?

9. Розкласти на множники

10. Розкласти на множники

13. Розв’язати рівняння

14. Розв’язати рівняння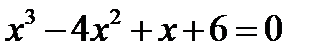

15. Розв’язати рівняння

16. Розв’язати рівняння

[1]: 23 – 28

Розкласти на множники:

23.

24.

25.

26.

27.

28.

Тема 3. Прогресії та послідовності. Обчислення сум.

[4]: 210, 112, 215 – 218, 221, 222 – 225

210.(8-9) Довести, що арифметична прогресія   складається з попарно взаємно простих чисел.

212. (6-9) Знайти арифметичну прогресію, що складається з трьох простих чисел p, p+10, p+20. Довести, що не існує арифметичної прогресії з різницею 10, що складається з взаємно простих чисел, причому має більше трьох чисел.

215. (8) Числа утворюють арифметичну прогресію. Довести, що

216. (8-9 )Числа x, y і z утворюють арифметичну прогресію. Довести, що коли x, y, z – цілі розв’язки рівняння то x кратне трьом, y – чотирьом, а z – п’яти.

217.(8-9) Числа x, y, z і u утворюють арифметичну прогресію і є цілими розв’язками рівняння Довести, що x кратне трьом, y – чотирьом, z – п’яти, u - шести.

218.(8-10)Знайти корені рівняння якщо відомо, що вони утворюють арифметичну прогресію.

221.  (8-10)Розв’язати систему рівнянь

де утворюють арифметичну прогресію і відомо, що x, y, z, які є розв’язком цієї системи рівнянь, також утворюють арифметичну прогресію.

222.(8-9)Всі члени зростаючих арифметичної і геометричної прогресій додатні, перші і треті однакові, другі відрізняються на 2, а четверті на 14. Знайти ці прогресії.

223. (8-9) У арифметичної і геометричної прогресій перші члени дорівнюють одиниці, треті однакові, а сума четвертих дорівнює нулеві. Знайти ці прогресії .

224. (8-9)Навести приклади арифметичної і геометричної прогресій, у яких однакові перший і другий члени. Встановити залежність, що зв’язує ці дві прогресії.

225. (8-10)Що можна сказати про арифметичну і геометричну прогресії, у яких однакові перший, m-й і (2m-1)-й члени?

Тема 4. Тотожні перетворення ірраціональних виразів.

[2]: 1 – 3, 8 – 12

Спростити вирази:

1.

2.

3.

8.

9.

10.

11.

12.

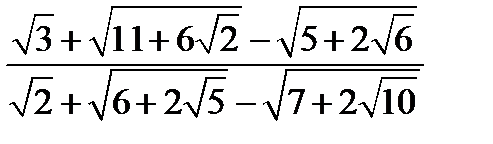
[1]: 57 – 62, 81 -83, 87 – 93

Виконати дії (спростити):

57.

58.

59.

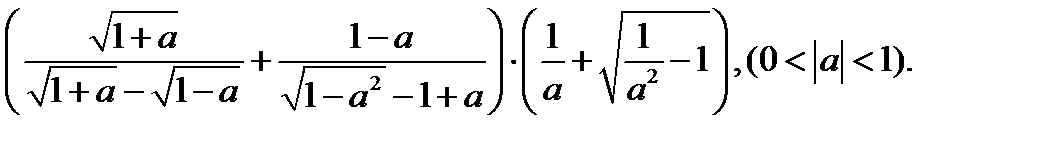
60.

61.

62.

Довести тотожності:

81.

82.

83.   при

Обчислити:

87.

88.

Знищити ірраціональність у знаменнику дробів:

89.

90.

91.

92.

93.

Тема 5. Задачі в цілих числах.

[20]: 1, 2, 4, 5(а,б), 6(а), 8(а,б), 9(в,г), 11

1.Довести, що:

а) якщо p – просте число і p>3, то p² -1 ділиться на 24;

б) якщо ділиться на 6, то   ділиться на 6 (a,b,c – цілі числа);

в) якщо ділиться на 7, то ділиться і на 49 (a,b – цілі числа );

г)число ні при якому цілому n не ділиться на 169.

2. При яких цілих а обидва корені рівняння є цілими числами?

4. Знайти число дільників числа n, якщо :

а)n=1024;

б)n=210;

в)    ( - натуральні, - різні прості числа);

г) ( - означає перетворення ).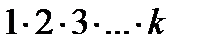

5. а)Які остачі можуть давати точні квадрати при діленні на 3, або 4?

б) Чи може дискримінант квадратного рівняння з цілими коефіцієнтами дорівнювати 23?

6. а) В десятковому записі числа 300 одиниць і декілька нулів (інших цифр немає). Чи може це число бути точним квадратом?

Розв’язати в цілих числах рівняння:

8. а)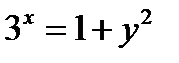

б)

9. в)

г)

11. Дано Знайти кількість цифр і першу цифру числа .

Тема 6. Основні методи та штучні прийоми розв’язування алгебраїчних рівнянь та їх систем.

[2]: 1 – 12, 31 – 36, 42 – 47, 52 – 57, 80 – 83, 1;3 (ст. 82), 5 – 10,17 – 20, 24, 26

Розв’язати рівняння:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

31.

32.

33.

34.

35.

36.

42.

43.

44.

45.

46.

47.

52.

53.

54.

55.

56.

57.

80.

81.

82.

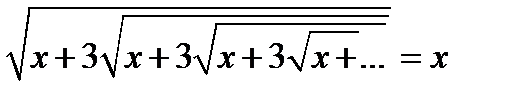
83.

1;3 (ст. 82), 5 – 10,17 – 20, 24, 26

Розв’язати систему рівнянь

1.

3.

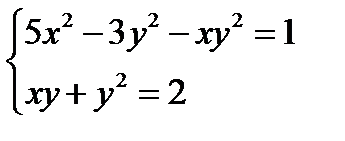
5.

6.

7.

8.

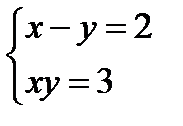
9.

10.

17.

18.

19.

20.

24.

26.

Тема 7. Метод інтервалів. Розв’язування ірраціональних нерівностей. Комбіновані рівняння і нерівності. Графічний метод.

[6]: 1.481 – 1.495

Розв’язати нерівності

1.481.

1.482.

1.483.

1.484.

1.485.

1.486.

1.487.

1.488.

1.489.

1.490.

1.491.

1.492.

1.493.

1.494.

1.495.



[2]: 19 – 25, 30 – 32

Розв’язати нерівності

19.

20.

21.

22.

23.

24.

25.

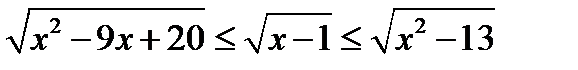
Тема 8. Розв’язування рівнянь і нерівностей з параметрами. Властивості коренів квадратного рівняння.

[2]: 8, 13, 15, 20 (ст.96), 4 (ст. 101), 6 – 10 (ст.104), 1 – 7 (ст.108), 1 (ст.116), 1, 4 (ст.124), 1,2 (ст.130)

8, 13, 15, 20 (ст.96),

Розв’язати рівняння:

8.

13.

15. Визначити, при яких значеннях t рівняння мають додатні розв’язки:

а)

б)

20. Визначити, при яких значеннях параметра а рівняння матиме корінь більший, ніж – 1

4 (ст. 101)

4. Дослідити і розв’язати системи рівнянь

а)

б)

в)

г)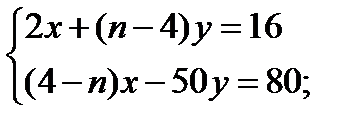

6 – 10 (ст.104)

Розв’язати рівняння:

6.

7.

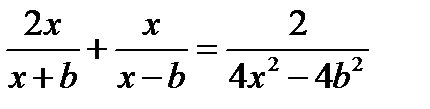
8.

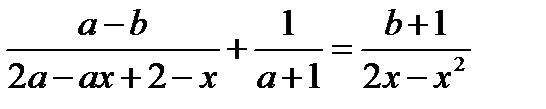
9.

10.

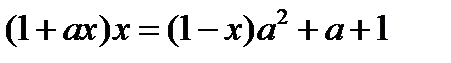
1 – 7 (ст.108)

1. Знайти b, якщо корені рівняння дійсні та

2. Знайти значення а, при яких корені рівняння рівні між собою.

3. При яких значеннях m рівняння не має дійсних коренів?

4. Знайти цілі значення k, при яких рівняння не має дійсних коренів

5. Знайти найменше ціле число k, при якому рівняння має два різні дійсних кореня.

6. При яких значеннях а сума коренів рівняння дорівнює нулеві?

7. При яких значеннях а відношення коренів рівняння      дорівнює 2?

1 (ст.116)

1.Для яких дійсних значень а рівняння має один корінь, який більший за 3, а другий – менший за 2?

1, 4 (ст.124)

Розв’язати нерівності

1.

4.

1, 2 (ст.130)

Знайти всі значення параметра а, при яких корені рівняння дійсні числа, і визначити їх знаки

1.

2.

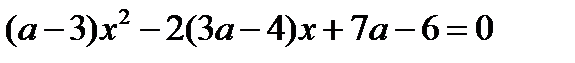
Тема 9. Доведення нерівностей.

[6]: 1.204 (а), 1.211, 1.223, 1.227

1.204. (а) Довести нерівність ,де   і

1.211. Довести нерівність при

1.223. Довести, що для додатних a і b виконується нерівність

1.227. Довести нерівності

а)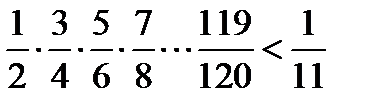

б)

в)

г)

Тема 10. Функції “антьє” і “мантиси” в рівняннях і нерівностях.

[4]: 124, 125, 128, 129, 131, 134, 138, 143

Знайти множину цілих невід’ємних розв’язків і визначити кількість таких розв’язків:

124. (7-10)

125. (8) Скільки існує натуральних чисел, третій степінь яких не перевищує 1 000 001 ?

128.(5-6)

129. (8-10) (Операції ділення на 2 і відшукання цілої частини повторені n раз)

131. (8-10)

134.(8-10)

138. (8-10)

143. (8) Визначити х , якщо саме х, його ціла частина [x] і його дробова частина {x} утворюють геометричну прогресію.

Тема 11. Функціональні рівняння.

[5]: 1 (а – д), 2, 3 (ст.11), 1, 2 (ст. 7), 1 (ст.20)

1 (а – д), 2, 3 (ст.11),

1. Розв’язати функціональні рівняння:

а)

б)

в)

г)

д)

2.Знайтивсі функції , які задовольняють функціональне рівняння , де а – деяка натуральна стала (параметр).

3. Знайти всі розв’язки функціонального рівняння де - дійсна функція, причому і для всіх виконується умова

1, 2 (ст. 7)

1.Знайти неперервні функції , визначені на множині дійсних чисел, які задовольняють функціональні рівняння:

а)

б)

в)

2.   Знайти неперервні функції , визначені на множині додатних дійсних чисел, які задовольняють функціональні рівняння:

а)

б)

в)

г) де а – деяка дійсна стала (параметр).

1 (ст.20)

1.В класі диференційованих функцій розв’язати рівняння:

а)

б)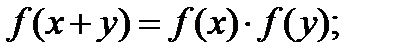

в)

г)

Тема. 12. Принцип Діріхле.

[3]: 1 – 8 (ст.54)

1. На ділянці лісу, яка має форму квадрата площею 1 км², на кожному прямолінійному відрізку довжиною 100 м росте принаймні одне дерево, радіус якого не менший 60 см. Чи можна стверджувати, що на ділянці не менше 7430 таких дерев?

2. Доведіть, що серед 82 кубиків, кожний з яких зафарбовано в певний колір, завжди можна вибрати 10 кубиків так, щоб вони всі були зафарбовані в різні кольори або в один колір.

3. Площину довільно розфарбовано у два кольори. Довести, що знайдуться дві точки одного кольору на відстані 1 м одна від одної.

4. Чи знайдеться число вигляду 111…100…0(починається з 1, а закінчується нулями), яке ділиться на 1992?

5. Доведіть,що серед будь – яких 1992 натуральних чисел можна вибрати кілька чисел таким чином, щоб їхня сума ділилась на 1992.

6. У клітинках шахової дошки   записано цілі числа так, що різниця між будь – якими двома числами сусідніх клітинок(клітинки, які мають спільну сторону) не більша 20. Довести, що на дошці знайдеться принаймні три клітинки, в яких записано однакові числа.

7. Усередині квадрата, сторона якого дорівнює 1, розміщено 101 точку так, що жодні три не лежать на одній прямій. Довести, що серед цих точок знайдеться три таких, що площа трикутника, вершинами якого є ці точки, не перевищую 0,01.

8. У прямокутнику із сторонами довжиною 1 та 2 дано точок. Довести, що існує круг радіуса , який містить не менше трьох з даних точок.

Тема 13. Принцип пошуку інваріанта. Ігри, стратегії, турніри. Маршрути, розфарбовування в задачах.

[3]: 11 – 17 (ст.61)

11. У кожній вершині куба записано число. За один крок до двох чисел, розміщених на одному (будь – якому) ребрі, додається по одиниці. Чи можна за кілька таких кроків зробити всі вісім чисел різними між собою, якщо спочатку числа розміщено так, як показано на рис 25?

12. Є дві купи камінців. Двоє гравців по черзі роблять такі ходи: забирають одну з куп, а другу ділять на дві частини. Якщо гравець при своєму ході не може розділити купу на дві частини(оскільки в ній залишається один камінець), то він програє. Хто виграє при правильній грі? Якою має бути стратегія успіху?

13. Двоє по черзі зривають пелюстки ромашки, причому за один раз можна зірвати або одну пелюстку, або дві сусідніх пелюстки. Виграє той, хто зробить останній хід. Хто ж з гравців виявиться переможцем?

14. Чи можна шахову дошку розміром обійти конем так, щоб на кожному полі побувати рівно один раз і повернутися на початкове поле?

15. Куб розбито на 27 однакових кубиків. Жук знаходиться в центральному кубику. З кожного кубика він може перейти в один із шести сусідніх кубиків(що мають з ним спільну грань). Чи може жук обійти всі кубики, побувавши в кожному з них рівно по одному разу?

16. Чи можна скласти куб розміром 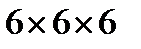з 27 «цеглин» розміром ?

17. Чи можна з 1991 квадратної плитки утворити замкнений ланцюг?

8 -16 (ст.75)

8. Дві вершини трикутника закріплено в точках А і В, а третя вершина С переміщується в площині так, що різниця від неї до точок А і В є сталою величиною(СА - СВ= const). Довести, що центри кіл, вписаних у трикутник АВС, лежить на одній прямій.

9. У вершинах кількох правильних трикутників довільно записано числа1;2;3. Трикутники склали таким чином, що їхні вершини збіглись. Чи можуть суми чисел, записаних у кожній вершині, дорівнювати 1987?

10. На дошці написано три цілих числа. Одне з них витерли і замість нього написали суму двох чисел, що залишились, зменшену на одиницю. Цю операцію повторили кілька годин, і в результаті дістали числа 17; 1967; 1983. Чи правильно, що на дошці спочатку були написані числа а) 2;2;2; б) 3; 3; 3?

11. З шахової дошки розміром вирізано одну кутову клітинку. Чи можна частину дошки, що залишилась, покрити кісточками доміно так, щоб рівно половина з них була розміщена на горизонталях дошки?

12. З шахової дошки розміром вилучили одну кутову клітинку. Чи можна її покрити прямокутниками, складеними з трьох клітинок?

13. Чи можна шахову дошку покрити чотириклітинковими фігурами, які показано на рис. 35?

14. Чи можна шахову дошку розміром покрити прямокутниками, складеними з чотирьох клітинок ?

15. Дано кілька( не менше двох) чисел, що не дорівнюють нулю. Дозволяється стерти будь – які два числа А, В і записати замість них числа . Доведіть, що після кількох таких операцій неможливо знову дістати початковий набір чисел.

16. Кожний член парламенту має не більш трьох опонентів. Доведіть, що парламент можна поділити на дві палати так, щоб кожний парламентарій в одній з ним палаті мав не більше одного опонента.

Тема 14. Комбінаторні сполуки та їх види. Біном Ньютона.

[6]: 1.880 – 1.883

Довести тотожності:

1.880.   ,де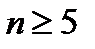

1.881.

1.882.

Розв’язати рівняння:

1.883.

[1]: 1534 – 1540, 1556 – 1558, 1581

Розв’язати рівняння:

1534.

1535.

1536.

1537.

1538.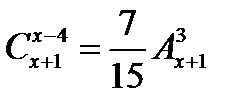

1539.

1540.

Довести, що:

1556.

1557.

1558.

1581. При якому значенні х коефіцієнт четвертого члена розкладу бінома дорівнює показнику бінома?

Тема 15. Доведення тригонометричних тотожностей і нерівностей.

[6]: 2.26 – 2.30, 2.38, 2.49, 2.58

Довести тотожності

2.26.

2.27.

2.28.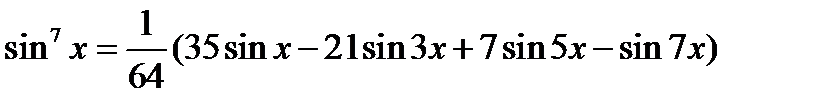

2.29.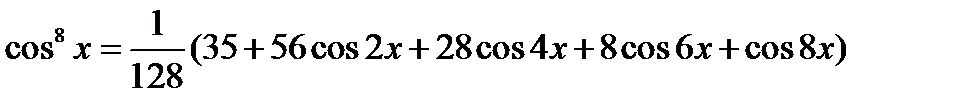

2.30.

Довести рівності:

2.38.

Довести умовні тотожності:

2.49.   , якщо

2.58. Довести нерівності:

а)

б)

в)

Тема 16. Розв’язування нестандартних тригонометричних рівнянь, нерівностей та їх систем. Тригонометричні рівняння з параметрами.

[6]: 2.114, 2.131, 2.156, 2.166 – 2.168, 2.176, 2.177

2.114. Розв’язати рівняння:

а)

б)

в)

г)

д)

е)

є)

2.131.

2.156. Розв’язати нерівності:

а)

б)

в)

г)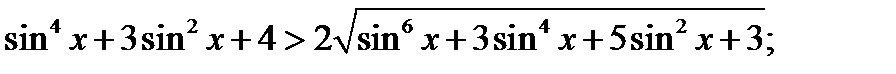

д)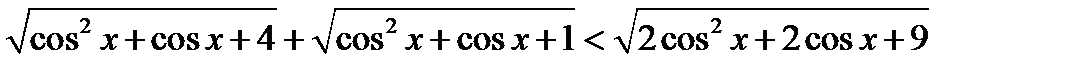

е)

Розв’язати рівняння:

2.166.

2.167.

2.168.

Розв’язати нерівності

2.176.

2.177.

Тема 17. Доведення тотожностей і нерівностей, які містять обернені тригонометричні функції.

[6]: 2.266, 2.275, 2.276, 2.279, 2.282, 2.273

Довести, що:

2.266.

2.273.

2.275. , при

2.276.

Довести нерівності:

2.279.

2.282.

Тема 18. Розв’язування рівнянь і нерівностей, які містять обернені тригонометричні функції.

[6]: 2.308 – 2.310, 2.314, 2.327, 2. 328, 2.331 – 2.334

Розв’язати рівняння:

2.308.

2.309.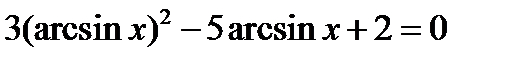

2.310.

2.314.

Розв’язати нерівності:

2.327.

2.328.

2.331.

2.332.

2.333.

2.334.

Тема 19. Розв’язування нестандартних показникових рівнянь, нерівностей та їх систем. Показникові та логарифмічні рівняння з параметрами. Розв’язування показниково-степеневих рівнянь.

[2]: 9, 11, 17, 22, 31, 37, 60 (ст.164)

Розв’язати рівняння:

9.

11.

17.

22.

31.

37.

60.

7 (ст.171)

Розв’язати систему рівнянь:

7.

23, 24 (ст.177)

Розв’язати нерівності:

23.

24.

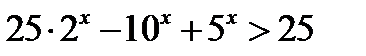
27 (ст.180)

Розв’язати нерівності:

27.

Тема 20. Контрольна робота

Тема 21. Основні властивості функцій. Застосування похідної у фізиці та геометрії. Застосування похідної до розв’язування рівнянь та нерівностей.

[20]: 56 (а), 57, 58, 67, 211, 224, 229, 230, 233 (а), 234 (а,б), 240 – 243

56. а)Довести, що для будь – якої функції з симетричною відносно точки О областю визначення функція парна, а функція непарна.

57. Функція і періодичні з загальним періодом . Довести, що функція і є періодичними з періодом .

58. Довести, що сума двох неперервних періодичних функцій, визначених на всій числовій прямій і які не мають спільних періодів, не є періодичною.

67. При яких n функція може мати рівно n точок екстремуму, якщо відомо, що : а) парна; б) непарна; в) періодична функція?

211.Довести,що функція не має похідної в точці О.

224.Довести, що будь – яке кубічне рівняння має хоча б один дійсний корінь.

229. Три пункти А, В, С не лежать на одній прямій, причому . Одночасно із точки А виїжджає автомобіль, а із точки В – поїзд. Автомобіль рухається в напрямку до В з швидкістю , поїзд – до С з швидкістю . В який момент часу (від початку руху) відстань між поїздом і автомобілем буде найменшою, якщо АВ=200 км?

230.На сторінці текст повинен займати 384 см².Верхні і нижні поля повинні бути по 3 см, праве і ліве – по 2 см. Якщо взяти до уваги тільки економію паперу, то яким повинні бути найбільш вигідні розміри сторінки?

233. Що більше: а) 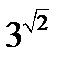або

234. Довести, що якщ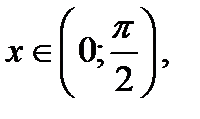о то:

а)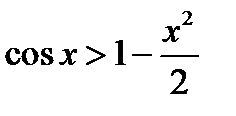

б)

240. Колесо радіуса R котиться по прямій. Кут φ повороту колеса за t секунд визначається рівнянням . Знайти швидкість і прискорення руху центра колеса.

241. Лампа підвішена на висоті 12 мнад прямою горизонтальною доріжкою по якій іде людина зростом 1,8 м. З якою швидкістю його тінь подовжується, якщо він віддаляється від лампи зі швидкістю ?

242.Під яким кутом перетинається графіки функцій і ?

243.Запишіть рівняння дотичної до графіка функції , яка проходить через точку М, якщо:

а)

б)

в)

г)

Тема 22. Первісна та інтеграл.

[20]: 251, 255 – 258, 266, 274 – 278

251.Знайти всі первісні для функцій:

а)

б)

в)

г)

255. Довести, що будь – яка первісна непарної неперервної функції, визначена на 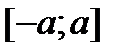, є парною функцією.

256.Довести, що парна неперервна функція, визначена на 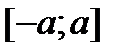має принаймні одну непарну первісну.

257.Два тіла почали рухатися по прямій одночасно з однієї точки. Швидкість першого , другого . В який момент і на якій відстані від початкової точки відбудеться їх зустріч? (Швидкість вимірюється в метрах за секунду).

258. Нехай при рухові по прямій тіло масою m в точці з координатою х має потенціальну енергію . Довести, що:

а)координата тіла при рухові по прямій задовольняє диференціальне рівняння

б)потенціальна енергія матеріальної точки масою m, яка здійснює гармонічне коливання , рівна , де 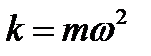(положення )

266. Матеріальна точка рухається по прямій. Довести, що:

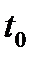а) ,якщо відома її швидкість в будь – який момент і координата точки в початковий момент рівна

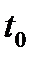б) , якщо відомо її прискорення в будь – який момент і швидкість в початковий момент рівна

274. Обчислити площу фігури, яка складається з точок, що лежать всередині еліпса. (Еліпсом називається фігура, координати точок якої задовольняють рівняння )

275. При яких значеннях параметра а, b, c визначений інтеграл:

а)

б)

в)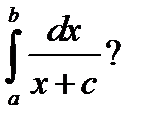

276. Знайти площу фігури обмежену лініями:

а) і

б)

277. Площа фігури обмежена лініями   рівна . Знайти а.

278. Довести, що площа параболічного сегмента, який знаходиться між параболою і довільною прямою, паралельною осі абсцис, рівна площі прямокутника з вершинами в точках перетину прямої з параболою і основами перпендикулярів до осі абсцис, опущених із точок перетину.

Тема 23. Планіметричні задачі на обчислення.

[1]: 1620 – 1625, 1647, 1727, 1729, 1800, 1797, 1947, 1951

1620. У прямокутному трикутнику бісектриса прямого кута поділяє гіпотенузу у відношенні 7:9. В якому відношенні поділяє гіпотенузу висота?

1621. Катети прямокутного трикутника дорівнюють 2 і 6. Знайти довжину бісектриси прямого кута.

1622. У прямокутному трикутнику бісектриса гострого кута поділяє катет на відрізки m і n. Знайти сторони трикутника.

1623. Основа висоти прямокутного трикутника, проведеної на гіпотенузу, віддаленої від катетів на 3 см і 4 см. Знайти довжину гіпотенузи.

1624. Довести, що радіус кола, вписаного в прямокутний трикутник, дорівнює піврізниці між сумою катетів і гіпотенузою.

1625. Знайти катети прямокутного трикутника, якщо їх відношення дорівнює 20: 21, а різниця між радіусами описаного та вписаного кіл 17 см.

1647. Сторони трикутника дорівнюють a, b, c. Знайти довжини його медіан.

1727. Знайти кути рівнобедреного трикутника, якщо центри вписаного і описаного навколо нього кіл симетричні відносно основи.

1729. Навколо кола радіуса R описано рівнобічну трапецію, менша сторона якої дорівнює 2а. Знайти діагональ трапеції.

1797. Сторона рівностороннього трикутника, вписаного в коло, дорівнює а. Визначити площу меншого сегмента, що відтинається стороною трикутника.

1800. У прямокутний трикутник вписано квадрат так, що одна з його сторін лежить на гіпотенузі. Відрізки гіпотенузи від вершин трикутника до вершин квадрата дорівнює m і n. Знайти площу квадрата.

1947. Знайти кути рівнобедреного трикутника, якщо його ортоцентр лежить на колі, вписаному в трикутник.

1951. Знайти кут паралелограма, якщо його висоти дорівнюють h₁ і h₂ , а периметр - 2p.

Тема 24. Застосування векторного та координатного методів до розв’язування задач планіметрії.

[27]: 17.043, 17.049, 17.063, 17.076, 17.116, 17.124

17.043. В правильній чотирикутній піраміді SABCD довжина кожного ребра рівна а. Точка і . Знайти кут між векторами   і .

17.049. Медіани бічних сторін рівнобедреного трикутника перетинаються під кутом . Знайти кут при вершині трикутника.

17.063.В трикутнику АВС точка N лежить на стороні АВ і AN=3NB; медіана АМ перетинається з CN в точці О. Знайти АВ, якщо АМ=СN=7 см і

17.076.В трикутнику АВС дано: АВ=ВС; D – середина сторони АС; DK перпендикулярна ВС; точка М – середина відрізка DK. Довести, що прямі АК і ВМ перпендикулярні.

17.116.Навколо квадрата описано коло. Довести, що сума квадратів відстаней точок кола до вершин квадрата не залежить від вибору цих точок. Знайти цю суму.

17.124.В коло вписано трикутник АВС. Пряма, яка містить медіану СС₁ трикутника, перетинає коло вдруге в точці D. Довести, що

Тема 25. Планіметричні задачі на доведення.

[1]: 1616 – 1619,1718 – 1721, 1931, 1946, 1732 – 1735, 1767, 1769, 1787

1616. Довести, що трикутник, в якому медіана дорівнює половині сторони, на яку вона проведена, є прямокутником.

1617. Довести, що в прямокутному трикутнику медіана, проведена на гіпотенузу , дорівнює її половині.

1618. Довести, що в прямокутному трикутнику медіана і висота, проведені на гіпотенузу, утворюють кут, який дорівнює різниці гострих кутів трикутника.

1619. Довести, що квадрати катетів прямокутного трикутника відносяться як їх проекції на гіпотенузу.

1718. Довести, що для двох концентричних кіл сума квадратів відстаней довільної точки одного з них до кінців довільного діаметра другого є величина стала.

1719. Через одну з точок перетину двох кіл проведено діаметри кожного кола. Довести, що пряма, яка сполучає кінці цих діаметрів, проходить через другу точку перетину кіл.

1720. Довести, що коли через точку дотику двох кіл проведено дві січні і кінці їх сполучено хордами, то ці хорди паралельні.

1721. З точки Р до кола О проведено дві дотичні РА і РВ і через точку В проведено діаметр ВС. Довести, що прямі СА і ОР паралельні.

1732. Всередині рівностороннього трикутника взято довільну точку, з якої опущено перпендикуляри на сторони трикутника. Довести, що сума цих трьох перпендикулярів дорівнює висоті трикутника.

1733. Сторони трикутника дорівнюють 4 см, 13 см і 15 см. Всередині нього взято точку, віддалену на 5 см від першої сторони і на 1 см – від другої. Знайти відстань цієї точки від третьої сторони.

1734. У коло вписано правильний трикутник. Через середини двох дуг, що стягуються сторонами трикутника, проведено хорду. Довести, що сторони трикутника поділяють хорду на три рівні частини.

1735. На колі, описаному навколо рівностороннього трикутника АВС, взято довільну точку М. Довести, що найбільший з відрізків МА, ВМ, СМ дорівнює сумі двох інших.

1767. Довести, що медіани трикутника поділяють його на шість рівновеликих частин.

1769. Довести, що площа трикутника, сторони якого є медіанами другого трикутника, дорівнює   площі цього трикутника.

1787. У паралелограмі середину кожної сторони сполучено з кінцем наступної сторони. Довести, що площа внутрішнього паралелограма дорівнює площі заданого.

1931. Довести, що коли медіана і висота, проведені з однієї вершини кута трикутника, поділяють цей кут на три рівні частини, то такий трикутник прямокутний.

1946. Довести, що пряма, симетрична медіані відносно бісектриси внутрішнього кута трикутника, поділяє протилежну сторону на частини, пропорційні квадратам прилеглих сторін.

Тема 26. Геометричні нерівності та задачі на екстремум.

[7]: 9.3, 9.17, 9.24, 9.34, 9.43, 9. 52, 9.74, 11.5, 11.21, 11.33, 11.36

9.3. Дано n точок і коло радіуса 1. Доведіть, що на колі можна вибрати точку М так, що .

9.17. Дано замкнену ламану, причому будь – яка інша замкнута ламана з тими ж вершинами має більшу довжину. Довести, що ця ламана не само перетинаюча.

9.24. Довести, що якщо довжини сторін трикутника пов’язані нерівністю , то с – довжина найменшої сторони.

9.34. В коло радіуса R вписаний многокутник площею S, який містить центр кола і на його сторонах вибрано по точці. Довести, що периметр випуклого многокутника з вершинами у вибраних точках не менше .

9.43. Квадрат розрізаний на прямокутники. Довести, що сума площ кругів, описаних навколо всих цих прямокутників, не менше площі круга, описаного навколо вихідного квадрата.

9.52. Довести, що площа паралелограма, який лежить всередині трикутника не перевищує половини площі трикутника.

9.74. Довести, що якщо кути випуклого п’ятикутника утворюють арифметичну прогресію, то кожний з них більший за .

11.5. Серед всих трикутників, вписаних в дане коло, знайти той у якого сума квадратів довжин сторін максимальна.

11.21. Дано трикутник АВС. Знайти всередині нього точку О для якої сума довжин відрізків ОА, ОВ, ОС мінімальна.(Зверніть увагу на випадок коли один з кутів трикутника більший за )

11.33. На основі АD трапеції ABCD дано точку К. Знайти на основі ВС точку М для якої площа спільної частини трикутників AMD і BKC максимальна.

11.36. Серед всих многокутників, вписаних в дане коло, знайти той у якого сума квадратів довжин сторін максимальна.

Тема 27. Стереометричні задачі на обчислення.

[1]: 1999, 2004, 2022, 2062, 2111, 2150

1999. Основою прямого паралелепіпеда є ромб, гострий кут якого дорівнює а. Під яким кутом до основи треба провести січну площину, щоб в перерізі дістати квадрат, вершини якого лежать на бічних ребрах.

2004. Діагональ прямокутного паралелепіпеда утворює з більшою гранню кут α. Через менші сторони основ проведено січну площину. Знайти об’єм паралелепіпеда, якщо периметр перерізу дорівнює m, площина цього перерізу утворює з площиною кут β.

2022. В основі прямокутної призми лежить рівносторонній трикутник. Через одну з його сторін під кутом α до основи призми проведено площину, яка відтинає від призми трикутну піраміду, що має об’єм V. Знайти площу перерізу.

2062. Об’єм правильної трикутної піраміди дорівнює V, а двогранний кут при ребрі основи α. Знайти повну поверхню піраміди.

2111. Бічне ребро правильної зрізаної чотирикутної піраміди дорівнює l і утворює з площиною основи кут β. Діагональ піраміди перпендикулярна до бічного ребра. Знайти об’єм піраміди.

2150. Знайти довжину радіуса кулі, якщо при збільшенні його довжини на q см, об’єм сферичного сектора, який дорівнює V см³ , збільшується на p см³.

Тема 28. Застосування векторного та координатного методів до розв’язування задач стереометрії.

[27]: 17.024, 17.030, 17.043, 17.047, 17.056, 17.060, 17.088, 17.095

17.024. Скласти рівняння сфери, яка проходить через точку А(1; -1; 4) і дотикається до координатних площин.

17.030. Довести, що сума квадратів довжин всіх ребер паралелепіпеда рівна сума квадратів довжин всіх його діагоналей.

17.043. В правильній чотирикутній піраміді SABCD довжина кожного ребра рівна а. Точка і . Знайти кут між векторами   і .

17.047.В прямокутному паралелепіпеді АВСDA₁ B₁ C₁ D₁ дано: АА₁=10, AD=6, AB=8. Знайти косинус кут між векторами і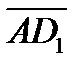

17.056. Знайти об’єм трикутної піраміди , побудованої на векторах і , якщо .

17.060.Дано координати вершин піраміди: . Знайти координати точки М, яка лежить на осі Oz s координат точки N, яка лежить в площині SBC, якщо відомо, що

17.088.Довести, що якщо сума квадратів протилежних ребер тетраедра рівні, то ці ребра попарно перпендикулярні.

17.095.Відомо довжини ребер тетраедра ABCD. Знайти косинус кута між протилежними ребрами AB і CD.

Тема 29. Комбінації геометричних тіл. Доведення тверджень стереометрії.

[1]: 2170, 2259, 2185, 2158

2158. Довести, що об’єм тіл, утворених обертанням довільного трикутника послідовно навколо кожної з його сторін, обернено пропорційні цим сторонам.

2170. Сегмент круга обертається навколо діаметра, що проходить поза сегментом через кінець хорди і утворює з його хордою, яка дорівнює а, кут α. Знайти об’єм утвореного тіла обертання.

2185. Довести, що в правильну піраміду можна вписати кулю.

2259. Довести, що площа бічної поверхні конуса, вписаного в кульовий сегмент, є середнє геометричне між площею основи та площею бічної поверхні сегмента.

Тема 30. Задачі на екстремум у просторі.

Дод.[4]: 70,82,86(а)

70. Довести, що сума довжин ребер многогранника більша за 3d , де d – відстань між найбільш віддаленими вершинами многогранника.

82. Із двох точок А і В, відстань між якими d км, одночасно на протязі однієї секунди спостерігають за літаком, який летить по прямій з постійною швидкістю. (рис. 5). Із точки А повідомили, що літак змістився за цю секунду на кут α, а із точки В – що літак змістився на кут β ( кути α і β гострі). Яку найменшу швидкість міг мати літак?

86. (а) Прожектор освітлює кут . Довести, що розміщення в чотирьох довільних точках площини прожектора можна направити так, щоб освітити всю площину.

Тема 31. Задачі на побудову циркулем і лінійкою

[1]: 1815 – 1830

1815. Побудувати квадрат за сумою сторони і діагоналі.

1816. Побудувати прямокутний трикутник за гіпотенузою та сумою катетів.

1817. Всередині трикутника побудувати таку точку, що прямі, які сполучають її з вершинами трикутника, поділяли цей трикутник на три рівновеликі частини.

1818. Побудувати трикутник за основою, кутом при вершині та сумою двох інших сторін.

1819. Побудувати трикутник за основою та медіанами, проведеними на бічні сторони.

1820. У коло вписати трикутник, якщо задано його основу та відношення бічних сторін.

1821. Побудувати трикутник за основою, прилеглим до неї кутом, який утворює медіана, проведена з вершин заданого кута, із стороною, на яку вона проведена.

1822. Побудувати трикутник за трьома медіанами.

1823. Побудувати чотирикутник ABCD за його сторонами, знаючи, що діагональ АС є бісектрисою кута А.

1824. Дано коло і на ньому точки А, В і С . У це коло вписати такий трикутник, щоб продовження його висот перетинали коло у заданих точках.

1825. Побудувати трикутник за кутом при вершині та висотою і медіаною, проведеними до основи.

1826. Побудувати прямокутний трикутник за гіпотенузою та різницею катетів.

1827. Побудувати коло, яке дотикається до заданої прямої і до заданого кола в заданій на ньому точці.

1828. Через задану точку основи трикутника провести пряму, що поділяє трикутник на рівновеликі частини.

1829. З точки поза колом провести січну так, щоб її зовнішня частина дорівнювала внутрішній.

1830. Побудувати прямокутний трикутник за гіпотенузою та бісектрисою прямого кута.

Тема 32. Геометричні місця точок у просторі.

[23]: 1 – 10 (ст. 85)

1. На поверхні куба знайти точки, кожна з яких рівновіддалена:

а) від двох його основ;

б) від двох його діагоналей;

в)від двох суміжних граней;

2. На поверхні куба знайти точки, які віддалені від вершини на відстань, яка дорівнює ребру(г. м. І).

3. На поверхні куба знайти точки, які віддалені від вершини А на відстань, яка дорівнює діагоналі його грані.

4. На поверхні циліндра знайти точки, які рівновіддалені від його основ (г. м. VI).

5.Знайти геометричне місце точок на поверхні циліндра, які рівновіддалені від двох точок, що лежать:

а)на одній і тій же твірній

б)на колі основи ( г. м. IV)

6.  На поверхні даної кілі знайти точки, кожна з яких рівновіддалена від двох діаметрально протилежних точок цієї кулі ( г. м. IV).

7.Знайти точки, які лежать на поверхні кулі і рівновіддалені від двох довільних точок цієї кулі ( г. м. IV).

8. Знайти точки, які знаходяться на поверхні кулі радіуса r і рівновіддалені від її центра, і від довільної точки на площині цієї кулі ( г. м. IV).

9.На поверхні циліндра радіуса r знайти точки, кожна з яких віддалена від центра основи на відстань, яка рівна 2r ( г. м. I).

10. На поверхні куба знайти точки, які віддалені від його центра на відстань, яка рівна половині діагоналі грані.

Тема 33. Побудова перерізів многогранників

Дод.[10]: задачі додатку

1.Методом слідів(мал. 111-140) і внутрішнього проектування (мал. 141-154) побудувати перерізи даних геометричних тіл.

2.Побудувати тіні непрозорих просторових фігур на горизонтальну площину при заданому освітленні L(l) (мал. 155-157).

Тема 34. Контрольна робота



Дата добавления: 2018-04-05; просмотров: 598; Мы поможем в написании вашей работы!
Поделиться с друзьями:

Мы поможем в написании ваших работ!