Задача №2 ЭТУ ЗАДАЧУ НУЖНО ЗАМЕНИТЬ, ОЧЕНЬ МНОГО СЧЕТА
1
Задача №1
Интегральная функция распределения F(x) непрерывной случайной величины задана следующим образом.
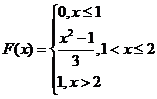
Найти плотность распределения этой случайной величины, вычислить числовые характеристики распределения и построить графики функции распределения и плотности распределения.
Задача №2
По данным выборочного обследования получено следующее распределение семей по среднедушевому доходу:
| Среднедушевой доход семьи в месяц (у.е.) | до 25 | 25-50 | 50-75 | 75-100 | 125-150 | 150-175 | 175 и выше |
| Количество обследованных семей | 46 | 236 | 250 | 176 | 102 | 78 | 12 |
Постройте гистограмму распределения частот. Найдите среднедушевой доход семьи в выборке, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Объясните полученные результаты.
Решение.
| Среднедушевой доход семьи в месяц (у.е.) | Количество обследованных семей | Середины интервалов | 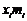
| 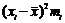
|
| 0-25 | 46 | 12,5 | 575 | 192024,8 |
| 25-50 | 236 | 37,5 | 8850 | 370272,7 |
| 50-75 | 250 | 62,5 | 15625 | 53363,03 |
| 75-100 | 176 | 87,5 | 15400 | 18999,57 |
| 125-150 | 102 | 137,5 | 14025 | 371989,1 |
| 150-175 | 78 | 162,5 | 12675 | 568733,3 |
| 175-200 | 12 | 187,5 | 2250 | 146231,4 |
| Сумма | 900 | - | 69400 | 1721614 |
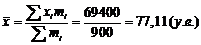
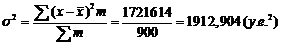
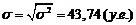
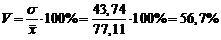
2
Задача №1
На столе стоят 3 телефона. Вероятности того, что зазвонит каждый из них, соответственно равны 0.5, 0.6, 0.8. Составьте закон распределения числа телефонов, зазвонивших в течение часа, и вычислите числовые характеристики этого распределения. Какова вероятность того, что зазвонит не более двух телефонов?
|
|
|
Решение
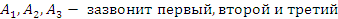
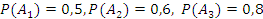
| X – число зазвонивших телефонов | 0 | 1 | 2 | 3 |
| P(X=m) | 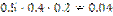
| 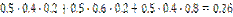
| 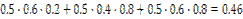
| 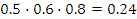
|
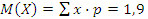
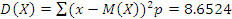
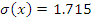
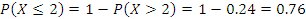
Задача №2
С целью изучения размеров дневной выручки в сфере мелкого частного бизнеса была произведена 10%-ная случайная бесповторная выборка из 1000 торговых киосков города. В результате были получены данные о средней дневной выручке, которая составила 500 у.е. В каких пределах с доверительной вероятностью 0,95 может находиться средняя дневная выручка всех торговых точек изучаемой совокупности, если среднее квадратическое отклонение составило 150 у.е.?
Решение.
N=1000, 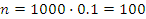 ,
, 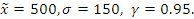
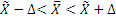
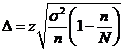
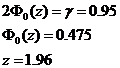
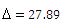
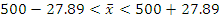
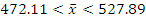
3
Задача №1
Интегральная функция распределения F(x) непрерывной случайной величины задана следующим образом.
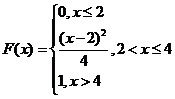
Найти плотность распределения этой случайной величины, вычислить числовые характеристики распределения и построить графики функции распределения и плотности распределения.
Задача №2
Для оценки состояния деловой активности промышленных предприятий различных форм собственности были проведены выборочные бизнес-обследования и получены следующие результаты:
|
|
|
| Интервалы значений показателя деловой активности (в баллах) | 0 - 8 | 8 - 16 | 16 - 24 | 24 - 32 |
| Число предприятий (акционерные общества открытого типа) | 10 | 15 | 8 | 5 |
Построить гистограмму распределения частот. Найти среднее значение показателя деловой активности, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Объяснить полученные результаты.
Решение.
| Число предприятий (акционерные общества открытого типа) | Середины интервалов | 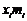
| 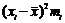
|
| 10 | 4 | 40 | 940,9 |
| 15 | 12 | 180 | 43,35 |
| 8 | 20 | 160 | 317,52 |
| 5 | 28 | 140 | 1022,45 |
| 38 | 520 | 2324,22 |
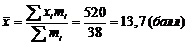
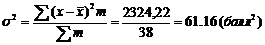
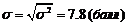
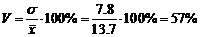
4
Задача №1
В билетном зале 3 кассы. Вероятность того, что с 12 часов до 13 они работают, соответственно равны 0.95, 0.9, 0.85. Составьте закон распределения числа работающих касс в течение этого часа, и вычислите числовые характеристики этого распределения. Какова вероятность того, что будут работать не менее двух касс?
Решение
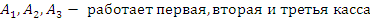

| X – число работающих касс | 0 | 1 | 2 | 3 |
| P(X=m) | 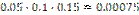
| 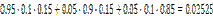
| 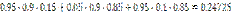
| 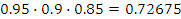
|
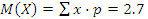
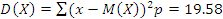

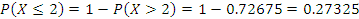
Задача №2
Для оценки числа безработных среди рабочих одного из районов города в порядке случайной повторной выборки отобраны 400 человек рабочих специальностей. 25 из них оказались безработными. Используя 95%-ный доверительный интервал, оцените истинные размеры безработицы среди рабочих этого района.
|
|
|
Решение
n=400, m=25, 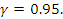
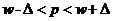
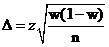
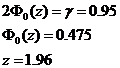
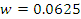
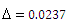
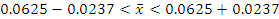
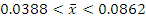
5
Задача №1
Телевизионный канал рекламирует новый вид детского питания. Вероятность того, что телезритель увидит эту рекламу, оценивается в 0,2. В случайном порядке отобраны 10 телезрителей. Составьте ряд распределения числа лиц, видевших рекламу. Найдите числовые характеристики этого распределения. Какова вероятность того, что по крайней мере 2 телезрителя этого канала видели рекламу нового детского питания?
Решение.
Биномиальный закон распределения
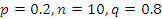
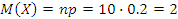 (чел)
(чел)

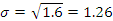
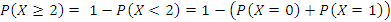
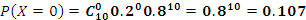
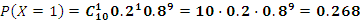

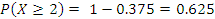
Задача №2
Имеются выборочные данные о числе сделок, заключенных брокерскими фирмами и конторами города в течение месяца:
| Число заключенных сделок | 10-30 | 30-50 | 50-70 | 70-90 |
| Число брокерских фирм и контор | 20 | 18 | 12 | 5 |
Построить гистограмму распределения частот. Найти среднее число заключенных сделок, дисперсию, среднее квадратическое отклонение, коэффициент вариации, размах вариации. Объяснить полученные результаты.
|
|
|
Решение.
| Число брокерских фирм и контор | Середины интервалов | 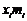
| 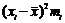
|
| 20 | 20 | 400 | 8569,8 |
| 18 | 40 | 720 | 8,82 |
| 12 | 60 | 720 | 4469,88 |
| 5 | 80 | 400 | 7722,45 |
| 55 | 2240 | 20770,95 |
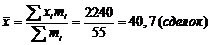
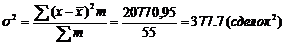
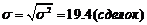
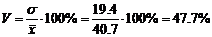
6
Задача №1
Такси обслуживает 3 населенных пункта. Вероятности того, что на остановке будут пассажиры (не более трех), желающих доехать до каждого пункта, соответственно равны 0.9, 0.85, 0.8. Составьте закон распределения числа пассажиров на остановке и вычислите числовые характеристики этого распределения. Какова вероятность того, что пассажиров будет не более двух?
Решение
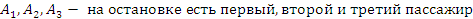
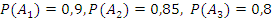
| X – число пассажиров на остановке | 0 | 1 | 2 | 3 |
| P(X=m) | 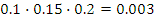
| 0,056 | 0,329 | 0,612 |
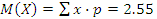
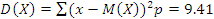
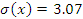
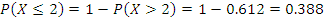
Задача №2
Туристическое бюро, рекламируя отдых на одном из морских курортов, утверждает, что для этого курорта характерна идеальная погода со среднегодовой температурой +20° С. Пусть случайно отобраны 35 дней в году. Какова в этом случае вероятность того, что отклонение средней температуры за отобранные дни от среднегодовой температуры не превысит по абсолютной величине 2°С, если температура воздуха распределена по нормальному закону, а стандартное отклонение дневной температуры составляет 4° С?
Решение.
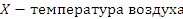
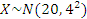
n=35, 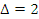
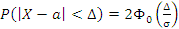
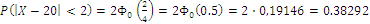 .
.
7
Задача №1
Интегральная функция распределения F(x) непрерывной случайной величины задана следующим образом.
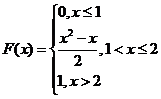
Найти плотность распределения этой случайной величины, вычислить числовые характеристики распределения и построить графики функции распределения и плотности распределения.
Задача №2
Предположим, что на некотором предприятии собраны данные о числе дней, пропущенных работниками по болезни.
| Число дней, пропущенных в текущем месяце | 0 | 1 | 2 | 3 | 4 | 5 |
| Число работников | 10 | 17 | 25 | 28 | 30 | 27 |
Построить полигон распределения частот. Найдите среднее число пропущенных дней, стандартное отклонение, коэффициент вариации. Является ли распределение симметричным?
8
Задача №1
Под руководством бригадира производственного участка работают 3 мужчин и 4 женщины. Бригадиру необходимо выбрать двух рабочих для специальной работы. Не желая оказывать кому-либо предпочтения, он решил выбрать двух рабочих случайно. Составьте ряд распределения числа женщин в выборке. Найдите числовые характеристики этого распределения. Какова вероятность того, что будет выбрано не более одной женщины?
Задача №2
Постройте гистограмму частот, найдите среднюю арифметическую, среднее квадратическое отклонение и коэффициент вариации для данных о дневной выручке в магазине электроники:
| Выручка, у.е. | 0-200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 |
| Число дней | 3 | 5 | 9 | 14 | 8 | 3 |
9
Задача №1
Модельер, разрабатывающий новую коллекцию одежды к весеннему сезону, создает модели в зеленой, черной и красной цветовой гамме. Вероятность того, что зеленый цвет будет в моде весной, модельер оценивает в 0,3, что черный - в 0,2, а вероятность того, что будет моден красный цвет - в 0,15. Предполагая, что цвета выбираются независимо друг от друга, оцените вероятность того, что цветовое решение коллекции будет удачным хотя бы по одному из выбранных цветов?
РЕШЕНИЕ. 1 способ:
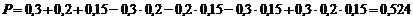
2 способ: 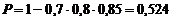
Задача №2 ЗАМЕНИТЬ ЗАДАЧУ
Служащий рекламного агентства утверждает, что время, в течение которого телезрители помнят содержание коммерческого рекламного ролика, подчиняется экспоненциальному закону с 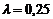 дня. Найдите долю зрителей, способных вспомнить рекламу спустя 7 дней?
дня. Найдите долю зрителей, способных вспомнить рекламу спустя 7 дней?
РЕШЕНИЕ. 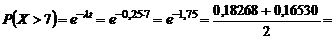 0,17399
0,17399
10
Задача №1
В городе три коммерческих банка, оценка надежности которых - 0,95, 0,9 и 0,85 соответственно. В связи с определением хозяйственных перспектив развития города администрацию интересуют ответы на следующие вопросы: а) какова вероятность того, что в течение года обанкротятся все три банка?; б) что обанкротится хотя бы один банк?
РЕШЕНИЕ.
Соб.(А) – обанкротится 1-й банк
Соб.(В) – обанкротится 2-1 банк
Соб.(С) – обанкротится 3-й банк
События А,В и С – независимые в совокупности
СОБ. (АВС) – обанкротятся все 3 банка.
1. Р(АВС)=Р(А)*Р(В)*Р(С)=0,05*0,1*0,15=0,00075
2. Вероятность появления хотя бы одного события
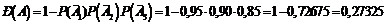
Задача №2 ЭТУ ЗАДАЧУ НУЖНО ЗАМЕНИТЬ, ОЧЕНЬ МНОГО СЧЕТА
Имеются данные о числе тонн грузов, перевозимых еженедельно паромом некоторого морского порта в период навигации: 398, 412, 560, 474, 544, 690, 587, 600, 613, 457, 504, 477, 530, 641, 359, 566, 452, 633, 474, 499, 580, 606, 344, 455, 505, 396, 347, 441, 390, 632, 400, 582.
Составьте вариационный ряд. Найдите среднюю арифметическую. Рассчитайте показатели вариации ряда. Сделайте анализ полученных результатов.
11
Задача №1
Руководство фирмы выделило отделу рекламы средства для помещения в печати объявлений о предлагаемых фирмой товарах и услугах. По расчетам отдела рекламы выделенных средств хватит для того, чтобы поместить объявления только в 15 из 25 городских газет. Сколько существует способов случайного отбора газет для помещения объявлений? Какова вероятность того, что в число отобранных попадут 15 газет, имеющих наибольший тираж?
Задача №2
Для поступления в некоторый университет необходимо успешно сдать вступительные экзамены. В среднем их выдерживают лишь 25% абитуриентов. Предположим, что в приемную комиссию поступило 1889 заявлений. Чему равна вероятность того, что хотя бы 500 поступающих сдадут все экзамены (наберут проходной балл)?
РЕШЕНИЕ.
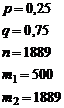
| 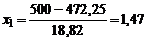 ; ; 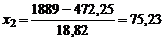
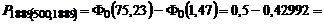  0,07 0,07
|
12
Задача №1
Покупая карточку лотереи “Спортлото”, игрок должен зачеркнуть 6 из 49 возможных чисел от 1 до 49. Если при розыгрыше тиража лотереи он угадает все 6 чисел, то имеет шанс выиграть значительную сумму денег. Сколько возможных комбинаций можно составить из 49 по 6, если порядок чисел безразличен? Чему равна вероятность угадать все шесть номеров?
Задача №2
Авиакомпания знает, что 5% людей, делающих предварительный заказ на определенный рейс, не будут использовать его. Если авиакомпания продала 160 билетов на самолет, в котором лишь 155 мест, чему равна вероятность того, что место будет доступно для любого пассажира, имеющего заказ и планирующего улететь?
РЕШЕНИЕ.
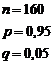
| 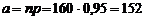
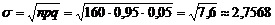
|
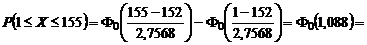
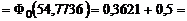 0,8621
0,8621
13
Задача №1
Экономист-аналитик условно подразделяет экономическую ситуацию в стране на “хорошую”, “посредственную” и “плохую” и оценивает их вероятности для данного момента времени в 0,15, 0,70 и 0,15 соответственно. Некоторый индекс экономического состояния возрастает с вероятностью 0,6, когда ситуация “хорошая”; с вероятностью 0,3, когда ситуация “посредственная”, и с вероятностью 0,1, когда ситуация “плохая”. Пусть в настоящий момент индекс экономического состояния возрос. Чему равна вероятность того, что экономика страны на подъеме?
РЕШЕНИЕ.
Событие 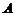 - возрастание индекса экономического состояния
- возрастание индекса экономического состояния
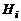 - гипотезы - гипотезы
| 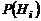
| 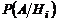
| 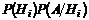
| 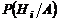
|
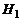 - экономическая ситуация в стране «хорошая» - экономическая ситуация в стране «хорошая»
| 0,15 | 0,6 | 0,090 | 0,2857 |
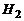 - экономическая ситуация с стране «посредственная» - экономическая ситуация с стране «посредственная»
| 0,7 | 0,3 | 0,210 | |
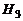 - экономическая ситуация в стране «плохая» - экономическая ситуация в стране «плохая»
| 0,15 | 0,1 | 0,015 | |
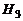 - экономическая ситуация в стране «плохая» - экономическая ситуация в стране «плохая»
| 0,15 | 0,1 | 0,015 | |
| å | 1 | - | 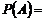 0,315 0,315
|
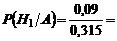 0,2857
0,2857
Задача №2
Администрацию универсама интересует оптимальный уровень запасов продуктов в торговом зале, а так же среднемесячный объем покупок товаров, которые не являются предметом ежедневного потребления в семье (например, таких как сода). Для выяснения этого вопроса менеджер универсама в течение января регистрировал частоту покупок 100 граммовых пакетов с содой и собрал следующие данные (xi): 8, 4, 4, 9, 3, 3, 1, 2, 0, 4, 2, 3, 5, 7, 10, 6, 5, 7, 3, 2, 9, 8, 1, 4, 6, 5, 4, 2, 1, 0, 8.
Постройте вариационный ряд, определите его числовые характеристики. Какие рекомендации Вы дали бы администрации универсама?
14
Задача №1
Из числа авиалиний некоторого аэропорта 60% - местные, 30% - по СНГ и 10% - в дальнее зарубежье. Среди пассажиров местных авиалиний 50% путешествуют по делам, связанным с бизнесом, на линиях СНГ таких пассажиров 60%, на международных - 90%. Из прибывших в аэропорт пассажиров случайно выбирается один. Чему равна вероятность того, что он: а) бизнесмен; б) прибыл из стран СНГ по делам бизнеса; в) прилетел местным рейсом по делам бизнеса; г) прибывший международным рейсом бизнесмен.
Задача №2
Имеются данные о группировке коммерческих банков РФ по величине объявленного уставного фонда:
| Объявленный уставной фонд (руб.) | до 100 млн. | 100-500 млн. | 500 млн. - 1 млрд. | свыше 1 млрд. |
| Число коммерческих банков | 87 | 1075 | 377 | 1004 |
Построить гистограмму распределения частот. Найти средний размер объявленного уставного фонда коммерческих банков РФ. Охарактеризовать колеблемость размеров объявленных уставных фондов коммерческих банков с помощью соответствующих показателей.
15
Задача №1
Четыре человека случайно отбираются из 10 согласившихся участвовать в интервью для выяснения их отношения к продукции фирмы по производству продуктов питания. Эти 4 человека прикрепляются к 4 интервьюерам. Сколько существует различных способов составления таких групп? Если выбор случаен, чему равна вероятность прикрепления определенного человека к интервьюеру?
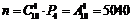
Задача №2
На перекрестке дорог движение регулируется автоматическим светофором, включающим зеленый свет через каждые 2 минуты. Время простоя автомобиля у этого светофора, остановившегося на красный свет, есть случайная величина, распределенная равномерно на интервале (0; 2) минут. Найдите среднее время простоя и среднее квадратическое отклонение.
РЕШЕНИЕ. 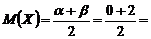 1
1
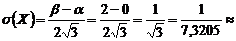 0,5773
0,5773
16
Задача №1
Среди студентов института - 30% первокурсников, 35% студентов учатся на втором курсе, на третьем и четвертом курсе их 20% и 15% соответственно. По данным деканатов известно, что на первом курсе 20% студентов сдали сессию только на отличные оценки, на втором - 30%, на третьем - 35%, на четвертом - 40% отличников. Наудачу вызванный студент оказался отличником. Чему равна вероятность того, что он (или она) - третьекурсник.
Дата добавления: 2018-04-05; просмотров: 1887; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
