Из свойств средней получается формула упрощающая вычисления
ЗАДАЧА 1
В случайном порядке было обследовано 60 участков по показателям водопотребления, куб.м/га:
174 166 174 146 173 165 188 161 150 158
173 164 150 156 142 171 154 175 189 140
157 164 168 171 170 158 186 165 185 172
168 170 163 176 160 172 163 162 178 155
180 162 156 148 160 156 148 150 167 166
154 166 165 181 177 152 145 167 177 185
По данным задачи составить дискретный или интервальный ряд распределения. Построить его графический образ (полигон, гистограмму, кумулятивную кривую, огиву), определить среднюю арифметическую медиану, показатели вариации и коэффициент асимметрии.
Р е ш е н и е
Построим интегральный вариационный ряд распределения – ряд упорядоченных значений варьирующего количественного признака с соответствующими частотами (весами).
Для определения интервалов используется формула Стерджесса
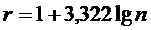 ,
,
где  численность совокупности (при
численность совокупности (при 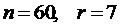 ).
).
Величина интервала или шаг равен
 .
.
При подсчёте частот, т.е. числа вариантов, принадлежащих данному интервалу, используется принцип включительно, который предполагает помещать варианту в тот интервал, где её значение совпадает с правой границей интервала.
| Значения признака | Частоты | Накопленные частоты |
| 140-147 | 4 | 4 |
| 147-154 | 8 | 12 |
| 154-161 | 10 | 22 |
| 161-168 | 16 | 38 |
| 168-175 | 11 | 49 |
| 175-182 | 6 | 55 |
| 182-189 | 5 | 60 |
| Итого | 60 | - |
|
|
|
Строим графический образ полученного ряда распределения. Для дискретного ряда строится полигон, для непрерывного – гистограмма с последующим переходом к полигону.
Полигоном называется ломаная, соединяющая точки плоскости с координатами  , где
, где  значение варьирующего признака,
значение варьирующего признака, 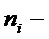 соответствующая частота. Эту ломаную замыкают по оси
соответствующая частота. Эту ломаную замыкают по оси  . Для этого берут два дополнительных варианта, у которых частоты равны нулю.
. Для этого берут два дополнительных варианта, у которых частоты равны нулю.
Для построения гистограммы по оси ОХ откладываются отрезки, изображающие интервалы значений варьирующего признака. На них, как на основаниях, строятся прямоугольники с высотами пропорциональными частотам соответствующих интервалов.
Если соединить середины верхних оснований прямоугольников отрезками, то получим полигон.
Если в прямоугольной системе координат построить точки  , где
, где  значение признака, ординаты – накопленные частоты, то ломаная, соединяющая эти точки, называется кумулятивной кривой.
значение признака, ординаты – накопленные частоты, то ломаная, соединяющая эти точки, называется кумулятивной кривой.
Если точки на плоскости имеют координаты  , то ломаная называется огивой.
, то ломаная называется огивой.
Для интервального ряда в качестве  берут середины интервалов. Точно также строится огива.
берут середины интервалов. Точно также строится огива.
Под формой статистического распределения понимают вид графика полигона или гистограммы.
|
|
|
Распределение называется симметричным, если частоты любых двух вариантов равноотстоящих от некоторого среднего варианта равны (на практике практически равны). Наше распределение, следовательно, симметричное.
Различают также:
а) умеренно асимметричные (левосторонние или правосторонние), т.е. распределения, у которых частоты вариантов, находящихся по одну сторону от наибольшего, больше частот вариантов равноудаленных по другую сторону;
б) крайне асимметричные – частоты вариантов или все время возрастают или убывают;
в) U- образные.
Средней арифметической вариационного ряда, называется сумма произведений всех вариантов на соответствующие им частоты, поделенная на сумму частот

(для интервального ряда 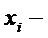 середины интервалов).
середины интервалов).
Из свойств средней получается формула упрощающая вычисления

(в качестве С – берут варианту, приходящуюся на середину вариационного ряда или варианту с набольшей частотой,  шаг интервала).
шаг интервала).
Середины

| Частоты |  С=164,5
С=164,5
| 
| 
|
| 143,5 | 4 | -21 | -3 | -12 |
| 150,5 | 8 | -14 | -2 | -16 |
| 157,5 | 10 | -7 | -1 | -10 |
| 164,5 | 16 | 0 | 0 | 0 |
| 171,5 | 11 | 7 | 1 | 11 |
| 178,5 | 6 | 14 | 2 | 12 |
| 185,5 | 5 | 21 | 3 | 15 |
| Итого | 60 | - | - | 0 |
|
|
|
Тогда,  .
.
Медианой Ме называется вариант, приходящийся на середину вариационного ряда. Для нахождения Ме необходимы накопленные частоты. В случае дискретного ряда и  , если
, если  , то
, то  .
.
В случае интервального распределения, используется допущение, что на каждом интервале варианты распределены равномерно.
В нашем случае  .
.
Оба этих варианта находятся на интервале (161; 168], причём на этом интервале находится 16 вариантов равно отстоящих друг от друга на величину  . Последний вариант предыдущего интервала
. Последний вариант предыдущего интервала  , тогда
, тогда
 ,
,
 ,
,
 .
.
Модой Мо называется наиболее часто встречающийся вариант. Для дискретного распределения этот вариант очевиден, для интервального распределения
 ,
,
где 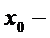 начальное значение модального интервала,
начальное значение модального интервала,
 величина модального интервала,
величина модального интервала,
 частота модального интервала,
частота модального интервала,
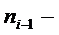 частота предыдущего интервала,
частота предыдущего интервала,
 частота последующего интервала.
частота последующего интервала.
 .
.
Размах вариации  .
.
Средним линейным отклонением называется величина
 .
.
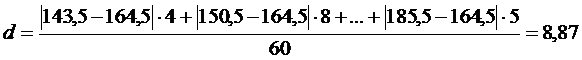 .
.
Дисперсиейвариационного ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической:
|
|
|
 среднее квадратическое отклонение.
среднее квадратическое отклонение.
Из свойств дисперсии вытекает упрощённая формула для её вычисления:
 .
.
Т.о., предыдущая таблица будет дополнена столбцами:
Частоты

| 
|

|

|
| 4 | -3 | 9 | 36 |
| 8 | -2 | 4 | 32 |
| 10 | -1 | 1 | 10 |
| 16 | 0 | 0 | 0 |
| 11 | 1 | 1 | 11 |
| 6 | 2 | 4 | 24 |
| 5 | 3 | 9 | 45 |
| 60 | - | - | 158 |

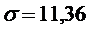 .
.
Центральным моментом вариационного ряда третьего порядка называется
 .
.

Коэффициентом асимметрии называется отношение  .
.
А – является показателем скошенности ряда в ту или иную сторону.
Если  , распределение симметричное,
, распределение симметричное,  положительная (правосторонняя),
положительная (правосторонняя),  отрицательная (левосторонняя) асимметрии.
отрицательная (левосторонняя) асимметрии.
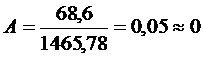 , т.е. распределение практически симметричное.
, т.е. распределение практически симметричное.
Для нахождения  и
и  в таблице достаточно добавить три столбца:
в таблице достаточно добавить три столбца:
 .
.
ЗАДАЧА 2
Считая данные задачи 1 результатом собственно случайной повторной выборки из большой генеральной совокупности, определить:
1) точечные оценки средней и дисперсии в генеральной совокупности,
2) интервальную оценку средней при доверительной вероятности 0,95 ,
3) вероятность того, что ошибка выборочной средней не превосходит 4 м3/га,
4) необходимый объём выборки, чтобы ошибка выборочной средней с вероятностью 0,99 не превышала 1 м3/га.
Р е ш е н и е
Выборочная средняя собственно случайной повторной выборки является случайной величиной, математическое ожидание которой равно генеральной средней  , а дисперсия равна
, а дисперсия равна  , где
, где  - генеральная дисперсия,
- генеральная дисперсия,  объём выборки. Кроме того, выборочная средняя является распределённой по нормальному закону и к ней применима формула этого закона
объём выборки. Кроме того, выборочная средняя является распределённой по нормальному закону и к ней применима формула этого закона
 .
.
При этом можно считать, что выборочная средняя совпадает с генеральной средней,  , а для генеральной и выборочной дисперсий справедливо соотношение
, а для генеральной и выборочной дисперсий справедливо соотношение
 .
.
Если объём выборки достаточно велик (  ) , то
) , то  , и, следовательно, можно положить
, и, следовательно, можно положить
 .
.
1) В качестве точечной оценки генеральной средней необходимо положить выборочную среднюю, которая является состоятельной, несмещённой и эффективной оценкой генеральной средней
 .
.
Выборочная дисперсия 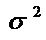 является смещённой оценкой генеральной дисперсии. Несмещённой оценкой является
является смещённой оценкой генеральной дисперсии. Несмещённой оценкой является
 .
.
В нашем случае, при  60 ,
60 , 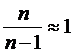 , потому в качестве точечной оценки генеральной дисперсии можно принять величину
, потому в качестве точечной оценки генеральной дисперсии можно принять величину
 .
.
2) По заданной доверительной вероятности находим значение аргумента функции Лапласа
 .
.
Применяя формулу предельной ошибки выборочной средней, находим
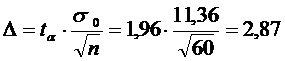 .
.
Таким образом, получаем доверительный интервал
 или
или  ,
,
т.е., с вероятностью 0,95 в генеральной совокупности средний показатель водопотребления находится в границах от 161,63 до 167,37 м3/га.
3) Имеем  . Отсюда
. Отсюда 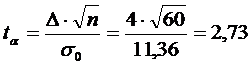 .
.
По таблице интегральной функции Лапласа находим соответствующую доверительную вероятность
 .
.
4) Из  находим
находим  . Преобразовав соответствующим образом формулу предельной ошибки выборки, получаем
. Преобразовав соответствующим образом формулу предельной ошибки выборки, получаем
 .
.
Таким образом, выборочная совокупность должна состоять из не менее 859 участков.
ЗАДАЧА 3
Считая данные задачи 1 результатом собственно случайной повторной выборки из генеральной совокупности, определить:
1) точечную оценку доли участков с показателем водопотребления от 168 до 175 м3/га,
2) доверительный интервал при доверительной вероятности 0,95 ,
3) вероятность того, что ошибка выборочной доли не превысит 0,01 ,
4) необходимый объём выборки, который с вероятностью 0,95 обеспечил бы ошибку выборочной доли не более 0,01 .
Р е ш е н и е
Выборочная доля собственно случайной повторной выборки распределена по нормальному закону. Поскольку вероятность того, что отклонение случайной величины, распределённой по нормальному закону, от её математического ожидания 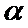 , не превзойдёт по абсолютной величине
, не превзойдёт по абсолютной величине  , равна:
, равна:
 ,
,
где  среднее квадратическое отклонение случайной величины Х , функция
среднее квадратическое отклонение случайной величины Х , функция  функция Лапласа.
функция Лапласа.
Принимая во внимание, что для выборочной доли Z математическое ожидание  , дисперсия
, дисперсия  , т.е.,
, т.е., 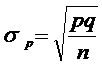 , то
, то
 .
.
1) Находим выборочную долю  . Это и есть точечная оценка генеральной доли
. Это и есть точечная оценка генеральной доли  .
.
2) По заданной доверительной вероятности находим значение аргумента функции Лапласа
 .
.
Применяем формулу предельной ошибки выборочной доли
 .
.
Таким образом, доверительный интервал для генеральной доли Z равен:
 или
или  ,
,
т.е., с вероятностью 0,95 в генеральной совокупности будет от 8 до 28% участков с показателем водопотребления от 168 до 175 м3/га.
3) Имеем  .
.
Отсюда  .
.
По таблице интегральной функции Лапласа находим соответствующую доверительную вероятность  .
.
4) Преобразовав соответствующим образом формулу предельной ошибки выборки, получаем
 ,
,
т.е., сделав случайную выборку в количестве 5670 участков и определив в ней долю участков с показателем водопотребления от 168 до 175 м3/га, можно с практической достоверностью (вероятность 95%) утверждать, что процент данных участков в общем объёме будет близок к проценту данных участков в выборке (отклонение в ту или иную сторону может составить не более 1%).
ЗАДАЧА 4
По эмпирическому распределению, построенному в задаче 1, построить нормальное распределение; изобразить его графически на том же рисунке, на котором построено эмпирическое распределение, а также проверить статистическую гипотезу о нормальности выборочного распределения, используя критерий Пирсона при уровне значимости 0,05 .
Р е ш е н и е
Воспользуемся решением задачи 1 для определения средней и среднего квадратического отклонения в интервальном вариационном ряду:
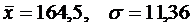 .
.
Нулевую гипотезу сформулируем как утверждение, что случайная величина 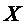 - показатель водопотребления в генеральной совокупности – имеет нормальное распределение с указанными выше параметрами
- показатель водопотребления в генеральной совокупности – имеет нормальное распределение с указанными выше параметрами  .
.
Рассчитаем вероятность  попадания случайной величины
попадания случайной величины 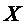 в
в  -ый интервал
-ый интервал  , а затем определим теоретические частоты
, а затем определим теоретические частоты 
 .
.
При этом

для интервального распределения и

для дискретного распределения, где  величина шага дискретного распределения.
величина шага дискретного распределения.
Для упрощённого вычисления теоретических частот используется таблица
Варианты
 - - 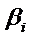
| 
| 
| 
| 
| 
| 

| 
|
| 140-147 | 4 | -1,5401 | -2,1567 | -0,4382 | -0,4886 | 0,0504 | 3 |
| 147-154 | 8 | -0,9243 | -1,5401 | -0,3212 | -0,4382 | 0,117 | 7 |
| 154-161 | 10 | -0,3081 | -0,9243 | -0,1217 | -0,3212 | 0,1995 | 12 |
| 161-168 | 16 | 0,3081 | -0,3081 | 0,1217 | -0,1217 | 0,2434 | 15 |
| 168-175 | 11 | 0,9243 | 0,3081 | 0,3212 | 0,1217 | 0,1995 | 12 |
| 175-182 | 6 | 1,5401 | 0,9243 | 0,4382 | 0,3212 | 0,117 | 7 |
| 182-189 | 5 | 2,1567 | 1,5401 | 0,4886 | 0,4382 | 0,0504 | 3 |
| Итого | 60 | - | - | - | - | - | 59 |
Построим на одном графике теоретические и эмпирические частоты распределения:
Воспользуемся критерием Пирсона в качестве меры расхождения теоретического и эмпирического ряда частот возьмём величину

Случайная величина  имеет специальное распределение, задаваемое таблично, и, зависящее от числа
имеет специальное распределение, задаваемое таблично, и, зависящее от числа  , называемого числом степеней свободы, где
, называемого числом степеней свободы, где  число групп эмпирического распределения,
число групп эмпирического распределения,  число параметров теоретического закона (
число параметров теоретического закона (  ,
, 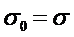 ,
,  ) , т.е.
) , т.е.  . По таблице при уровне значимости
. По таблице при уровне значимости  находим
находим  .
.
Если  , то нулевая гипотеза Н0 (случайная величина имеет нормальное распределение) принимается, если
, то нулевая гипотеза Н0 (случайная величина имеет нормальное распределение) принимается, если  - отвергается.
- отвергается.
В нашем случае  , т.е. случайная величина
, т.е. случайная величина 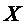 - показатель водопотребления, распределён по нормальному закону.
- показатель водопотребления, распределён по нормальному закону.
ЗАДАЧА 5
Приведены данные по группе хозяйств о дозах внесения удобрений на 1 га посева зерновых в центнерах (Х) и об урожайности зерновых культур в центнерах с 1 га (У). Методом корреляционного анализа исследуйте зависимости между этими признаками. Постройте уравнения регрессии. Рассчитайте коэффициент корреляции и постройте график корреляционной зависимости.
| Х | 4,1 | 3,0 | 3,8 | 1,7 | 0,8 | 3,1 | 2,9 | 0,7 | 3,1 | 3,9 |
| У | 29,2 | 21,9 | 29,6 | 24,3 | 23,4 | 26,0 | 33,1 | 15,3 | 29,8 | 36,2 |
Р е ш е н ие
Все промежуточные расчёты для определения показателей удобно свести в единую таблицу:
| Порядковый номер | Х | У | Х2 | ХУ | У2 |
| 1. | 4,1 | 29,2 | 16,81 | 119,72 | 852,64 |
| 2. | 3,0 | 21,9 | 9,0 | 65,7 | 479,61 |
| 3. | 3,8 | 29,6 | 14,44 | 112,48 | 876,16 |
| 4. | 1,7 | 24,3 | 2,89 | 41,31 | 590,49 |
| 5. | 0,8 | 23,4 | 0,64 | 18,72 | 547,56 |
| 6. | 3,1 | 26,0 | 9,61 | 80,6 | 676,0 |
| 7. | 2,9 | 33,1 | 8,41 | 95,99 | 1095,61 |
| 8. | 0,7 | 15,3 | 0,49 | 10,71 | 234,09 |
| 9. | 3,1 | 29,8 | 9,61 | 92,38 | 888,04 |
| 10. | 3,9 | 36,2 | 15,21 | 141,18 | 1310,44 |
| Итого | 27,1 | 268,8 | 87,11 | 778,79 | 7550,64 |
Тогда  ;
;
 ;
;
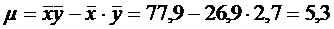 ;
;
 ;
;
 .
.
Находим коэффициенты регрессии
 .
.
Тогда уравнения регрессии  на
на  имеет вид:
имеет вид:
 или
или  ,
,
а уравнение регрессии  на
на  :
:
 или
или  .
.
Построим их на одном чертеже:
Вычислим коэффициент корреляции  .
.
Поскольку  достаточно близок к 1 , то между дозой внесения удобрений на 1 га (Х) и урожайностью (У) имеется тесная линейная корреляционная связь.
достаточно близок к 1 , то между дозой внесения удобрений на 1 га (Х) и урожайностью (У) имеется тесная линейная корреляционная связь.
ЗАДАЧА 6
Приведены результаты конкурсного сортоиспытания зерновых культур А, В, С на четырёх участках. Методом дисперсионного анализа изучить влияние сорта на урожайность. Установить существенность влияния фактора при уровне значимости 0,05 .
| Сорт | Урожайность по повторностям (ц/га) | |||
| А | 35,2 | 35,3 | 32,2 | 33,8 |
| В | 29,7 | 33,1 | 32,8 | 29,6 |
| С | 52,5 | 50,1 | 53,8 | 47,6 |
Р е ш е н и е
Схему анализа можно представить следующим образом:
| Варианты (сорт) | Урожайность по повторностям | Суммы
| Средняя
| |||
| I | П | Ш | IY | |||
| А | 35,2 | 35,3 | 32,2 | 33,8 | 136,5 | 34,1 |
| В | 29,7 | 33,1 | 32,8 | 29,6 | 125,2 | 31,3 |
| С | 52,5 | 50,1 | 53,8 | 47,6 | 204 | 51 |
| Сумма по вариантам | 117,4 | 118,5 | 118,8 | 111 | 465,7 | 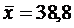
|
На основании приведённых данных находим общую дисперсию:
 = (35,2-38,8)2 + (35,3-38,8)2 + … + (47,6-38,8)2 = 947,5 .
= (35,2-38,8)2 + (35,3-38,8)2 + … + (47,6-38,8)2 = 947,5 .
Групповая дисперсия будет равна:
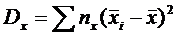 = 4(34,1-38,8)2 + 4(31,3-38,8)2 + 4(51-38,8)2 = 908,7 .
= 4(34,1-38,8)2 + 4(31,3-38,8)2 + 4(51-38,8)2 = 908,7 .
Тогда, остаточная дисперсия будет равна
 = 947,5-908,7 = 38,8 .
= 947,5-908,7 = 38,8 .
Рассчитаем дисперсии, приходящиеся на одну степень свободы:
 ,
,
 ,
,
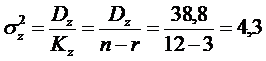 .
.
Для определения достоверности влияния находим  при
при  , так как
, так как  , то влияние сорта на урожайность существенно.
, то влияние сорта на урожайность существенно.
Дата добавления: 2018-04-05; просмотров: 140; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!


