Корни должны быть отрицательными числами, если корни получились комплексными, то они должны иметь отрицательную вещественную часть
Решение (4.5) с учетом п.5 запишем следующим образом:
(4.7)
Продифференцируем это уравнение:
. (4.8)
8. Вычислим постоянные интегрирования 
и 
. Для этого запишем (4.7) и (4.8) для времени 
подставив в них численные значения начальных условий.
Решая эту систему, найдем: 
, 
. Подставим вычисленные величины в правую часть уравнения (4.7) и получим решение
A. (4.9)
9. Расчет остальных токов и напряжений на реактивных элементах и построение графиков.
Подставим (4.9) в систему (4.1) и найдем остальные токи:
A,
и напряжения на конденсаторе и на катушки индуктивности:
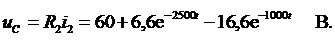
Данные расчетов сведены в табл. 4.3. На рис. 4.80 приведены соответствующие графики на временном интервале:
|
| Рис. 4.80 |
Величина временного интервала выбирается равной 
, где 
, если корни характеристического уравнения вещественные числа, в случае комплексных корней расчет выполняется на временном интервале, равном не менее трем периодам колебаний токов и напряжений.
Таблица 4.3
| № | t | iL(t) | i2(t) | iC(t) | uC(t) |
| c | A | A | A | В | |
| 1 | +0 | 0,260 | 0,250 | 0 | 50,0 |
| 2 | 0,4×10-3 | 0,307 | 0,256 | 0,050 | 51,3 |
| 3 | 0,8×10-3 | 0,319 | 0,267 | 0,052 | 53,2 |
| … | … | … | … | … | … |
| 8 | 3,0×10-3 | 0,304 | 0,296 | 0,008 | 59,2 |
Задачу можно было решить, не решая дифференциального уравнения (4.2). Общее решение для тока может быть сразу представлено в виде:
|
|
|
.
Корни характеристического уравнения определяются, используя матрицу контурных сопротивлений:
|
или матрицу узловых проводимостей ( 
). Источник напряжения закорочен.
Оба уравнения дают одно и тоже решение:
, 
.
Затем можно записать
.
Дальнейшее решение совпадает с рассмотренным ранее.
Операторный метод
Рассчитаем начальные условия для переменных:
, 
.
Эти величины используются при написании уравнений цепи в операторной форме. Согласно законам Кирхгофа запишем следующую систему уравнений в операторной форме:
Подставим численные значения в данную систему
Приведем систему к операторному уравнению относительно операторного тока 
и сравним с ранее полученным решением
,
где A(p) – полином числителя иB(p) – полином знаменателя.
Рекомендуется проверить правильность полученного уравнения с помощью пределов:
.
Рассчитанные токи 
и 
совпадают с соответствующими токами, полученными по классическому методу.
Чтобы рассчитать ток 
будем использовать теорему разложения:
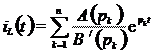. (4.10)
|
|
|
1. Найдем корни из уравнения B(p)=0
.
, 
, 
.
2. Произведем дифференцирование
.
3. Рассчитаем коэффициент 
для корня 
:
4. Рассчитаем коэффициент для корня 
:
5. Рассчитаем коэффициент для корня 
:
6. Используя (4.10), получаем формулу для тока:
A.
Эта формула совпадает с выражением (4.9) для 
, полученным классическим методом. Токи в других ветвях и напряжение на реактивных элементах получают по аналогии.
Дата добавления: 2018-04-05; просмотров: 584; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!