Выбор операторного уравнения и структуры процессорных

Измерительных средств.

       Выбор операторного уравнения и структуры ПрИС осуществляется в соответствии с алгоритмом (Рис.3.8) (блоки 1 16), реализующим первый этап структурной модели (Рис.3.6). Пример выбора рассмотрен на основе параметров и признаков технологического процесса, включая операции О1, Р1, З1, С1 (Рис. 3.7). Из множества параметров и признаков технологических операций формируется упорядоченный ряд (блок 2) для технологического процесса

                              М_тп = < X₁, X₂, X₃, X₄, X₅, X₆, X₈, X₁₀ >                   (3.1)

На основе упорядоченного ряда формируются эталонные множества (Блок 3, рис. 3.8), определяющие операторные уравнения, для каждого измеряемого параметра, для данного примера измеряемыми параметрами являются диаметр и длина древесного сырья (хлысты, сортименты). Принцип формирования эталонных множеств описан ниже.

Х1 Х2 Х4 Х5 Х7 Х8 Х10

Х1 Х2 Х4 Х5 Х7 Х8 Х10

Х1 Х3 Х4 Х5 Х6 Х7 Х8

Х1 Х3 Х4 Х5 Х6 Х7 Х8

П а р а м е т р ы и п р и з н а к и т е х н о л о г и ч е с к и х о п е р а ц и й

О1

Р1

З1

С1

 

Рис. 3.7. Технологические операции, параметры и признаки технологических операций.

 

Начало

 

Исходные данные: -технологические операции -параметры и признаки техно- логических операций

                     1       

 

 

Формирование упорядоченного ряда параметров и признаков технологического процесса

               2 

 

 

 

Формирование эталонных множеств, определяющих операторные уравнения при измерении параметров объекта

               3

 

 

Формирование симметричной матрицы расстояний между эталонными множествами

 

                4 

Определение порогового расстояния между эталонными множествами

 

                        

                5 

Формирование построчных кластеров симметричной матрицы расстояний между эталонными множествами

 

 

                6

Определение среднегруппового расстояния между эталонными множествами:

 

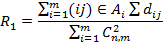
                  7   

 

                                                                                                  

Проверка эталонных множеств на разнородность

                8                

                  

Эталонные множества разнородные?

                                       9                                                             

                       Да                                                                           Нет       

9

10

 

 

                                     10

Формирование множеств параметров и признаков технологических операций, соответствующих измеряемым параметрам

                                          

 

 

                                      11                                                                                                                  

Формулирование матрицы расстояний между множествами технологических операций и эталонными множествами

                                                                                                            

 

 

                                         

Определение порогового расстояния между множествами технологических операций и эталонными множествами: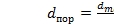

                                    12  

 

 

 

                                  13

Формирование построчных кластеров матрицы расстояний между множествами технологических операций и эталонными множествами

                                     

 

 

                                  

                    

Определение среднегруппового расстояния между множествами технологических операций и эталонными множествами: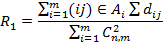

                                    14

                                   

 

        

                                      

                                    15

Определение построчных сходных множеств матрицы расстояний между множествами технологических операций и эталонными множествами.

                                      

 

 

 

                                    16

Формирование таблицы результатов выбора операторных уравнений и структуры процессорных измерительных средств

                                      

                                     

 

 

                                    

 

Конец

 

 

Pис. 3.8. Алгоритм выбора операторного уравнения и структуры процессорных измерительных средств.

       В каждое эталонное множество в качестве элементов множества при измерении диаметра входят: объект измерения (Х₁), признак состояния поверхности (X₂ или X₃), способ перемещения объекта в зоне измерения (X₄ или X₁₃), способ подачи объекта измерения (X₅ или X₂₁), наличие или отсутствие ориентации объекта в зоне измерения (X₈ или X₉), один из базовых диаметров (X₆ или X₁₀, или X₁₁, или X₁₂). При этом в эталонное множество не должны одновременно входить два взаимоисключающих признака (X₂ и X₂), (X₄ и X₁₃), (X₅ и X₂₁), (X₈ и X₉) и два базовых диаметра (X₆, X₁₀, X₁₁, X₁₂).

Такой же подход – при формировании эталонных множеств при измерении следующего параметра, в данном случае длины хлыстов или сортиментов. Соответствие эталонных множеств операторным уравнениям определяется с помощью табл. 3.3, 3.4.

Т а б л и ц а 3.3.

Множества, определяющие операторные уравнения при измерении

диаметров

Уравнения	Множества
Косвенные обыкновенные неитеративные измерения (КОНИ)	X1, X3, X4, X5, X6, X8 X1, X3, X4, X5, X8, X10 X1, X3, X5, X6, X8, X11 X1, X3, X5, X8, X10, X11
Косвенные усредненные неитеративные измерения (КУНИ)	X1, X2, X4, X5, X6, X8 X1, X2, X4, X5, X8, X10 X1, X2, X5, X6, X8, X11 X1, X2, X5, X8, X10, X11
Косвенные обыкновенные итеративные измерения (КОИИ)	X1, X3, X4, X5, X6, X9 X1, X3, X4, X5, X9, X10 X1, X3, X5, X6, X9, X11 X1, X3, X5, X9, X10, X11
Косвенные усредненные итеративные измерения (КУИИ)	X1, X2, X4, X5, X6, X9 X1, X2, X4, X5, X9, X10 X1, X2, X5, X6, X9, X11 X1, X2, X5, X9, X10, X11

 

В данном примере X₁₁ соответствует X₁₃, т.е. соответствует поперечному перемещению объекта в зоне измерения. При определении соответствия эталонных множеств операторным уравнениям при измерении диаметров учитывается следующее: обыкновенные измерения – измерения, при которых результат соответствует моменту измерения (разовое измерение). При измерении диаметров это соответствует измерению окоренной (чистовой) поверхности лесоматериала (X₃). Усредненные измерения – измерения, при которых результат измерения соответствует временному интервалу измерения (несколько измерений для повышения точности результата), что соответствует измерению неокоренной (черновой) поверхности (X₂).

Т а б л и ц а 3.4.

Множества, определяющие операторные уравнения при измерении длины.

Уравнения	Множества
Косвенные обыкновенные неитеративные измерения (КОНИ)	X1, X2, X4, X5, X7, X8 X1, X3, X4, X5, X7, X8 X1, X2, X5, X7, X8, X11 X1, X3, X5, X7, X8, X11

 

Итеративные измерения – измерения, при которых выполняются циклы измерений с целью сравнения и выделения требуемых размеров, что соответствует выделению в процессе измерений необходимого базового диаметра (X₆, X₁₀) при неориентированной подаче в зоне измерения (X₉). Неитеративные измерения – измерения, при которых нет необходимости выполнения циклов измерения, что соответствует ориентированной подаче в зоне измерения (X₈).

В данном случае измерения на основе светооптических преобразователей являются косвенными (с промежуточными преобразованиями), поэтому рассматривается выбор уравнения и структуры ПрИС для косвенных измерений.

Число сочетаний эталонных множеств определяется числом взаимоисключающих признаков и базовых диаметров. С учетом изложенного и множества (3.1) сформированы эталонные множества, определяющие выбор операторных уравнений при измерении значений диаметров (табл. 3.5).

Т а б л и ц а 3.5.

Эталонные множества, определяющие операторные уравнения при измерении диаметров.

Эталонные множества	Операторные уравнения
МЭ1 = {X1, X2, X4, X5, X6, X8}	Косвенные усредненные неитеративные измерения
МЭ2 = {X1, X3, X4, X5, X6, X8}	Косвенные обыкновенные неитеративные измерения
МЭ3 = {X1, X2, X4, X5, X10, X8}	Косвенные усредненные неитеративные измерения
МЭ4 = {X1, X3, X4, X5, X10, X8}	Косвенные обыкновенные неитеративные измерения

 

При измерении длины на результат измерения не влияет состояние поверхности объекта измерения, т.к. значение длины определяется наличием объекта в зоне измерения (наличием измерительного сигнала в зоне сканирования светооптических преобразователей).

 Поэтому различным сочетаниям элементов эталонных множеств соответствуют косвенные обыкновенные неитеративные измерения (табл. 3.6).

 

 

Т а б л и ц а 3.6.

Эталонные множества, определяющие операторные уравнения

при измерении диаметров.

Эталонные множества	Операторные уравнения
= {X1, X2, X4, X5, X7, X8}	Косвенные обыкновенные неитеративные измерения
= {X1, X3, X4, X5, X7, X8}	Косвенные обыкновенные неитеративные измерения

 

       Сформированные эталонные множества необходимо проверить на

разнородность для исключения неопределенности при выборе операторного уравнения. С этой целью формируется симметричная матрица расстояний между множествами (блок 4, рис. 3.8). Строки и столбцы матрицы соответствуют эталонным множествам

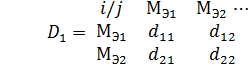                                                          (3.2)

                                                   

Элементы матрицы определяются на основе выражения

                                                                                 (3.3)

где i = М_Э1, М_Э2, …, М_Эm; j =М_Э1, М_Э2, …, М_Эm;

Числитель отражает число общих элементов множеств, знаменатель суммарное число разных элементов. Расстояние  = 0, если элементы двух множеств совпадают, и равно единице, если два множества не имеют ни одного общего элемента.

Для рассматриваемого примера матрица расстояний на основе (3.2, 3.3)

 

	i/j	МЭ1	МЭ2	МЭ3	МЭ4
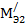
	МЭ1	0	0,29	0,29	0,5	0,29	0,5
	МЭ2	0,29	0	0,5	0,29	0,5	0,29
D1 =	МЭ3	0,29	0,5	0	0,29	0,29	0,5
	МЭ4	0,5	0,29	0,29	0	0,5	0,29
		0,29	0,29	0,29	0,5	0	0,29
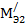
		0,5	0,29	0,5	0,29	0,29	0

 На основе данных матрицы D₁ определяется пороговое расстояние между множествами (блок 5)

dпор. = 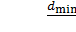 = 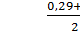0,395 C учетом порогового расстояния формируются построчные кластеры, элементами которых являются множества, расстояния между которыми меньше или равно пороговому расстоянию dij  dпор. (блок 6).

	i/i	МЭ1	МЭ2	МЭ3	МЭ4
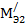
	МЭ1	0	0,29	0,29	0,5	0,29	0,5
	МЭ2	0,29	0	0,5	0,29	0,5	0,29
D1 =	МЭ3	0,29	0,5	0	0,29	0,29	0,5
	МЭ4	0,5	0,29	0,29	0	0,5	0,29
		0,29	0,5	0,29	0,5	0	0,29
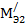
		0,5	0,29	0,5	0,29	0,29	0

 

К₁ = { М_Э1, М_Э2, М_Э3,                                                                                            

К₂ = { М_Э2, М_Э1, М_Э4,

К₃ = { М_Э3, М_Э1, М_Э4,

К₄ = { М_Э4, М_Э2, М_Э3, (3.4)

К₅ = { , М_Э1, М_Э3,

К₆ = { , М_Э2, М_Э4,

 

На основе матрицы расстояний и выделенных построчных кластеров (3.4) формируются группы сходных и разнородных множеств. Для оптимизации разбиения этих групп используется среднегрупповое расстояние (блок 7)

                                                                                

                                   

l  = 1, 2 …, m – число кластеров; A_l – число пар множеств, входящих в кластеры, расстояние между которыми удовлетворяет условию d_ij  d_пор.; d_ij – расстояние между парами множеств A_l, входящих в кластер;  - число внутригрупповых расстояний в кластере; n – число элементов (множеств) в кластере. Суммарное расстояние между парами множеств, входящих в кластеры и удовлетворяющих условию d_ij  d_пор.

 

= d_Э1,Э2 + d_Э1,Э3 +  = 0,29 + 0,29 + 0,29 = 0,87

= d_Э2,Э1 + d_Э2,Э4 +  = 0,29 + 0,29 + 0,29 = 0,87

= d_Э3,Э1 + d_Э3,Э4 +  = 0,29 + 0,29 + 0,29 = 0,87

 

Соответственно для кластеров К₄, К₅, К₆ - = 0,87, = 0,87, = 0,87

В целом, в соответствии с (3.5), суммарное расстояние по всем построчным кластерам

S_k = + + 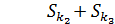= 5,22

Число внутригрупповых расстояний в кластерах К₁  К₆

 

 = 3 + 2 + 1 = 6;  = 3 + 2 + 1 = 6;  = 3 + 2 + 1 = 6;

 = 3 + 2 + 1 = 6;  = 3 + 2 + 1 = 6;  = 3 + 2 + 1 = 6;

Суммарное число внутригрупповых расстояний по всем кластерам

 =  +  +  +  + +  = 36

В результате среднегрупповое расстояние равно

R =  = 0,145

       С учетом данных матрицы D₁ и среднегруппового расстояния эталонные множества проверяются на разнородность (блок 8, 9). Множества являются разнородными при условии, что расстояние между ними большe среднегруппового расстояния, d_ij > R. В данном случае эталонные множества являются разнородными.

      Для выбора операторных уравнений и структуры ПрИС для технологических операций необходимо сформировать множества параметров и признаков этих операций относительно измеряемых параметров (блок 10), на основе исходных данных технологического процесса (рис. 3.7).

 

М_О1 = { X₁, X₂, X₄, X₅, X₈, X₁₀}

М_Р1 = { X₁, X₂, X₄, X₅, X₈, X₁₀}

М_З1 = { X₁, X₃, X₄, X₅, X₈, X₆}

                                   М_С1 = { X₁, X₃, X₄, X₅, X₈, X₆}                           (3.6)

= { X₁, X₂, X₄, X₅, X₇, X₈}

= { X₁, X₂, X₄, X₅, X₇, X₈}

= { X₁, X₃, X₄, X₅, X₇, X₈}

= { X₁, X₃, X₄, X₅, X₇, X₈}

 

        Для выделения сходных множеств и соответствующих им операторных уравнений необходимо сформировать матрицу расстояний D₂ = , строки матрицы соответствуют технологическим множествам (3.6), столбцы – эталонным множествам (табл. 3.5, 3.6).

 

	i/i	МЭ1	МЭ2	МЭ3	МЭ4
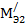
	МО1	0,29	0,5	0	0,29	0,29	0,5
	МР1	0,29	0,5	0	0,29	0,29	0,5
D2 =	МЗ1	0,29	0	0,5	0,29	0,5	0,29
	МС1	0,29	0	0,5	0,29	0,5	0,29
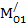
		0,29	0,5	0,29	0,5	0	0,29
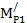
		0,29	0,5	0,29	0,5	0	0,29
		0,5	0,29	0,5	0,29	0,29	0
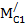
		0,5	0,29	0,5	0,29	0,29	0

 

К₁ = {М₀₁, М_Э3                                                                                            

К₂ = {М_Р1, М_Э3

К₃ = {М_З1, М_Э2

К₄ = {М_С1, М_Э2

К₅ = {

К₆ = {

К₇ = {

 К₈ ={   

         

       Пороговое расстояние между множествами технологических операций и эталонными множествами (блок 12)

 

d_пор. = 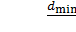 = 0,25

 

По данным матрицы D₂ формируются построчные кластеры (блок 13) К₁  К₈ при условии d_ij  d_пор.

       Для выделения сходных множеств матрицы D₂ необходимо определить среднегрупповое расстояние в соответствии с (3.5) (блок 14). Суммарное расстояние между множествами, входящих в кластеры и удовлетворяющих условию d_ij  d_пор.

= = 0; = = 0; = = 0; = = 0;

= = 0; = = 0; = = 0; = = 0;

 

Суммарное расстояние по всем построчным кластерам

S_k = + + 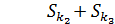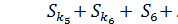0

 

Число внутригрупповых расстояний в кластерах К₁  К₈

 = 1;  = 1;  = 1;  = 1;  =1;  =1;  =1;  =1;

 

Суммарное число внутригрупповых расстояний по всем кластерам

=  +  +  +  +  +  + +  = 8

 

В результате среднегрупповое расстояние равно

R =  = 0

 

      Сходные построчные множества матрицы D₂ и соответствующие им операторные уравнения и структуры ПрИС определяются по условию

 d_ij R (блок 15).

 

 М_СХ1  = {М₀₁, М_Э3  - косвенные усредненные неитеративные измерения                                                                                           

М_СХ2= {М_Р1, М_Э3 - косвенные усредненные неитеративные измерения

М_СХ3= {М_З1, М_Э2  - косвенные обыкновенные неитеративные измерения

М_СХ4= {М_С1, М_Э2  - косвенные обыкновенные неитеративные измерения

М_СХ5= {  - косвенные обыкновенные неитеративные измерения

М_СХ6= {  - косвенные обыкновенные неитеративные измерения

М_СХ7 = {  - косвенные обыкновенные неитеративные измерения

 М_СХ8={  - косвенные обыкновенные неитеративные измерения.

 

В соответствии с выделенными сходными множествами формируется результирующая табл. 3.7.

Выделенным операторным уравнениям соответствуют структуры процессорных измерительных средств (Рис.3.2). После выбора операторного уравнения структуры процессорных измерительных средств необходимо осуществлять выбор оптимального варианта первичных светооптических преобразователей.

Т а б л и ц а 3.7.

Операторные уравнения процессорных измерительных средств при измерении диаметра и длины при автоматизации технологических операций обработки древесного сырья

 

Технологические операции	Сходные множества	Операторные уравнения
		При измерении диаметра	При измерении длины
Очистка дере-вьев от сучьев, О1	МСХ1 = М01, МЭ3	Косвенные усредненные неитеративные измерения
	МСХ5=		Косвенные обыкно-венные неитеративные измерения
Раскряжевка хлыстов, Р1	МСХ2= МР1, МЭ3	Косвенные усредненные неитеративные измерения
	МСХ6=		Косвенные обыкно-венные неитеративные измерения
Зачистка и частичная окорка круглых лесоматериалов, З1	МСХ3= МЗ1, МЭ2	Косвенные обыкновенные неитеративные измерения
	МСХ7 =		Косвенные обыкно-венные неитеративные измерения
Сортировка круглых лесоматериалов, С1	МСХ4 = МС1, МЭ2	Косвенные обыкновенные неитеративные измерения
	МСХ8 =		Косвенные обыкно-венные неитеративные измерения

 

---

Дата добавления: 2018-04-05; просмотров: 309; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!