Геометрический смысл теоремы Лагранжа
ВОПРОСЫ К ЭКЗАМЕНУ ПО КУРСУ МАТЕМАТИЧЕСКИЙ АНАЛИЗ ДЛЯ СТУДЕНТОВ СПЕЦИАЛЬНОСТИ ММ-11
1. Предмет математического анализа.
изучает зависимость между 2-мя или несколькоми переменными при их совместном единении. Основной объект – функция, первичное понятие - переменная величина, функция. Основной аппарат мат. Анализа – дифференциальные и интегральные исчесления. В основе МА лежит теория предела.
2. Элементы теории множеств.
Множество – совокупность или объединение предметов объединенных по любому признаку. Большие буквы – множ,мален-элементы множ. [-1;1]-сегмент,(-1;1) –интервал,( объединен,пересеч,разность,симетр.разность)
3. Отображение функции.
Отображение функции. Функция f (отображение, операция, оператор) — это закон или правило, согласно которому каждому[3] элементу x из множестваX ставится в соответствие единственный элемент y из множества Y.[4]При этом говорят, что функция f задана на множестве X, или что f отображает X в Y.
Если элементу  сопоставлен элемент
сопоставлен элемент  , то говорят, что элемент y находится в функциональной зависимости f от элемента x. При этом переменная x называется аргументом функции f или независимой переменной, множество X называетсяобластью задания или областью определения функции, а элемент y, соответствующий конкретному элементу x — частным значением функции f в точке x. Множество Y всех возможных частных значений функции f называется её областью значений илиобластью изменения
, то говорят, что элемент y находится в функциональной зависимости f от элемента x. При этом переменная x называется аргументом функции f или независимой переменной, множество X называетсяобластью задания или областью определения функции, а элемент y, соответствующий конкретному элементу x — частным значением функции f в точке x. Множество Y всех возможных частных значений функции f называется её областью значений илиобластью изменения
|
|
|
4. Способы задания функций.
когда область определения состоит из конечного числа элементов,описательная-график построить нельзя,переодическая имеет разрыв в каждой точке.графический,аналетический,функция явно заданна и не явно заданна,параметрически,когда х и у заданы как функции промеж перемен t,полярное задание фун-ции
5. Мощность множеств.
это обобщение понятия кол-ва элем на случайн бесконечн множ-во m(A)-мощн от А. множ эквивал множ натур чисел наз-ся счетным. Св-ва счетн множеств1-всякое бескон подмножество счетного множ-ва счетно 2-объедин конечного или счетного числа счетных множ-в счетно
6. Точные верхние и точные нижние грани числовых множеств.
верхняя грань (супремум(sup)) называется число, которое равно или больше всех элементов упорядочного множестава.
нижняя грань (инфимум(inf)) называется число, которое равно или меньше всех элементов упорядочного множества.
S={1/k | kcN} = {1,1/2,1/3,....} sup S=1 inf S=0; выше 1 нету, ниже 0 нету,т.е верняя и нижняя грань.
7. Предел числовой последовательности. Ограниченные и неограниченные числовые последовательности. Монотонные числовые последовательности.
предел числовой последовательности — это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины.
|
|
|
Функция f(x) имеет предел A в точке x0, если для всех значений x, достаточно близких к x0, значение f(x) близко к A.
Число называется пределом числовой последовательности , если последовательность является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.
Ограниченная сверху последовательность — это последовательность элементов множества X, все члены которой не превышают некоторого элемента из этого множества. Этот элемент sup
Ограниченная снизу последовательность — это последовательность элементов множества X, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент inf
Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу.
Неограниченная последовательность — это последовательность, которая не является ограниченной.
Монотонная последовательность — это невозрастающая, либо неубывающая последовательность
|
|
|
Невозрастающая - это последовательность, в которой каждый последующий элемент не превышает предыдущий. Xn >Xn+1
Неубывающая - это последовательность, в которой каждый элемент не превосходит последующий. Xn<Xn+1
8. Бесконечно малые числовые последовательности. Свойства бесконечно малых числовых последовательностей.
Бесконечно малая последовательность — это последовательность, предел которой равен нулю..Свойства 1бесконечно малых последовательностей. Сумма 2 бесконечно малых послед сама является бесконечно малой послед следствие- Разность двух бесконечно малых послед есть бесконечно малая послед.2произ БМ на огранич есть БМ след2-произв БМ посл на схо-ся есть посл БМ след-вие3 произв 2х послед и люб кон БМ числ посл есть БМ посл;3связь между БМ и ББ:пусть  -БМЧП след-но
-БМЧП след-но  -ББЧП верно и обратное;4 крит сход
-ББЧП верно и обратное;4 крит сход  -БМЧП док-ва
-БМЧП док-ва
9. Сходящиеся числовые последовательности. Основные теоремы о сходящихся числовых последовательностях.
Если предел ЧП явл число-послед явл сх-ся основ теоремы10  док-во
док-во 
 -сх-сяслед-но только когда посл сх-ся
-сх-сяслед-но только когда посл сх-ся 
3  4)
4) 

10. Теоремы о предельном переходе в равенство и неравенство.


Следствие 

11. Предел монотонной числовой последовательности. Число е.
|
|
|
 Всякая монотонная ЧП имеет предел,ее предел конечен т.е. она сходится если ЧП ограничена,расходится если ее предел =
Всякая монотонная ЧП имеет предел,ее предел конечен т.е. она сходится если ЧП ограничена,расходится если ее предел =  .Введение числа е связанно с рассмотрением ЧП с общим членом
.Введение числа е связанно с рассмотрением ЧП с общим членом  ;
; 

12. Принцип сходимости числовой последовательности.
Если хn сходится к числу а,то и любая ее подпоследовательность так же схожится к числу а,ечли хn сходиться к  ,то любая ее подпосл имеет
,то любая ее подпосл имеет 
 из всякой сход-сти послед можно извл монотон сход подпосл
из всякой сход-сти послед можно извл монотон сход подпосл
13. Предельные точки числовой последовательности. Верхний и нижний пределы числовой последовательности.
Число А называется предельной точкой чп, если есть в любой её Е окрестности содержится 8 много членов. Отличие от предела состоит в том, что нас не интересует сколько членов за пределами Е.
Если а - предел => а-предельная точка; Xn=(-1)^n - предельные точки -1 и 1
Наибольшую из всех предельных точек чп называют верхним пределом./наименьшую из предельных - нижним
Точка А явл.предельной <=> когда из последовательности Xn можно извлеч подпоследовательность Xa.
Если сходится, последовательность имее предельную точку из определение верхнего и нижнего предела => lim X- сущ => верх и ниж точки равны
Xn - сх-ся <=> Xn огр. верх=нижн
Док-во:
Н: Если Xn-сход, то имеет одну пред точку => пределы совпадают
Д: Т.к Xn огран, то сущ. верх и ниж пределы и они конечны, а по условию они равны =>
Xn имеет единую точку => она сходится.
14. Фундаментальные числовые последовательности. Свойства фундаментальных числовых последовательностей.

Св-ва -для всякой фунд-ой послед,все члены этой послед,за искл некоторого числа сод-ся в интервале 
-всякая фунд-ая ЧП явл ограниченной.
15. Предел функции. Геометрический смысл предела. Односторонние пределы.
Определение по Коши
b=lim(f(x))<=>(AE>0)(Эбе>0)(AxЄ Д(f)|0<|x-x0|<б):
|f(x)-b|<Е
для любого Е>0 и для любых точек х функции выполняется условие |0<|x-x0|<б|
Геометрический смысл:Какую бы горизонтальную Е полосу с центром в точке b мы не взяли бы, найдётся вертикальная б полоса с центром в точке b, такая что все точки f(x), за исключением (x0;f(x0)) попадающие в вертикальную б полосу будут находится в горизонтакльной Е полосе.
Односторо́нний преде́л — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).
Число  называется правосторонним пределом (правым пределом, пределом справа) функции
называется правосторонним пределом (правым пределом, пределом справа) функции  в точке
в точке  , если для всякого положительного числа
, если для всякого положительного числа  отыщется отвечающее ему положительное число
отыщется отвечающее ему положительное число  такое, что для всех точек
такое, что для всех точек  из интервала
из интервала  справедливо неравенство
справедливо неравенство  .
.

Число  называется левосторонним пределом (левым пределом, пределом слева) функции
называется левосторонним пределом (левым пределом, пределом слева) функции  в точке
в точке  , если для всякого положительного числа
, если для всякого положительного числа  отыщется отвечающее ему положительное число
отыщется отвечающее ему положительное число  такое, что для всех точек
такое, что для всех точек  из интервала
из интервала  справедливо неравенство
справедливо неравенство  .[1]
.[1]
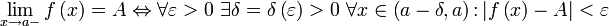
16. Первый замечательный предел.
 Доказательство:
Доказательство:

Рассмотрим односторонние пределы  и
и  и докажем, что они равны 1.Пусть
и докажем, что они равны 1.Пусть  . Отложим этот угол на единичной окружности (R = 1).Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.
. Отложим этот угол на единичной окружности (R = 1).Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.
Очевидно, что:  (1)(где SsectOKA — площадь сектора OKA)
(1)(где SsectOKA — площадь сектора OKA)

 ,
,  (из
(из  : | LA | = tgx)
: | LA | = tgx)
Подставляя в (1), получим:
 Так как при
Так как при  :
: 
Умножаем на sinx: 
Перейдём к пределу:
 ,
,  ,
, 
Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
17. Замечательные пределы для степенной, показательной и логарифмической функций.
Замеч.предел для логарифмической ф-ии

Докажем:

Замечательный предел для степенной функции


Докажем:
 =
= 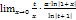 =
=  ,
, 
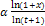 =1
=1
Замечательный предел для показательной функции:

Докажем:
 X=
X= 
18. Предел алгебраической суммы, произведения и частного.
Предел алгебраической суммы, произведения и частного
Бесконечно малые величины и их свойства
Переменная величина называется бесконечно малой величиной (БМВ), если в процессе своего изменения она делается и остается по абсолютной величине меньше любого положительного числа 
Пример бесконечно малой величины: пусть  при n. Зададим
при n. Зададим  При n 1001
При n 1001 
Свойства бесконечно малых величин.


 Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
Пусть , , — бесконечно малые величины, тогда + – — тоже бесконечно малая.
2. Произведение конечного числа на бесконечно малую величину есть величина бесконечно малая, т.е., пусть А — конечное число, — бесконечно малая величина, тогда А — БМВ.
3. Произведение двух бесконечно малых величин есть величина бесконечно малая. Пусть и — БМВ, тогда — есть БМВ.
4. Предел бесконечно малой величины = 0, т.е. lim = 0.
5. Величина, обратная БМВ, есть величина бесконечно большая (ББВ),1 т.е. где В — бесконечно большая величина и наоборот:2
6. Отношение двух бесконечно малых величин неопределенно, т.е3. Зависит это отношение от того, насколько быстрее одна БМВ стремится к нулю, чем другая. Например, пусть  При n.
При n.  Бесконечно малая величина в два раза быстрее стремится к нулю, чем бесконечно малая величина .
Бесконечно малая величина в два раза быстрее стремится к нулю, чем бесконечно малая величина .
19. Теорема о пределе монотонной функции. Принцип сходимости. Критерий Коши.
Критерий монотонности функции, имеющей производную на интервале) Пусть функция  непрерывна на (a,b),и имеет в каждой точке
непрерывна на (a,b),и имеет в каждой точке  производную f'(x). Тогда
производную f'(x). Тогда
f возрастает на (a,b) тогда и только тогда, когда 
f убывает на (a,b) тогда и только тогда, когда 
Монотонные функции
Докажем теперь две теоремы, касающиеся непрерывности монотонных функций.
Теорема 1.. Пусть f(x) определена и монотонна на замкнутом отрезке [a,b]. Тогда она может иметь на этом отрезке только разрывы I рода (скачки).
Доказательство.
Пусть, для определенности, f(x) монотонно возрастает.
 Возьмем какую-то точку x0 О[a,b]. Пусть мы приближаемся к точке х0 слева (см. рис.). Тогда при этом значения функции f(x) будут монотонно возрастать. Но они будут ограничены сверху, например, величиной f(x0). Поэтому, по теореме о пределе монотонно-возрастающей функции будет существовать конечный
Возьмем какую-то точку x0 О[a,b]. Пусть мы приближаемся к точке х0 слева (см. рис.). Тогда при этом значения функции f(x) будут монотонно возрастать. Но они будут ограничены сверху, например, величиной f(x0). Поэтому, по теореме о пределе монотонно-возрастающей функции будет существовать конечный  .
.
При движении к х0 справа значения f(x) будут монотонно убывать, но будут ограничены снизу величиной f(x0). Поэтому снова существует конечный  .
.
Если f(x0+0)= f(x0-0), то f(x) будет непрерывна в точке х0, если же f(x0+0)<f(x0-0), то у f(x) в точке х0 будет разрыв I рода. <
Определение. Говорят, что значения функции f(x), определенной на <a,b>, заполняют некоторый отрезок <c,d> сплошь, если
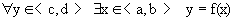 .
.
Теорема 2. Для того, чтобы монотонная функция f(x) была непрерывной на [a,b], необходимо и достаточно, чтобы ее значения заполняли отрезок [f(a), f(b)] сплошь.
Доказательство.
Пусть, для определенности, f(x) монотонно возрастает.
Пусть f(x) непрерывна на [a,b]. Тогда  . Согласно второй теореме Больцано-Коши,
. Согласно второй теореме Больцано-Коши,  . Поэтому отрезок [f(a),f(b)] заполнен сплошь.
. Поэтому отрезок [f(a),f(b)] заполнен сплошь.
Пусть f(x) не является непрерывной на [a,b]. Тогда она на [a,b] может иметь только разрывы I рода. Пусть х0 – координата такого разрыва. Возможные поведения графика f(x) изображены на рисунках.
 Из них видно, что в этом случае отрезок [f(a), f(b)] заполнен не сплошь
Из них видно, что в этом случае отрезок [f(a), f(b)] заполнен не сплошь
20. Сравнение бесконечно малых и бесконечно больших.
Отношение бесконечно малых величин образует так называемую неопределённость  .
.
Определения:Допустим, у нас есть бесконечно малые при одном и том же 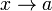 величины α(x) и β(x) (либо, что не важно для определения, бесконечно малые последовательности).
величины α(x) и β(x) (либо, что не важно для определения, бесконечно малые последовательности).
Если  , то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).
, то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).
Если  , то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).
, то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).
Если  (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.
(предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.
Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).
Если  (предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.
(предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.
Для вычисления подобных пределов удобно использовать правило Лопиталя.
21. Нахождение порядка малости и порядка роста.
Порядок малости БМ при 

 Порядок роста ББ при
Порядок роста ББ при 
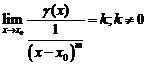
Порядок малости БМ при 
 рядок
рядок
22. Непрерывность функции одной переменной.
Функция f(х) непрерывна в тчк 
 когда
когда 
По Гейне Функция f(х) непрерывна в тчк 
 когда для любой последовательности
когда для любой последовательности  и для любого
и для любого 
По Коши 
функция в тчк x0 если БМ прирощ аргумент соотв БМ прирощ функции 

функция непрерывна на множ-ве,если она непрерывна в каждой тчке этого множ-ва
23. Односторонняя непрерывность. Точки разрыва и их классификация.
Функция непрерывна x0 слева  когда
когда  f (x0 -0)= f ( x0)
f (x0 -0)= f ( x0)
Функция непрерывна справа  когда
когда 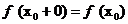
Из непрерывности справа и слева следует непрерывность и в тчке.верно и обратное.
Тчк 1-го рода если в ней существ и конечн оба односторонних предела,если пред=,то x0 тчк устранимого разрыва,если предел  односторон,то
односторон,то  наз-ся скачок функц,и разрыв неустраним.Тчк 2-го рода если хотя бы один предел =
наз-ся скачок функц,и разрыв неустраним.Тчк 2-го рода если хотя бы один предел =  или несущест.бесконечного разрыва.
или несущест.бесконечного разрыва.
24. Локальные свойства непрерывных функций.
Если 2 тчк фун f g непрерывны в тчк x0 ,где x0 принадлежитпересечению D(f) D(g),тогда  ,также не прерывны в тчк x0
,также не прерывны в тчк x0
док-ворассмотрим  т.к. f g нерперывн в тчк x0 след сущ
т.к. f g нерперывн в тчк x0 след сущ 
25. Первая теорема Больцано-Коши.
Если функция непрерывна на I и в 2 его точках a иbпринимает значения разных знаков, то по крайней мере в одной точке c между a и b функция обращается в нуль, т.е. f(c)=0
Доказательство: опирается на теорему Кантора и следствие.
Разделим отрезок [a;b] точкой 2a+b на 2 равных отрезка, если f(2a+b)=0 , то теорема доказана и с=2a+b, если же f(2a+b)/=0 , то на концах по крайней мере одного из частичных отрезков функция f принимает значения разных знаков.
Обозначим этот сегмент через [a1;b1]. Сегмент [a1;b1] разбиваем точкой c=2a1+b1на две равные части. Если f(2a1+b1)=0 , то теорема доказана и с=2a1+b1, если же f(2a1+b1)/=0 , то обозначим через [a2;b2] тот частичный сегмент на концах которого функция принимает значения разных знаков. И т.д.
Продолжив этот процесс либо при некотором k∈N будем иметь f(2ak+bk)=0 и тогда теорема доказана (здесь с=2ak+bk), либо ни при каких k∈N условие f(2ak+bk)=0 не выполнится.
При этом будет построена посл. ([an;bn]стягиванием сегментов
1)[a;b]≥[a1;b1]≥...≥[an;bn]≥...
2)limn→∞(b−nan)=2b−a=0
Поэтому существует единственная точка C содержащаяся во всех сегментах. Функция f непрерывна в точке C∈I и поскольку c=limann→∞=limbnn→∞, то в любой окрестности точки C функция f принимает значения разных знаков. По следствиюf(c)=0. ч.т.д.
26. Вторая теорема Больцано-Коши.
о промежуточных значениях непрерывной функции в математическом анализе и общей топологии — это утверждение о том, что если непрерывная функция принимает два значения, то она принимает и любое значение между ними
Рассмотрим функцию  Она непрерывна на отрезке
Она непрерывна на отрезке  и
и  ,
,  Покажем, что существует такая точка
Покажем, что существует такая точка  , что
, что  Разделим отрезок
Разделим отрезок  точкой
точкой  на два равных по длине отрезка, тогда либо
на два равных по длине отрезка, тогда либо  и нужная точка
и нужная точка  найдена, либо
найдена, либо 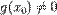 и тогда на концах одного из полученных промежутков функция
и тогда на концах одного из полученных промежутков функция  принимает значения разных знаков(на левом конце меньше нуля, на правом больше).
принимает значения разных знаков(на левом конце меньше нуля, на правом больше).
Обозначив полученный отрезок  , разделим его снова на два равных по длине отрезка и т.д. Тогда, либо через конечное число шагов придем к искомой точке
, разделим его снова на два равных по длине отрезка и т.д. Тогда, либо через конечное число шагов придем к искомой точке  , либо получим последовательность вложенных отрезков
, либо получим последовательность вложенных отрезков  по длине стремящихся к нулю и таких, что
по длине стремящихся к нулю и таких, что 
Пусть  - общая точка всех отрезков
- общая точка всех отрезков  ,
,  Тогда c = lim an = lim bn, и в силу непрерывности функции
Тогда c = lim an = lim bn, и в силу непрерывности функции 
g(c) = lim g(an) = lim g(bn).

Поскольку 
получим, что
27. Первая теорема Вейерштрасса.
Если функция непрерывна на сегменте, то она ограничена на нем.
Доказательство: методом от противного, воспользуемся свойством замкнутости сегмента [a;b]. Из любой последовательности (xn) этого сегмента можем выделить подпоследовательность xnk, сходящуюся к x0∈[a;b].
Пусть f не ограничена на сегменте [a;b], например, сверху, тогда для всякого натуральногоn∈Nнайдется точка xn∈[a;b], что f(xn)>n. Придавая n значения 1,2,3,{\ldots}, мы получим последовательность (xn) точек сегмента [a;b], для которых выполнено свойствоf(x1)>1,f(x2)>2,f(x3)>3,...,f(xn)>n...
Последовательность (xn) ограничена и поэтому из нее по теореме можно выделить подпоследовательность(xnk), которая сходится к точке x0∈[a;b]: limk→∞xnk=x0 (1)
Рассмотрим соответствующую последовательность (f(xnk)). С одной стороны f(xnk)>nk и поэтомуlimk→∞f(xnk)=+∞ (2),
С другой стороны, учитывая определение непрерывной функции по Гейне из (1) будем иметьlimk→∞f(xnk)=f(x0) (3)
Получаем равенства (2) и (3) противоречат теореме (о единственности предела). Это противоречие и доказывает справедливость теоремы. Аналогично доказывается ограниченность функции снизу.
28. Вторая теорема Вейерштрасса.
Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения).
Доказательство: Пусть f(x)∈C([a;b]), c=infx∈[a;b]f(x), d=supx∈[a;b]f(x). По первой
теореме Вейерштрасса c,d∈R. Докажем, что f достигает на [a;b] своих граней, т.е. найдутся такие точкиx1,x2∈[a;b], чтоf(x1)=c,f(x2)=d.
Докажем, например, существование точки x2.
По определению верхней грани имеем (∀x∈[a;b])(f(x)=d). Предположим противное, т.е. точки x2, в которой f(x2)=dна [a;b], тогда на [a;b] выполняется условиеf(x)<d или d−f(x)>0. Далее введем вспомогательную функцию ϕ(x)=1d−f(x) . ϕ(x) на [a;b] положительна и непрерывна (как отношение двух непрерывных на [a;b] функций и d−f(x)/=0) , поэтому по первой Т. Вейерштрасса ϕ(x) на [a;b] ограничена.
Это означает, что при некотором М>0 (∀x∈[a;b])(0<1d−f(x)≤M), отсюда имеем f(x)≤d−1M<d.
Полученное неравенство противоречит тому, что d является верхней гранью функции f(x) на [a;b], т.е. наименьшим из верхних границ. Полученное противоречие и означает существование точки x2 такой, чтоf(x2)=d.
Аналогично доказывается существование точки x1∈[a;b], такой что f(x1)=c.
29. Непрерывность обратной функции.
Пусть функция y=f(x), заданная на множестве X, обратима. Это значит, что функция f различным значениям аргумента ставит в соответствие различные значения функции, т.е. для любых x1,x2∈X: x1/=x2⇒f(x1)/=f(x2).
В этом случае для каждого y∈Y=f(X) существует один и только один элемент x∈Xтакой, что y=f(x). А это означает, что на множестве Y определена функция g:Y→X, которую и называют обратной функцией к функции y=f(x) и обозначают: x=f−1(y). При этом очевидно, что функция f являетсяобратной к функции f−1.Поэтомуфункции y=f(x) и x=f−1(y) называют взаимно обратными.  Т.о., если функция f:X→Y, где Y=f(X), обратима, то для нее существует единственная обратная функция f−1:Y→X и если y=f(x) то x=f−1(y), и если x=f−1(y), то y=f(x) и f−1(f(x))=x при любомx∈X, f−1(f(y))=y при любом y∈Y.
Т.о., если функция f:X→Y, где Y=f(X), обратима, то для нее существует единственная обратная функция f−1:Y→X и если y=f(x) то x=f−1(y), и если x=f−1(y), то y=f(x) и f−1(f(x))=x при любомx∈X, f−1(f(y))=y при любом y∈Y.
Теорема 1. Если функция y=f(x) строго возрастает (убывает) на множестве X, то для нее существуетобратная функция x=f−1(y), которая определена на множестве Y=f(X) и является на Y строго возрастающей (убывающей).
Доказательство. По условию функция f строго возрастает на множестве X. Это значит для любыхx1,x2  Xи x1<x2 следует f(x1)<f(x2). Отсюда следует, что функция f обратима на X, следовательно, для нее существует обратная функция f−1:Y→X. Покажем, что функция f−1 строго возрастает на множестве Y. Пусть y1 и y2- любые точки из Y и y1<y2. Докажем, что x1=f−1(y1)<x2=f−1(y2). Допустим, чтоx1≥x2. По условию функция f строго возрастает на X, поэтому из условия x1≥x2вытекает неравенствоy1=f(x1)≥y2=f(x2), что противоречит условию y1<y2.
Xи x1<x2 следует f(x1)<f(x2). Отсюда следует, что функция f обратима на X, следовательно, для нее существует обратная функция f−1:Y→X. Покажем, что функция f−1 строго возрастает на множестве Y. Пусть y1 и y2- любые точки из Y и y1<y2. Докажем, что x1=f−1(y1)<x2=f−1(y2). Допустим, чтоx1≥x2. По условию функция f строго возрастает на X, поэтому из условия x1≥x2вытекает неравенствоy1=f(x1)≥y2=f(x2), что противоречит условию y1<y2.
Т.о., условие строгой монотонности функции является достаточным для существования обратной функции.
30. Равномерная непрерывность функции.
31. Теорема Кантора. Модуль непрерывности.
32. Понятие производной. Геометрический и физический смысл.

 ,рассмотрим
,рассмотрим  ,если сущ конечн предел при дельта y=0,он наз-ся производ в тчк х0,геометрич смысл-касательная и нормаль к графику,физическ-мгновен скорость
,если сущ конечн предел при дельта y=0,он наз-ся производ в тчк х0,геометрич смысл-касательная и нормаль к графику,физическ-мгновен скорость
33. Дифференцируемость функции одной переменной.
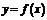 назыв дифир на пром a,b
назыв дифир на пром a,b  когда ее прирощение допус прирощен
когда ее прирощение допус прирощен  А-const;
А-const;  -БМФ при
-БМФ при  , теорема 1 связь между дифф и непрерыв-тью,если fx- дифф в тчк х0… док-во. функция дифф
, теорема 1 связь между дифф и непрерыв-тью,если fx- дифф в тчк х0… док-во. функция дифф  f непрер в тчк х0,у=|х|- непрерыв,но не дифф в нуле
f непрер в тчк х0,у=|х|- непрерыв,но не дифф в нуле
34. Критерий дифференцируемое™ функции в точке.
Функция дифф в тчк х0  ,когда сущ произв в тчк х0
,когда сущ произв в тчк х0  R
R
Док-во: Необход дифф функ,док что сущ произв 
 делим обе части на
делим обе части на 
 и перейд к пределу
и перейд к пределу 



35. Дифференциал функции. Геометрический смысл. Инвариантность формы первого дифференциала.
Диф фун в тчк-главнвя линейная относительно  ,часть прирощ фун-ции
,часть прирощ фун-ции  или
или  ,
,  -прирощ зав перем,
-прирощ зав перем,  -прирощ независ перем,
-прирощ независ перем,  -диффер независ перем,
-диффер независ перем,  =
= 

Геометр смысл прирощение ординаты касательной.
Инвар формы первого дифф. Вид (форма 1-го диф не зависит от того является ли х зависим или не зависим,отличие в том когда х –не завис переем,то в рав-ве (1)  ;
;  -прирощ,а когда х зависим,
-прирощ,а когда х зависим,  ,то в (1)
,то в (1) 
36. Дифференцирование сложной и обратной функций.

 Сожной--
Сожной--  -диф в тчк х0,а
-диф в тчк х0,а  +
+  ,причем
,причем  ,тогда
,тогда  -диф в тчк t0 причем
-диф в тчк t0 причем  ;
; 
Обратной-- Производная от взаимно обратных функций обратны по величине: или .
Примеры.
№1. 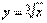 . Здесь
. Здесь  и
и  .
. 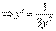 . Выразим теперь производную
. Выразим теперь производную  через независимую переменную x. Для этого подставим в полученное равенство вместо y его значение
через независимую переменную x. Для этого подставим в полученное равенство вместо y его значение  .
.
Теперь продифференцируем функцию по общей формуле:  Получился тот же результат.
Получился тот же результат.
37. Дифференцирование алгебраической суммы, произведения и частного.
38. Нахождение производных простейших элементарных функций.
39. Производные и дифференциалы высших порядков.
40. Формула Лейбница. Пример.
41. Теорема Ферма.
42. Теорема Ролля.
Пусть функция f:
1) Непрерывна на отрезке [a,b];
2) Имеет в каждой точке интервала (a,b) конечную или определенного знака бесконечную производную;
3) Принимает равные значения на концах отрезка, т.е f(a)= f(b)
Тогда существует хотя бы одна такая точка  (a,b), в которой f’(
(a,b), в которой f’(  )=0
)=0
Геометрический смысл
Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс

Доказательство
Т.к функция f(x) непрырывна на [a,b], то по свойству непрерывных функций она достигает на этом отрезке максимальное значение М и минимальное значение m.
Возможны два случая: максимум и минимум достигаются на концах отрезка или что-либо (или максимум, или минимум) попадает вовнутрь интервала. 1)В первом случае f(x)=const=M=m. Поэтому производная равна нулю f’(  )= 0 в любой точке отрезка [a,b], и теорема доказана. 2)Во втором случае, т.к f(x) дифференцируема в точке
)= 0 в любой точке отрезка [a,b], и теорема доказана. 2)Во втором случае, т.к f(x) дифференцируема в точке  , из теоремы Ферма следует, что f’(
, из теоремы Ферма следует, что f’(  )=0.
)=0.
т. 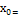 f’(
f’(  =0
=0
43. Теорема Лагранжа.
Пусть функция f(x) непрерывна на отрезке [a,b], и дифференцируема на (а,b), она имеет конечную или определенного знака бесконечную производную, то в этом интервале существует по крайней мере одна такая точка. 
f’(  )=
)=  ,tg
,tg 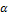 = f’(
= f’(  ), tg
), tg 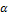 =
= 
Геометрический смысл теоремы Лагранжа

Доказательство.Рассмотрим
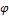 (x)=f(x)-f(a)-
(x)=f(x)-f(a)-  (x-a),
(x-a),  ,
,  (a-a)=0
(a-a)=0
 (
(b-a)=0,По Теореме Ролля существует т. 

 f’(
f’(  -
-  =0,f’(
=0,f’(  =
= 
44. Теорема Коши.
45. Формула Тейлора.

изображающая функцию f (x), имеющую n-ю производную  (a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена
(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена 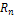 (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем
(x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем  [то есть
[то есть
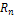 (x) = an (x)
(x) = an (x)  , где an (x) → 0 при х → а]. Если в интервале между а и х существует (n + 1)-я производная, то
, где an (x) → 0 при х → а]. Если в интервале между а и х существует (n + 1)-я производная, то 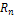 (x) можно представить в видах:
(x) можно представить в видах:

где ξ и  — какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а Соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений.
— какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а Соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений.
46. Правило Лопиталя.
Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть  или
или  . Тогда, если существует предел отношения производных этих функций
. Тогда, если существует предел отношения производных этих функций  , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
(1)  Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
47. Условие постоянства функции.
48. Условие монотонности функции.
Условия монотонности функции.Условие (нестрогой) монотонности функции на интервале. Пусть функция  имеет производную в каждой точке интервала
имеет производную в каждой точке интервала  . Для того, чтобы эта функция была монотонно возрастающей на интервале
. Для того, чтобы эта функция была монотонно возрастающей на интервале  , необходимо и достаточно выполнение условия
, необходимо и достаточно выполнение условия  для
для  . Для того, чтобы функция
. Для того, чтобы функция  была монотонно убывающей на интервале
была монотонно убывающей на интервале  , необходимо и достаточно выполнение условия
, необходимо и достаточно выполнение условия  для
для  .Док-во. Необходимость. Если f(x) монотонно возрастает, то для любых
.Док-во. Необходимость. Если f(x) монотонно возрастает, то для любых 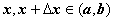 , при
, при  выполняется
выполняется 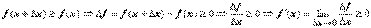
49. Необходимое условие экстремума.
Необходимое условие экстремума Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f (xо) = 0, либо f (xо) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
50. Первое достаточное условие экстремума.
Первое достаточное условие. Пусть xо - критическая точка. Если f (x) при переходе через точку xо меняет знак плюс на минус, то в точкеxо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет
51. Второе и третье достаточное условие экстремума.
Пусть функция f(x) имеет производную
f (x) в окрестности точки xо и вторую производную  в самой точке xо. Если f (xо) = 0,
в самой точке xо. Если f (xо) = 0,  >0 (
>0 (  <0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же
<0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же  =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
52. Экстремум функции не дифференцируемой в данной точке.
Теорема. Пусть функция у=f(x).
1) дифференцируема всюду в некоторой окрестности точки С, за исключением, быть может, самой точки С;
2) непрерывна в точке С.
Тогда, если существует окрестность точки С, в пределах которой производная положительна (отрицательна) слева от точки С и отрицательна (положительна) справа от точки С, то функция f(x) имеет в точке С локальный максимум (минимум). Если же производная ()xf′()xf′ имеет один и тот же знак слева и справа от точки С, то экстремума в точке С нет.
Замечание. Требование 2) непрерывности функции в точке С существенно, ибо отсутствие этого требования может привести к функциям, не имеющим экстремума в т. С
53. Направление выпуклости и вогнутости графика функций. Точки перегиба.
Точки перегиба графика функции
Предположим, что график функции y=f(x) имеет определенное направление выпуклости на каждом из интервалов (а,с) и (с,b), где числа а,b,c связаны неравенствами a<c<b. Предположим, что к графику функции y=f(x) в точке М(с,f(c)) cуществует касательная не параллельная оси OY, тогда точка М(с,f(c)) графика функции y=f(x) называется точкой перегиба этого графика, если существует такая окрестность точки С оси абсцисс, в пределах которой график функции y=f(x) слева и справа от точки С имеет разные направления выпуклости.
Точка перегиба функции  внутренняя точка x0 области определения f, такая что f непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и x0 является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.
внутренняя точка x0 области определения f, такая что f непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и x0 является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.
54. Необходимое условие перегиба.




пусть 


 - т. локального макс.
- т. локального макс.
пусть 



 - т. локального мин
- т. локального мин
55. Первое достаточное условие перегиба.
Первое достаточное условие существования точки перегиба: если функция f(x) в некоторой окрестности точки x k раз непрерывно дифференцируема, причем k нечётно и  , и
, и  при
при  , а
, а  , то функция f(x) имеет в x0 точку перегиба
, то функция f(x) имеет в x0 точку перегиба
56. Второе достаточное условие перегиба.
Второе достаточное условие существования точки перегиба: Если в некоторой точке вторая производная функции равна нулю, а третья не равна нулю, то эта точка является точкой перегиба
57. Третье достаточное условие перегиба.
Третье достаточное условие перегиба-Пусть  , тогда если n-чётное число,то
, тогда если n-чётное число,то  - является абсциссой точки перегиба графика функции y=f(x).
- является абсциссой точки перегиба графика функции y=f(x).
58. Асимптоты графика функций.
Аси́мпто́та- прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. Прямая x = a называется вертикальной асимптотой графика функции f (x) при x → a, если выполнено хотя бы одно из условий  ,
, 
Прямая y = b называется горизонтальной асимптотой графика функции f (x) при x → +∞, если 
Прямая y = kx + b, k ≠ 0 называется наклонной асимптотой графика функции f (x) при x → +∞, если  Аналогично определяются горизонтальная и наклонная асимптоты при x → –∞.
Аналогично определяются горизонтальная и наклонная асимптоты при x → –∞.
59. Краевой экстремум.
60. Первообразная функции. Неопределенный интеграл.
называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Так, например, функция  является первообразной
является первообразной  . Так как производная константы равна нулю,
. Так как производная константы равна нулю,  будет иметь бесконечное количество первообразных; таких как
будет иметь бесконечное количество первообразных; таких как  или
или  … и т. д.; таким образом семейство первообразных функции x2 можно обозначить как F(x) = x3 / 3 + C, где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.
… и т. д.; таким образом семейство первообразных функции x2 можно обозначить как F(x) = x3 / 3 + C, где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.
Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:
 Это соотношение называется формулой Ньютона — Лейбница.
Это соотношение называется формулой Ньютона — Лейбница.
Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов: 
Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.
Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом: 
Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации)
Неопределённый интегра́л для функции  — это совокупность всех первообразных данной функции.
— это совокупность всех первообразных данной функции.
Если функция  определена и непрерывна на промежутке
определена и непрерывна на промежутке  и
и  — её первообразная, то есть
— её первообразная, то есть  при
при  , то
, то 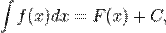
 ,
,
где С — произвольная постоянная.
 ,
,  ,
,  ,
,
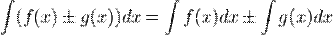 ,Если
,Если  , то и
, то и  , где u = φ(x) — произвольная функция, имеющая непрерывную производную.
, где u = φ(x) — произвольная функция, имеющая непрерывную производную.
61. Интегрирование с помощью замены переменной. Интегрирование по частям.
один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы
для неопределённого интеграла: 
для определённого: 
Предполагается, что нахождение интеграла  проще, чем
проще, чем  . В противном случае применение метода не оправданно.Получение формулдля неопределённого интеграла
. В противном случае применение метода не оправданно.Получение формулдля неопределённого интеграла
Функции  и
и  гладкие, следовательно, возможно дифференцирование:
гладкие, следовательно, возможно дифференцирование: 
Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства: 
Операция интегрирования обратна дифференцированию: 
После перестановок: 
Не стоит, однако, забывать, что это равенство подразумевается в смысле равенства множеств, то есть, грубо говоря, с точностью до константы, возникающей во время интегрирования.
62. Интегрирование рациональных функций.
Любую рациональную функцию можно представить в виде  где S, P, Q - многочлены, степень P < степени Q.
где S, P, Q - многочлены, степень P < степени Q.
После разложения P(x)/Q(x) на элементарные дроби интегрирование рациональной функции сводится к интегрированию простейших рациональных функций.
Метод Остроградского выделения рациональной части интеграла от рациональной функции
Если P(x)/Q(x) - правильная дробь, то 
где  - многочлены, степень
- многочлены, степень  степени
степени  степень
степень  степени
степени  Если
Если  то
то 

Метод рационализации
(R - рациональная функция двух переменных)
63. Интегрирование дробно-линейных иррациональностей.
Интегрирование иррациональностей от дробно-линейной функции
 рационализирует подстановка
рационализирует подстановка 
64. Разложение правильной рациональной дроби на сумму простейших.
Пусть знаменатель правильной рациональной дроби  может быть представлен в виде
может быть представлен в виде  (множителей вида
(множителей вида  может быть несколько), где — a1, … , al, b, q, p заданные числа
может быть несколько), где — a1, … , al, b, q, p заданные числа  .
.
k  , трехчлен
, трехчлен  не имеет действительных корней.
не имеет действительных корней.
Тогда  представляется в виде суммы простейших дробей 1—3 типов:
представляется в виде суммы простейших дробей 1—3 типов:

Где  — неизвестные коэффициенты, которые находятся путем приведения суммы справа к общему знаменателю и последующего приравнивания полученного числителя к
— неизвестные коэффициенты, которые находятся путем приведения суммы справа к общему знаменателю и последующего приравнивания полученного числителя к 
65. Интегрирование дифференциальных биномов.
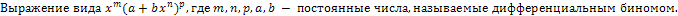


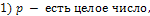

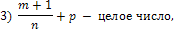




66. Интегрирование выражений, содержащих тригонометрические функции.

1) Подстановка sinx=t, если n – целое положительное нечетное число;
2) Подстановка cosx=, если m – целое положительное четное число;
3) формулы понижения порядка  x=
x=  x=
x= 
 , если m и n - целые неотрицательные четные числа.
, если m и n - целые неотрицательные четные числа.
4) Подстановка tgx=t, если m+n – есть четное отрицательное целое число.
67. Определенный интеграл Римана. Геометрический смысл.
68. Верхние и нижние суммы Дарбу. Свойства сумм. Интегралы Дарбу. Лемма Дарбу.
69. Классы интегрируемых функций.
70. Свойства определенного интеграла.
Пусть f(x), g(x), [a;b] c- const
1) 
2) 
3)  (a
(a 
4) 
5) 
6) 
71. Оценки интегралов.
1. Если 
2. 
3. Если  .
.
72. Первая теорема о среднем.
Если функция f ( x) непрерывна на отрезке [a,b],то найдётся такая точка ξ  [a,b], что справедливо равенство
[a,b], что справедливо равенство
 называемое формулой среднего значения.
называемое формулой среднего значения.
Величина  называется средним значением функции f(x) на отрезке [a,b].
называется средним значением функции f(x) на отрезке [a,b].
73. Вторая теорема о среднем.
Если f, g непрерывны, а g не меняет знак, то

Формула Бонне
 (g монотонна)
(g монотонна)
74. Первообразная непрерывной функции.
75. Формула Ньютона-Лейбница.
Если функция f (x) интегрируема на [a; b], то для любого x  существует интеграл
существует интеграл
 который называется интегралом с переменным верхним пределом.
который называется интегралом с переменным верхним пределом.
Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.
Если функция f интегрируема на [a; b] и непрерывна в 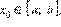 то функция F (x) дифференцируема в
то функция F (x) дифференцируема в  причем
причем  Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида
Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида  где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда  Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).
Пусть f (x) непрерывна на [a; b], g (t) имеет непрерывную производную на [α; β],  Тогда если a = g (α), b = g (β), то справедлива формула замены переменной в определенном интеграле:
Тогда если a = g (α), b = g (β), то справедлива формула замены переменной в определенном интеграле:  Если функции u (x) и v (x) имеют на [a;
Если функции u (x) и v (x) имеют на [a;  ], непрерывные производные, то справедлива формула интегрирования по частям:
], непрерывные производные, то справедлива формула интегрирования по частям:

76. Интегрирование по частям в определенном интеграле. Интегрирование с помощью замены переменной.
Теорема. Если функции u(x) и v(x) непрерывно дифференцируемы на отрезке [a,b], то
 (1)
(1)
Эта формула называется формулой по частям для определённого интеграла.
Доказательство. Имеем
 (2)
(2)
Все написанные интегралы существуют, ибо подынтегральные функции непрерывны. Согласно формуле Ньютона-Лейбница (  ), имеем
), имеем
 (3)
(3)
Сравнив формулы 2 и 3, получим равенство
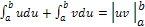 (4)
(4)
Откуда и следует формула 1.
Теорема. Пусть: 1)функция f(x) непрерывна на интервале (a,b);
2)функция φ(t) определена и непрерывна вместе со своей производной φ’(t) на интервале (α,β), причём для всех t є (α,β) выполняется неравенство a< φ(t)<b .
Тогда если α0 є (α,β), β0 є (α,β), α0= φ (α0), β0 = φ (β0), то
 (1)
(1)
Эта формула называется формулой замены переменной в определённом интеграле или формулой интегрирования подстановкой.
Доказательство. Пусть F(x)- какая-либо первообразная функция f(x)на интервале (a,b). Тогда для точек t интервала (α,β) имеет смысл сложная функция F[φ (t)], которая является первообразной для функции f[φ (t)] φ’(t). По формуле Ньютона –Лейбница 

Из этих равенств и следует формула (1).
77. Несобственные интегралы первого рода.
Пусть f(x) определена и непрерывна на промежутке  и
и  . Тогда:
. Тогда:
1)Если  , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае
 называется сходящимся.
называется сходящимся.
2)Если не существует конечного  , то интеграл
, то интеграл  называется расходящимся к
называется расходящимся к  , или просто расходящимся.
, или просто расходящимся.
Пусть f(x) определена и непрерывна на множестве промежутке  и
и  . Тогда:
. Тогда:
1)Если 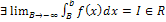 , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае  называется сходящимся.
называется сходящимся.
2)Если не существует конечного  , то интеграл
, то интеграл  называется расходящимся к
называется расходящимся к  , или просто расходящимся.
, или просто расходящимся.
Если функция f(x) определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:  , где с — произвольное число.
, где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции
78. Признаки сравнения.
Теорема. Пусть функции f и g неотрицательны на полуинтервале [a,b) и
 (1). Тогда:
(1). Тогда:
-Если интеграл  сходится, то сходится и интеграл
сходится, то сходится и интеграл 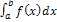
-Если интеграл  расходится, то расходится и интеграл
расходится, то расходится и интеграл 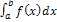
Доказательство. Пусть интеграл  сходится. Из условия (1) следует существование такого
сходится. Из условия (1) следует существование такого  , и такого c > 0 , что для всех
, и такого c > 0 , что для всех  выполняется неравенство
выполняется неравенство  (2).
(2).
Из сходимости интеграла  следует и сходимость интеграла
следует и сходимость интеграла  . В силу же необходимости условий леммы для сходимости интеграла, существует такое число М>0, что для любого
. В силу же необходимости условий леммы для сходимости интеграла, существует такое число М>0, что для любого  справедливо неравенство
справедливо неравенство  . Отсюда и из неравенства (2) имеем
. Отсюда и из неравенства (2) имеем
 .
.
Из этого неравенства, в силу достаточности условий леммы для сходимости интеграла от неотрицательной функции, получаем, что интеграл  , следовательно, и интеграл
, следовательно, и интеграл 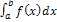 сходятся.
сходятся.
Первое утверждение теоремы доказано. Второе доказывается аналогично.
79. Абсолютная и условная сходимость несобственных интегралов. Признак Абеля-Дирихле.
Определение 1. Несобственный интеграл  называется абсолютно сходящимся, если сходится
называется абсолютно сходящимся, если сходится  .
.
Определение 2.Несобственный интеграл  называется условно сходящимся, если
называется условно сходящимся, если  сходится, а
сходится, а  расходится.
расходится.
Признак Дирихле.
Пусть : 1) функция f непрерывна и имеет ограниченную первообразную F при  ;
;
2)функция g непрерывно дифференцируема и убывает при  ;
;
3)  .
.
Тогда сходится интеграл  . (1)
. (1)
Доказательство. Прежде всего заметим, что, в силу сделанных предположений, функция fg непрерывна, а значит, и интегрируема по Риману на любом отрезке  , и поэтому имеет смысл говорить о несобственном интеграле (1).
, и поэтому имеет смысл говорить о несобственном интеграле (1).
Проинтегрировав по частям произведение  на отрезке
на отрезке  получим
получим  . (2)
. (2)
Исследуем поведение обоих слагаемых правой части при  . В силу ограниченности функции F
. В силу ограниченности функции F  .
.
Из условий 2 и 3 теоремы следует, что функция g не отрицательна для всех  , в частности
, в частности  ; поэтому
; поэтому  .
.
Кроме того, в силу условия 3,  , и следовательно,
, и следовательно,
 .
.
Далее, из убывания функции g следует, что  при
при  , поэтому
, поэтому
 , так как
, так как  .
.
Таким образом, интегралы  ограничены в совокупности при всех b > a , поэтому интеграл
ограничены в совокупности при всех b > a , поэтому интеграл  абсолютно сходится, т.е. существует конечный предел
абсолютно сходится, т.е. существует конечный предел  .
.
Признак Абеля.
Теорема. Если на полуоси  : 1)функция f непрерывна и сходиться интеграл
: 1)функция f непрерывна и сходиться интеграл  (1);
(1);
2)функция g непрерывно дифференцируема, ограничена и монотонна, то интеграл  сходится.
сходится.
Доказательство. Покажем, что эта теорема вытекает из предыдущей. Прежде всего отметим, что интегралы  и
и  сходятся или расходятся одновременно и что, в силу монотонности функции g, одна из функций g или –g убывает.
сходятся или расходятся одновременно и что, в силу монотонности функции g, одна из функций g или –g убывает.
Пусть, для определенности убывает функция g. В силу её ограниченности и монотонности, существует конечный предел  , а так как функция g убывает, то при
, а так как функция g убывает, то при 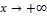 , убывая, стремиться к нулю и разность
, убывая, стремиться к нулю и разность  .
.
Представим произведение  в виде
в виде  . (2)
. (2)
В силу сходимости интеграла (1), интеграл  также сходится. Из этого следует, что интегралы
также сходится. Из этого следует, что интегралы  ,
,  , ограничены В самом деле, из существования конечного предела
, ограничены В самом деле, из существования конечного предела 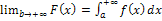 следует ограниченность функции F в некоторой окрестности
следует ограниченность функции F в некоторой окрестности  бесконечно удалённой точки
бесконечно удалённой точки  . На отрезке же
. На отрезке же  функция F ограничена, ибо она непрерывна. В результате функция F ограничена на всей полупрямой
функция F ограничена, ибо она непрерывна. В результате функция F ограничена на всей полупрямой  . Функция F является первообразной функции f; тем самым функция f имеет ограниченную первообразную при
. Функция F является первообразной функции f; тем самым функция f имеет ограниченную первообразную при  .
.
Таким образом, для интеграла  выполнены все условия признака Дирихле, поэтому этот интеграл сходиться. В силу доказанного, из равенства (2) следует сходимость интеграла
выполнены все условия признака Дирихле, поэтому этот интеграл сходиться. В силу доказанного, из равенства (2) следует сходимость интеграла  .
.
80. Несобственные интегралы второго рода.
Пусть f(x) определена на  и
и  . Тогда: Если
. Тогда: Если
 , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана второго рода. В этом случае
и интеграл называется несобственным интегралом Римана второго рода. В этом случае
 называется сходящимся.
называется сходящимся.
2)Если 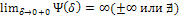 , то обозначение сохраняется, а
, то обозначение сохраняется, а  называется расходящимся к
называется расходящимся к  , или просто расходящимся.
, или просто расходящимся.
Пусть f(x) определена на промежутке  , и имеет бесконечный разрыв при x=b и
, и имеет бесконечный разрыв при x=b и  . Тогда:
. Тогда:
1)Если  , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл
 называется сходящимся.
называется сходящимся.
2)Если  , то обозначение сохраняется, а
, то обозначение сохраняется, а  называется расходящимся к
называется расходящимся к  , или просто расходящимся.
, или просто расходящимся.
Если функция f(x) имеет разрыв во внутренней точке c отрезка  , то несобственный интеграл второго рода, определяется формулой:
, то несобственный интеграл второго рода, определяется формулой:  .
.
Геометрический смысл несобственного интеграла II рода
Несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции.
81. Площадь в прямоугольной системе координат и в параметрической форме.
Площадь криволинейной трапеции, расположенной «выше» оси абсцисс  , равна соответствующему определенному интегралу:
, равна соответствующему определенному интегралу:  или
или  (1)
(1)
Пусть криволинейная трапеция ограничена линиями  .
.
Для нахождения площади этой трапеции проделаем следующие операции:
1) Возьмём произвольное  и будем считать, что
и будем считать, что  .
.
2) Дадим аргументу х приращение  . Функция
. Функция  получит приращение
получит приращение  , представляющее собой площадь «элементарной криволинейной трапеции». Дифференциал площади dS есть главная часть приращения
, представляющее собой площадь «элементарной криволинейной трапеции». Дифференциал площади dS есть главная часть приращения  при
при  , и, очевидно, он равен площади прямоугольника с основанием dx и высотой у:
, и, очевидно, он равен площади прямоугольника с основанием dx и высотой у: 
3) Интегрируя полученное равенство в пределах от  , получаем
, получаем
 .
.
Отметим, что если криволинейная трапеция расположена «ниже» оси 
То её площадь может быть найдена по формуле  .
.
Формула для трапеции ограниченной кривой, заданной параметрически
 Прямыми
Прямыми  и осью Ох , то площадь её находиться по формуле
и осью Ох , то площадь её находиться по формуле

82. Площадь в полярной системе координат.
Найдём площадь криволинейного сектора, т.е. плоской фигуры, ограниченной непрерывной линией  и двумя лучами
и двумя лучами  где
где  - полярные координаты.
- полярные координаты.
1) Будем считать часть искомой площади как функцию угла 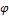 , т.е.
, т.е.
 .
.
2) Если текущий полярный угол 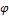 получит приращение
получит приращение  , то приращение площади
, то приращение площади  равно площади «элементарного криволинейного сектора.
равно площади «элементарного криволинейного сектора.
Дифференциал dS представляет собой главную часть приращения  при
при  и равен площади кругового сектора радиуса r с центральным углом
и равен площади кругового сектора радиуса r с центральным углом  .
.
Поэтому  .
.
Интегрируя полученное равенство в пределах  получим искомую площадь
получим искомую площадь  .
.
83. Длина дуги кривой в прямоугольной системе координат.
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии. Вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена её стремится к нулю.
Покажем, что если функция y=f(x) и её производная y’=f’(x) непрерывны на отрезке [a,b], то кривая АВ имеет длину, равную 
1) Точками  разобьём отрезок [a,b] на n частей. Пусть этим точкам соответствуют точки
разобьём отрезок [a,b] на n частей. Пусть этим точкам соответствуют точки  на отрезке кривой АВ. Проведём хорды М0М1, М1 М2,…,Мn-1Мn, длины которых обозначим соответственно через
на отрезке кривой АВ. Проведём хорды М0М1, М1 М2,…,Мn-1Мn, длины которых обозначим соответственно через  . Получим ломаную М0 М1 М2 …Мn-1 Мn , длина которой равна
. Получим ломаную М0 М1 М2 …Мn-1 Мn , длина которой равна
 .
.
2) Длину хорды  можно найти по теореме Пифагора из треугольника с катетами
можно найти по теореме Пифагора из треугольника с катетами  :
:  , где
, где  =
=  -
-  ,
,  =
= 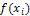 –
–  . По теореме Лагранжа о конечном прекращении функции
. По теореме Лагранжа о конечном прекращении функции  =
=  , где
, где  . Поэтому
. Поэтому 
А длина всей ломаной 
 …
…  равна
равна
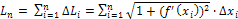 (1)
(1)
3) Длина  кривой АВ , по определению, равна
кривой АВ , по определению, равна  . Заметим, что при
. Заметим, что при  также и
также и  и, следовательно,
и, следовательно,  . Функция
. Функция  непрерывна на отрезке
непрерывна на отрезке  , так как, по условию, непрерывна функция
, так как, по условию, непрерывна функция  . Следовательно, существует предел интегральной суммы (1), когда max
. Следовательно, существует предел интегральной суммы (1), когда max 
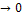 :
:

84. Дифференциал дуги в прямоугольной системе координат.
Вычисление длины дуги может быть основано на применении метода дифференциала.
1) Возьмём произвольное значение x  и рассмотрим переменный отрезок
и рассмотрим переменный отрезок  . На нём величина
. На нём величина  становится функцией от x, т.е.
становится функцией от x, т.е.  =
=  (x)(
(x)(  (a) = 0 и
(a) = 0 и  (b) =
(b) =  ).
).
2) Находим дифференциал dl функции  =
=  (x) при изменении х на малую величину
(x) при изменении х на малую величину  . Найдём
. Найдём  , заменяя бесконечно малую дугу
, заменяя бесконечно малую дугу  хордой
хордой  , стягивающей эту дугу
, стягивающей эту дугу 
Стало быть, 
3) Интегрируя 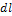 в пределах от a до b, получаем
в пределах от a до b, получаем
Равенство  называется формулой дифференциала дугив прямоугольных координатах.
называется формулой дифференциала дугив прямоугольных координатах.
Так как  , то
, то 
85. Длина дуги в параметрической форме.
Если уравнение кривой АВ задано в параметрической форме 
где x(t) и y(t) – непрерывные функции с непрерывными производными и  ,
,  то длина
то длина  кривой АВ находится по формуле
кривой АВ находится по формуле 
86. Длина дуги в полярной системе координат.
Пусть кривая АВ задана уравнением в полярных координатах  Предположим, что
Предположим, что  и
и  непрерывны на отрезке
непрерывны на отрезке  .
.
Если в равенствах  , связывающих полярные и декартовы координаты, параметром считать угол
, связывающих полярные и декартовы координаты, параметром считать угол 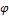 , то кривую АВ можно задать параметрически
, то кривую АВ можно задать параметрически  Тогда
Тогда 
Поэтому 
Применяя формулу  получаем
получаем 
87. Нахождение объема тела по известным площадям поперечных сечений.
Пусть потребуется найти объём  , причём известны площади
, причём известны площади  сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси
сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси 
1) Через произвольную точку  проведём плоскость П, перпендикулярную оси Ох. Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении х. Через v(x) обозначим объём части тела, лежащее левее плоскости П. Будем считать, что на отрезке [a,x] величина v есть
проведём плоскость П, перпендикулярную оси Ох. Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении х. Через v(x) обозначим объём части тела, лежащее левее плоскости П. Будем считать, что на отрезке [a,x] величина v есть
функция от x, т.е. v=v(x) (v(a)=0, v(b)=V)
2) Находим дифференциал dV функции v=v(x). Он предоставляет собой «элементарный слой» тела, заключённый между параллельными плоскостями, пересекающими ось Ох в точках  , который приближенно может быть принят за цилиндр с основанием S(x) и высотой dx. Поэтому дифференциал объёма
, который приближенно может быть принят за цилиндр с основанием S(x) и высотой dx. Поэтому дифференциал объёма  .
.
3) Находим искомую велечину V путём интегрирования dA в пределе отa до b:

88. Объем тела вращения.
Пусть криволинейная трапеция D c границей 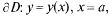
 вращается вокруг оси ОХ. Поперечными сечениями являются круги с радиусами у (х), поэтому
вращается вокруг оси ОХ. Поперечными сечениями являются круги с радиусами у (х), поэтому 
и 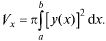
Пусть криволинейная трапеция D с границей  х = х(у),у=с, y=d(c<d),x = 0 вращается вокруг оси OY, тогда
х = х(у),у=с, y=d(c<d),x = 0 вращается вокруг оси OY, тогда 

89. Числовые ряды. Критерий Коши. Необходимое условие сходимости.
Числовым рядом называется выражение А 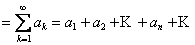 .
.
Наряду с {an}, рассмотрим последовательность частичных сумм {An} :
А1 = а1; А2 = а1+а2 = А1+а2; А3 = а1+а2+а3= А2+а3; …; 
Аn − nя частичная сумма ряда А .
Критерий Коши: Последовательность сходится тогда и только тогда , когда
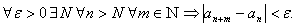 (не используется само значение предела!)
(не используется само значение предела!)
Теорема.Если ряд А сходится , то an →0 при n →∞ .
{ Пусть ряд А сходится и его сумма равна А. Рассмотрим an = An – An-1 и перейдем к пределу при
n→∞. Имеем:  }
}
90. Ряды с неотрицательными членами. Первый признак сравнения.
Для сходимости ряда  с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.
с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.
Признак сравнения рядов с неотрицательными членами.
Пусть даны два ряда  и
и 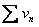 при un, vn 0.
при un, vn 0.
Теорема. Если un vn при любом n, то из сходимости ряда 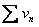 следует сходимость ряда
следует сходимость ряда  , а из расходимости ряда
, а из расходимости ряда  следует расходимость ряда
следует расходимость ряда
Доказательство. Обозначим через Sn и n частные суммы рядов  и
и 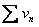 . Т.к. по условию теоремы ряд
. Т.к. по условию теоремы ряд 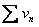 сходится, то его частные суммы ограничены, т.е. при всех n n M, где М – некоторое число. Но т.к. un vn, то Sn nто частные суммы ряда
сходится, то его частные суммы ограничены, т.е. при всех n n M, где М – некоторое число. Но т.к. un vn, то Sn nто частные суммы ряда  тоже ограничены, а этого достаточно для сходимости
тоже ограничены, а этого достаточно для сходимости
Теорема. Если  и существует предел
и существует предел  , где h – число, отличное от нуля, то ряды
, где h – число, отличное от нуля, то ряды  и
и 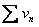 ведут одинаково в смысле сходимости
ведут одинаково в смысле сходимости
91. Признак сравнения в предельной форме.
Пусть неотрицательные функции f(x) и g(x) интегрируемы по любому отрезку [a, b] и пусть существует конечный  . Тогда несобственные интегралы
. Тогда несобственные интегралы  и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
 Док-во. Так как функции неотрицательны, то K > 0. По определению предела для
Док-во. Так как функции неотрицательны, то K > 0. По определению предела для  существует такое значение x0, что при x > x0 выполняется
существует такое значение x0, что при x > x0 выполняется 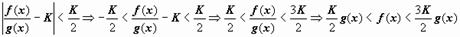 . Дальше рассуждения простые: пусть a1 = min{a, x0}; если сходится
. Дальше рассуждения простые: пусть a1 = min{a, x0}; если сходится  , то сходится
, то сходится  , тогда, по теореме сравнения, сходится
, тогда, по теореме сравнения, сходится 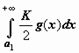
 сходится
сходится 
 сходится. Если расходится
сходится. Если расходится  , то расходится
, то расходится  , тогда, по теореме сравнения, расходится
, тогда, по теореме сравнения, расходится 
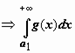 расходится
расходится 
 расходится. Случаи, когда сходится или расходится
расходится. Случаи, когда сходится или расходится  , рассмотреть самостоятельно.
, рассмотреть самостоятельно.
 Сравнение интеграла
Сравнение интеграла  со "стандартным" интегралом
со "стандартным" интегралом  в предельной форме позволяет сформулировать такое правило: если при
в предельной форме позволяет сформулировать такое правило: если при  неотрицательная функция f(x) - бесконечно малая порядка малости выше первого по сравнению с
неотрицательная функция f(x) - бесконечно малая порядка малости выше первого по сравнению с  , то
, то  сходится; если f(x) не является бесконечно малой или имеет порядок малости единица или ниже, то интеграл расходится
сходится; если f(x) не является бесконечно малой или имеет порядок малости единица или ниже, то интеграл расходится
92. Признак Даламбера. Признак Раабе.
Признак Д'Аламбера Если  то при q < 1 ряд
то при q < 1 ряд 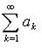 сходится, при q > 1 расходится.
сходится, при q > 1 расходится.
Признак Раабе Если  то при r > 1 ряд
то при r > 1 ряд  сходится, при r < 1расходится.
сходится, при r < 1расходится.
93. Признак Коши.
Если  (или
(или  ), то при
), то при  ряд
ряд  сходится, при q > 1 расходится.
сходится, при q > 1 расходится.
94. Интегральный признак Коши-Макларена.
признак сходимости убывающего положительногочислового ряда. Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на 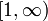 , последний часто может быть найден в явном виде.
, последний часто может быть найден в явном виде.
95. Доказать отсутствие универсального ряда сравнения.
96. Абсолютно и условно сходящиеся ряды. Теорема Римана. Теорема Коши.
97. Признак Дирихле.
Пусть:
1) функция f (x) интегрируема в любом конечном промежутке [а, А] (А > а), и интеграл  является ограниченным
является ограниченным
 ;
;
2) функция g( x) монотонно стремится к 0 при х → ∞
 ,
,
тогда интеграл 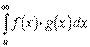 сходится.Так интегралы
сходится.Так интегралы 
при λ > 0 и а > 0 сходятся по признаку Дирихле, так как все условия этого признака выполнены:
 и
и  монотонно стремится к нулю при х→ ∞.
монотонно стремится к нулю при х→ ∞.
98. Признак Абеля.
функции f(x) и g(x) определены в промежутке [а, +∞), причём
функция f( x) интегрируема в этом промежутке, так что интеграл  сходится (хотя бы и неабсолютно),
сходится (хотя бы и неабсолютно),
функция g( x) монотонна и ограничена:  ,тогда интеграл
,тогда интеграл  сходится.
сходится.
Доказательство. Воспользуемся второй теоремой о среднем значении, при любых A' > A > a, будем иметь
 ,где А ≤ x ≤ А'. Так как интеграл
,где А ≤ x ≤ А'. Так как интеграл  сходится, то для произвольного как угодно малого ε > 0 найдётся такое число А0 > a, чтобы при А > A0 и А' > А0 выполнялись неравенства
сходится, то для произвольного как угодно малого ε > 0 найдётся такое число А0 > a, чтобы при А > A0 и А' > А0 выполнялись неравенства
 .
.
Далее из соотношения
 вытекает сходимость рассматриваемого интеграла
вытекает сходимость рассматриваемого интеграла
99. Признак Лейбница.
100. Арифметические операции над числовыми рядами.
Имея дело с суммой конечного числа слагаемых, можно менять слагаемые местами и расставлять скобки - от этого результат не изменится.
абсолютно сходящиеся ряды полностью копируют поведение суммы конечного числа слагаемых, а условно сходящиеся - нет.
Дата добавления: 2018-04-04; просмотров: 542; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
