Задачи анализа и моделирования временных рядов
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПОЛУЧЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ, АНАЛИЗА ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ С ПРИМЕНЕНИЕМ ПК
Задачи оптимизации в маркетинге и их решение на основе ППП Excel
Задача 1. Фирма освоила производство столов и тумбочек для торговой сети из древесины первого и второго видов. Всего имеется 72 м3 древесины первого вида и 56 м3 древесины второго вида. При этом на производство одного стола (одной тумбочки) требуется 0,18 (0,09) м3 древесины первого вида и 0,08 (0,28) м3 древесины второго вида. От производства одного стола мастерская получает прибыль в размере 1,1 д.е., а одной тумбочки – 0,7 д.е. Сколько столов и тумбочек должна изготовить фирма из имеющейся древесины, чтобы получить наибольшую прибыль?
Решение. Пусть х1, х2 - объемы производства столов и тумбочек.
Составим экономико-математическую модель данной задачи, включающей в себя целевую функцию (функцию цели или критерий оптимизации), ограничения по ресурсам и граничные условия.
Целевая функция – это математическая запись критерия оптимальности, т.е. выражение, которое необходимо максимизировать:
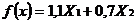 .
.
Ограничения по ресурсам и граничные условия имеют следующий вид:
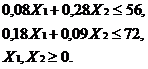
Приведем подробное описание технологии получения решения приведенной задачи линейного программирования (ЗЛП) с помощью пакета прикладных программ Excel.
Обозначим: М1 – один щелчок левой кнопкой мыши; М2 – двойной щелчок левой кнопкой мыши.
|
|
|
Далее необходимо последовательно выполнить следующий алгоритм.
10. Создать форму для ввода условий задачи. Запустить Excel, выбрав Microsoft Excel из подменю Программыглавного меню Windows. Открывается чистый лист Excel.
Создать текстовую форму – таблицу для ввода условий задачи (рис. 1).
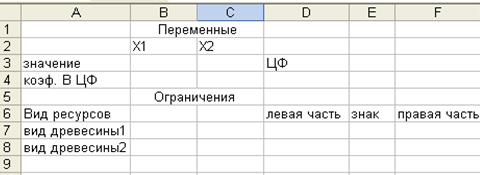
Рис.1 Текстовая форма для ввода условий ЗЛП
20. Указать адрес ячеек, в которые будет помещен результат решения (изменяемые ячейки). Обозначим через 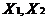 количество продукции каждого вида. В нашей задачи оптимальные значения компонент вектора
количество продукции каждого вида. В нашей задачи оптимальные значения компонент вектора 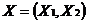 будут помещены в ячейках B3:C3, оптимальные значения целевой функции – в ячейке D4.
будут помещены в ячейках B3:C3, оптимальные значения целевой функции – в ячейке D4.
30. Ввести исходные данные задачи в таблицу (рис. 2). Сохранить таблицу.
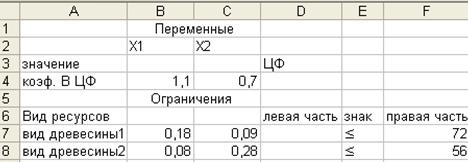
Рис. 2. Введение исходных данных задачи
40. Ввести зависимость для целевой функции:
· курсор в ячейку D4.
· курсор на кнопку «Мастер функций», расположенную на панели инструментов.
· М1. На экране появляется диалоговое окно Мастер функций – шаг 1 и 2(рис. 3).
· курсор в окно«Категории»на категорию Математические;
· М1;
· курсор в окно Функциина СУММПРОИЗВ;
· М1.На экране появляется диологовое окно СУММПРОИЗВ(рис. 4);
· в строку «Массив 1» ввести B$3:C$3;
· в строку «Массив 2» B4:C4;
· кнопка «ОК» на экране: в ячейку D4введена функция (рис. 4).
|
|
|
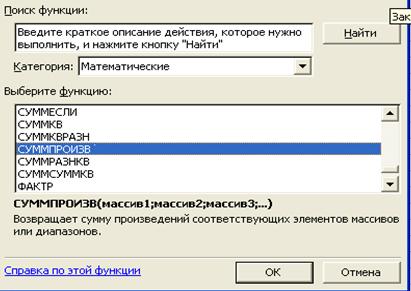
Рис. 3. Диалоговое окно
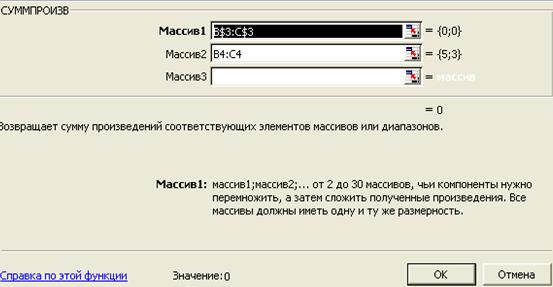
Рис. 4. Диалоговое окно
50. Ввести зависимости для ограничений (рис. 5):
· курсор в ячейку D4;
· щелчок правой кнопкой мыши ->Копировать -> М1;
· выделить ячейки D7 – D8;
· щелчок правой кнопкой мыши -> Вставить->М1;
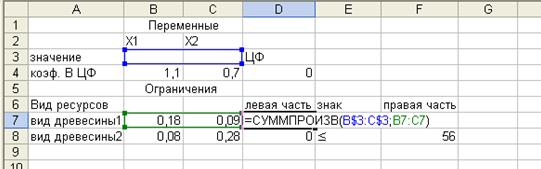
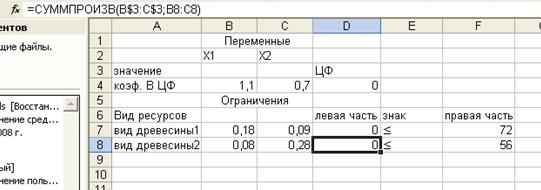
Рис. 5. Введение зависимостей для ограничений
В строке Меню указатель мыши на имя Сервис -> М1. в развернутом меню команда Поиск решения -> М1. Появляется диалоговое окно Solver Parameters (Поиск решения) (рис.6).
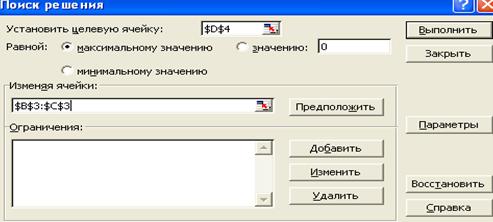
Рис. 6. Диалоговое окно
60. Назначить целевую функцию (установить целевую ячейку):
· курсор в строку Set Target Cell (Установить целевую ячейку);
· ввести адрес ячейки $D$4;
· ввести направление целевой функции в зависимости от условия задачи. В нашем случае – Max (Максимальному значению);
· курсор в строку By Changing Cells (Изменяя ячейки);
· ввести адреса искомых переменный B$3:C$3.
70. Ввести ограничения:
· указатель мышки на кнопку Add (Добавить) ->М1. Появляется диалоговое окно Add Constraint (Добавление ограничения)(рис. 7);
· в строке Cell Reference (Ссылка на ячейку)ввести адрес $D$7;
· ввести знак ограничения <=;
· в строке Constraint (Ограничение)ввести адрес $G$7;
· указатель мыши на кнопку Add (Добавить) -> М1.На экране вновь диалоговое окно Add Constraint (Добавление ограничения)(рис. 7).
|
|
|
· Ввести остальные ограничения задачи по вышеописанному алгоритму;
· после введения последнего ограничения кнопка ОК.
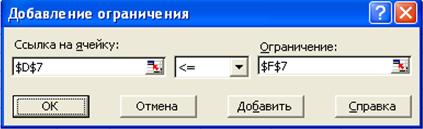
Рис. 7. Диалоговое окно
На экране появится диалоговое окно Solver Parameters (Поиск решения) с введенными условиями (рис. 8).
80. Ввести параметры для решения ЗЛП: в диалоговом окне указатель мыши на кнопку Options (Параметры). На экране появляется диалоговое окно Solver Options (Параметры поиска решения) (рис. 9);
- установить флажки в окнах Assume Linear Model (Линейная модель)(это обеспечивает применение симплекс-метода) и Assume Non-Negative (Неотрицательные значения);указатель мыши на кнопкуОК.
На экране диалоговое окноSolver Parameters (Поиск решения);
- указатель мыши на кнопку Solver (Выполнить).
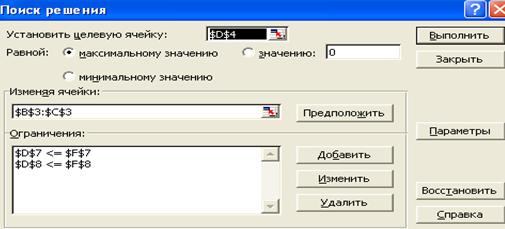
Рис. 8. Диалоговое окно
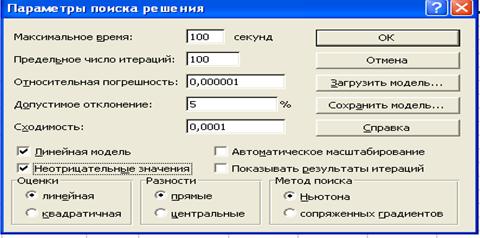
Рис. 9. Диалоговое окно
Спустя время появится диалоговое окно Solver Results (Результаты поиска решений) (рис. 10), таблица с заполненными ячейками В3:С3 для значений 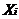 , ячейка D4с максимумом значения целевой функции (рис. 11).
, ячейка D4с максимумом значения целевой функции (рис. 11).
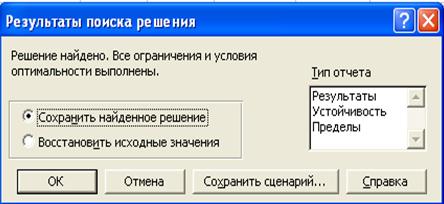
Рис. 10. Диалоговое окно
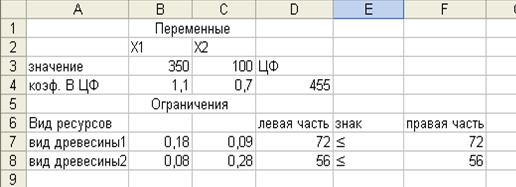
Рис. 11. Искомое решение ЗЛП
Полученное решение означает, что максимальную прибыль 445 д.е. фирма получит, если выпустит за месяц 350 изделий первого вида, 100 изделий второго вида.
|
|
|
Проверка решения: max f(x) = 1,1*350 + 0,7*100 = 385 + 70 = 455 д.е. Оптимальный план ЗЛП при этом Х = (х1 = 350; х2 = 100; х3 = 0; х4 = 0), т.е. все имеющиеся в запасе ресурсы использованы в производстве полностью.
Задача 2. Фирма производит два вида изделий А и Б, рынок сбыта которых не ограничен. Каждое изделие должно пройти обработку на каждой из трех машин 1, 2 и 3. Время обработки (в часах) для каждого изделия А на машинах 1, 2 и 3 составляет 0,5 ч, 0,4 ч и 0,2 ч соответственно, а для каждого из изделий Б время обработки на этих машинах равно соответственно 0,25 ч, 0,3 ч и 0,4 ч. Ресурсы времени работы машин 1, 2 и 3 типов составляют 40; 36 и 36 ч в неделю соответственно. Прибыль от изделий А и Б равна соответственно 5 и 3 д.е. за одно изделие. Определить недельный план выпуска изделий А и Б, обеспечивающий максимизацию прибыли.
Составим экономико-математическую модель. Обозначим через 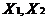 . объемы производства соответствующего вида продукции. Тогда имеем:
. объемы производства соответствующего вида продукции. Тогда имеем:
max 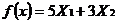 ; ограничения по ресурсам:
; ограничения по ресурсам: 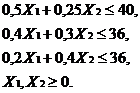
Решение. Подробное описание технологии получения решения приведенной ЗЛП дано выше, в задаче 1, поэтому приведем лишь результаты.
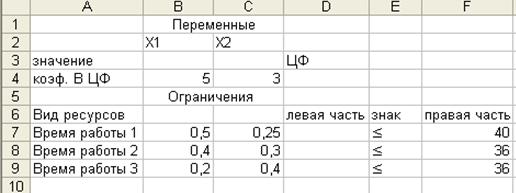
а)
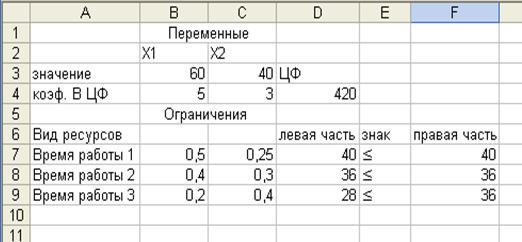
б)
Рис. 1. Начальная (а) и конечная (б) формы решения ЗЛП
Результат решения означает, что максимальную прибыль в 420 д.е. фирма получит, если выпустит за месяц 60 изделий первого вида и 40 изделий второго вида.
Задача 3. Из 505 м2 ткани нужно сшить не более 150 женских платьев не более 100 детских платьев. На пошив одного женского и детского платья требуется соответственно 3 м2 и 1 м2 ткани. При реализации каждого женского платья получают 10 д.е. прибыли, а детского - 5 д.е. Сколько нужно сшить женских и детских платьев, чтобы получить наибольшую прибыль?
Решение. Экономико-математическая модель имеет вид:
max f(x) = 10х1 + 5х2; ограничения 3х1 + х2 ≤ 505;
х1 ≤ 150;
х2 ≤ 100;
х1 ≥ 0, х2 ≥ 0.
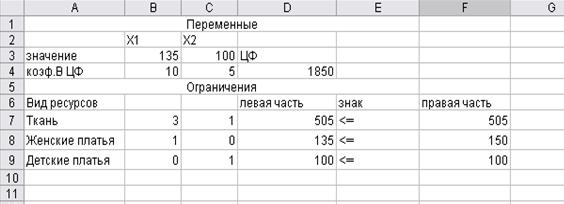
Рис. 1. Результат решения ЗЛП
Полученное решение означает, что максимальную прибыль 1850 д.е. фирма получит, если сошьет 135 женских и 100 детских платьев.
Задача 3. Можно закупить корм 1 и 2, при этом стоимость единиц корма вида 1 равна 2 ден. единицам, а вида 2 – 4 ден. единицы. В каждой единице корма 1 содержится одна единица витамина А, две единицы витамина В и нет витамина С, а в каждой единице корма 2 – две единицы А, одна В и одна единица С. Животному в сутки необходимо не менее 10 единиц витамина А, 10 единиц витамина В и 4 единицы витамина С. Составить наиболее дешевый рацион питания животного в расчете на сутки.
Экономико-математическая модель имеет вид:
Целевая функция - 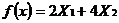 ;
;
Ограничения по ресурсам: 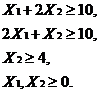
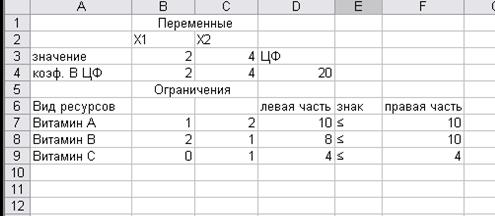
Рис. 1. Результат решения ЗЛП
Задача 4. Издательство «Геоцентр-Медиа» издает два журнала «Автомеханик» и «Инструмент», которые печатают в трех типографиях «Алмаз-Пресс», «Карелия-Принт» и «Hansaprint» (Финляндия). Время, отведенное для печати 1000 экземпляров, ограничено (табл. 1). Спрос на журнал «Инструменты» не превышает 7500 экземпляров, на журнал «Автомеханик» - 12000 экземпляров в месяц. Определить оптимальное количество журналов, обеспечивающее максимальную выручку от продажи.
Таблица 1. Исходные данные ЗЛП
| Типография | Время печати 1000 экземпляров | Ресурс времени, отведенный типографией, ч | |
| «Автомеханик» | «Инструмент» | ||
| Алмаз-Пресс | 2 | 14 | 112 |
| Карелия-Принт | 4 | 6 | 70 |
| Hansaprint | 6 | 4 | 80 |
| Оптовая цена, руб./шт. | 16 | 12 | |
Экономико-математическая модель данной задачи имеет вид:
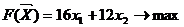 при ограничениях:
при ограничениях: 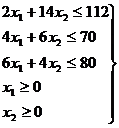 ;
; 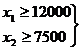
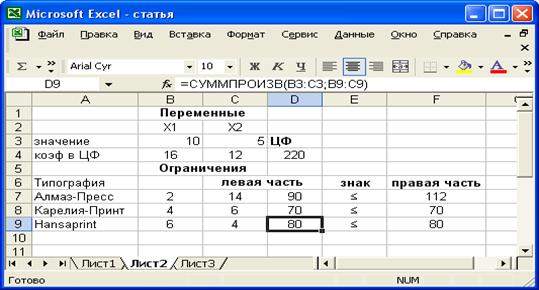
Рис. 1. Результат решения ЗЛП
Задачи анализа и моделирования временных рядов
Задача 1. На основании информации о деятельности фирмы в течение 9 лет (табл. 1) провести следующие действия с использованием ППП Excel:
- определить наличие тренда Yp(t);
- построить линейную модель Yp(t) = a0 + a1xt, параметры которой оценить по методу наименьших квадратов (МНК);
- построить точечный и интервальный прогнозы трудоемкости производства продукции на два года вперед.
Таблица 1. Сведения о деятельности фирмы
| Текущий номер года, t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Трудоемкость продукции, yt | 8,8 | 9,2 | 8,4 | 7,8 | 8,1 | 7,4 | 6,7 | 5,8 | 6 |
Решение. Для решения данной задачи выполним следующий алгоритм:
10. Определим наличие тренда по методу Тинтнера, для чего в столбцы А и В занесем исходные данные (рис. 1).
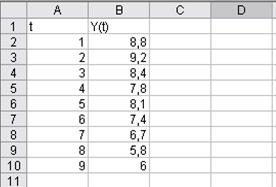
Рис.1. Окно - исходная таблица
20. Проверим гипотезу о равенстве дисперсий с помощью F-теста, который можно найти среди инструментов Анализа данных (рис. 2)
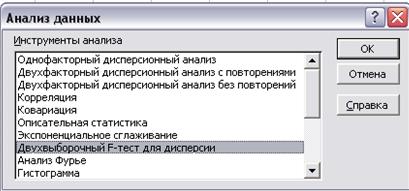
Рис. 2. Окно «Анализ данных»
30. Ввести данные для выполнения F-теста, указав интервал для первой и второй переменных (рис. 3). Результат выполнения теста приведен на рис. 4. Анализируя результаты выполнения двухвыборочного F-теста для проверки гипотезы о равенстве дисперсий, делаем вывод, что дисперсии различаются незначимо.
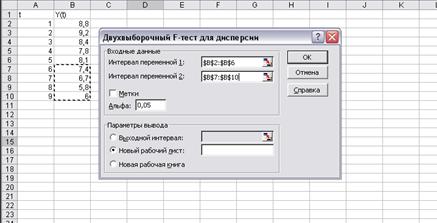
Рис. 3. Диалоговое окно
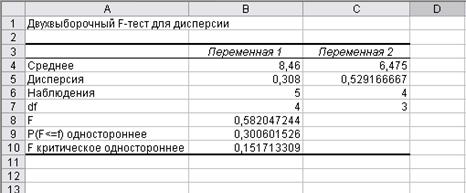
Рис. 4. Расчетные результаты анализа метода Тинтнера
40. Выбрать инструмент анализа Двухвыборочный t-тест с одинаковыми дисперсиями (рис. 5) и ввести данные (рис. 6). Результат выполнения t-теста дан на рис.7. Анализируя тест, видно, что тренд существует.
50. Построение линейной модели вида yt = a0 + a1t.
Определим параметры модели yt по методу МНК с помощью надстройки Анализ данных. Для регрессионного анализа необходимо:
- выбрать команду Сервис →Анализ данных.В окне Анализ данных выбрать инструмент Регрессия, а затем нажать кнопку ОК(рис.8);
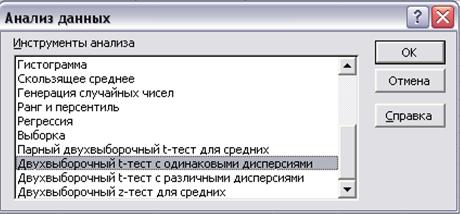
Рис. 5. Диалоговое окно
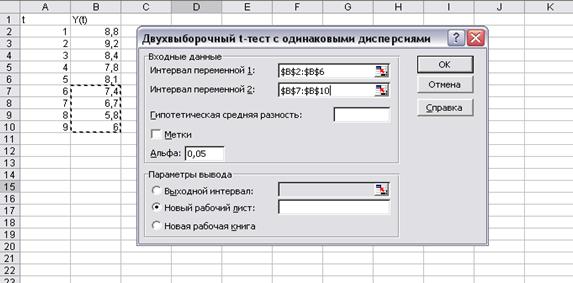
Рис.6. Диалоговое окно
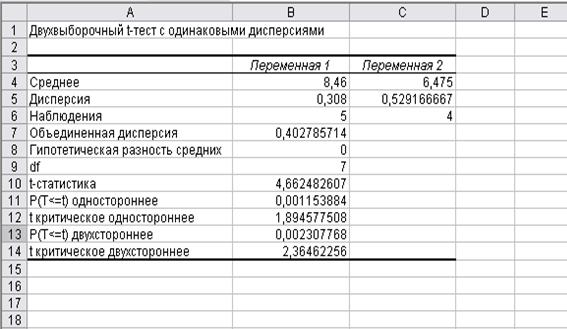
Рис. 7. Результаты теста
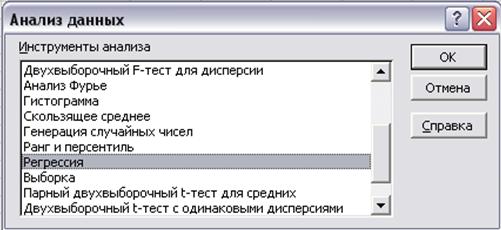
Рис. 8. Диалоговое окно
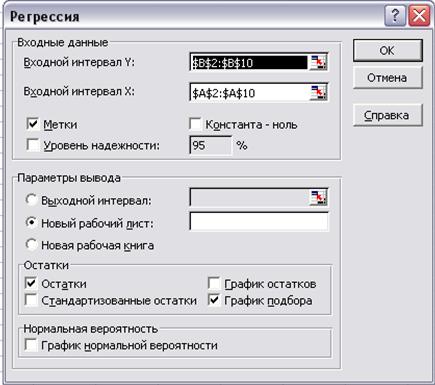
Рис. 9. Диалоговое окно
- в окне Регрессия в поле Входной интервал Y ввести адрес одного диапазона ячеек, который представляет зависимую переменную. В поле Входной интервал X ввести адрес диапазона, который содержит значения независимой переменной t. Если выделены и заголовки столбцов, установить флажок Метки в первой строке;
- выбрать параметры вывода (в данном примере – Новый рабочий лист); в поле График подбора поставить флажок; в поле Остаткипоставить необходимые флажки и нажать кнопу ОК (рис. 9).
Результат регрессионного анализа получим в виде, приведенном на рис. 10. Во втором столбце таблицы рис. 10 находятся коэффициенты уравнения регрессии а0 = 10,00476; а1.= -0,469047.
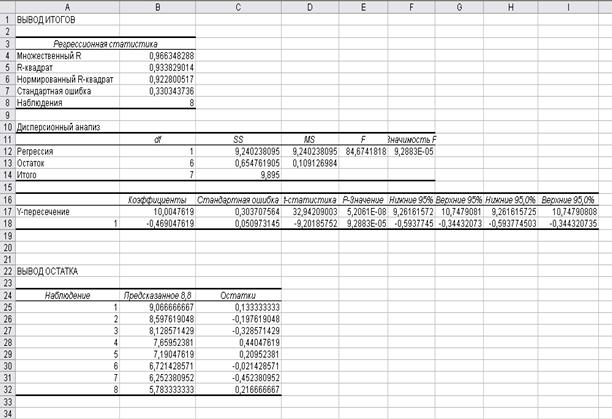
Рис. 10. Результат регрессионного анализа
Уравнение регрессии имеет следующий вид: Yt = 10 - 0,47t.
60. Проведем оценку параметров линейной модели вручную (рис. 11).
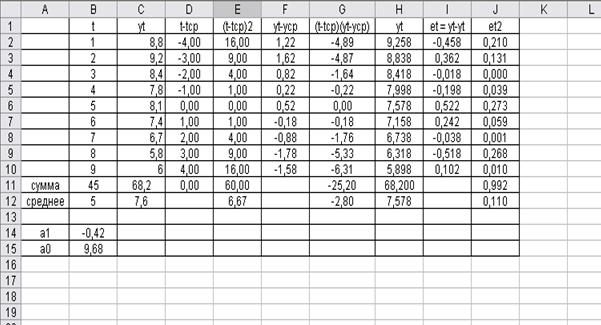
Рис. 11. Промежуточные расчеты данных линейной модели
В результате расчетов получаем примерно аналогичные результаты.
Иногда для проверки расчетов полезно проверить формулы. Для этого следует выбрать команду Сервис →Параметры и поставить флажок в окне формулы (рис. 12). После этого на листе Excel расчетные значения будут заменены соответствующими формулами и функциями (рис. 13).
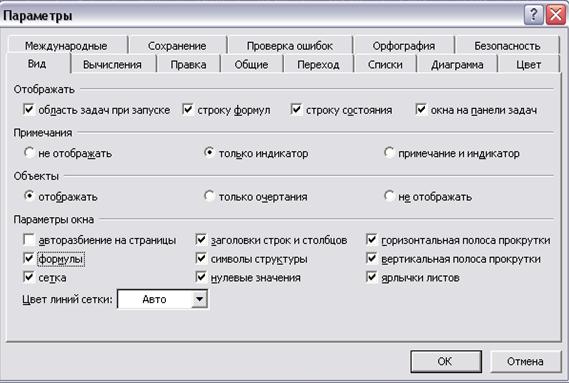
Рис. 12. Диалоговое окно
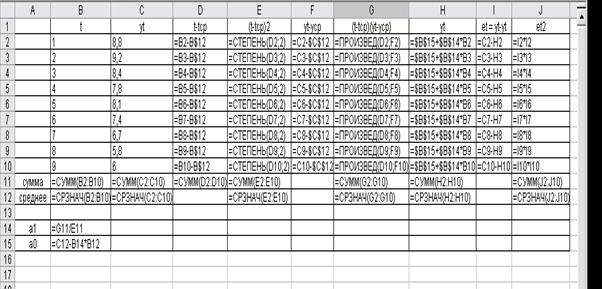
Рис. 13. Программа на Excel.
70. Построение точечного и интервального прогноза на 2 шага вперед.
Для вычисления точечного прогноза в построенную модель подставляем соответствующие значения фактора t = n + k: 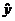 прогн(n+k) = а0 + а1(n+k). Тогда получим:
прогн(n+k) = а0 + а1(n+k). Тогда получим: 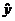 = 10 - 0,47*10 = 5,3;
= 10 - 0,47*10 = 5,3; 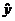 = 10 - 0,47*11 = 4,83.
= 10 - 0,47*11 = 4,83.
Для вычисления интервального прогноза рассчитаем доверительный интервал. Ширину доверительного интервала рассчитаем по формуле:
Yn+L 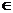
 (
( 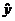 n+L -
n+L - 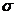 сКр;
сКр; 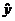 n+L +
n+L + 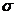 сКр),
сКр),
где 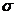 с возьмем из полученного протокола регрессионного анализа.
с возьмем из полученного протокола регрессионного анализа.
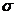 с =
с = 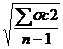 =
= 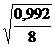 =
= 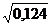 = 0,35.
= 0,35.
Таким образом, интервал равен: 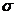 сКр = 0,35*1,05 = 0,3675.
сКр = 0,35*1,05 = 0,3675.
Далее вычислим верхнюю и нижнюю границы прогноза:
y10 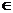 (5,3 – 0,3675 = 4,9325; 5,3 + 0,3675 = 5,6675),
(5,3 – 0,3675 = 4,9325; 5,3 + 0,3675 = 5,6675),
y11 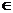 (4,83 – 0,3675 = 4,4625; 4,83 + 0,3675 = 5,1975).
(4,83 – 0,3675 = 4,4625; 4,83 + 0,3675 = 5,1975).
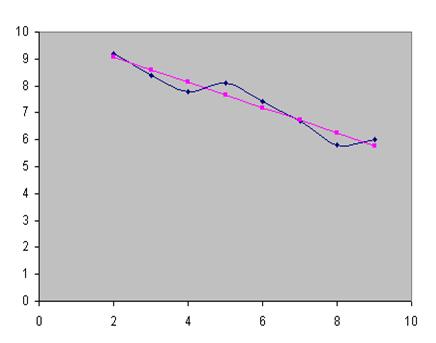
Рис. 14. График фактического временного ряда и его линейной модели
Дата добавления: 2018-04-05; просмотров: 243; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
