ЗАДАНИЕ 4. Анализ результатов моделирования и идентификации динамических характеристик
Управляемость линейных стационарных систем
Непрерывная линейная система
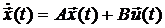
является полностью управляемой тогда и только тогда, когда она может быть переведена из любого начального состояния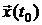 
в произвольный момент времени 
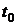в любое конечное состояние 
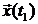за конечное время 
.
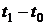Примем начальные условия нулевыми: 
. Тогда, в соответствии с формулой Коши
.
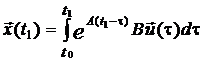Принимая во внимание выражение для матричной экспоненты в виде бесконечного ряда
,
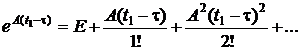равенство можно записать в виде
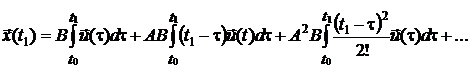
Обозначим:
.
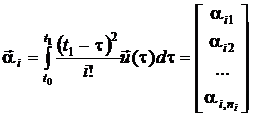Представим произведения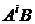 
в виде блочных матриц векторов 
: 
.
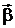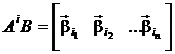Тогда
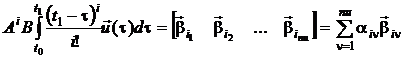
и
.
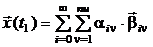В результате вектор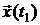 
может рассматриваться как линейная комбинация векторов 
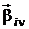, являющихся вектор-столбцами матриц 
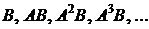. Иначе говоря, конечное состояние 
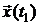принадлежит линейному подпространству, порождаемому вектор-столбцами бесконечной последовательностью матриц .
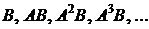В этой последовательности должна появиться матрица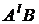 
, все вектор-столбцы которой линейно зависят от вектор-столбцов предыдущих матриц 
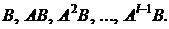Такая матрица обязательно должна иметь место, так как в линейном n-мерном пространстве не может быть более чем 
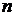линейно–независимых векторов. Отсюда же следует, что 
.
|
|
|
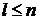Таким образом, можно записать
,
где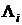 
- соответствующие диагональные матричные коэффициенты
.
Очевидно, тем же свойством обладает и матрица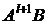 
, так как
.
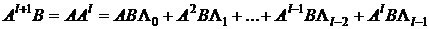По индукции можно утверждать то же самое и для всех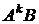 
при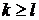 
.
Итак, конечное состояние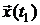 
принадлежит линейному подпространству, порождаемому вектор-столбцами матриц
... , 
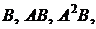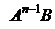
(здесь учтено, что 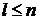). Если эти вектор-столбцы не порождают 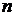-мерное пространство, то в такой системе можно достичь лишь тех состояний, которые принадлежат подпространству меньшей размерности.
Таким образом, критерий управляемости формулируется следующим образом:
Система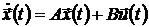 
полностью управляема тогда и только тогда, когда ранг матрицы управляемости
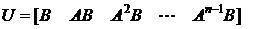
равен 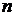, то есть полной размерности линейного пространства. При этом говорят, что пара матриц {A, B} полностью управляема.
|
|
|
Наблюдаемость линейных стационарных систем
В теории автоматического управления большую роль играет задача восстановления вектора состояния по результатам наблюдения за входом и выходом объекта.
Непрерывная система
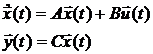
называется наблюдаемой, если вектор состояния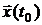 
можно определить, зная 
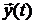на некотором интервале времени 
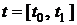. Если это справедливо для любого 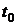, то система называется полностью наблюдаемой. Задачей настоящего параграфа является вывод критерия наблюдаемости.
Достаточно рассмотреть задачу при 
. Тогда
.
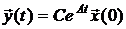В развёрнутом виде - это система алгебраических уравнений
,
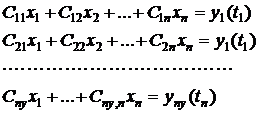в качестве неизвестных в которой выступают координаты вектора состояния. В связи с тем, что, как правило,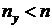 
, число уравнений оказывается меньше числа неизвестных, и решение невозможно.
В соответствии с теоремой Кэли-Гамильтона каждая квадратная матрица удовлетворяет собственному характеристическому уравнению:
|
|
|
.
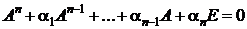Поэтому матричная экспонента, являющаяся степенным рядом относительно матрицы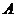 
, может быть представлена в виде полинома степени 
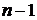. С учетом этого равенство можно записать в виде:
,
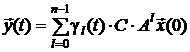где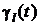 
– соответствующие коэффициенты этого полинома. Для i-й составляющей вектора выхода соответственно будем иметь
.
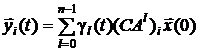Здесь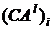 
– 
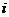-я строка матрицы 
.
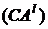Если набор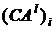 
для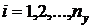 
; 
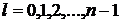не содержит полного базиса, то есть 
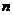линейно независимых строк, иначе говоря, если матрица
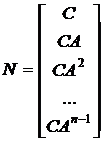имеет ранг, меньший, чем 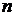, то в качестве ненулевого вектора начальных условий 
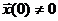может быть выбран вектор, ортогональный всем строкам матрицы N. Тогда в соответствии с получим, что 
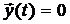для всех 
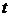, т.е. система не наблюдаема.
Теперь докажем, что если ранг матрицы N равен 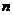, то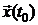 
может быть определен с помощью конечного числа измерений вектора выхода 
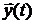. Обозначим
|
|
|
,
где Е – квадратная единичная матрица размером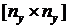 
. Моменты измерения 
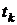выберем таким образом, чтобы для различных значений 
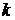элементы 
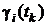отличались друг от друга. С учетом введенного обозначения равенство примет вид
.
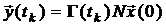Известно, что ранг произведения любых двух матриц не превосходит ранга каждого из сомножителей. Ранг матрицы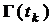 
не превосходит числа ее строк 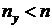. Проводя многократные измерения на интервале времени переходного процесса системы, построим расширенный вектор выхода
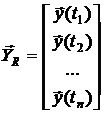
и обозначим
.
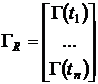Матрица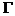 
имеет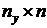 
строк. Моменты измерений должны быть выбраны таким образом, чтобы выполнялось условие 
. Как было обусловлено, ранг матрицы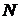 
также равен 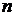. Поэтому уравнение
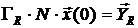
содержит 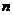линейно независимых скалярных уравнений, то есть оно может быть разрешено относительно вектора 
.
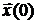Таким образом, доказан следующий критерий полной наблюдаемости стационарных линейных систем:
Линейная стационарная система вполне наблюдаема тогда и только тогда, когда ранг матрицы наблюдаемости N равен .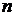
Для анализа результатов моделирования необходимо перевести полученные модели в модель в виде переменных состояния.
Дата добавления: 2018-04-05; просмотров: 175; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!