Оценка значимости параметрического коэффициента корреляции
Основы корреляционного анализа.
Наиболее простой вид связи между переменными величинами -- это функциональная зависимость:y=f(x). Каждому значению x соответствует одно значение y.
В медицине и биологии чаще встречается более сложный вид зависимости, когда каждому x соответствует множество значений y -- это корреляционная зависимость.
| x1 x2 x3 xn X |
| Y yn y3 y2 y1 |
| . y̅₁ |
| . y̅₂ |
| . y̅₃ |
| . y̅n |
| x̅1 |
| x̅2 |
| x̅3 |
| x̅n |
| x̅,y̅ |
| x=x̅(y) |
| y=y̅() |
То есть имеем целое «облако» из точек в системе координат. Каждому значению xi соответствуем множество значений y, среднее арифметическое этих значений y̅i называется условным средним.
Таким образом, среди множества точек с изменением xможно выделить точки, соответствующие условным средним y: y̅₁, y̅₂, y̅₃,….y̅n. Если соединить эти точки кривой линией, то получим линию регрессии, а соответствующая ей функция y=y̅(x) -- функция регрессии.
Точно также, при изменении значений y, каждому yiсоответствует множество значений x, их средние арифметические x̅i -- условные средние, соединив их кривой , получаем вторую линию регрессии, ей соответствует функция регрессии: x=x̅(y).
x̅,y̅ -- общие средние. Это средние арифметические, вычисленные по всем значениям x и y.
|
|
|
Следовательно, в отличии от функциональной зависимости, корреляционная зависимость характеризуется двумя линиями регрессии:
уравнение регрессии.
В настоящее время изучение различных корреляций является важным разделом многих биологических дисциплин, поэтому возникает потребность в количественном измерении корреляции. Для этого служит ряд методов, наиболее распространённым из которых является вычисление коэффициента корреляции -- это количественная характеристика связи (зависимости) между исследуемыми величинами.
Дисперсия суммы случайных величин. Корреляционный момент.
Xи Y -- случайные величины.
(1) Z=X+Y -- их сумма.
(2) M[Z]=M[X]+M[Y]
Найдём D[Z]=D[X+Y] , для этого вычтем из уравнения (1) уравнение (2):
(3) Z-M[Z]=X+Y-M[X]-M[Y]=(X-M[X])-(Y-M[Y])
Для сокращения записи обозначают:
Z-M[Z]=ΔZ
X-M[X]=ΔX Эти величины называют моментами.
Y-M[Y]=ΔY
Момент -- это отклонение каждого значения случайной величины от её математического ожидания.
Возведём уравнение (3) в квадрат: (Z-M[Z])2=((X-M[X])+(Y-M[Y]))2
ΔZ2=(ΔX+ΔY)2 , тогда
ΔZ2=ΔX2+ΔY2+2·ΔX·ΔY -- это сумма квадратов отклонений.
Математическое ожидание от суммы квадратов отклонений это дисперсия:
|
|
|
D[Z]=D[X+Y]=M[ΔZ2]=M[ΔX2]+M[ΔY2]+2·M[ΔX·ΔY]=D[X]+D[Y]+2·M[ΔX·ΔY]
Принято обозначение: M[ΔX·ΔY]=K[X,Y] -- корреляционный момент.
Основное свойства корреляционного момента: если величины Xи Y независимы, то их корреляционный момент K[X,Y]=0. Обратное утверждение неверно.
Из последнего утверждения следует:
Теорема сложения дисперсий.
Если величины Xи Y независимы, то:
D[X+Y]= D[X]+D[Y]
Этой теоремой пользуются в теории погрешностей, при обработке результатов косвенных измерений. Так как входящие в расчётные формулы величины в большинстве случаев независимы, то подсчитывая среднюю квадратическую погрешность, суммируют квадраты всех их погрешностей.
Коэффициент корреляции (параметрический).
Корреляционный момент K[X,Y] – размерная величина, то есть зависит от выбора единицы измерения. Это затрудняет сравнение корреляционных моментов различных случайных величин, поэтому удобнее использовать безразмерную величину -- коэффициент корреляции:
-- это коэффициент корреляции для генеральной совокупности.
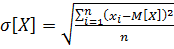
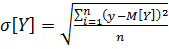-- средние квадратические отклонения при n→∞
Но мы имеем дело с выборкой, n конечно, выборочные оценки M[X] и M[Y] -- это x̅ и y̅ -- общие средние (средние арифметические всех значений X и Y, которые мы имеем из выборки).
|
|
|
Поэтому для вычисления коэффициента корреляции для выборки, используют формулу:
Свойства коэффициента корреляции:
1). -1≤R[X,Y]≤+1
если R[X,Y]˃0 то корреляция называется положительной,
если R[X,Y]<0 то корреляция называется отрицательной.
2). если R[X,Y]≈1, зависимость между X и Y близка к линейной.
3). 
, то X и Yсвязаны линейной зависимостью:
y=ax+b
x=cx+d
Так как мы имеем дело с выборочной совокупностью, то имеем не множество значений X и Y, а несколько пар выборочных значений: (xi,yi), i=1 : n.
| x1 x2 xn |
| yn y2 y1 |
| R≈+1 Например: X -- нагрузка ↑ Y -- частота пульса ↑ |
| Сильная положительная корреляция: |
| x1 x2 xn |
| yn y2 y1 |
| R≠+1, R˃0 Например: X -- число пятен на солнце ↑ Y – количество инфарктов ↑ |
| Слабая положительная корреляция: |
| Сильная отрицательная корреляция: |
| x1 x2 xn |
| y1 y2 yn |
| R≈-1 X↑, Y↓ |
| Корреляции (зависимости) нет. |
| x1 x2 xn |
| yn y1 y2 |
| R=0 |
|
|
|
Так как коэффициент корреляции R[X,Y] вычисляется по выборке, то есть является статистической оценкой ρ[X,Y]-- коэффициента корреляции генеральной совокупности, то R[X,Y] вычислен с ошибкой. Встаёт вопрос: достоверно ли значение выборочного коэффициента корреляции?
Оценка значимости параметрического коэффициента корреляции.
Проверка коэффициента корреляции на достоверность осуществляется по критерию Стьюдента.
Н0: ρ=0,следовательно R[X,Y] не достоверен (то есть коэффициент корреляции генеральной совокупности ρ=0, следовательно зависимости между XиY нет).
где σR -- ошибка выборочного коэффициента корреляции R[X,Y]
для n<30 
где n-2 число степеней свободы.
В таблице критерия Стьюдента по заданному уровню значимости α и числу степеней свободы: n-2 находим 
.
если 
Н0 принимаем. Вывод: R недостоверен, за висимости между XиY нет.
если 
Н0 отвергаем. Вывод: R достоверен, зависимость (корреляция) между XиY есть.
Если коэффициент корреляции достоверен, то можно переходить к построению линий регрессии и записать уравнение регрессии.
Построение линий регрессии.
Коэффициент корреляции R[X,Y] указывает лишь на наличие связи двух величин, но не даёт возможности судить, как количественно изменяется одна величина относительно другой. Ответ на этот вопрос даёт регрессионный анализ.
Корреляционная зависимость характеризуется двумя линиями регрессии:
| ┐α |
| a |
| y=y̅(x) |
| x=x̅(y) |
| x1 x2 x̅ |
| y̅ y2 y1 |
| x̅,y̅ общие средние. |
b=tg α -- угловой коэффициент.
Если R[X,Y] ≠1,то условные средние y̅I не лягут на одну прямую, но при R[X,Y] ≈1 (R=0,95, R=0,85) можно провести усредняющую прямую. Так как имеем две линии регрессии:
то для y=y̅(x):
то для x=x̅(y):
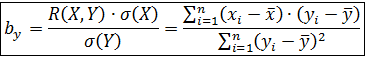
σ(Y)=Sn(Y) выборочные оценки среднего
σ(X)=Sn(X) квадратического отклонения.
Так как обе линии регрессии проходят через точку с координатами (x̅,y̅), где x̅,y̅ -- общие средние, вычисленные по выборке, то уравнение регрессии имеет вид:
или:
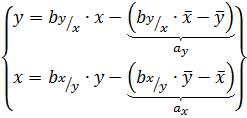
6. Ранговый коэффициент корреляции.
Определить, есть ли связь между признаками XиY, можно и с помощью рангового коэффициента корреляции. Он менее точен и не может использоваться для построения линий регрессии, но так как ранговый коэффициент корреляции легко вычислить, есть смысл воспользоваться им для первоначальной оценки связи между признаками.
Ранговый коэффициент корреляции вычисляется по формуле:
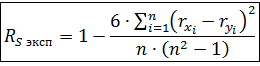
n -- число пар x,y (объём выборки).
rxi -- ранг по признаку X
ryi -- ранг по признаку Y.
То есть ранги отдельно расставляются для XиY.
Так как RS эксп вычислен по выборке, то он также нуждается в проверке на достоверность.
Для этого RS эксп сравнивают с RS критич , найденным в таблице ранговой корреляции ,для заданного уровня значимости α и числа степеней свободы n-2.
Н0: RS эксп не достоверен.
Если |RS эксп| < RS критич то RS ,полученный по выборке не достоверен, корреляции (зависимости) между XиY нет.
Если |RS эксп| ˃ RS критич то RS ,полученный по выборке достоверен, корреляция (зависимость) между XиY есть.
Пример: По критерию ранговой корреляции выяснить, есть ли корреляция между признаками XиY для уровня значимости α=0,05.
| X | Y | rxi | ryi | (rxi-ryi) | (rxi-ryi)2 |
| 23 | 5 | 4 | 5 | -1 | 1 |
| 21 | 1 | 3 | 1 | 2 | 4 |
| 24 | 4 | 5 | 4 | 1 | 1 |
| 20 | 3 | 1,5 | 3 | -1,5 | 2,25 |
| 28 | 8 | 9,5 | 8 | 1,5 | 2,25 |
| 20 | 2 | 1,5 | 2 | 0,5 | 0,25 |
| 26 | 7 | 7 | 7 | 0 | 0 |
| 25 | 6 | 6 | 6 | 0 | 0 |
| 27 | 10 | 8 | 10 | -2 | 4 |
| 28 | 9 | 9,5 | 9 | 0,5 | 0,25 |
| Σ=15 |
n=10
α=0,05
Н0: RS эксп не достоверен, корреляции нет.
По таблице ранговой корреляции для α=0,05 и числа степеней свободы 10-2=8 находим: RS критич=0,64.
Так как 
Н0 отвергаем.
Вывод: Ранговый коэффициент корреляции достоверен, корреляция между признаками XиY есть.
Вычислим параметрический коэффициент корреляции:
| X | Y | xi-x̅ | yi-y̅ | (xi-x̅)(yi-y̅) | (xi-x̅)2 | (yi-y̅)2 |
| 23 | 5 | -1,2 | -0,5 | 0,6 | 1,44 | 0,25 |
| 21 | 1 | -3,2 | -4,5 | 14,4 | 10,24 | 20,25 |
| 24 | 4 | -0,2 | -1,5 | 0,3 | 0,04 | 2,25 |
| 20 | 3 | -4,2 | -2,5 | 10,5 | 17,64 | 6,25 |
| 28 | 8 | 3,8 | 2,5 | 9,5 | 14,44 | 6,25 |
| 20 | 2 | -4,2 | -3,5 | 14,7 | 17,64 | 12,25 |
| 26 | 7 | 1,8 | 1,5 | 2,7 | 3,24 | 2,25 |
| 25 | 6 | 0,8 | 0,5 | 0,4 | 0,64 | 0,25 |
| 27 | 10 | 2,8 | 4,5 | 12,6 | 7,84 | 20,25 |
| 28 | 9 | 3,8 | 3,5 | 13,3 | 14,44 | 12,25 |
| x̅=24,2 | y̅=5,5 | Σ=79 | Σ=87,6 | Σ=82,5 | ||
| √∑̅=9,36 | √∑̅=9,08 |
Проверка на достоверность:
Н0: ρ=0,следовательно R[X,Y] не достоверен (то есть коэффициент корреляции генеральной совокупности ρ=0, следовательно зависимости между XиY нет).
В таблице критерия Стьюдента по заданному уровню значимости α=0,05 и числу степеней свободы: n-2=10-2=8 находим =2,31
Так как Н0 отвергаем. Вывод: R достоверен, зави
симость (корреляция) между XиY есть.
Построение линий регрессии:
Уравнение регрессии:
| x=0,96y+18,9 |
| y=0,9x-16,3 |
| (x̅,y̅) |
Контрольные вопросы.
Что такое корреляция?
2. Дисперсия суммы случайных величин. Корреляционный момент.
Теорема сложения дисперсий.
Дата добавления: 2018-04-05; просмотров: 733; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!