Теорема Котельникова. Вводная информация
Если fmax – самый высокочастотный компонент сигнала, то, чтобы элементы выборки полностью описывали сигнал, дискретизация сигнала должна осуществляться с частотой не ниже 2 fmax:
Fs > 2 fmax, (6)
где Fs – частота дискретизации. Следовательно, если максимальная частота аналогового сигнала составляет 4 кГц, то для того, чтобы собрать или сохранить всю информацию, содержащуюся в сигнале, его дискретизация должна осуществляться с частотой 8 кГц или больше. Дискретизация с частотой, меньшей той, которую дает теорема о дискретном представлении, приведет к появлению перегибов или наложению зеркальных частот в интересующей нас частотной области. Следовательно, если захочется преобразовать дискретную информацию обратно в аналоговую, исходный сигнал будет уже невозможно восстановить. Важно помнить о том, что часто значительная доля энергии сигнала может попадать за пределы интересующей нас частотной области, и/или сигнал может содержать шум, ширина полосы которого всегда будет большой. Например, в телефонной связи самая высокая из представляющих интерес частот составляет приблизительно 3,4 кГц, но частоты речевого сигнала могут превышать 10 кГц. Поэтому, если не удалить лишний сигнал или шум за пределы полосы интересующих нас частот, теорема о дискретном представлении выполняться не будет. На практике это достигается путем предварительного пропускания сигнала через аналоговый фильтр защиты от наложения спектров.
|
|
|
Наложение и спектры дискретных сигналов
Предположим, мы выполнили дискретизацию сигнала в определенной временной области с интервалом T (в секундах) (т.е. частота дискретизации равна 1/T (в герцах)). Видно (рис. 44), что в исходном сигнале есть еще одна частотная составляющая с таким же набором дискретных значений. Следовательно, этот частотный компонент можно ошибочно принять за компонент с более низкой частотой. Это и есть наложение. С точки зрения анализа следствий или поиска решения задачи наложения исследовать наложение лучше в частотных координатах.
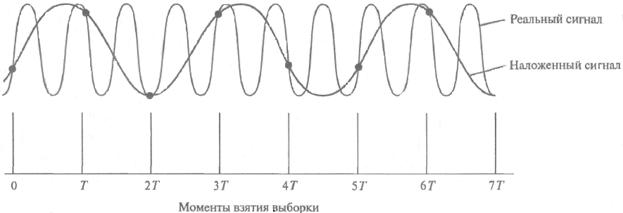
Рис. 44. Пример наложения во временных координатах. Обратите внимание на то, что оба сигнала имеют одинаковые значения в одних и тех же точках, хотя их частоты различны
На рис. 45 показан процесс дискретизации, который можно рассматривать как умножение аналогового сигнала x(t) на выборочную функцию p(t). Функция p(t) состоит из импульсов единичной амплитуды с шириной dt (бесконечно малой величиной) и периодом Т. Спектр сигнала x(t), функция p(t) и их произведение показаны на рис. 2.5. Заметим, что X'(f) – это свертка X(f) и P(f), следовательно, умножение во временных координатах эквивалентно свертке в частотных координатах.
|
|
|
Для дискретного сигнала (рис. 45, г) следует отметить такие моменты:
- Спектр идентичен исходному аналоговому спектру, только повторяется в точках, кратных частоте дискретизации Fs. Компоненты более высокого порядка с центрами в точках, кратных Fs, называются зеркальными частотами.
- Если частота дискретизации Fs недостаточно высока, то зеркальные частоты с центром в Fs будут, например, накладываться на частоты основной полосы. В этом случае полезную информацию, содержащуюся в сигнале, невозможно отличить от его образа в области наложения.
- Перекрывание (или наложение) происходит в районе точки FN, равной половине частоты дискретизации. Эту точку часто называют максимальной частотой сигнала, частотой Найквиста, частотой Котельникова и т.п.
На практике наложение существует всегда, из-за шума и наличия энергии сигнала за пределами полосы частот, которая представляет интерес. Поэтому задача разработчика – определить уровень допустимого наложения, создать подходящий фильтр защиты от наложения спектров и выбрать подходящую для этого частоту дискретизации.
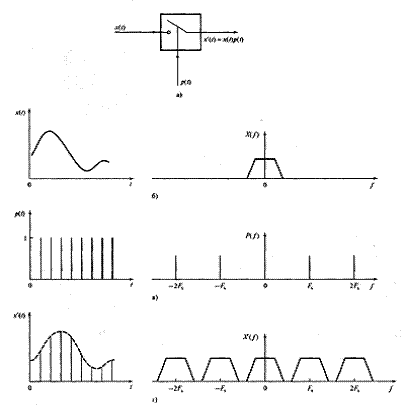
Рис. 45. Описание процесса дискретизации во временной и частотной областях. Сравните спектры сигнала
до (б) и после (г) дискретизации. Обратите внимание на изменения в дискретном сигнале и, в частности,
на то, что спектр дискретного сигнала повторяется в точках, кратных частоте дискретизации Fs
Дата добавления: 2018-04-05; просмотров: 1161; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
